基于逆向搜索的模糊Petri網分層算法
向寅鴻,周愷卿,楊森宇,張軒宇,康棣文
基于逆向搜索的模糊Petri網分層算法
向寅鴻,周愷卿*,楊森宇,張軒宇,康棣文
(吉首大學 通信與電子工程學院,湖南 吉首 416000)(?通信作者電子郵箱kqzhou@jsu.edu.cn)
模糊Petri網(FPN)是知識庫系統(KBS)表示、建模與分析的主要工具之一。針對部分FPN層次結構不清晰、庫所/變遷間從屬關系不明確的問題,提出一種基于逆向搜索的FPN分層算法(HFPN-RS)以實現非層次化FPN到層次化FPN(HFPN)的自動轉換。首先,從終結庫所開始對整個FPN進行逆向搜索,將所有輸入庫所的前集、輸出庫所的后集分別劃分在同一層;其次,通過添加虛庫所-虛變遷對的方式明確整個模型的層次結構;同時提出兩條相關定理以明確HFPN分層層數的下確界和層次化操作中需要添加的最少虛庫所-虛變遷對數,并給出經層次化操作后具有完整分層結構的FPN模型關聯矩陣維度計算公式。在實驗部分,通過對幾類各具特點的FPN模型進行層次化操作,并利用所提定理進行驗證。實驗結果表明,添加虛庫所-虛變遷對后新FPN模型具有清晰的層次結構,為下一步FPN泛化能力等研究內容的深入提供了理論基礎。
模糊Petri網;層次化;逆向搜索;虛庫所-虛變遷對;關聯矩陣
0 引言
模糊Petri網(Fuzzy Petri Net, FPN)是一類向后拓展的高級Petri網(Petri Net, PN)拓撲結構,它在繼承PN描述異步并發和圖形表示能力的基礎上,還具有對知識庫系統(Knowledge Based System, KBS)或專家系統(Expert System, ES)建模與執行模糊推理的能力[1-3]。目前,FPN被廣泛應用于生物系統[4-5]、能源系統[6-7]、制造業系統[8-9]和交通控制系統[10-11]等領域,但FPN仍存在部分參數難以精確獲得、泛化能力弱等不足[1]。針對這一問題,圍繞FPN自適應能力的泛化展開了一系列研究:文獻[12-13]中結合FPN與神經網絡,系統地研究了一類動態自適應FPN(Adaptive FPN, AFPN),并應用于表示動態知識,使得FPN模型初步具備了自適應能力;文獻[14]中將改進的遺傳粒子群算法應用于模糊知識動態表示(Dynamic Representation of Fuzzy Knowledge, DRFK)模型,一定程度上增強了FPN自學習能力;文獻[15]中提出一種結合直覺模糊抑制弧PN(Intuitionistic Fuzzy Inhibitor Arc PN, IFIAPN)和誤差反向傳播算法的電網故障診斷方法,利用BP(Back Propagation)神經網絡算法訓練模型的權重參數,提高推理精度;文獻[16]中提出了一種加權模糊神經PN(Weighted Fuzzy Neural PN,WFNPN),并應用于微電網的故障診斷,緩解了FPN對人工經驗的過度依賴,提高了泛化能力;文獻[17]中提出了一種基于PN、模糊理論和神經網絡算法的神經FPN(Neural FPN, NFPN),并應用于電機故障診斷;文獻[18]中設計了一種遞歸小波Petri模糊神經網絡(Recurrent Wavelet Petri Fuzzy Neural Network, RWPFNN)控制器,用于快速響應控制電網事故,減小故障對電網的影響。
由上述文獻可知,將FPN神經網絡化后,采用相應優化算法優化參數,提高FPN的自適應能力,以提高推理精度是FPN的研究熱點之一。作為一類有向二分圖,FPN可將庫所分為輸入庫所集、中間庫所集和輸出庫所集這3類,該結構天然對應神經網絡固有的輸入層、隱藏層、輸出層這3層結構[19]。FPN的這一結構特點為FPN模型神經網絡結構化提供了可能,為充分利用神經網絡的相關成果拓展FPN的應用領域奠定了基礎。
與神經網絡模型相比,FPN中的庫所/變遷存在嵌套使用情況,使FPN結構層次不清晰、庫所/變遷間從屬關系不明確,導致FPN的類神經網絡層次化操作難以自動實現;因此如果將神經網絡的相關研究成果充分運用于FPN模型,則需要對FPN模型進行層次劃分,從而明確庫所/變遷間的從屬關系。文獻[20]中提出的分層算法對部分情形考慮欠缺,如具有多輸入/多輸出庫所結構的FPN模型,無法得到清晰的層次結構等。為解決這一問題,本文針對無環結構的FPN模型提出了一種基于逆向搜索的FPN分層算法(Hierarchical algorithm of FPN by Reverse Search, HFPN-RS)。本文算法首先從終結庫所開始對整個FPN逆向搜索,利用前后集、可達集和直接可達集等概念,將所有輸入庫所的后集、輸出庫所的前集分別劃分在同一層;其次通過添加虛庫所-虛變遷對明確整個模型的層次結構;同時,本文提出相關定理明確了層次化FPN(Hierarchical FPN, HFPN)的分層層數的下確界和層次化操作中需添加的最少虛庫所-虛變遷對數,并給出了經層次化操作后具有完整分層結構的FPN模型關聯矩陣維度計算公式;最后,對提出的分層算法編程實現,通過相關案例,分別從實驗結果和理論驗證兩方面驗證HFPN-RS的正確性和魯棒性。
1 FPN及相關定義
本章介紹HFPN-RS涉及的相關概念[13,21-23]。
定義1 FPN。
定義2 前集、后集。
定義3 輸入庫所、輸出庫所、中間庫所、輸入庫所集、中間庫所集和輸出庫所集。
定義4 虛變遷、虛庫所。
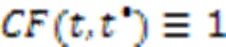
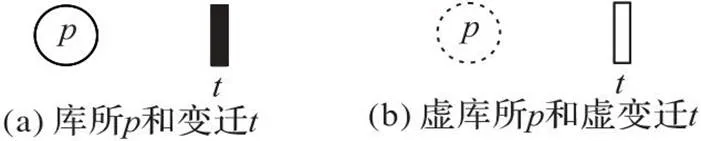
圖1 庫所和變遷、虛庫所和虛變遷
在分層過程中,虛庫所和虛變遷僅起中間過渡作用,除了增加模型的規模,對模型的知識表示和推理沒有造成其他影響。
定義5 直接可達集、可達集。
定義6 關聯矩陣。
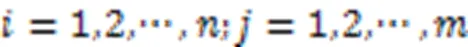
定義7 路徑、最長路徑。
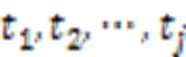
2 HFPN?RS
若FPN具有清晰的層次結構,需要滿足以下兩個條件:1)輸入庫所集的后集集合、輸出庫所集的前集集合分別劃分在同一層;2)除第一層和最后一層,其他每層變遷集合的后集等于下一層的前集,變遷集合的前集等于上一層的后集。因此,HFPN-RS的核心思想判斷當前庫所或變遷集合及其對應的后集集合是否在同一層,若不在同一層則通過添加虛庫所-虛變遷對調整層次結構。具體地,HFPN-RS通過添加虛庫所-虛變遷對實現層次劃分,可以分為以下3個步驟:
1)首先判斷當前變遷是否有額外的輸出,若存在,則在該變遷及其后集庫所間添加虛庫所-虛變遷對。
2)其次判斷當前庫所是否有額外的輸出,若存在,則在該庫所及其后集變遷間添加虛庫所-虛變遷對。
3)最后判斷當前層的前集是否等于輸入庫所集,若不相等,則需要在對應的輸入庫所及其后集變遷間添加虛庫所-虛變遷對。
2.1 HFPN-RS的步驟
結合上述算法設計思想,HFPN-RS的詳細步驟如算法1所示。
算法1 HFPN-RS。
輸入 庫所集、變遷集、輸入矩陣和輸出矩陣。
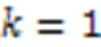
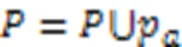
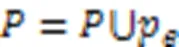
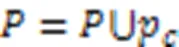
2.2 本文相關定理
在HFPN-RS的基礎上,給出兩個相關定理以確定FPN分層層數的下確界和最少需要添加的虛庫所-虛變遷對數。
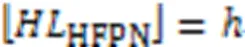


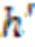
由上述分析可知,無論給定的FPN層次是否明確,經層次化操作后均可得到一個含有層的層次化明晰的FPN模型,即是一個確界。
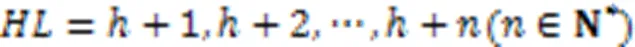
綜上所述,為保證任意給定FPN滿足層次化要求的最小分層層數,即FPN模型分層層數的下確界等于最長路徑長度。 證畢。
定義8 覆蓋路徑。

在求解最少添加的虛庫所-虛變遷對數時,通過計算當前路徑的覆蓋路徑在該路徑上添加的虛庫所-虛變遷對數避免重復計算需添加的虛庫所-虛變遷對,以保證整個FPN模型需添加的虛庫所-虛變遷對數最少。

2.3 HFPN-RS時間復雜度分析
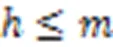
3 實驗與結果分析
通過Java語言編程實現HFPN-RS,并通過4個實驗案例驗證本文算法的有效性。由于虛庫所和虛變遷只起中間過渡作用,且相應的權值、閾值和確信度都已確定,因此本文實驗只驗證FPN模型的結構,未涉及其他FPN相關參數。實驗環境為Windows 11操作系統,JDK 1.8。編程語言為Java。
由第2章可知,若FPN模型具有清晰的層次結構,需要滿足以下兩個條件:
1)輸入庫所集的后集集合、輸出庫所集的前集集合分別劃分在同一層。
2)除第一層和最后一層外,其他每層變遷集合的后集等于下一層的前集,變遷集合的前集等于上一層的后集。
基于這兩點設計如下實驗:首先根據待分層的FPN模型得到它對應的輸入矩陣、輸出矩陣,并利用定理1、2預估新FPN模型的規模;其次將輸入矩陣、輸出矩陣作為HFPN-RS的輸入,運行分層算法(算法1)驗證定理,并輸出每一層的變遷集合、新FPN模型的關聯矩陣和矩陣的維度;最后根據關聯矩陣得到圖形化FPN,直觀展示新FPN清晰的層次結構。
從以下4種不同角度分別驗證HFPN-RS的正確性和魯棒性:
1)單輸入庫所FPN模型。
2)FPN模型庫所/變遷層次關系已經明確。
3)多輸入/輸出庫所,且輸入庫所、輸出庫所層次從屬關系不同。
4)中間庫所集、變遷的層次結構不明確,存在嵌套使用。
案例詳細實驗如下:
案例1 單輸入庫所FPN模型。待分層的FPN圖2所示。
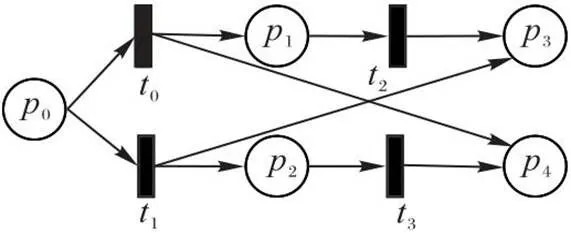
圖2 案例1的FPN模型



新生成的FPN如圖3所示。
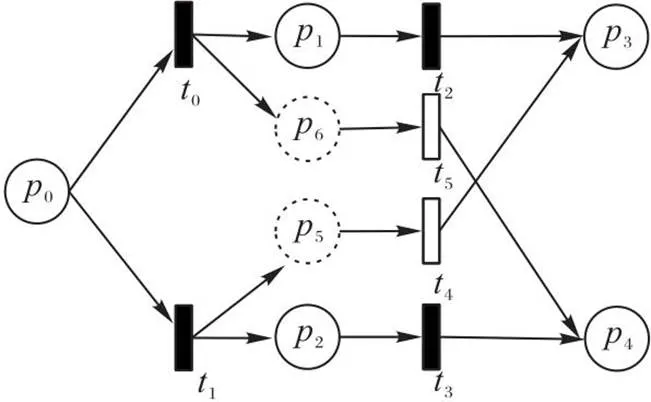
圖3 案例1層次化后的FPN模型
案例1得到的分層結果與文獻[20]中FPN的結構相同,都建立了清晰的層次結構,說明HFPN-RS同樣適用于模糊推理算法中連續函數的建立。
案例2 FPN模型庫所/變遷層次關系已經明確。待分層的FPN如圖4所示。
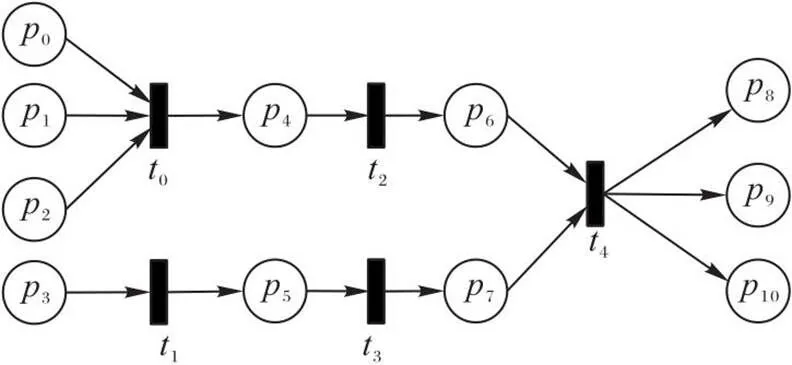
圖4 案例2的FPN模型

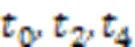

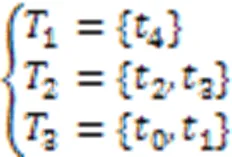
案例3 多輸入/輸出庫所,且輸入庫所、輸出庫所層次從屬關系不同。待分層的FPN如圖5所示。

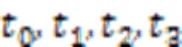
新的FPN如圖6所示。

圖6 案例3層次化后的FPN模型
案例4 中間庫所集、變遷的層次結構不明確,存在嵌套使用。待分層的FPN如圖7所示。

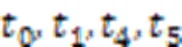

新的FPN如圖8所示。
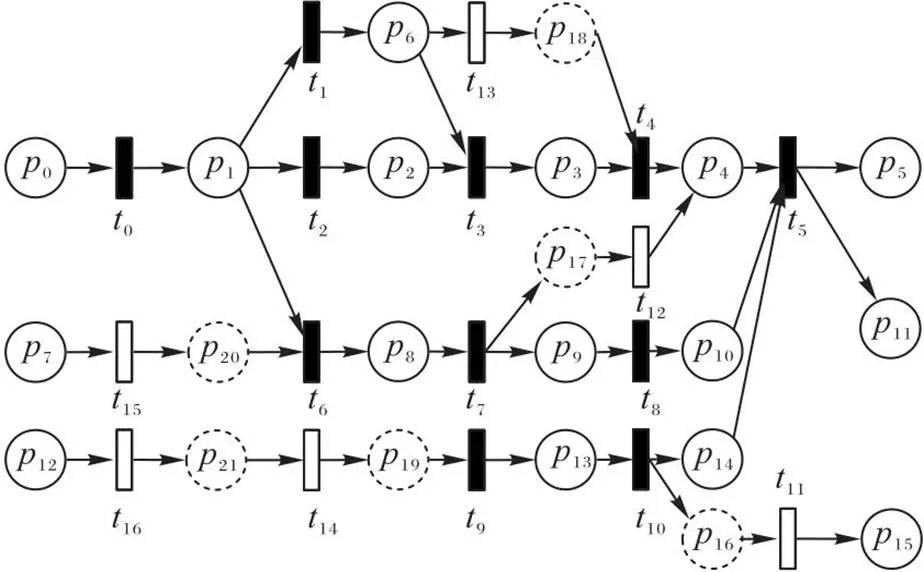
圖8 案例4層次化后的FPN模型
上述4種不同角度(單輸入庫所FPN模型;FPN模型庫所/變遷層次關系已經明確;多輸入/輸出庫所,且輸入庫所、輸出庫所層次從屬關系不同;中間庫所集、變遷的層次結構不明確,存在嵌套使用)的實驗案例都通過運行HFPN-RS得到了結構清晰、規模最小的HFPN,充分體現了HFPN-RS的正確性與魯棒性。同時,針對任意給定的FPN模型,由定理1、2預測得到HFPN的最小分層層數和添加虛庫所-虛變遷對的個數與實驗得到的完全一致,驗證了定理1、2的正確性。
4 結語
針對部分FPN不具有清晰的層次結構、庫所/變遷間從屬關系不明確的問題,本文提出了HFPN-RS以實現將非層次化FPN到HFPN的自動轉換。該算法從終結庫所出發,對整個FPN進行逆向搜索,將所有輸入庫所的后集、輸出庫所的前集分別劃分在同一層,再通過添加虛庫所-虛變遷對的方式最終使整個模型建立明確的層次結構。同時,相關定理的提出和證明從理論上明確了層次化FPN分層層數的下確界以及保證在得到的HFPN模型中添加的虛庫所-虛變遷數最少。在實驗部分,通過對幾類各具特點的FPN模型進行層次化操作,并利用所提定理進行驗證。下一步,將基于HFPN-RS深入研究提高FPN泛化能力的方法。
[1] ZHOU K-Q, ZAIN A M. Fuzzy Petri nets and industrial applications: a review[J]. Artificial Intelligence Review, 2015, 45(4):405-446.
[2] JIANG W, ZHOU K-Q, SARKHEYLI-H?GELE A, et al. Modeling, reasoning, and application of fuzzy Petri net model: a survey[J]. Artificial Intelligence Review, 2022, 55(8): 6567-6605.
[3] LIU H-C, YOU J-X, LI Z, et al. Fuzzy Petri nets for knowledge representation and reasoning: a literature review[J]. Engineering Applications of Artificial Intelligence, 2017, 60:45-56.
[4] LIU F, SUN W, HEINER M, et al. Hybrid modelling of biological systems using fuzzy continuous Petri nets[J]. Briefings in Bioinformatics, 2021, 22(1):438-450.
[5] HAMED R I. Quantitative modeling of gene networks of biological systems using fuzzy Petri nets and fuzzy sets[J]. Journal of King Saud University — Science, 2018, 30(1):112-119.
[6] YUAN C, LIAO Y, KONG L, et al. Fault diagnosis method of distribution network based on time sequence hierarchical fuzzy Petri nets [J]. Electric Power Systems Research, 2021, 191:106870.
[7] 劉敦楠,張潛,李霄彤,等. 基于云模型與模糊Petri網的電力市場潛在危害行為識別[J]. 電力系統自動化, 2019, 43(2):25-33.(LIU D N, ZHANG Q, LI X T, et al. Identification of potential harmful behaviors in electricity market based on cloud model and fuzzy Petri net[J]. Automation of Electric Power Systems, 2019, 43(2):25-33.)
[8] 胡濤,馬晨輝,周曉柳婷,等. 航天復雜系統的加權模糊Petri網故障診斷建模[J]. 計算機集成制造系統, 2019, 25(10):2580-2586.(HU T, MA C H, ZHOU X L T, et al. Fault diagnosis method for complex aerospace systems based on weighted fuzzy Petri net[J]. Computer Integrated Manufacturing Systems, 2019, 25(10):2580-2586.)
[9] WU Z, HSIEH S-J. A realtime fuzzy Petri net diagnoser for detecting progressive faults in PLC based discrete manufacturing system[J]. The International Journal of Advanced Manufacturing Technology, 2011, 61: 405-421.
[10] CHENG Y-H, YANG L-A. A fuzzy Petri nets approach for railway traffic control in case of abnormality: evidence from Taiwan railway system[J]. Expert Systems with Applications, 2009, 36(4):8040-8048.
[11] 戴晨曦,劉志剛,胡軻珽,等. 基于模型與模糊Petri網融合的高鐵牽引變壓器故障診斷[J]. 電力系統保護與控制, 2016, 44(11):26-32.(DAI C X, LIU Z G, HU K T, et al. Fault diagnosis for traction transformer of high speed railway on the integration of model-based diagnosis and fuzzy Petri nets[J]. Power System Protection and Control, 2016, 44(11): 26-32.)
[12] LI X, LARA-ROSANO F. Adaptive fuzzy Petri nets for dynamic knowledge representation and inference[J]. Expert Systems with Applications, 2000, 19(3):235-241.
[13] LI X, YU W, LARA-ROSANO F. Dynamic knowledge inference and learning under adaptive fuzzy Petri net framework[J]. IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), 2000, 30(4):442-450.
[14] WANG W-M, PENG X, ZHU G-N, et al. Dynamic representation of fuzzy knowledge based on fuzzy Petri net and genetic-particle swarm optimization[J]. Expert Systems with Applications, 2014, 41(4):1369-1376.
[15] TAN M, LI J, XU G, et al. A novel intuitionistic fuzzy inhibitor arc Petri net with error back propagation algorithm and application in fault diagnosis [J]. IEEE Access, 2019, 7:115978-115988.
[16] JIANG T, DU C, GUO S, et al. Microgrid fault diagnosis model based on weighted fuzzy neural Petri net [C]// Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference. Piscataway: IEEE, 2020: 2361-2365.
[17] WANG C, LI J, ZHU X, et al. Adaptive neural fuzzy Petri net algorithm for motor fault diagnosis[J]. IOP Conference Series: Earth and Environmental Science, 2020, 446:042063.
[18] LIN F-J, LIAO J-C, CHEN C-I, et al. Voltage restoration control for microgrid with recurrent wavelet Petri fuzzy neural network[J]. IEEE Access, 2022, 10:12510-12529.
[19] ZHOU K-Q, MO L-P, JIN J, et al. An equivalent generating algorithm to model fuzzy Petri net for knowledge-based system [J]. Journal of Intelligent Manufacturing, 2019, 30: 1831-1842.
[20] 鮑培明. 基于BP網絡的模糊Petri網的學習能力[J]. 計算機學報, 2004, 27(5):695-702.(BAO P M. Learning capability in fuzzy Petri nets based on BP net [J]. Chinese Journal of Computers, 2004, 27(5): 695-702.)
[21] ZHOU K-Q, ZAIN A M, MO L-P. Dynamic properties of fuzzy Petri net model and related analysis [J]. Journal of Central South University, 2015, 22:4717-4723.
[22] 孫曉玲. 直覺模糊Petri網的雙向模糊故障推理算法[J]. 計算機科學與探索, 2017, 11(6):1006-1013.(SUN X L. Bidirectional fuzzy fault reasoning algorithm of intuitionistic fuzzy Petri net[J]. Journal of Frontiers of Computer Science and Technology, 2017, 11(6): 1006-1013.)
[23] 莫禮平,樂曉波,周愷卿,等.帶抑制弧Petri網的保性變換[J].計算機應用, 2012,32(11):3071-3074.(MO L P, YUE X B, ZHOU K Q, et al. Property preserving operation for simplifying Petri nets with inhibitor arcs [J]. Journal of Computer Applications, 2012,32(11):3071-3074.)
Hierarchical algorithm of fuzzy Petri net by reverse search
XIANG Yinhong, ZHOU Kaiqing*, YANG Senyu, ZHANG Xuanyu, KANG Diwen
(,,416000,)
Fuzzy Petri Net (FPN) is one of the main tools to represent, model, and analyze the Knowledge-Based System (KBS). For clear hierarchical structures and uncertain affiliations between places/transactions in some FPNs, a Hierarchical algorithm of FPN by Reverse Search (HFPN-RS) was proposed to realize the automatic conversion from a non-hierarchical FPN to a Hierarchical FPN (HFPN). Firstly, a reverse search of the entire FPN was launched starting from the output place(s) at first. The front set of input place(s) and the back set of output place(s) were divided into the same layer. Then, the hierarchical structure of the entire FPN was clarified by adding virtual place-virtual transition pairs. Meanwhile, two theorems were proven to define the infimum of the number of hierarchical layers of FPN and the minimum number of virtual place-virtual transition pair(s) that need to be added in the hierarchical operation, respectively. Moreover, the dimension calculation formula of the incidence matrix of the complete hierarchical structure was also introduced. In the experimental part, hierarchical operation was performed on several types of FPN models with different characteristics and the proposed theorems were used to verify the HFPN-RS algorithm. The experimental results show that the new FPN has a clear hierarchical structure by adding the virtual place-virtual transition pair(s). It provides a theoretical base to further study the FPN generalization ability.
Fuzzy Petri Net (FPN); hierarchy; reverse search; virtual place-virtual transition pair; incidence matrix
This work is partially supported by National Natural Science Foundation of China (62066016), Scientific Research Project of Education Department of Hunan Province (22B0549,22C0282), Science Program Project of Xiangxi Prefecture (Prefecture Financial Education Index [2022] No.5), Postgraduate Scientific Research Innovation Project of Hunan Province (CX20231088).
XIANG Yinhong, born in 1998, M. S. candidate. His research interests include fuzzy Petri net, clinical assistant decision-making system.
ZHOU Kaiqing, born in 1984, Ph. D., associate professor. His research interests include fuzzy Petri net, clinical assistant diagnosis system, swarm intelligence algorithm.
YANG Senyu, born in 1999, M. S. candidate. His research interests include clinical assistant diagnosis system, swarm intelligence algorithm.
ZHANG Xuanyu, born in 1997, M. S. candidate. His research interests include fuzzy Petri net, clinical assistant diagnosis system.
KANG Diwen, born in 1997, M. S., assistant experimentist. His research interests include fuzzy Petri net, clinical assistant diagnosis system, swarm intelligence algorithm.
TP301
A
1001-9081(2023)12-3676-07
10.11772/j.issn.1001-9081.2022121851
2022?12?15;
2023?02?15;
2023?02?20。
國家自然科學基金資助項目(62066016);湖南省教育廳科學研究項目(22B0549, 22C0282);湘西州科學計劃項目(州財教指[2022]5號);湖南省研究生科研創新項目(CX20231088)。
向寅鴻(1998—),男,湖南常德人,碩士研究生,CCF會員,主要研究方向:模糊Petri網、臨床輔助決策系統;周愷卿(1984—),男,湖南長沙人,副教授,博士,CCF會員,主要研究方向:模糊Petri網、臨床輔助診斷系統、群智能算法;楊森宇(1999—),男,湖南吉首人,碩士研究生,主要研究方向:臨床輔助診斷系統、群智能算法;張軒宇(1997—),男,湖南長沙人,碩士研究生,CCF會員,主要研究方向:模糊Petri網、臨床輔助決策系統;康棣文(1997—),男,湖南長沙人,助理實驗師,碩士,CCF會員,主要研究方向:模糊Petri網、臨床輔助診斷系統、群智能算法。

