融合局部結(jié)構(gòu)學(xué)習(xí)的大規(guī)模子空間聚類(lèi)算法

任奇澤，賈洪杰，陳東宇

融合局部結(jié)構(gòu)學(xué)習(xí)的大規(guī)模子空間聚類(lèi)算法

任奇澤，賈洪杰*，陳東宇

（江蘇大學(xué) 計(jì)算機(jī)科學(xué)與通信工程學(xué)院，江蘇 鎮(zhèn)江 212013）（?通信作者電子郵箱jiahj@ujs.edu.cn）

常規(guī)的大規(guī)模子空間聚類(lèi)算法在計(jì)算錨點(diǎn)親和矩陣時(shí)忽略了數(shù)據(jù)之間普遍存在的局部結(jié)構(gòu)，且在計(jì)算拉普拉斯（Laplacian）矩陣的近似特征向量時(shí)存在較大誤差，不利于數(shù)據(jù)聚類(lèi)。針對(duì)上述問(wèn)題，提出一種融合局部結(jié)構(gòu)學(xué)習(xí)的大規(guī)模子空間聚類(lèi)算法（LLSC）。所提算法將局部結(jié)構(gòu)學(xué)習(xí)嵌入錨點(diǎn)親和矩陣的學(xué)習(xí)，從而能夠綜合利用全局和局部信息挖掘數(shù)據(jù)的子空間結(jié)構(gòu)；此外，受非負(fù)矩陣分解（NMF）的啟發(fā)，設(shè)計(jì)一種迭代優(yōu)化方法以簡(jiǎn)化錨點(diǎn)親和矩陣的求解過(guò)程；其次，根據(jù)Nystr?m近似方法建立錨點(diǎn)親和矩陣與Laplacian矩陣的數(shù)學(xué)聯(lián)系，并改進(jìn)Laplacian矩陣特征向量的計(jì)算方法以提升聚類(lèi)性能。相較于LMVSC（Large-scale Multi-View Subspace Clustering）、SLSR（Scalable Least Square Regression）、LSC-k（Landmark-based Spectral Clustering using k-means）和k-FSC（k-Factorization Subspace Clustering），LLSC在4個(gè)廣泛使用的大規(guī)模數(shù)據(jù)集上顯示出明顯的提升，其中，在Pokerhand數(shù)據(jù)集上，LLSC的準(zhǔn)確率比k-FSC高28.18個(gè)百分點(diǎn)，驗(yàn)證了LLSC的有效性。

子空間聚類(lèi)；局部結(jié)構(gòu)學(xué)習(xí)；非負(fù)矩陣分解；大規(guī)模聚類(lèi)；低秩近似

0 引言

聚類(lèi)作為一種無(wú)監(jiān)督數(shù)據(jù)分析工具，一直是機(jī)器學(xué)習(xí)和數(shù)據(jù)挖掘領(lǐng)域中非常重要的研究課題。隨著信息技術(shù)的不斷發(fā)展，高維數(shù)據(jù)無(wú)處不在。高維數(shù)據(jù)具有低維的子空間結(jié)構(gòu)，因此傳統(tǒng)聚類(lèi)算法在處理高維數(shù)據(jù)時(shí)性能較差，使用相似性度量方法的效率低下，可視化和理解輸入變得困難。為解決上述問(wèn)題，通常使用降維技術(shù)，但該技術(shù)會(huì)引發(fā)“維度詛咒”，即隨著維度增加，所有子空間的完整枚舉變得難以處理；其次，數(shù)據(jù)的多個(gè)維度之間可能不相關(guān)，在有噪聲的數(shù)據(jù)中可能屏蔽現(xiàn)有的聚類(lèi)。因此，子空間聚類(lèi)作為一個(gè)基本的問(wèn)題，已經(jīng)成為了熱門(mén)話題。近些年，很多經(jīng)典的子空間聚類(lèi)算法被提出，在這些算法中基于稀疏自表示模型的算法［1］、基于低秩近似的算法［2］都取得了成就。稀疏自表示模型發(fā)現(xiàn)了數(shù)據(jù)的稀疏表示，低秩近似發(fā)現(xiàn)了子空間低秩的結(jié)構(gòu)。這些子空間算法在各大領(lǐng)域中被廣泛應(yīng)用，如信息安全［3］、圖像聚類(lèi)［4］、大數(shù)據(jù)分析和圖像檢測(cè)［5］等。研究人員在這些領(lǐng)域利用子空間聚類(lèi)實(shí)現(xiàn)檢測(cè)數(shù)據(jù)、識(shí)別圖片和過(guò)濾噪聲樣本等功能。

現(xiàn)有的子空間聚類(lèi)算法需要精確估計(jì)底層子空間的維度，會(huì)提高子空間聚類(lèi)計(jì)算復(fù)雜度，多種情況下無(wú)法使用；此外，相關(guān)的優(yōu)化問(wèn)題都是非凸的，良好的初始化對(duì)找到最優(yōu)解非常重要［6］。現(xiàn)有的子空間聚類(lèi)通常使用譜聚類(lèi)算法解決問(wèn)題：通過(guò)觀測(cè)樣本得到一個(gè)相似矩陣，然后對(duì)這個(gè)矩陣進(jìn)行譜聚類(lèi)獲得最終的聚類(lèi)結(jié)果。譜聚類(lèi)是一種基于圖劃分的聚類(lèi)算法，能夠處理具有復(fù)雜非線性結(jié)構(gòu)的真實(shí)數(shù)據(jù)，在非凸模式和線性不可分簇中表現(xiàn)良好；但是譜聚類(lèi)需要計(jì)算拉普拉斯（Laplacian）矩陣的特征向量，內(nèi)存需求非常大，計(jì)算復(fù)雜度也很高，面對(duì)大規(guī)模數(shù)據(jù)時(shí)適用性受限。He等［7］設(shè)計(jì)一種大規(guī)模的譜聚類(lèi)，通過(guò)使用隨機(jī)傅里葉特征顯式地表示核空間中的數(shù)據(jù)。Kang等［8］提出一種具有線性復(fù)雜度的大規(guī)模子空間聚類(lèi)（Large-Scale Subspace Clustering，LS2C）算法處理大規(guī)模數(shù)據(jù)。這些算法通過(guò)計(jì)算并使用較小的錨點(diǎn)親和矩陣的特征向量逼近Laplacian矩陣的特征向量，不僅規(guī)避了大規(guī)模構(gòu)圖的問(wèn)題，而且在避免計(jì)算復(fù)雜度過(guò)高的同時(shí)降低了聚類(lèi)復(fù)雜度。

雖然現(xiàn)有的LS2C已經(jīng)取得較大成果，但它通常忽略局部相似性的重要性。在變換后的低維空間中，保持高維數(shù)據(jù)的內(nèi)在信息非常重要，使用單一的特征無(wú)法完全表示數(shù)據(jù)底層結(jié)構(gòu)，而全局和局部的特征都是重要的。局部的特征對(duì)近鄰大小敏感，不同子空間交點(diǎn)周邊的點(diǎn)也具有較強(qiáng)的捕獲能力，因?yàn)樗蕾嚦蓪?duì)距離的相似矩陣；而且數(shù)據(jù)的局部幾何結(jié)構(gòu)可被視作數(shù)據(jù)相關(guān)的正則化，有助于避免過(guò)擬合［9］。

此外，已有的LS2C算法將錨點(diǎn)親和矩陣優(yōu)化問(wèn)題視作凸二次規(guī)劃問(wèn)題，但很多凸二次規(guī)劃求解方法不能始終滿足錨點(diǎn)親和矩陣的非負(fù)限制。非負(fù)矩陣分解（Nonnegative Matrix Factorization， NMF）中使用的迭代優(yōu)化方法可以幫助解決錨點(diǎn)親和矩陣的優(yōu)化問(wèn)題［10］。NMF將原始的非負(fù)數(shù)據(jù)矩陣分解為非負(fù)基矩陣和非負(fù)系數(shù)矩陣，使它們的乘積能夠最接近原始非負(fù)數(shù)據(jù)矩陣。而非負(fù)拉格朗日松弛［11］作為一種受NMF啟發(fā)產(chǎn)生的非負(fù)松弛方法，通過(guò)將非負(fù)約束吸收到目標(biāo)函數(shù)，保證錨點(diǎn)親和矩陣的計(jì)算過(guò)程是非負(fù)的。

LS2C獲得錨點(diǎn)親和矩陣后，通常需要計(jì)算Laplacian矩陣的特征向量，用于聚類(lèi)分析。已有的LS2C使用學(xué)習(xí)的錨點(diǎn)親和矩陣構(gòu)造了一個(gè)矩陣逼近Laplacian矩陣；但該方法無(wú)法保證最佳的低秩近似，也難以有效地捕獲子空間結(jié)構(gòu)。Fowlkes等［12］采用Nystr?m近似方法［13］，用較小的樣本子矩陣的特征向量逼近較大的原Laplacian矩陣的特征向量。Nystr?m近似方法可以保證最佳的低秩近似，且計(jì)算復(fù)雜度較低。

綜上，已有的LS2C算法的缺點(diǎn)包括：1）只考慮全局性的結(jié)構(gòu)，忽略數(shù)據(jù)之間的普遍存在的局部結(jié)構(gòu)；2）錨點(diǎn)矩陣的優(yōu)化過(guò)于昂貴；3）使用親和矩陣構(gòu)造的一個(gè)矩陣逼近Laplacian矩陣，無(wú)法保證最佳的低秩近似，難以有效地捕獲子空間結(jié)構(gòu)。針對(duì)以上缺點(diǎn)，本文提出一種融合局部結(jié)構(gòu)學(xué)習(xí)的LS2C算法（LS2C algorithm with Local structure learning， LLSC）。

本文的主要工作如下：

1）在LS2C的目標(biāo)函數(shù)中加入局部結(jié)構(gòu)項(xiàng)，使學(xué)習(xí)的錨點(diǎn)親和矩陣能同時(shí)保留數(shù)據(jù)的局部特征和全局特征。

2）利用非負(fù)拉格朗日松弛［11］的特性，設(shè)計(jì)了一種類(lèi)似于NMF的迭代更新規(guī)則優(yōu)化目標(biāo)函數(shù)。利用非負(fù)拉格朗日松弛計(jì)算錨點(diǎn)親和矩陣，可以更有效地捕獲子空間結(jié)構(gòu)，從而反映數(shù)據(jù)之間的真實(shí)聯(lián)系。

3）引入Nystr?m近似方法求解Laplacian矩陣的特征向量，保證最佳的低秩近似，改善聚類(lèi)結(jié)果。

4）通過(guò)在有挑戰(zhàn)的數(shù)據(jù)集上進(jìn)行實(shí)驗(yàn)，驗(yàn)證了所提算法的有效性。

1 相關(guān)工作

1.1　LS2C

子空間聚類(lèi)因良好的性能而得到了廣泛的研究［14］，被眾多的領(lǐng)域關(guān)注。子空間聚類(lèi)的重點(diǎn)是計(jì)算表示系數(shù)矩陣。從高維數(shù)據(jù)中搜尋一個(gè)最具有代表性的低維子空間一直都是機(jī)器學(xué)習(xí)和計(jì)算機(jī)視覺(jué)領(lǐng)域的一個(gè)重要課題。子空間聚類(lèi)作為一種在不同子空間發(fā)現(xiàn)聚類(lèi)的技術(shù)，在信息采集和數(shù)據(jù)處理技術(shù)中得到廣泛應(yīng)用。隨著大數(shù)據(jù)時(shí)代的發(fā)展，研究人員從不同的角度提高聚類(lèi)精度和降低處理相似性矩陣的時(shí)間復(fù)雜度，許多LS2C算法被相繼提出。Li等［15］開(kāi)發(fā)了一個(gè)可學(xué)習(xí)的子空間聚類(lèi)，有效地解決LS2C問(wèn)題，該算法選擇學(xué)習(xí)一個(gè)參數(shù)函數(shù)將高維子空間劃分為它底層的低維子空間。Huang等［16］提出一種基于大規(guī)模稀疏子空間聚類(lèi)（Sparse Subspace Clustering， SSC）的聚類(lèi)算法，在不犧牲聚類(lèi)精度的前提下高效地處理大規(guī)模高光譜圖像集。Zhou等［17］提出一種基于克羅內(nèi)克（Kronecker）積的子空間聚類(lèi)算法，根據(jù)塊對(duì)角矩陣與其他矩陣的Kronecker乘積仍然是塊對(duì)角矩陣的性質(zhì)，有效地學(xué)習(xí)由個(gè)更小矩陣的Kronecker乘積構(gòu)成的表示矩陣（為簇類(lèi)個(gè)數(shù)）。Li等［18］通過(guò)考慮一個(gè)LS2C問(wèn)題，即用百萬(wàn)維度劃分百萬(wàn)數(shù)據(jù)點(diǎn)，通過(guò)劃分大數(shù)據(jù)變量矩陣和正規(guī)化的列和行，設(shè)計(jì)一個(gè)獨(dú)立的分布式并行的框架。Fan等［19］提出一種LS2C的k因子分解子空間聚類(lèi)算法k-FSC（k-Factorization Subspace Clustering）。k-FSC通過(guò)在矩陣分解模型中追求結(jié)構(gòu)化稀疏性，將數(shù)據(jù)直接分解為個(gè)，并學(xué)習(xí)親和矩陣和特征值分解，在大數(shù)據(jù)集上具有較低的（線性）時(shí)間和空間復(fù)雜度。Feng等［20］提出一種使用SSC挖掘鑒別特征的算法，解決大規(guī)模圖像集分類(lèi)問(wèn)題，并使用兩兩線性回歸分類(lèi)完成最終的分類(lèi)任務(wù)。Si等［21］提出一種新的具有結(jié)構(gòu)約束的一致且多樣性多視圖子空間聚類(lèi)算法（Consistent and Diverse Multi-view Subspace Clustering algorithm with structure constraint， CDMSC）。CDMSC首先使用排他性約束項(xiàng)增強(qiáng)不同視圖之間特定表示的多樣性，其次通過(guò)將學(xué)習(xí)的子空間自表示分解為聚類(lèi)質(zhì)心和聚類(lèi)分配，將聚類(lèi)結(jié)構(gòu)約束施加到子空間自表達(dá)，獲得面向聚類(lèi)的子空間自我表示。對(duì)于無(wú)法準(zhǔn)確描述樣本之間的線性關(guān)系與難找到理想的相似性矩陣的問(wèn)題，Xu等［22］提出一種線性感知子空間聚類(lèi)算法（Linearity-Aware Subspace Clustering algorithm， LASC），通過(guò)使用線性感知度量學(xué)習(xí)相似性矩陣。LASC將度量學(xué)習(xí)和子空間聚類(lèi)結(jié)合到一個(gè)聯(lián)合學(xué)習(xí)框架，并用自表達(dá)策略獲得初始子空間結(jié)構(gòu)以探索原始數(shù)據(jù)的低維表示。

1.2　大規(guī)模譜聚類(lèi)

譜聚類(lèi)是最流行的聚類(lèi)算法之一，具有良好的性能，但計(jì)算復(fù)雜度高，對(duì)大規(guī)模問(wèn)題的適用性一直受限。為了將譜聚類(lèi)算法擴(kuò)展到大規(guī)模的數(shù)據(jù)，近年來(lái)，研究者們提出了許多加速譜聚類(lèi)的算法。Wang等［23］提出結(jié)構(gòu)化低秩表示描述不同數(shù)據(jù)視圖的聚類(lèi)結(jié)構(gòu)，并使用多視圖共識(shí)結(jié)構(gòu)提高聚類(lèi)性能。崔藝馨等［24］提出一種大規(guī)模譜聚類(lèi)的并行化算法處理大規(guī)模數(shù)據(jù)。Zhu等［25］提出了一種低秩SSC算法，將原始數(shù)據(jù)投影到低維空間，并從新空間動(dòng)態(tài)學(xué)習(xí)相似矩陣。Hu等［26］設(shè)計(jì)一種結(jié)合非負(fù)嵌入和譜嵌入的無(wú)參數(shù)聚類(lèi)算法，降低多視圖譜聚類(lèi)的高計(jì)算成本。為了加速大規(guī)模問(wèn)題的譜聚類(lèi)，Wang等［27］提出了一種基于隨機(jī)游走Laplacian方法的快速譜聚類(lèi)算法，利用隨機(jī)游走Laplacian算子明確地平衡錨的普及性和數(shù)據(jù)點(diǎn)的獨(dú)立性。Yang等［28］提出了一種大規(guī)模譜聚類(lèi)算法，該算法將超圖擴(kuò)展成一種通用格式，以捕獲復(fù)雜的高階關(guān)系，并解決大規(guī)模超圖譜聚類(lèi)中的可擴(kuò)展性問(wèn)題。Zhao等［29］提出了一種可擴(kuò)展的多級(jí)算法用于大型無(wú)向圖的譜嵌入，該算法使用一種接近線性時(shí)間的譜圖粗化方法計(jì)算一個(gè)更小的稀疏圖，同時(shí)保留原始圖的關(guān)鍵譜（結(jié)構(gòu)）特性。El Hajjar等［30］提出了一種基于一步圖的多視圖聚類(lèi)算法，使用與數(shù)據(jù)空間關(guān)聯(lián)的圖的聚類(lèi)標(biāo)簽相關(guān)性構(gòu)建額外的圖，并對(duì)聚類(lèi)標(biāo)簽矩陣施加平滑約束，使它與原始數(shù)據(jù)圖和標(biāo)簽圖更一致。Inoubli等［31］提出了一種基于結(jié)構(gòu)圖聚類(lèi)的分布式圖聚類(lèi)算法。針對(duì)大規(guī)模多視圖總是遇到高復(fù)雜性和昂貴的時(shí)間開(kāi)銷(xiāo)的問(wèn)題，Wang等［32］提出一種基于二部圖框架的靈活高效的不完全大規(guī)模多視圖聚類(lèi)算法，通過(guò)將多視圖錨學(xué)習(xí)和不完全二分圖形式轉(zhuǎn)化為一個(gè)相互協(xié)調(diào)統(tǒng)一的框架以提高聚類(lèi)算法的性能。He等［33］提出了一種新的結(jié)構(gòu)化錨推斷圖學(xué)習(xí)算法（Structured Anchor-inferred Graph Learning algorithm， SAGL）。SAGL不僅可以解決具有挑戰(zhàn)性的不完全多視圖譜聚類(lèi)問(wèn)題，還能處理任意視圖缺失情況；此外，SAGL能夠捕獲多視圖數(shù)據(jù)之間的隱藏連接信息，從而提高聚類(lèi)性能。

1.3　NMF

NMF作為流行且重要的矩陣分解之一，是一種分析非負(fù)數(shù)據(jù)的線性降維技術(shù)。NMF起源于Paatero等［34］提出的正矩陣分解，此后Lee等［35］為NMF開(kāi)發(fā)了一種簡(jiǎn)單有效的乘法更新算法。Lu等［36］提出了一種子空間聚類(lèi)約束稀疏的NMF算法（Subspace Clustering constrained sparse NMF， SC-NMF）用于高光譜分解，以更準(zhǔn)確地提取端元和相應(yīng)的豐度。但是一些NMF算法嚴(yán)重受到噪聲數(shù)據(jù)的影響，既無(wú)法保留數(shù)據(jù)的幾何信息，也無(wú)法保證稀疏部分的表示。針對(duì)上述問(wèn)題，Peng等［37］提出了一種基于相關(guān)熵的雙圖正則化局部坐標(biāo)約束NMF算法（correntropy based Dual graph regularized NMF algorithm with Local Coordinate constraint， LCDNMF），將數(shù)據(jù)流形和特征流形的幾何信息和局部坐標(biāo)約束合并到基于相關(guān)熵的目標(biāo)函數(shù)。Zhang等［38］提出了一種具有自適應(yīng)權(quán)重的多圖正則化半監(jiān)督NMF算法，以捕獲判別數(shù)據(jù)表示。Peng等［39］提出了一種新的NMF算法，以相互增強(qiáng)的方式學(xué)習(xí)局部相似性和聚類(lèi)。Gillis等［40］設(shè)計(jì)了一個(gè)基于乘法更新的簡(jiǎn)單算法，解決多目標(biāo)NMF問(wèn)題。Leplat等［41］針對(duì)任意散度的多分辨率NMF問(wèn)題提出了一種基于乘法更新的新算法。Liu等［42］提出了一種魯棒多視圖NMF聚類(lèi)算法，可以解決大多數(shù)多視圖聚類(lèi)難以充分探索鄰域信息等問(wèn)題。Fan等［43］提出一種水印算法，將經(jīng)過(guò)加密的二維碼版權(quán)水印嵌入NMF基矩陣，以提高水印在不可見(jiàn)條件下的抗攻擊能力。

2 本文算法

表1是本文所用符號(hào)的描述。

表1　符號(hào)及其描述

2.1　問(wèn)題定義

本文將式（1）中的正則化函數(shù)修改為局部學(xué)習(xí)項(xiàng)，引入局部學(xué)習(xí)可以更有效地捕獲子空間結(jié)構(gòu)，借用錨的思想，將視為字典。最后利用式（3）學(xué)習(xí)錨點(diǎn)親和矩陣：

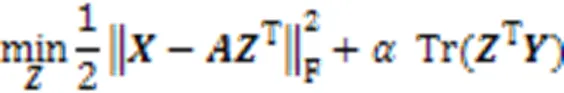
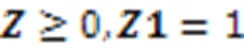
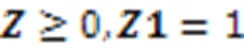
2.2　迭代求解矩陣Z

通過(guò)非負(fù)拉格朗日松弛的方法優(yōu)化目標(biāo)函數(shù)。使用式（5）更新式（4）并求解式（4），元素更新如下：

更新的正確性和收斂性證明如下。對(duì)于式（5）的更新規(guī)則，本文給出了以下兩個(gè)主要結(jié)論：1）收斂時(shí)，式（5）極限解滿足KKT（Karush-Kuhn-Tucker）條件，KKT條件是非線性規(guī)劃最優(yōu)解的必要條件；2）式（5）迭代收斂。本文將在定理1中正式建立上述結(jié)果。

定理1 在更新矩陣時(shí)，式（5）中更新規(guī)則的極限解滿足KKT條件。

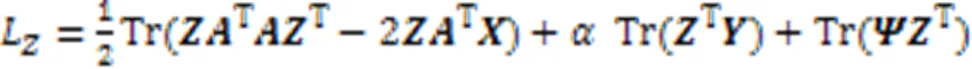
由式（6）的轉(zhuǎn)換，得到式（7）：

式（10）提供了極限解應(yīng)滿足的不動(dòng)點(diǎn)條件。可以看到，式（5）的極限解滿足式（9），描述如下：

式（10）被簡(jiǎn)化為式（11）：

2.3　Nystr?m近似

為了構(gòu)造Laplacian矩陣，需要計(jì)算度矩陣，為×的對(duì)角矩陣，由式（15）計(jì)算：

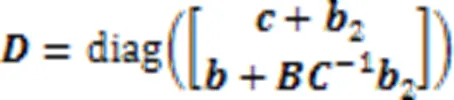
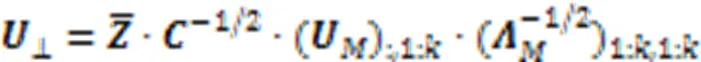
算法1是的本文算法LLSC的總體流程。

算法1 LLSC。

輸出 聚類(lèi)結(jié)果。

3 實(shí)驗(yàn)與結(jié)果分析

3.1　評(píng)估指標(biāo)

實(shí)驗(yàn)使用4個(gè)聚類(lèi)指標(biāo)評(píng)估聚類(lèi)性能，包括聚類(lèi)準(zhǔn)確率（Accuracy，Acc）、歸一化互信息（Normalized Mutual Information， NMI）、純度（Purity）和運(yùn)行時(shí)間（Time）［46］。Acc衡量每個(gè)類(lèi)簇包含來(lái)自同一類(lèi)的數(shù)據(jù)點(diǎn)的準(zhǔn)確率；NMI使用信息熵衡量類(lèi)簇標(biāo)簽與真實(shí)標(biāo)簽的相符程度；Purity衡量每個(gè)簇中的數(shù)據(jù)點(diǎn)來(lái)自同一類(lèi)樣本的程度。以上指標(biāo)的值越高，表明聚類(lèi)質(zhì)量越好。運(yùn)行時(shí)間（Time）衡量聚類(lèi)的速率，運(yùn)行時(shí)間越少，表明聚類(lèi)效率越高。

給定一個(gè)聚類(lèi)結(jié)果標(biāo)簽和對(duì)應(yīng)的真實(shí)標(biāo)簽，Acc的計(jì)算公式如下：

NMI的計(jì)算方式如下：

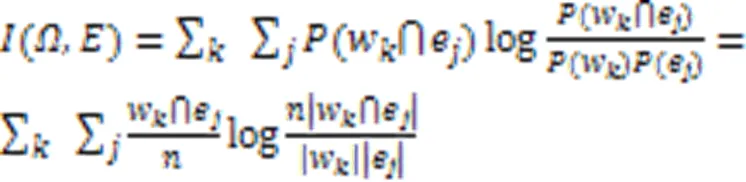
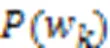
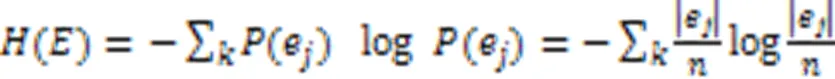
Purity的計(jì)算方式如下所示：

實(shí)驗(yàn)過(guò)程中，需要根據(jù)不同的數(shù)據(jù)集調(diào)整聚類(lèi)算法的參數(shù)，以獲得最佳性能。很多LS2C算法的聚類(lèi)性能取決于采樣的結(jié)果。因此，每次參數(shù)運(yùn)行20次，每次使用不同的采樣率，并記錄最佳聚類(lèi)結(jié)果。所有實(shí)驗(yàn)都在一臺(tái)4.6 GHz Intel CPU和64 GB RAM、Matlab R2019b的惠普工作站上實(shí)現(xiàn)。為了公平比較，實(shí)驗(yàn)過(guò)程中嚴(yán)格遵循相關(guān)論文中描述的實(shí)驗(yàn)設(shè)置，調(diào)整參數(shù)以獲得最佳性能。

3.2　小規(guī)模數(shù)據(jù)集上的實(shí)驗(yàn)和結(jié)果分析

首先在幾個(gè)小型數(shù)據(jù)集上進(jìn)行測(cè)試：RCV1_4和Tr45是文本語(yǔ)料庫(kù)，USPS是手寫(xiě)數(shù)據(jù)。表2總結(jié)了這些數(shù)據(jù)集的具體信息。

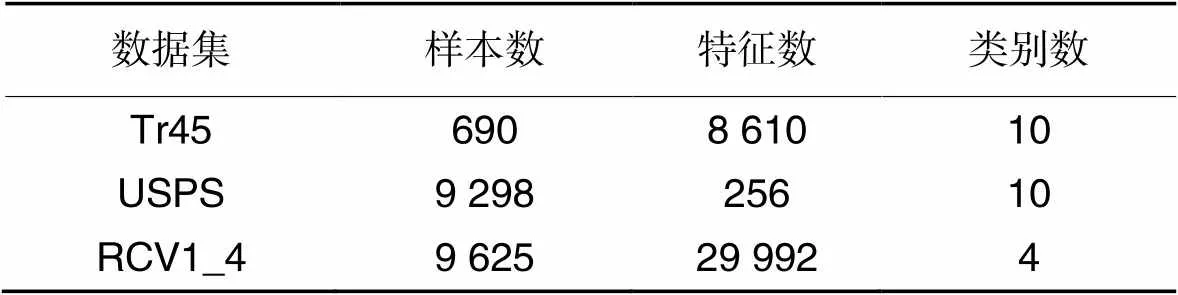
表2　小規(guī)模數(shù)據(jù)集的具體信息

將LLSC與以下聚類(lèi)算法進(jìn)行比較：

1）LMVSC（Large-scale Multi-View Subspace Clustering）［8］。最先進(jìn)的大規(guī)模聚類(lèi)算法之一。

2）SGL （Structured Graph Learning）［47］。一種結(jié)構(gòu)化圖學(xué)習(xí)可伸縮的子空間聚類(lèi)算法。

3）FNC （Fast Normalized Cut）［48］。一種直接求解歸一化切割算法，具有較低的計(jì)算復(fù)雜度。

4）KMM （K-Multiple-Means）［49］。基于二分圖劃分的K-多重均值算法。

LLSC中一共有和兩個(gè)參數(shù)。首先，在小規(guī)模數(shù)據(jù)的采樣上，對(duì)比算法統(tǒng)一在［100，1 000］搜索最優(yōu)平均解進(jìn)行對(duì)比；但由于Tr45過(guò)小，采樣區(qū)間設(shè)置在［100，300］。的參數(shù)在［0.001，100］選擇。

不同的數(shù)據(jù)集的樣本分布有很大差異，不同算法在不同的數(shù)據(jù)集上運(yùn)行時(shí)間和聚類(lèi)結(jié)果也有差異。針對(duì)小規(guī)模數(shù)據(jù)集進(jìn)行實(shí)驗(yàn)和結(jié)果分析。表3展示了LLSC和對(duì)比算法在不同小規(guī)模數(shù)據(jù)集上的聚類(lèi)結(jié)果。

表3　小規(guī)模數(shù)據(jù)集上的聚類(lèi)結(jié)果

注：粗體表示最佳性能值。

在Acc和Time上，LLSC明顯優(yōu)于對(duì)比算法。在Tr45數(shù)據(jù)集上，LLSC的NMI和Purity比LMVSC高4.91和11.74個(gè)百分點(diǎn)。在Tr45數(shù)據(jù)集上，LLSC的Acc結(jié)果是77.24%，SGL和KMM的Acc分別是74.41%和73.8%，數(shù)值上LLSC的提升較低，這是因?yàn)長(zhǎng)LSC主要針對(duì)大規(guī)模數(shù)據(jù)集，在具有挑戰(zhàn)的小規(guī)模的數(shù)據(jù)集上的聚類(lèi)優(yōu)勢(shì)不明顯。在Acc、Purity和NMI方面，LLSC在USPS數(shù)據(jù)集上都高于對(duì)比算法。例如：LLSC在USPS上Acc、NMI和Purity比LMVSC高12.25、14.97和8.04個(gè)百分點(diǎn)。此外，LLSC在USPS上的Time也是所有算法中最少的，僅使用了1.00 s。在RCV1_4數(shù)據(jù)集上，LLSC用時(shí)0.17 s，遠(yuǎn)低于LMVSC的585.00 s。KMM雖然效率高，但是聚類(lèi)結(jié)果較差。在RCV1_4上，SGL的NMI和Purity最優(yōu)，但是它的Time較差，LLSC僅用0.17 s，而SGL則需要98.86 s。因此，在小規(guī)模的數(shù)據(jù)集上LLSC優(yōu)于對(duì)比算法。

3.3　大規(guī)模數(shù)據(jù)集上的實(shí)驗(yàn)和結(jié)果分析

表4總結(jié)了大規(guī)模數(shù)據(jù)集的具體信息。MNIST和EMNIST（digits）是圖像數(shù)據(jù)，Postures是手寫(xiě)數(shù)據(jù)，Pokerhand是牌手?jǐn)?shù)據(jù)。

LLSC將與以下大規(guī)模的聚類(lèi)算法進(jìn)行比較：

1）LMVSC［8］。最先進(jìn)的大規(guī)模聚類(lèi)算法之一。

2）LSC-k（Landmark-based Spectral Clustering using k-means）［50］。最傳統(tǒng)的大規(guī)模譜聚類(lèi)算法之一。

3）SLSR（Scalable Least Square Regression）［51］。最傳統(tǒng)的大規(guī)模數(shù)據(jù)子空間聚類(lèi)之一。

4）k-FSC［19］。一種最新的LS2C。

在這些數(shù)據(jù)集中，LLSC和對(duì)比算法的采樣數(shù)都在［500，3 000］搜索最優(yōu)解。參數(shù)在［0.001，100］選擇最優(yōu)值。

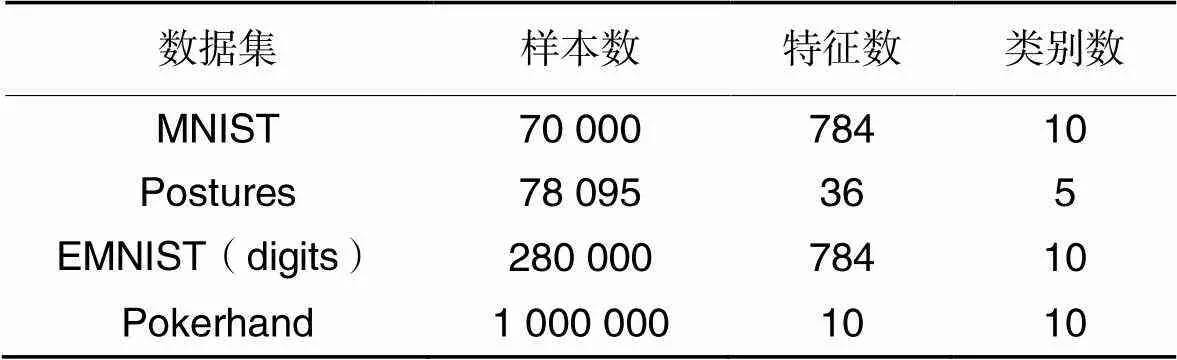
表4　大規(guī)模數(shù)據(jù)集的具體信息

表5顯示了各種算法在MNIST和Postures數(shù)據(jù)集上的聚類(lèi)結(jié)果，由表5可以看出，在Acc和Time上，LLSC在大多數(shù)情況下明顯優(yōu)于其他對(duì)比算法。在MNIST上，LLSC用時(shí)最少，表明LLSC聚類(lèi)效率高于其他對(duì)比算法，例如：LMVSC用了73.33 s，而LLSC只用了3.71 s。在MNIST上，LLSC的Acc比LMVSC僅提高了2.39個(gè)百分點(diǎn)。雖然LSC-k的Acc高于LLSC，但是LLSC的Time遠(yuǎn)低于LSC-k。在Postures上，LLSC表現(xiàn)出來(lái)的效果要比所對(duì)比的算法好許多，在Acc和NMI這兩個(gè)指標(biāo)上，LLSC比LMVSC和SLSR高28.10、31.11個(gè)百分點(diǎn)和11.01、3.06個(gè)百分點(diǎn)。且LLSC的聚類(lèi)效率也得到了很大的提升。k-FSC在Postures上的聚類(lèi)效果次優(yōu)。LLSC的Time也是所對(duì)比中最少的。雖然SLSR的Time次優(yōu)，但是聚類(lèi)效果比LLSC和k-FSC差。

表5　MNIST和Postures數(shù)據(jù)集上的聚類(lèi)結(jié)果

表6展示了LLSC和對(duì)比算法在Pokerhand和EMNIST（digits）數(shù)據(jù)集上的聚類(lèi)結(jié)果。此外，LLSC的Acc比LMVSC、LSC-k分別高出36.32、37.68個(gè)百分點(diǎn)。在Pokerhand數(shù)據(jù)集上，雖然LLSC和k-FSC的Time相差較小，但LLSC的Acc比k-FSC高28.18個(gè)百分點(diǎn)，在Pokerhand上面LLSC具有一個(gè)比較好的提升。盡管SLSR在Pokerhand數(shù)據(jù)集上的Time最優(yōu)，但是它的Acc并不理想。在EMNIST（digits）上，LMVSC由于采樣數(shù)為300時(shí)聚類(lèi)需要消耗7 867 s，因此放棄對(duì)LMVSC采樣1 000，LLSC比LMVSC和SLSR在Acc和NMI上分別高15.26、17.4個(gè)百分點(diǎn)和8.7、22.68個(gè)百分點(diǎn)。此外，LLSC的Time非常低，如：LLSC用時(shí)12.54 s，SLSR用時(shí)182.52 s。對(duì)比算法都基于錨圖，這些算法在近似求解Laplacian矩陣的特征向量時(shí)使用奇異值分解（Singular Value Decomposition， SVD）方法，這種方法計(jì)算復(fù)雜度過(guò)高，聚類(lèi)的Time將提高，而LLSC使用的Nystr?m可以解決這個(gè)問(wèn)題。雖然SLSR在Pokerhand上的效率高于LLSC，但是SLSR的聚類(lèi)精度要遠(yuǎn)低于LLSC。可以得出LLSC在大規(guī)模數(shù)據(jù)集上實(shí)現(xiàn)了較好的性能。

表6　Pokerhand和EMNIST（digits）數(shù)據(jù)集上的聚類(lèi)結(jié)果

3.4　參數(shù)分析

對(duì)于無(wú)監(jiān)督學(xué)習(xí)算法，確定最優(yōu)參數(shù)仍然是一個(gè)有待解決的問(wèn)題。為了研究參數(shù)對(duì)LLSC最終聚類(lèi)性能的影響，在實(shí)驗(yàn)中記錄了參數(shù)變化帶來(lái)的不同聚類(lèi)結(jié)果，以分析LLSC對(duì)不同參數(shù)值的敏感性。從實(shí)驗(yàn)結(jié)果中發(fā)現(xiàn)LLSC對(duì)輸入?yún)?shù)非常敏感。圖1為根據(jù)LLSC在不同數(shù)據(jù)集上參數(shù)變化而得到實(shí)驗(yàn)結(jié)果，設(shè)置了不同的橫坐標(biāo)刻度，能夠更加清晰且直觀地分析參數(shù)變化對(duì)算法的影響。如圖1所示，在Tr45數(shù)據(jù)集上，最優(yōu)解的α值為0.8；在MNIST數(shù)據(jù)集上，最優(yōu)解的值為0.5。

圖1　不同數(shù)據(jù)集上不同錨點(diǎn)數(shù)時(shí)α取值在［0.001 100］的實(shí)驗(yàn)結(jié)果

從圖1可見(jiàn)，在Tr45數(shù)據(jù)集和MNIST數(shù)據(jù)上，當(dāng)>10時(shí)，越大，性能指標(biāo)的數(shù)值越小且具有明顯的降低趨勢(shì)；當(dāng)取值太小時(shí)，得到的結(jié)果略遜于最優(yōu)結(jié)果，這可能是取值太小時(shí)迭代的作用變小了。因此，可以得出LLSC不僅對(duì)輸入?yún)?shù)敏感，也對(duì)數(shù)據(jù)集的復(fù)雜度具有極高的依賴性。在一般情況下，的取值應(yīng)在［0.01，10］區(qū)間，尋找不同的數(shù)據(jù)集的最優(yōu)值。由圖1可知，如果采樣錨點(diǎn)數(shù)太小，則所選樣本可能不具有代表性。理論上，更具代表性的錨定將有助于得到更精確的矩陣近似；但是從圖中分析可知，增加參數(shù)并不一定會(huì)獲得代表性的錨點(diǎn)，得到更好聚類(lèi)結(jié)果。這是因?yàn)楫?dāng)增加時(shí)，集群性能有時(shí)會(huì)降低；此外，錨點(diǎn)數(shù)越大，算法所需要的Time會(huì)越長(zhǎng)，為了使矩陣迭代收斂，迭代過(guò)程會(huì)消耗大量的時(shí)間。

4 結(jié)語(yǔ)

本文提出一種融合局部結(jié)構(gòu)學(xué)習(xí)的大規(guī)模子空間聚類(lèi)算法（LLSC），LLSC可以保持較高的聚類(lèi)精度和較低的Time。LLSC首先修改LS2C的目標(biāo)函數(shù)，同時(shí)學(xué)習(xí)全局和局部結(jié)構(gòu)信息；其次通過(guò)非負(fù)拉格朗日松弛方法優(yōu)化目標(biāo)函數(shù)，使用迭代的方法得到最優(yōu)的錨點(diǎn)親和矩陣；最后使用Nystr?m近似方法，通過(guò)較小的樣本子矩陣的特征向量近似Laplacian矩陣的特征向量。在真實(shí)數(shù)據(jù)集上的大量實(shí)驗(yàn)結(jié)果驗(yàn)證了該算法的有效性和效率。未來(lái)，將考慮將LLSC應(yīng)用到圖像檢測(cè)、語(yǔ)音識(shí)別等領(lǐng)域。

[1] ELHAMIFAR E， VIDAL R. Sparse subspace clustering： algorithm， theory， and applications［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013， 35（11）： 2765-2781.

[2] XUE X， ZHANG X， FENG X， et al. Robust subspace clustering based on non-convex low-rank approximation and adaptive kernel［J］. Information Sciences， 2020， 513： 190-205.

[3] ZHAO D， LIU J. Study on network security situation awareness based on particle swarm optimization algorithm［J］. Computers and Industrial Engineering， 2018， 125： 764-775.

[4] LI J， KONG Y， FU Y. Sparse subspace clustering by learning approximation ?0codes［C］// Proceedings of the 31st AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2017： 2189-2195.

[5] ZHENG M， GAO P， ZHANG R， et al. End-to-end object detection with adaptive clustering transformer［C］// Proceedings of the 2021 British Machine Vision Conference. Durham： BMVA Press， 2021： No.709.

[6] LIPOR J， HONG D， TAN Y S， et al. Subspace clustering using ensembles of K-subspaces［J］. Information and Inference： A Journal of the IMA， 2021， 10（1）： 73-107.

[7] HE L， RAY N， GUAN Y， et al. Fast large-scale spectral clustering via explicit feature mapping ［J］. IEEE Transactions on Cybernetics， 2019， 49（3）： 1058-1071.

[8] KANG Z， ZHOU W， ZHAO Z， et al. Large-scale multi-view subspace clustering in linear time［C］// Proceedings of the 34th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2020： 4412-4419.

[9] LIU X， WANG L， ZHANG J， et al. Global and local structure preservation for feature selection ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2014， 25（6）： 1083-1095.

[10] PENG C， ZHANG Z， KANG Z， et al. Nonnegative matrix factorization with local similarity learning［J］. Information Sciences， 2021， 562：325-346.

[11] DING C， HE X， SIMON H D. Nonnegative Lagrangian relaxation of K-means and spectral clustering ［C］// Proceedings of the 2005 European Conference on Machine Learning， LNCS 3720. Berlin： Springer， 2005： 530-538.

[12] FOWLKES C， BELONGIE S， CHUNG F， et al. Spectral grouping using the Nystr?m method［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2004， 26（2）： 214-225.

[13] FRANGELLA Z， TROPP J A， UDELL M. Randomized Nystr?m preconditioning［J］. SIAM Journal on Matrix Analysis and Applications， 2023， 44（2）： 718-752.

[14] HUANG W， YIN M， LI J， et al. Deep clustering via weighted k-subspace network［J］. IEEE Signal Processing Letters， 2019， 26（11）： 1628-1632.

[15] LI J， LIU H， TAO Z， et al. Learnable subspace clustering ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2022， 33（3）：1119-1133.

[16] HUANG S， ZHANG H， PI?URICA A. Sketched sparse subspace clustering for large-scale hyperspectral images ［C］// Proceedings of the 2020 IEEE International Conference on Image Processing. Piscataway： IEEE， 2020： 1766-1770.

[17] ZHOU L， BAI X， ZHANG L， et al. Fast subspace clustering based on the Kronecker product［C］// Proceedings of the 25th International Conference on Pattern Recognition. Piscataway： IEEE， 2021： 1558-1565.

[18] LI J， TAO Z， WU Y， et al. Large-scale subspace clustering by independent distributed and parallel coding［J］. IEEE Transactions on Cybernetics， 2022， 52（9）：9090-9100.

[19] FAN J. Large-scale subspace clustering via k-factorization ［C］// Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York： ACM， 2021： 342-352.

[20] FENG Z， DONG J， GAO X， et al. Subspace representation based on pairwise linear regression for large scale image set classification［C］// Proceedings of the SPIE 12083， 13th International Conference on Graphics and Image Processing. Bellingham， WA： SPIE， 2022： No.1208318.

[21] SI X， YIN Q， ZHAO X， et al. Consistent and diverse multi-view subspace clustering with structure constraint［J］. Pattern Recognition， 2022， 121： No.108196.

[22] XU Y， CHEN S， LI J， et al. Linearity-aware subspace clustering［C］// Proceedings of the 36th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2022： 8770-8778.

[23] WANG Y， WU L， LIN X， et al. Multiview spectral clustering via structured low-rank matrix factorization ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2018， 29（10）： 4833-4843.

[24] 崔藝馨，陳曉東.Spark框架優(yōu)化的大規(guī)模譜聚類(lèi)并行算法［J］. 計(jì)算機(jī)應(yīng)用， 2020， 40（1）： 168-172.（CUI Y X， CHEN X D. Spark framework based optimized large-scale spectral clustering parallel algorithm ［J］. Journal of Computer Applications， 2020， 40（1）： 168-172.）

[25] ZHU X， ZHANG S， LI Y， et al. Low-rank sparse subspace for spectral clustering ［J］. IEEE Transactions on Knowledge and Data Engineering， 2019， 31（8）： 1532-1543.

[26] HU Z， NIE F， WANG R， et al. Multi-view spectral clustering via integrating nonnegative embedding and spectral embedding ［J］. Information Fusion， 2020， 55： 251-259.

[27] WANG C L， NIE F， WANG R， et al. Revisiting fast spectral clustering with anchor graph ［C］// Proceedings of the 2020 IEEE International Conference on Acoustics， Speech， and Signal Processing. Piscataway： IEEE， 2020： 3902-3906.

[28] YANG Y， DENG S， LU J， et al. GraphLSHC： towards large scale spectral hypergraph clustering ［J］. Information Sciences， 2021， 544： 117-134.

[29] ZHAO Z， ZHANG Y， FENG Z. Towards scalable spectral embedding and data visualization via spectral coarsening［C］// Proceedings of the 14th ACM International Conference on Web Search and Data Mining. New York： ACM， 2021： 869-877.

[30] EL HAJJAR S， DORNAIKA F， ABDALLAH F. One-step multi-view spectral clustering with cluster label correlation graph ［J］. Information Sciences， 2022， 592： 97-111.

[31] INOUBLI W， ARIDHI S， MEZNI H， et al. A distributed and incremental algorithm for large-scale graph clustering ［J］. Future Generation Computer Systems， 2022， 134： 334-347.

[32] WANG S， LIU X， LIU L， et al. Highly-efficient incomplete large-scale multi-view clustering with consensus bipartite graph ［C］// Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2022： 9766-9775.

[33] HE W， ZHANG Z， CHEN Y， et al. Structured anchor-inferred graph learning for universal incomplete multi-view clustering ［J］. World Wide Web， 2023， 26（1）： 375-399.

[34] PAATERO P， TAPPER U. Positive matrix factorization： a non-negative factor model with optimal utilization of error estimates of data values ［J］. Environmetrics， 1994， 5（2）： 111-126.

[35] LEE D D， SEUNG H S. Learning the parts of objects by non-negative matrix factorization［J］. Nature， 1999， 401（6755）： 788-791.

[36] LU X， DONG L， YUAN Y. Subspace clustering constrained sparse NMF for hyperspectral unmixing ［J］. IEEE Transactions on Geoscience and Remote Sensing， 2020， 58（5）： 3007-3019.

[37] PENG S， SER W， CHEN B， et al. Robust nonnegative matrix factorization with local coordinate constraint for image clustering［J］. Engineering Applications of Artificial Intelligence， 2020， 88： No.103354.

[38] ZHANG K， ZHAO X， PENG S. Multiple graph regularized semi-supervised nonnegative matrix factorization with adaptive weights for clustering［J］. Engineering Applications of Artificial Intelligence， 2021， 106： No.104499.

[39] PENG C， ZHANG Z， KANG Z， et al. Nonnegative matrix factorization with local similarity learning［J］. Information Sciences， 2021， 562： 325-346.

[40] GILLIS N， HIEN L T K， LEPLAT V， et al. Distributionally robust and multi-objective nonnegative matrix factorization［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2022， 44（8）： 4052-4064.

[41] LEPLAT V， GILLIS N， FéVOTTE C. Multi-resolution beta-divergence NMF for blind spectral unmixing［J］. Signal Processing， 2022， 193： No.108428.

[42] LIU X， SONG P， SHENG C， et al. Robust multi-view non-negative matrix factorization for clustering ［J］. Digital Signal Processing， 2022， 123： No.103447.

[43] FAN D， ZHANG X， KANG W， et al. Video watermarking algorithm based on NSCT， pseudo 3D-DCT and NMF［J］. Sensors， 2022， 22（13）： No.4752.

[44] KANG Z， PENG C， CHENG Q. Twin learning for similarity and clustering： a unified kernel approach ［C］// Proceedings of the 31st AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2017： 2080-2086.

[45] PENG R， SUN H， ZANETTI L. Partitioning well-clustered graphs： spectral clustering works！［C］// Proceedings of the 28th Conference on Learning Theory. New York： JMLR.org， 2015： 1423-1455.

[46] CHEN X， CAI D. Large scale spectral clustering with landmark-based representation ［C］// Proceedings of the 25th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2011： 313-318.

[47] KANG Z， LIN Z， ZHU X， et al. Structured graph learning for scalable subspace clustering： from single view to multiview ［J］. IEEE Transactions on Cybernetics， 2022， 52（9）： 8976-8986.

[48] CHEN X， HONG W， NIE F， et al. Spectral clustering of large-scale data by directly solving normalized cut ［C］// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2018： 1206-1215.

[49] NIE F， WANG C L， LI X. K-multiple-means： a multiple-means clustering method with specified k clusters ［C］// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2019： 959-967.

[50] CAI D， CHEN X. Large scale spectral clustering via landmark-based sparse representation［J］. IEEE Transactions on Cybernetics， 2015， 45（8）： 1669-1680.

[51] PENG X， TANG H， ZHANG L， et al. A unified framework for representation-based subspace clustering of out-of-sample and large-scale data ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2016， 27（12）： 2499-2512.

Large-scale subspace clustering algorithm with Local structure learning

REN Qize， JIA Hongjie*， CHEN Dongyu

（，，212013，）

The conventional large-scale subspace clustering methods ignore the local structure that prevails among the data when computing the anchor affinity matrix， and have large error when calculating the approximate eigenvectors of the Laplacian matrix， which is not conducive to data clustering. Aiming at the above problems， a Large-scale Subspace Clustering algorithm with Local structure learning （LLSC） was proposed. In the proposed algorithm， the local structure learning was embedded into the learning of anchor affinity matrix， which was able to comprehensively use global and local information to mine the subspace structure of data. In addition， inspired by Nonnegative Matrix Factorization （NMF）， an iterative optimization method was designed to simplify the solution of anchor affinity matrix. Then， the mathematical relationship between the anchor affinity matrix and the Laplacian matrix was established according to the Nystr?m approximation method， and the calculation method of the eigenvectors of the Laplacian matrix was modified to improve the clustering performance. Compared to LMVSC （Large-scale Multi-View Subspace Clustering）， SLSR （Scalable Least Square Regression）， LSC-k （Landmark-based Spectral Clustering using k-means）， and k-FSC（k-Factorization Subspace Clustering）， LLSC demonstrates significant improvements on four widely used large-scale datasets. Specifically， on the Pokerhand dataset， the accuracy of LLSC is 28.18 points percentage higher than that of k-FSC. These results confirm the effectiveness of LLSC.

subspace clustering; local structure learning; Nonnegative Matrix Factorization (NMF); large-scale clustering; low-rank approximation

This work is partially supported by National Natural Science Foundation of China （61906077）.

REN Qize， born in 1997， M. S. candidate. His research interests include large-scale subspace clustering.

JIA Hongjie， born in 1988， Ph. D.， associate professor. His research interests include clustering， machine learning.

CHEN Dongyu， born in 2000. His research interests include subspace clustering.

TP181； TP311.13

A

1001-9081（2023）12-3747-08

10.11772/j.issn.1001-9081.2022111750

2022?11?24；

2023?04?30；

2023?05?12。

國(guó)家自然科學(xué)基金資助項(xiàng)目（61906077）。

任奇澤（1997—），男，河南許昌人，碩士研究生，主要研究方向：大規(guī)模子空間聚類(lèi)；賈洪杰（1988—），男，河北衡水人，副教授，博士，CCF會(huì)員，主要研究方向：聚類(lèi)、機(jī)器學(xué)習(xí)；陳東宇（2000—），男，廣西柳州人，主要研究方向：子空間聚類(lèi)。