超聲波振動農業觸土部件變幅桿性能分析與試驗

趙智豪,王家勝,楊麗麗

(青島農業大學 機電工程學院,山東 青島 266109)

0 引言

土壤耕作、深松等觸土作業是農業生產中耗能最大的環節,降低觸土部件阻力,不僅節能減排[1],還可降低對大功率動力裝備的要求,從而減輕對土壤的壓實破壞[2]。研究表明:頻率小于30Hz的振動觸土部件是降低阻力的一種有效手段,但是由于振動耗能導致總能耗通常都會大于非振動觸土部件[3-4],且振動引起關聯部件或整機振動降低了部件的壽命,而利用高頻低幅振動觸土部件作業是解決以上問題的有效手段。其中,超聲波是頻率超過20kHz的高頻振動,目前在金屬、橡膠等材料的輔助切削應用研究中表現出更優的切削表面質量以及更低的切削阻力[5-7]。Bo Liu通過室內試驗研究超聲波振動直刃鏟刀垂直切削圓柱土樣發現,阻力降低率超過50%[8]。王家勝等研究發現:超聲波振動輔助可以有效地降低觸土部件進行土壤切削挖掘時的阻力,且具有更強的碎土效果[9]。

變幅桿是超聲波振動觸土部件系統的核心部件之一,本文通過理論分析并結合仿真與試驗的方法,研究不同類型變幅桿對超聲振動觸土部件工作振幅放大效果以及整體諧振影響關系,旨在為高頻振動農機觸土部件的最佳諧振匹配提供理論和技術支撐。

1 超聲變幅桿理論分析與設計

1.1 超聲波振動觸土部件結構原理

超聲波振動土壤切削挖掘裝置的結構原理如圖1所示。

圖1 超聲波振動觸土部件裝置Fig.1 Ultrasonic vibration oil-engaging component device

工作時,超聲波發生器將交流電信號轉換為20kHz以上高頻電信號,經夾心式換能器的逆壓電效應將高頻電信號轉換為高頻機械波。此時高頻機械波的振幅非常小,利用變幅桿兩端截面積大小不同的特性可實現能量的聚集,從而將傳遞而來的微小振幅的機械振動進行聚集放大[10-11],并將放大的振動傳遞給挖掘鏟,實現高頻振動。

1.2 變幅桿振動理論模型

為方便計算,設計過程中一般將變幅桿看作1根各向均勻且材料特性相同的變截面桿。根據牛頓定律,作用在變截面桿一個微小單元上的動力學方程為

(1)

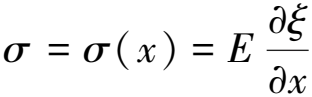
簡諧振動的狀態下,式(1)又可寫為[10-11]

(2)

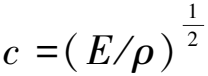
單一形變幅桿根據加工形狀不同分可分為指數型、懸鏈型、圓錐型和階梯型,其結構如圖2所示。

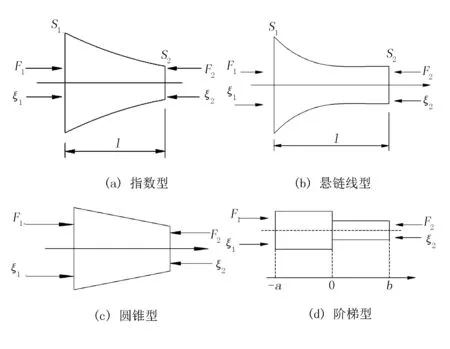
圖2 不同形狀變幅桿結構圖Fig.2 Design diagram of different shapes of variation rods

根據4種變幅桿的截面積函數求解式(2),可得到不同型號變幅桿的位移函數和應變分布函數[12]。

1)指數型變幅桿軸向位移為

(3)

軸向應變分布為

(4)

2)懸鏈線型變幅桿軸向位移為

(5)

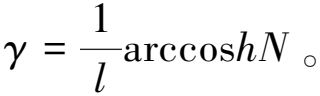
軸向應變分布為

(6)

3)圓錐形變幅桿軸向位移為

(7)

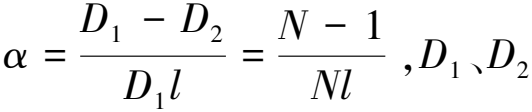
軸向應變分布為

(8)

4)階梯型變幅桿軸向位移為

(9)

軸向應變分布為

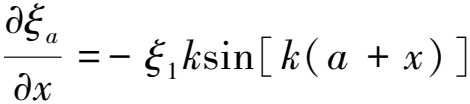
(10)

1.3 變幅桿參數計算與軸向位移、應變分布特征

反映變幅桿性能的主要參數如下:

1)諧振頻率f和諧振長度Ip。當超聲波振動傳遞到變幅桿時,為減少能量因結構自身的損失,最大限度地放大由換能器傳遞來的振幅,應使所設計的變幅桿固有頻率與施加振動頻率近似相等,達到最佳諧振狀態,輸出最大振幅。此時,變幅桿的工作頻率為諧振頻率,對應所設計的變幅桿長度為諧振長度。

2)放大系數Mp。指變幅桿工作過程中輸出端(小端)振幅與輸入端(大端)振幅的正比值。

3)形狀因數φ。無量綱常數,只受到變幅桿形狀的影響,是為了確定變幅桿發生振動時可以達到的最大振動速度;不同變幅桿的形狀因數越大,在相同工作條件下輸出端所能達到的最大振動速度也就越大。

4)位移節點x0。在超聲振動工作過程中,位置始終保持不變的點為位移節點。

表1 變幅桿關鍵參數設計計算結果

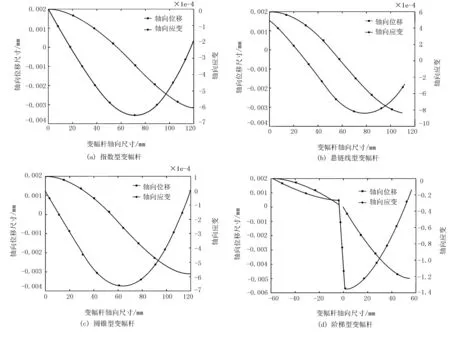
圖3 節點位移和軸向應變分布圖Fig.3 Nodal displacement and axial strain distribution diagram

由軸向位移分布圖可知:4種變幅桿的最大位移都發生在變幅桿的小端處,且圖中軸向位移尺寸為0的點對應的橫坐標即為變幅桿的位移節點,放大系數和位移節點的值都與表1中的計算結果一致;軸向應變分布曲線的最低點即為最易發生破壞失效變幅桿的極大應變點。

結合分布圖與計算結果可知:當變幅桿的截面系數相同時,如果面積系數N的值較小,則階梯型變幅桿的放大系數最大,其次是懸鏈線型、指數型,最小的是圓錐型變幅桿;指數型和圓錐型變幅桿的諧振長度l隨N的增大而增大。由于在深松、根莖類作物收獲等觸土作業環境都需要大功率牽引,因此在超聲高頻振動輔助土壤切削挖掘環境下變幅桿輸出端需要提供較大的振幅,則需要較大疲勞強度的變幅桿材料來保證部件的耐久性。但是,不同形狀變幅桿不同位置的周期性應變也會影響復雜工作環境下的耐久性。所以,在合理設計的前提下,應該選擇形狀因數較大形狀的變幅桿。階梯型變幅桿雖然放大系數較大,但形狀因數最小,最容易遭到破壞。圓錐型變幅桿的形狀因數最大,其它兩種居中。

2 有限元分析及優化

2.1 模態分析

為驗證所設計4種變幅桿的合理性,對其進行模態分析,確保超聲波振動挖掘鏟工作時能達到諧振頻率。利用SolidWorks進行變幅桿建模,再導入Workbench中進行分析,將超聲波變幅桿三維模型導入到Workbench中,對模型網格劃分后進行前10階模態分析。結果表明:指數型、懸鏈線型、圓錐型在第7階模態及階梯型在第8階模態的頻率最接近20kHz,且均為軸向振動,結果如表2所示。通過比較發現:懸鏈線型變幅桿有限元模態分析與解析值相對偏差較大,達到12.4%,主要是因為該類變幅桿的形狀函數與實際模型形狀差異導致;另外3種形態的變幅桿的模態有限元模態分析值與解析值相差不大。

表2 各種形狀變幅桿固有頻率比較

圖4為所設計變幅桿模態分析后在各自固有頻率下的形變圖。由圖4可以看出:理論分析時所得的位移節點為中間零位移處,變幅桿最大位移發生在小端部分處,與MatLab分析結果一致。

2.2 諧響應分析

將4種變幅桿三維模型載入Workbench后采用Full法對變幅桿進行諧響應分析。在變幅桿大端(輸入端)面節點上施加頻率范圍為19～21kHz、振幅為1μm的振動激勵。

由諧響應分析得到變幅桿固有頻率下的軸向位移分布。在Workbench中,標記所分析變幅桿中心線上的各個節點,然后得出其軸向位移,在末端的節點位移與大端面上的節點位移之比就是變幅桿的放大系數。分析結果如圖5所示。

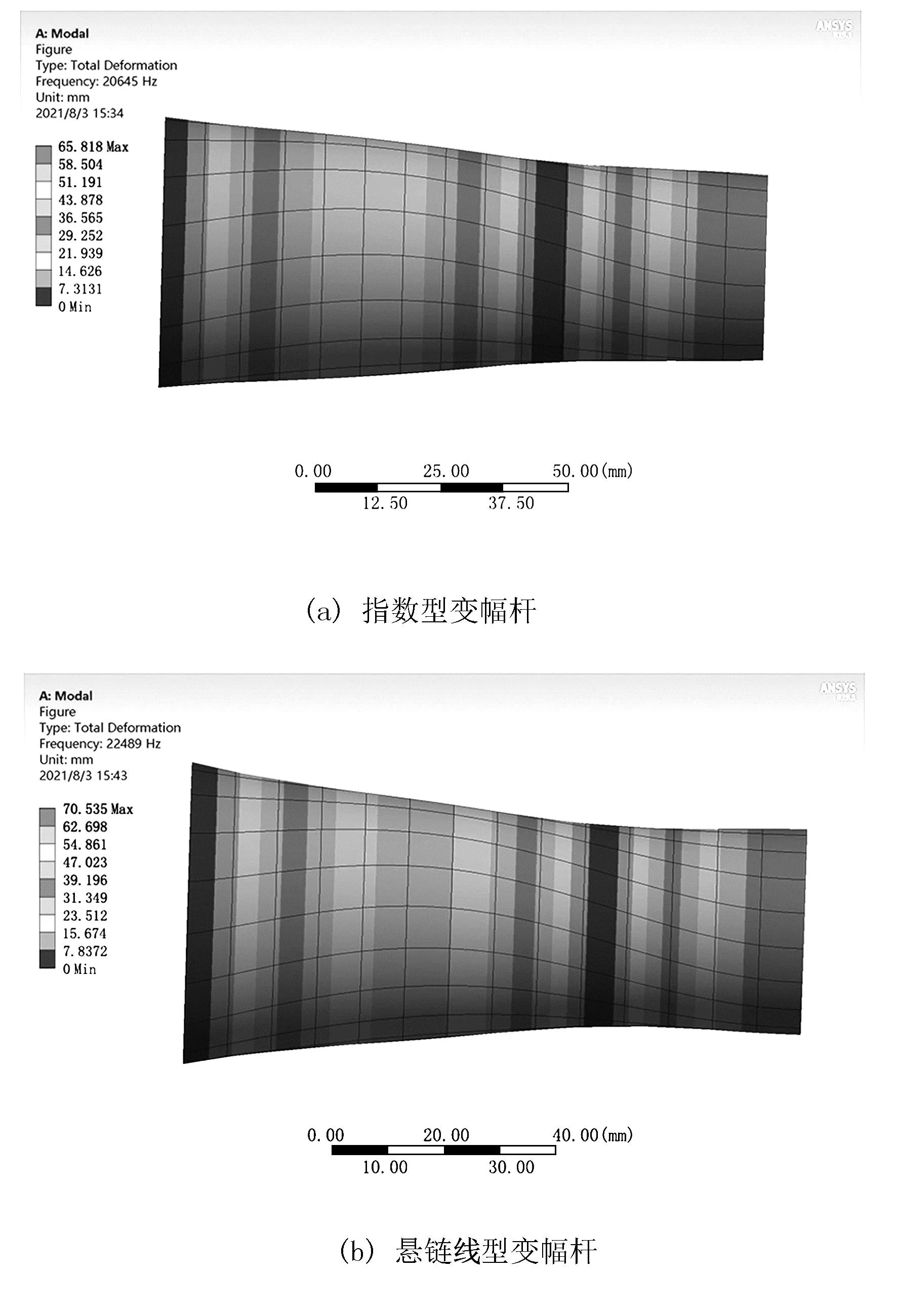
圖4 變幅桿形變圖Fig.4 Variable rod deformation diagram

圖5 變幅桿仿真分析圖Fig.5 Simulation analysis diagram of the variable amplitude rod

根據仿真結果獲得放大系數與解析解比較如表3所示。通過比較可知:仿真得到的軸向位移與預先設計結果相近,且節點位移與MatLab的計算結果基本相同,位移放大系數也與仿真云圖分布基本相同,整體具有良好的一致性。

表3 變幅桿仿真分析結果

3 試驗驗證

3.1 試驗設備與儀器

自制超聲波振動觸土部件試驗測試系統由超聲波發生器、換能器、變幅桿、挖掘鏟、激光位移傳感器及計算機等組成,如圖6所示。其中,挖掘鏟的振幅響應信號由松下HL-G105-A-C5激光位移傳感器進行采集,分辨率為0.5μm/s,經過模數轉換器將數據輸出到計算機軟件系統進行數據分析和處理。

圖6 超聲波振動觸土部件試驗測試系統Fig.6 Test system for ultrasonic vibration soil-engagement component

3.2 試驗方案

試驗目的是為了驗證4種變幅桿的振動響應特性,試驗指標為挖掘鏟響應振幅A。試驗水平為4種類型變幅桿和19.5～21kHz范圍的超聲波激振頻率。因素水平編碼如表4所示。

表4 試驗因素水平編碼

試驗取4個水平、2個因素,故進行16組全部試驗,方案與結果如表5所示。圖7為4種不同類型變幅桿在19.5～21kHz激振頻率下的挖掘鏟振幅變化曲線。由圖7可以看出:經變幅桿放大的機械振動在其固有頻率(20～20.5kHz)附近都能達到各自的最大振幅,挖掘鏟振幅響應由大到小順序為階梯型(2.9μm)>指數型(2.3μm)>圓錐型(2.2μm)>懸鏈線型(2.1μm),與計算仿真分析結果基本相同。

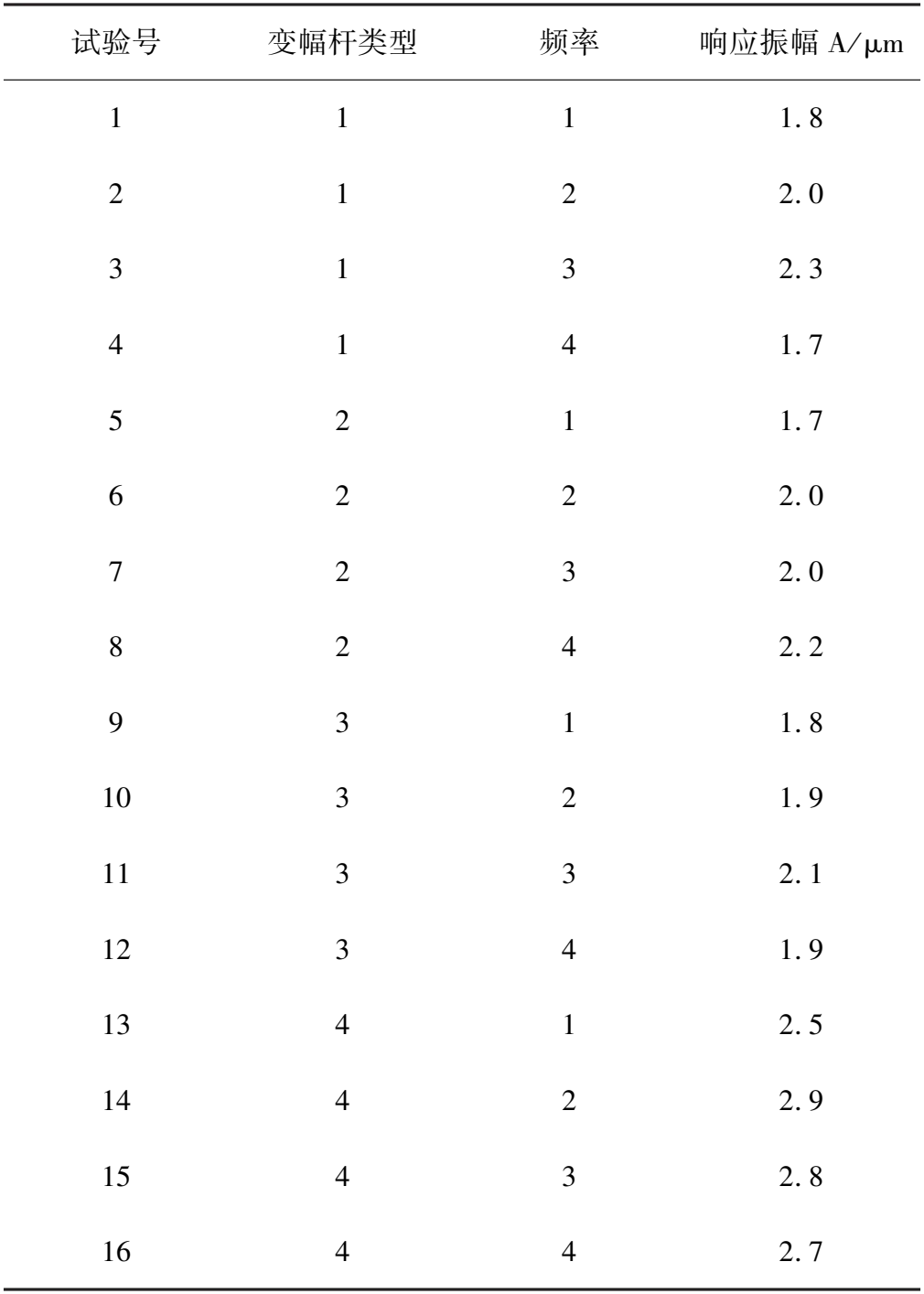
表5 超聲變幅桿實驗方案與結果

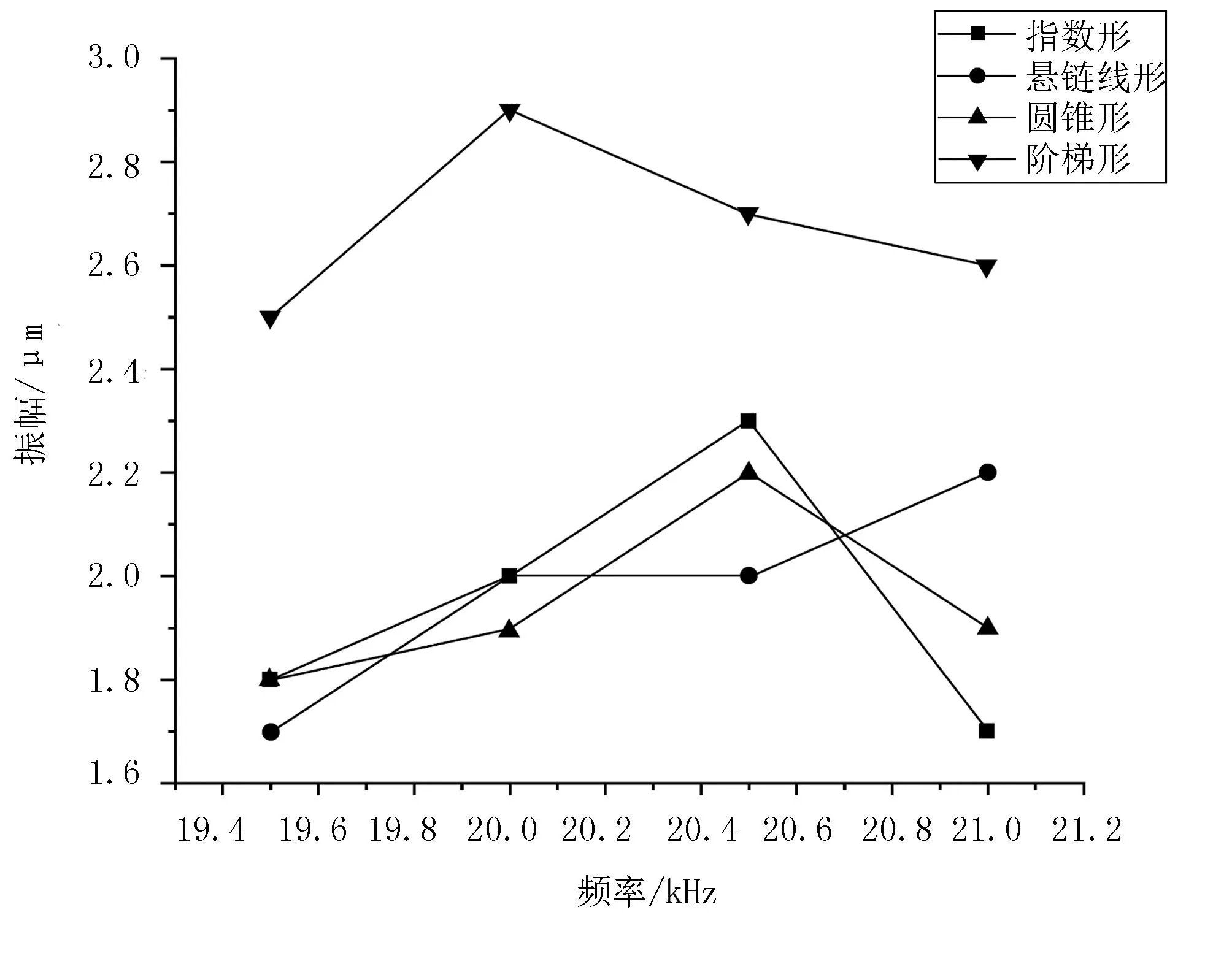
圖7 變幅桿頻率-挖掘鏟振幅關系曲線Fig.7 Relation curves between variable amplitude rod frequency - shovel amplitude

4 結論

針對超聲波振動觸土部件的結構要求,通過理論分析并結合仿真與試驗的方法,對比研究了指數型、懸鏈型、圓錐型和階梯型4種不同類型超聲波變幅桿的諧振效應和聚能放大性能。研究結果表明:4種變幅桿的最大位移都發生在變幅桿的小端處;相同條件下,變幅桿放大系數從大到小依次為階梯型、懸鏈線型、指數型和圓錐型;階梯型變幅桿雖然放大系數較大,但形狀因數最小,最容易遭到破壞;圓錐型變幅桿的形狀因數最大,其它兩種居中。