借助整體思想方法 助力數學解題教學
曹如祥
(福建省上杭縣第一中學,福建 龍巖 364200)
整體思想方法是基于問題整體視角切入,突出對問題整體結構的分析與改造,找到問題的整體結構特征,善于采用“集成”的眼光,將問題中的某些式子或者圖形看作是一個整體,把握好彼此之間的聯系,有意識、有目的地進行整體處理,從而找到簡便的解題思路與方法.在高中數學解題教學中,教師應充分借助整體思想方法的優勢,助力學生采用整體思想分析題意,使其快速、精準地找到解題切入點,降低試題難度,驅使他們輕松、高效地解題[1].
1 借助整體代入方法,助力數學解題教學
例1 已知函數f(x)=ax3+bsinx+2,f(-1)=10,那么f(1)的值是什么?
分析本題既可以使用常規方法,也可以采用整體代入的方法.當難以從已知條件中找到題設的未知量,無法發現條件與題設之間的關系時,采取整體代入法可以把題設中的未知量用其它含有未知量的式子來代替,最終達到消元求解的目的.
解法1 根據f(-1)=10可以得到
f(-1)=a(-1)3+bsin(-1)+2=10.
即-(a×13+bsin1)+2=10.
則a×13+bsin1=-8.
所以f(1)=a×13+bsin1+2=-6.
解法2 可設φ(x)=ax3+bsinx,則
f(x)=φ(x)+2.
根據題意可知φ(x)是奇函數,
根據f(-1)=10能夠得到
f(-1)=φ(-1)+2=10.
所以φ(-1)=8.所以φ(1)=-8.
所以f(1)=φ(1)+2=-8+2=-6.
2 借助整體換元方法,助力數學解題教學

分析解答這道題目時可使用整體換元法,將所求△AQB面積的最大值問題變得簡單化,轉變成一個求二次函數最值類的問題,最終順利求出△AQB面積的最大值.

(1+4k2)x2+8kmx+4m2-16=0.
根據△1>0可得m2<4+16k2.

①
結合韋達定理可得





②
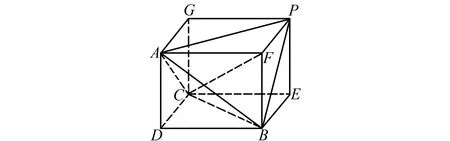
即0 例3已知數列{an}的通項公式an=(2n-1)xn(x≠1),那么該數列的前n項和Sn是什么? 分析處理這道題目時,可以直接在數列的和式左右兩邊同時乘以x,再采用錯位相減的方式,求出數列前n項和Sn的表達式,結合整體思想把代數式進行變形,使之呈現出某種規律,然后進行整體運算,達到減少運算的目的. 解析數列{an}的前n項和 Sn=x+3x2+5x3+…+(2n-1)xn. ③ 將③式兩邊同乘以x整體變形后得 xSn=x2+3x3+5x4+…+(2n-1)xn+1. ④ ③-④,得 例5 求值sin10°sin30°sin50°sin70°. 分析本題題干十分簡單,如果直接計算學生往往無從下手,此時教師可提醒他們采用整體設元的方法,設出新的方程,再結合正弦的二倍角公式把非特殊角的三角函數轉變成特殊角的三角函數,從而輕松求得答案. 分析解答本題時,教師可以帶領學生基于三角函數的相關公式展開整體思考,使其將已知條件作為整體進行構造和計算,不僅可以減少計算步驟,還降低解題難度,這也是處理此類問題的最佳方案. 解析根據題干中提供的已知條件得 例7 如圖1所示,已知三棱錐P-ABC的三組對棱相等,其中PA=13,PB=14,PC=15,那么該三棱錐的體積多少? 圖1 三棱錐P-ABC 分析處理這一題目時,由于題目中給出三棱錐的三組對棱相等,可以聯想到長方體的對角線,于是教師可以引導學生使用整體補形的方法進行解題,使其結合三棱錐的特征,通過添加輔助線的方式把該三棱錐補充成一個如圖2所示的長方體CDBE-GAFP,問題也就迎刃而解. 圖2 由三棱錐P-ABC構成的長方體CDBE-GAFP 解析根據題意將三棱錐P-ABC補充成一個長方體CDBE-GAFP,則三棱錐的三條棱分別是長方體的面的對角線. 設AD=a,DB=b,DC=c,由此能夠得到 a2+b2=152, b2+c2=132, a2+c2=142. 把這三個式子聯立得到一個方程組,解之得 則VP-ABC=VCDBE-GAFP-4VA-BCD 總的來說,在高中數學教學實踐中,解題訓練既是一個常規環節,又是重要構成部分.常用的解題方法有很多,教師除帶領學生掌握一些基本解題方法以外,還要注重整體思想方法的應用,充分借助整體思想方法的優勢,根據實際解題需求靈活采用整體代入、換元、運算、設元、構造、補形等多種方法,使其優化解題過程,全力提高解題效率[2].
3 借助整體運算方法,助力數學解題教學


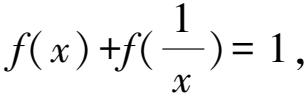

4 借助整體設元方法,助力數學解題教學

5 借助整體構造方法,助力數學解題教學


6 借助整體補形方法,助力數學解題教學