圓錐曲線的幾何性質在解題中的應用研究
鄒慧妤
(福建省龍巖市第二中學,福建 龍巖 364000)
圓錐曲線不僅是高中數學教學中的重點知識,還是一大難點.學生通過對圓錐曲線相關知識的學習,可以有效培養自身的邏輯思維、計算推理、數形分析、空間轉換與想象等多項能力,還有助于學生轉化思想、完整思維與樂觀心態的形成.在高中數學解題教學中,教師需指導學生應用圓錐曲線的幾何性質處理部分特殊試題,使其根據題意靈活運用圓、拋物線、雙曲線、橢圓等相關知識來解題,助推他們順利突破解題障礙,不斷提升個人的解題水平.
1 運用圓錐曲線定義,有效解答數學最值問題
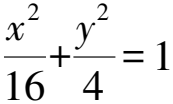
解析當讀完題目內容以后,教師要求學生把圓錐曲線的定義、最值等基礎知識羅列出來,結合現有現象研究本題所考查的知識要點.圍繞題干中提供的兩個條件,他們可采用橢圓的第一定義與不等式的基本性質等知識,把原題轉變為求點D與兩個焦點的距離積問題,據此求解[1].

由于只有當|DF1|=|DF2|時,等號才能夠成立,根據題意是求點D距橢圓兩個焦點的距離之積A的最大值,所以當|DF1|=|DF2|時距離之積的最大值是16,所以點D的坐標是(0,2)或者(0,-2).
本題主要考查學生對圓錐曲線定義的具體應用.通過分析題目能明確這一點,但是需注重對圓錐曲線定義的拆分,使學生快速掌握解題思路,提高解題效率.
2 借助數形結合思想,解決動直線過定點問題
動直線過定點問題是高中數學中一類難度比較大的題目,既考查學生對圓錐曲線相關幾何性質的應用,又對學生的數學分析能力有著較高要求.教師可提示學生借助數形結合思想的優勢,深化個人邏輯思維,使其快速找到解題的切入點.

解析本題是一道典型的動直線過定點問題,結合題干中給出的信息讓學生進行梳理,發現點A不僅在l1上,還在l2上,l1和l2又是垂直關系,所以與斜率肯定有所聯系,學生從斜率著手幾何恒等關系列出相關方程來解決.
設直線l1的斜率是k,根據題意可知l1過定點A(0,1),則直線l1的方程是y=kx+1.



圖1 例2題圖
3 幾何性質入手分析,驅使學生簡潔解答試題
在一些解析幾何類試題中往往含有一定的幾何圖形結構,教師應當引領學生從圓錐曲線的幾何性質入手分析題意,認真審理題目內容,找出各個條件及條件之間的聯系,使其從中迅速找到解題思路,驅使學生簡潔解答試題.

解析學生通過對題目內容的閱讀與分析,可以根據題意畫出圖形,如圖2所示,根據正弦定理求sin∠AFB值,然后根據圖形結構求出a與c的值.
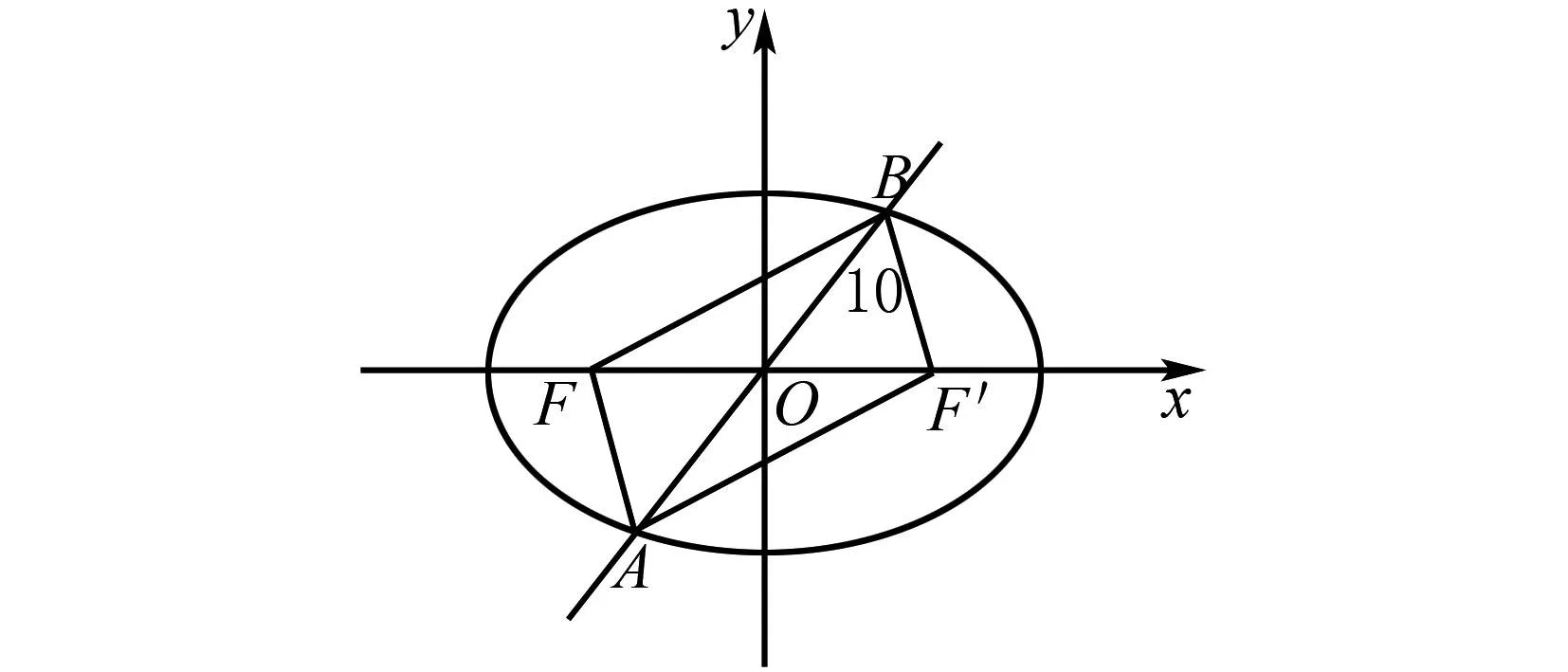
圖2 例3題圖
由此可知sin∠AFB=1,則∠AFB=90°,那么在Rt△ABF中,BF2=AB2-AF2=102-62=64,所以|BF|=8.
設F′是該橢圓的右焦點,那么四邊形AFBF′是矩形,|BF′|=|AF|=6.
所以2a=6+8=14,解得a=7.

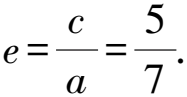
4 注重融入相關知識,有效降低學生解題難度
數學是一門典型的邏輯性科目,各個知識點之間有著關聯性較強的特點,尤其是在解題訓練中,在處理一些數學題目時往往要用到與之有關的知識.要求學生閱讀題目內容時,深入發掘題目中涉及的知識點,找到這些知識之間的內在聯系,使其形成清晰、簡便的解題思路,有效降低解題難度.
解析大部分學生看到這一題目時,一般都能夠明確解題的大致方向,即采用坐標求解矩形面積.不過由于受到思維的限制,導致他們習慣性把坐標設為x與y,這樣后續計算量較大,十分麻煩.結合題意發現求解這一最值時要用到函數知識,其中三角函數是一種有界函數,能夠提供很好的助力,可聯系三角函數及圓錐曲線的幾何性質進行解題.

5 巧妙利用幾何性質,解答軌跡類型問題
在軌跡類型題目中,圓錐曲線主要表現在兩個方面,即根據方程對動點運動軌跡進行判斷、利用圓錐曲線性質求解方程式.軌跡類型題目主要考查學生對曲線性質的掌握以及運用,靈活利用曲線性質對運動軌跡進行分析,列出相應的方程式[2].
例5 方程x2+(y-2)2=x-y-4對應點P(x,y)的軌跡是____.
A.橢圓 B.拋物線 C.雙曲線 D.兩直線
解析在解題時,通過對方程進行變形,可以看出動點P(x,y)到定點F(0,2)的距離與其到直線l:x-y-4=0的距離的比值是2,根據曲線的性質可以得出,離心率大于1的只有雙曲線,所以點P的運動軌跡是雙曲線.
6 靈活利用曲線性質,有效解決三角形問題
在高考數學中,圓錐曲線與三角形結合是高考命題的一個重要趨勢,要求學生利用曲線性質,結合已知條件做出判斷,構建圓錐曲線與三角形的關系,完成三角形問題解題.
例6已知橢圓的兩個焦點分別是F1,F2,經過點F2作出橢圓長軸的垂線,和橢圓的一個交點是P,如果△F1PF2為等腰直角三角形,則橢圓的離心率是____.
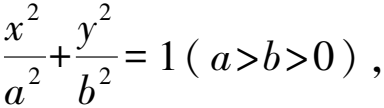
根據題意得知∠F1PF2=90°,∠PF1F2=45°.

總而言之,圓錐曲線是一類極為重要的數學知識,在整個高中數學課程體系中占據著非常關鍵的位置,而圓錐曲線的幾何性質不僅有著自身的特殊性,還能夠應用到解題中.數學教師在解題訓練中,應當指引學生根據實際情況有的放矢地運用圓錐曲線的幾何性質,使其形成清晰的解題思路,找到更為便捷的解題方法,繼而提高他們的數學解題能力.

