新課標背景下小升初銜接(數學)的思考與探索
林淑金
(福建省漳州市第三中學,福建 漳州 363000)
基金項目:本文系福建省教育科學“十四五”規劃2022年度課題“新課標背景下初中數學大單元整體作業設計體系的構建與實踐”的研究成果(立項批準號:FJJKZX22-358)
數學這個學科一直廣受大家的重視,也被認為是最重要的一門科學.不僅是因為數學在升學考試中起著重要的作用, 還因為數學是為人們提供認識與探索現實世界的觀察方法,通過數學的眼光認識世界,再用數學的思維思考現實世界,最后用數學的語言表達現實世界,進而解決現實問題,具有現實的意義與價值.
九年義務教育從知識本身和核心素養方面都具有整體性、一致性和階段性的特點.從小學數學過渡到初中數學,哪些知識是小學學過的,初中還要學習?為什么還要學?哪些知識是小學沒有學過的,初中才學習?高中是不是還要學習?家長和教師們不僅要弄清楚小學和初中的數學知識體系,還要弄明白這兩個知識體系之間的關系,更要弄明白在不同的學段核心素養的不同表現形式.文章基于研究《義務教育數學課程標準(2022年版)》(以下簡稱《新課標》)[1]的背景下,充分考慮當今學生學習心理特征的前提下,指導學生在初中階段養成可持續發展、行之有效的學習方法,為高中學習甚至更高年級的學習深造打下堅實的基礎.
1 課程內容上的銜接
義務教育階段數學課程由數與代數、圖形與幾何、統計與概率、綜合與實踐四個學習領域組成.根據不同學段目標和不同學情,四個學習領域的內容有所不同,詳見表1.
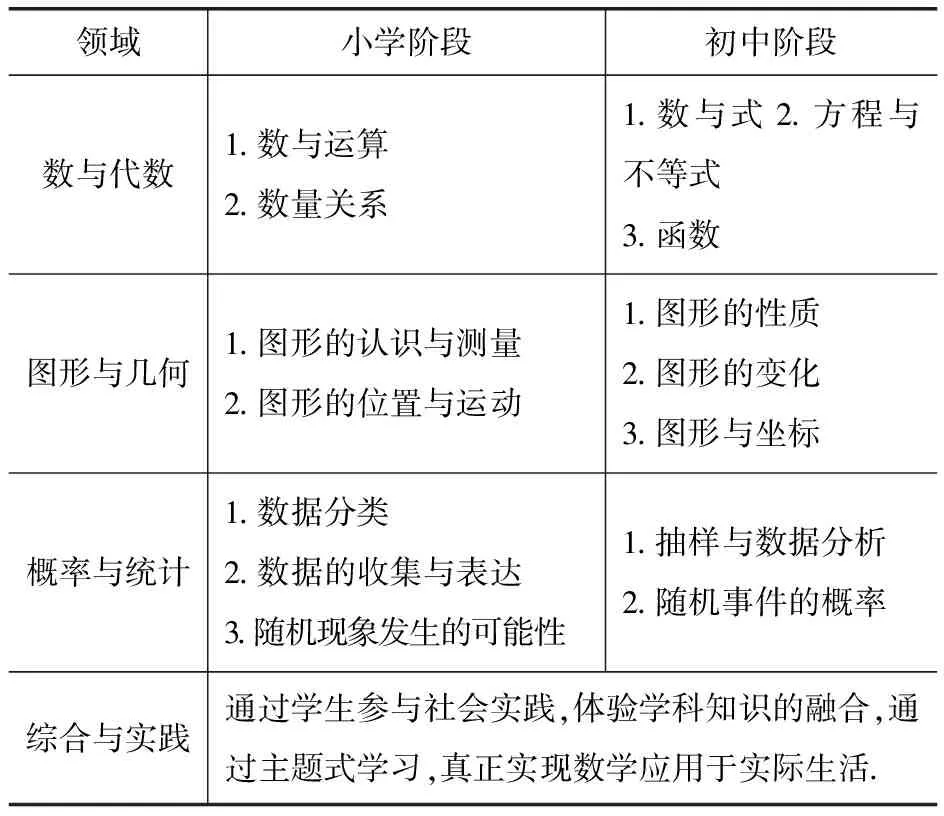
表1 各學段各領域的主題
在課程內容上,小學數學與初中數學具有一定的一致性,小學階段的“數與運算”“數量關系”的學習是對數的相關概念的理解和運算,這一知識是初中學習“數與式”的基礎;小學階段學習的“圖形和幾何”“概率與統計”的相關知識為初中學習“圖形的性質”“概率與統計”積累一定的經驗方法.小學數學教學主要側重于學生的基本運算能力訓練,主要目的是激發學生的數學興趣.在初中數學教學中,學生會接觸到幾何、代數等內容,其中包含了更多邏輯推理性的數學學習內容,數學學習難度大大提升,課程內容存在的差異給中小學數學學習的銜接教學帶來挑戰[2].
在課程內容上,小升初銜接不僅要弄清楚小學部分所學內容對初中數學知識的影響,更要引導學生在復雜的數學知識中建立數學體系,理清數學知識框架.例如“關于數”,小學階段學習了很多關于數的名詞:自然數、整數、負數、分數、小數、帶分數、假分數、奇數、偶數、質數、合數、倒數、相反數……這些表示不同意義的數之間有什么關系?每個數產生的背景和現實需要是什么?事實上可以將小學階段學的這么多不同定義的數分為以下三類:(1)自然數、整數、分數、有理數、無理數、實數、復數……每個名詞都代表了一種數的范圍.隨著學習的深入,我們所學的數域因為解決現實問題的需要在不斷擴大;(2)奇數、偶數、質數、合數、2的倍數、3的倍數、4的倍數、5的倍數、8的倍數……每個名詞都代表具有某個特殊特征的數,也隱含著數的分解,整除等相關概念;(3)倒數、相反數、因數、倍數……每個名詞都代表了兩個數之間的一種數量關系.這些不同概念的數的產生背景和現實需要可以用圖1簡明表達:

繩結記事
課程內容上的銜接不是小學知識的復讀,而是小學知識的整合.在初一年級剛開學的一兩周內做好小升初銜接,教師要引導學生將六年所學的知識串聯成一張知識大網,搭建知識的框架,有了這張牢固的大網才能承受更多的知識.
2 核心素養上的銜接
數學課程的最終目的是培養學生的數學核心素養.數學核心素養具有總體性、承接性和階段性的特點,在不同的階段根據不同的學情有不同的體現.小學階段側重動手能力,注重對經驗的感悟,初中階段側重對概念產生過程的理解,注重合情推理到演繹推理的過程獲得.核心素養在小學和初中階段的主要表現見表2.

表2 核心素養在不同學段的主要表現
對照這個表格可以很清楚地認識哪些核心素養是小學和初中學段都需要的,在小升初銜接階段應該側重對計算能力、幾何直觀,應用意識和推理能力的培養.以九宮格幻方綜合實踐課為例,小學階段鼓勵孩子多試多練,計算驗證,提煉經驗.初中銜接階段可以引導學生實驗+觀察+抽象歸納+演繹推理.九宮格幻方要求九個格子里不重復地填下1~9這九個數字,并要求每條線上的數字之和相等,這個和稱為幻和.可以引導學生探究如下問題:問題(1)幻和怎么定?幻和是多少?(2)中間數怎么確定?中間數是多少?(3)斜線上的數怎么定?(4)總的有幾種填法?(5)幻方的本質是什么?可以和孩子一起尋求解答.(1)9個數字之和為45,設幻和為w,每個幻和包括3個數字,從三個縱列看(如圖2),則3w=45,求得幻和w=15.(2)對角兩條線和橫縱兩條線可以得到12數字之和為4個幻和,即4*15=60,這12個數字其中中間數重復出現了4次(如圖3),因此中間數=(60-45)÷3=5.(3)同一條線上的和為15,因此構成數對.有偶數數對2和8、4和6;奇數數對1和9、3和7.同一數對排在同一條線上.奇數15=奇數+偶數+偶數,奇數15=奇數+奇數+奇數,可以得到偶數對在斜線上.(4)2和8、4和6數對放在斜線上,分類討論,共8種填法.(5)古人歸納出來的:九宮之義,法以靈龜,二四為肩,六八為足,左三右七,戴九履一,五居中央.現在看來多么的形象啊(第一種填法).而其他種填法可以形象地看成是一只靈龜在繞中心旋轉或是翻身(對稱).因此幻方的本質是旋轉,是對稱,更是數學思維.通過研究幻方可以鍛煉學生的計算能力,發展思維,提高抽象能力和推理能力.利用暑假或是新學年剛開學比較輕松的時間研究數學相關的游戲,在玩中學,在學中玩,不失為一種非常好的銜接方法.
新課標提出課程目標要以學生發展為本,以核心素養為導向,強調學生獲得知識的情感和體驗,注重學生運用數學知識和方法,提高“發現、提出、分析和解決問題”的能力.核心素養的養成是一個漫長的過程,來不得一點功利性,所以銜接課堂要舍得在綜合實踐活動課上投入時間和精力,在綜合與實踐的領域多做研究和探索.
3 學習方法上的銜接
隨著義務教育改革的持續推進,新課程指導綱要從以往重視教師“教”的角色,逐漸向重視學生“學”的角度進行變革,更加凸顯了學生的主體作用[2],每個孩子都是鮮活的個體,每個孩子的思維都不太一樣.現在的課堂教學大多數仍是大班化教學,在小學階段為了維持好的課堂紀律,有些教師甚至連學生的坐姿都有統一的規定,該做哪些筆記,筆記寫在哪里都有統一的要求,這樣的教學模式顯然很不利學生個性化思維的培養.在初中階段如何讓每個孩子的思維得到充分的發展,這不僅考驗教師的功力,更要求孩子在暑假或在初中新學期培養適合自己思維發展的學習方法.
(1)在小升初銜接階段請人提前將新課的內容教一遍,這樣的做法筆者認為是很不恰當的.建議可以利用各種教學資源自行預習新課,這樣可以讓學生對新知識保持強烈的好奇心,在很大程度上會提高孩子上課的聽課專注度.
(2)教師要鼓勵學生大膽質疑,預習每節新課時引導學生提出1~2個問題,如果這個問題可以及時得到解答,那自然最好,如果不能及時得到解答,那么帶著問題來聽課,效果更佳.每個問題的提出都是學生思維的深層次活動,會提出問題的孩子比會回答問題的孩子具有更強的思考力.
(3)突破重難點的方法訓練.很多人的數學學習方法簡單四個字“題海戰術”.理科學習刷題是必要的,但是盲目地一份接一份地寫試卷,并不能真正突破重難點,應該強調專題化的訓練.以小學和初中階段都會涉及的“行程問題”為例,針對不同類型的“行程問題”,要掌握的學習方法是根據題意畫好線段圖,找好題意中路程、速度和時間之間的數量關系.行程問題有追及問題和相遇問題,解題方法可以用代數解也可以用方程解,有直接找出數量關系的,也有間接(通過比例)才能找出數量關系的.每種類型的提煉都是學生領悟的過程,題目不用多,通過專題類型的訓練,在初一年學習《一元一次方程》這個章節時,通過歸納總結,可以很好地解決小學階段沒有徹底參透的知識.這樣的訓練過程才能讓學生真正地理解利用數量(等量)關系解決實際問題的方法,這樣的“刷題”模式才能真正地鍛煉學生的學習能力.
小學與初中數學學習的銜接問題一直倍受家長和教師的關注,但是問題仍然存在.需要教師和家長形成共育模式,從課堂教學出發,關注學生的習慣和數學興趣的培養, 激發其學好數學的意識,多鉆研新課程教育理論知識,用更加符合學生心理需求的教學策略,切實有效地提高小學階段到初中數學的過渡,提高學生的數學學習能力.

