基于聲-固-壓電耦合的縱振水聲換能器工藝研究

耿鵬飛,田杜養,劉小光,程彩霞,冀邦杰

(中船西安東儀科工集團有限公司,陜西 西安,710065)

0 引言

縱振換能器是一種常用的大功率發射器,能夠以較小的質量和體積獲得較大的聲能密度,從而廣泛應用于超聲和水聲技術中。換能器的制造是設計、加工、裝配與測試一體化耦合過程。由于水聲換能器實際生產包括機械零件精密加工、陶瓷環篩選測試、陶瓷環涂膠粘接、換能器預緊裝配以及匹配層灌注等復雜的工藝過程,故生產工藝環節對換能器的相關電聲性能有一定影響。

針對在壓電陶瓷、電極及前后蓋板之間涂膠粘接問題,張福學[1]指出應用環氧樹脂膠合可以更好地傳遞聲波;閻福旺[2]論述了粘接的化學固化過程,并指出在固化過程中要對換能器進行加熱加壓處理,從實際換能器制作過程出發提出了膠粘劑對換能器性能的影響,但未對膠粘劑對換能器性能的具體影響程度進行分析及討論;張慶輝等[3]對縱振換能器性能進行數值研究和仿真分析,分析過程未考慮膠粘劑對換能器相關性能的影響;莫喜平[4]指出對高頻換能器的分析一般不可以忽略膠粘劑的影響,但在仿真中未給出相應考慮膠粘劑影響的換能器有限元模型,也未對具體影響程度進行分析。文中通過建立考慮膠粘劑的有限元模型,分析了膠粘劑涂抹對換能器在空氣中電聲性能的影響。

關于換能器壓電陶瓷環之間同軸度對縱振換能器性能影響的文獻較少,文中通過建立考慮壓電陶瓷環之間同軸度的有限元模型,分析了壓電陶瓷環同軸度對換能器諧振頻率及發送電壓響應的影響。

關于預應力對縱振換能器性能影響的文獻已有大量研究,榮德新[5]主要分析了縱振壓電換能器的預應力控制,張云電等[6]給出了基于計算機控制的壓電換能器恒扭矩裝配方法,但未能涉及預應力對換能器性能參數的影響;李軍等[7]基于實驗研究討論了壓電換能器共振頻率與預應力的關系,給出了施加預應力的參考值,但未能給出預應力對縱振換能器水下相關性能參數的影響。文中通過理論計算給出了該換能器預應力加載的適宜范圍,結合有限元仿真的方法,系統地研究了預應力通過影響壓電陶瓷材料的壓電性能參數,最終影響縱振換能器在空氣和水中的相關性能,并結合實驗驗證了其準確性。

目前,水聲換能器的研究方法主要有: 等效網絡法、瑞利法、有限差分法和有限元法[8]。結合工程實際應用背景,針對換能器在生產過程中的工藝環節,建立了三維有限元模型,分析了裝配過程中的相關因素對換能器的頻率響應和發射電壓響應的影響,系統研究了換能器裝配工藝中涂膠、陶瓷環裝配和預緊力施加過程,并制作了樣機,進行了聲學性能測試工作,獲得了詳細的聲學數據。將仿真數據與測試數據進行了對比,詳細分析了測試值與仿真值存在差異的主要原因。

1 基本理論

換能器本身存在集多物理場耦合在一起的復雜問題[9]。包括壓-電耦合分析、聲-固耦合分析和聲-固-壓電耦合分析。

系統的動力學方程為

式中:m為模態質量;c為模態剛度;d為模態阻尼;C為電容;R為電阻;α為機電轉換因子;U為輸入電壓;Q為輸入電荷;u為模態位移;FV為預緊力負載。

聲-固耦合在水域和換能器前輻射頭界面處的邊界上起作用,在邊界上建立雙向耦合。將前幅射頭的振動加速度用作聲源,在流體域中進行傳播。由壓力聲學計算得到的流體壓力作為反作用力施加在前輻射頭上。

聲壓分布的波動方程為

式中: ρ為密度;k為常數;P為聲壓。

仿真使用穩態研究步驟求解靜態應力分布。將該步驟得出的解作為線性化點,用于求解頻域擾動研究步驟中的振動問題。

1.1 涂膠粘接

換能器在實際裝配過程中,前蓋板、壓電陶瓷環、電極引片和后質量塊端面均用毛刷涂抹環氧樹脂后依次粘接,粘接完成后施加預緊力,隨后用綢布將換能器外側周圍擠壓出的殘膠擦拭干凈。經測量,膠層固化后零部件接觸表面粘接層厚度為0～0.02 mm。為了保證更好的粘接性能,在電極引片上設計多個均布的通孔,通孔處膠層厚度為0.15 mm。壓電陶瓷環內側依然存在殘膠,殘膠厚度為0.2～0.5 mm。

建立考慮粘接層、殘膠層及電極引片的壓電換能器模型,用于分析涂膠粘接對換能器相關電聲性能的影響。帶粘接層的1/6 換能器局部模型結構如下: 粘接層—電極引片—粘接層—壓電陶瓷層—粘接層—電極引片—粘接層,殘膠層位于壓電陶瓷環內側,如圖1 所示。

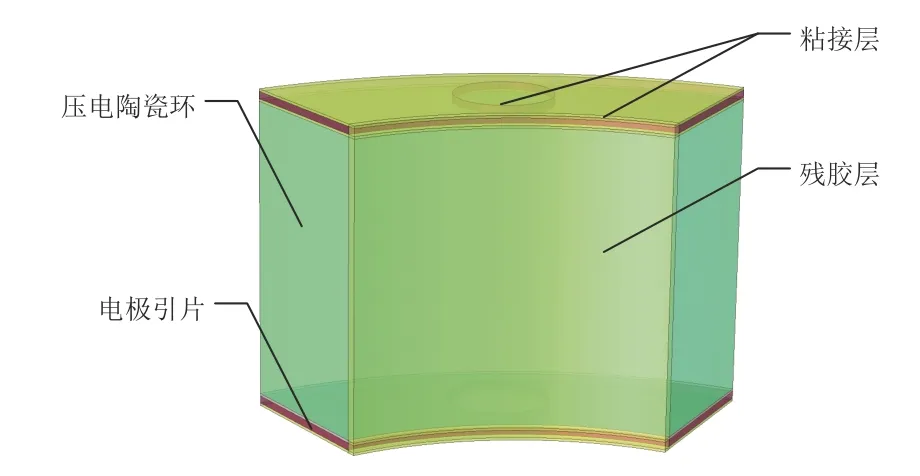
圖1 帶粘接層的1/6 換能器局部模型示意圖Fig.1 1/6 transducer model with an adhesive layer

1.2 結構件之間同軸度

換能器在裝配過程中,壓電陶瓷、電極引片、前蓋板和后質量塊通過預緊力螺栓串聯在一起,由于裝配過程為操作人員手工操作,故裝配完成后很難保證所有零件在同一軸線上,導致實際裝配模型和理論計算模型存在差異,故換能器相關性能也與理論值發生偏差。文中通過調整陶瓷環裝配,同軸度模擬實際裝配過程中陶瓷環裝配存在同軸度誤差的現象,分析裝配同軸度對換能器電聲性能的影響。

1.3 螺栓預緊力

依據縱振換能器的結構,換能器在給定聲功率發射時,節面所受的最大應力遠小于所施加的預緊力,故只結合預緊力對螺栓強度和壓電陶瓷性能的影響,給出該換能器預緊力加載的合適范圍。

考慮預緊力對螺栓的強度影響,文中使用的預應力螺栓采用2Cr13 馬氏體不銹鋼材料先淬火后回火。由于換能器結構會受到動載荷的影響,所以螺栓預緊力應適當調低,選擇在其屈服載荷的35%左右最為合適,最多不能超過70%。

螺栓預緊力為

式中:K1為預緊力系數,一般情況下為0.35～0.7;σS為 螺栓材料的屈服點;A1為螺栓應力橫截面積。

考慮預緊力對壓電陶瓷性能的影響,預緊力太小會導致各零件間接觸剛度下降,損耗增加,機電轉換效率下降,預緊力太大會導致壓電材料退極化。文中使用的材料本構模型基于實驗結果。該模型采用方法類似于文獻[10]描述方法,其中材料的壓電常數取決于壓電材料上的標稱FV,其值在 50 MPa 的預緊力下歸一化。材料的壓電屬性隨壓電材料預緊力的變化如圖2所示。

圖2 壓電常數隨預緊力變化Fig.2 Variation of piezoelectric constants with pretensioning force

陶瓷環預緊力為

式中: σt為壓電陶瓷環受到預緊力時內部預應力,一般情況為30～70 MPa;A2為壓電陶瓷環橫截面積。

螺栓擰緊力矩為

式中:K2為螺栓擰緊力矩系數,根據機械設計手冊選取該系數為0.15;d為螺紋公稱直徑。

經計算F1=6.3～12.6 kN,F2=5.1～11.9 kN,故選取FV=6.3～11.9 kN,M=5.7～10.7 N·m。

2 模型簡介及有限元建模

2.1 基本模型

換能器基本模型如圖3 所示,主要包括前蓋板、陶瓷環、質量塊、匹配層以及預緊力螺栓等。

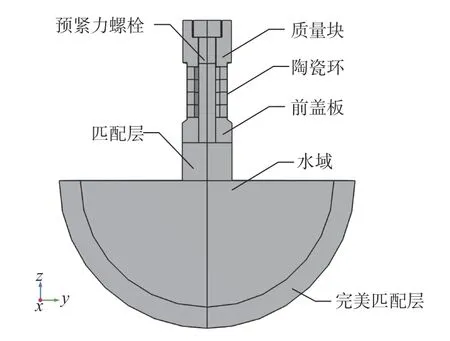
圖3 換能器三維模型Fig.3 3D model of transducer

為了計算無限水域的聲學特性,采用完美匹配層(perfect matched layer,PML)來構建一個封閉空間域,當散射波到達PML 時會被迅速吸收,形成一個無反射邊界,從而不會影響空間內的散射聲場[11]。

2.2 材料模型

帶匹配層縱振換能器前幅射頭采用2A12,材料密度2 780 kg?m-3,彈性模量為70.3 GPa,泊松比為0.345。后質量塊和預應力螺栓采用2Cr13,材料密度7 850 kg?m-3,彈性模量為210 GPa,泊松比為0.3。電極引片采用H62,材料密度8 960 kg?m-3,彈性模量為110 GPa,泊松比為0.35。匹配層采用環氧樹脂基復合材料,材料密度1 500 kg?m-3,彈性模量為7.6 GPa,泊松比為0.46。壓電陶瓷環采用PZT-4 材料,材料密度為7 500 kg?m-3,材料彈性常數、壓電應力常數和相對介電常數見表1[12-13];粘接層材料密度為1 700 kg?m-3,彈性模量為10 GPa,泊松比為0.38。

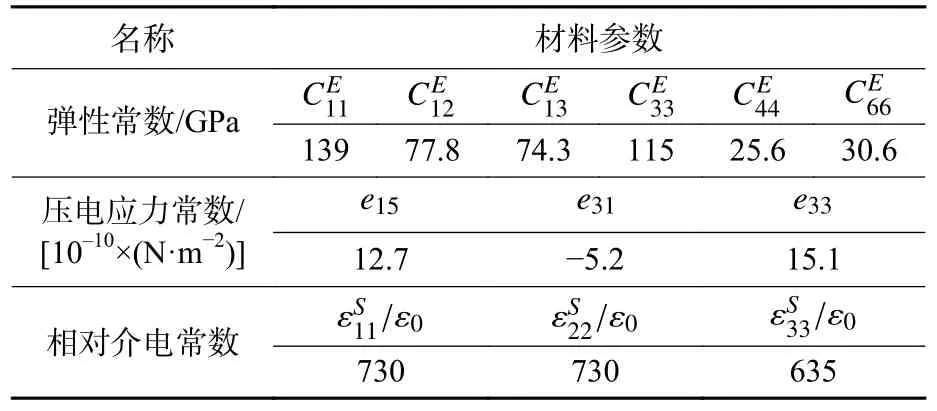
表1 PZT-4 材料參數Table 1 PZT-4 material parameters

2.3 網格劃分及邊界條件設定

為了精確解析水域中的聲壓波,需要將水域中最大網格單元大小定為最小波長的 1/5,則有

式中:V水=1 500 m/s 為水中聲速;fmax=50 kHz為換能器最大掃描頻率。

為了使網格平滑過渡,對固體域采用四面體網格劃分,最大網格尺寸為Lmax。對PML 創建5 層結構化網格。在鄰近外場邊界的內水域內創建邊界層網格,該層的厚度設為Lmax的 1/4,該邊層在內部自由四面體網格與外部結構化棱柱網格單元之間產生平滑過渡,從而使外場計算的精度更高。該網格模型共計5.8 萬網格單元,16.4 萬求解自由度。該有限元網格模型如圖4 所示。

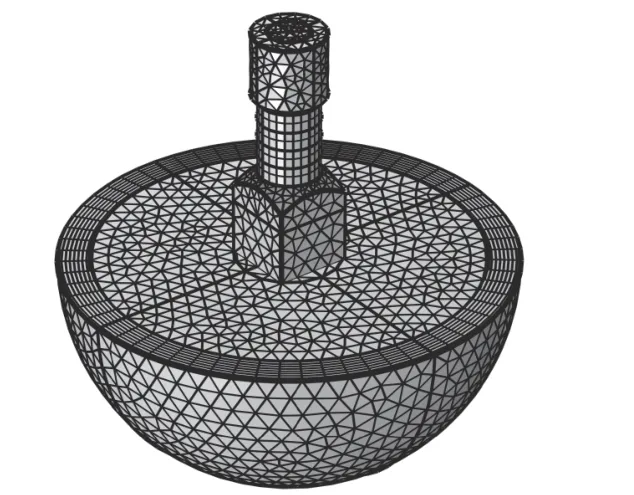
圖4 網格模型Fig.4 Mesh model

電壓邊界: 在對應的壓電陶瓷電極面施加電壓邊界條件,箭頭表示極化方向,其中2 個壓電陶瓷環沿+Z 向極化，另外2 個沿-Z 向極化，正負極之間電壓為1 V,如圖5所示。

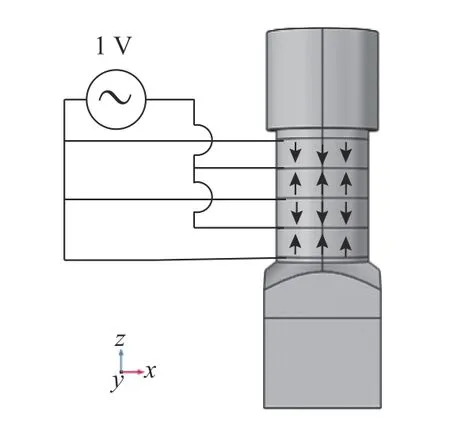
圖5 壓電陶瓷環極化方向和電連接示意圖Fig.5 Polarization direction and electrical connection of piezoelectric ceramic ring

預緊力邊界: 螺栓安裝在裝置上用于固定各個部件,螺栓擰緊過程會產生一個反作用力,表現為螺栓上的預緊力。由此產生的預應力有助于在裝置的正常工作期間將螺栓保持在固定位置。根據實際裝配過程建立接觸對并對預緊力截面施加擰緊力矩。

阻尼邊界: 在15～50 kHz內施加瑞利阻尼,定義阻尼系數為0.005。

位移邊界: 由于換能器在整個工作過程為自由狀態,故設定換能器空間自由度為6。

3 數值計算結果分析

3.1 涂膠粘接對換能器性能的影響

對換能器進行頻域分析,得到分別考慮粘接層、殘膠層的換能器模型在空氣中的電導隨頻率變化的有限元仿真對比曲線,如圖6 和圖7 所示,可以看出無粘接層和無殘膠層的理想換能器模型匹配前諧振頻率為26.85 kHz,帶粘接層的換能器模型匹配前諧振頻率為26.55 kHz,帶殘膠層的換能器模型匹配前諧振頻率為26.92 kHz,而3 種換能器模型諧振頻率處的電導值變化較小。

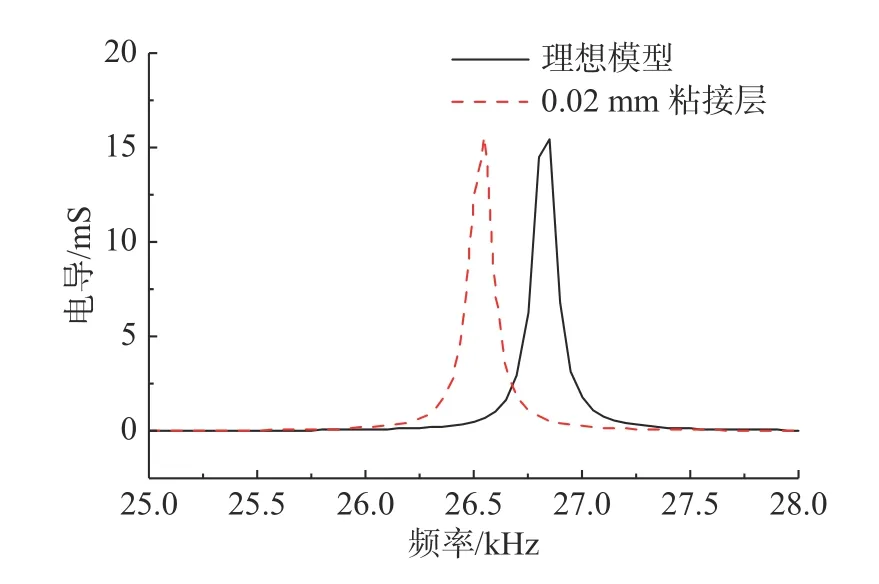
圖6 空氣中粘接層對換能器電導影響仿真曲線Fig.6 Simulation curves of the effect of adhesive layer on conductivity of transducer in air

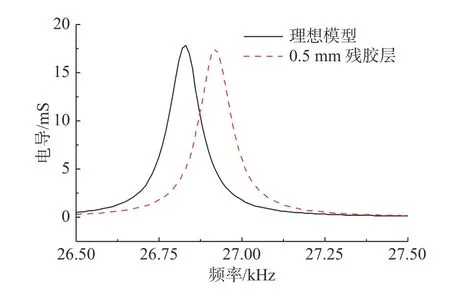
圖7 空氣中殘膠層對換能器電導影響仿真曲線Fig.7 Simulation curves of the effect of residual glue layer on conductivity of transducer in air

3.2 裝配同軸度對換能器性能的影響

對換能器進行頻域分析,得到2 種軸度下電導隨頻率變化的有限元仿真對比曲線,如圖8 所示。

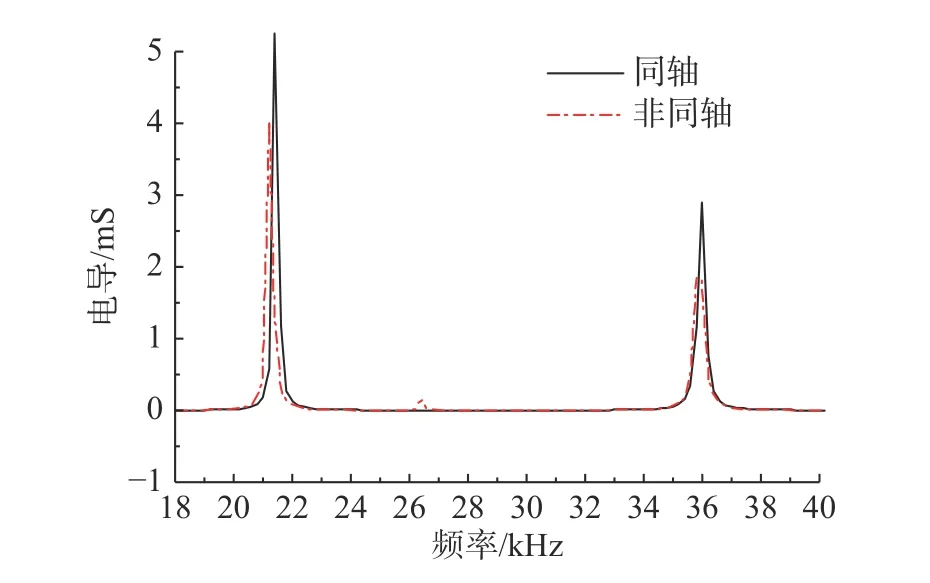
圖8 空氣中同軸和非同軸換能器電導隨頻率變化仿真曲線Fig.8 Simulation curves of conductivity with frequency of coaxial and non-coaxial transducers in air

圖8 和表2 中,同軸模型的換能器電導值比非同軸模型的換能器電導值高20%,且曲線光滑無毛刺。同軸度對換能器的固有頻率值影響可以忽略。

表2 空氣中同軸和非同軸換能器性能參數Table 2 Performance parameters of coaxial and noncoaxial transducers in air

圖9 給出了同軸模型和非同軸模型匹配層換能器在水中發送電壓響應(transmitting voltage response,TVR)曲線。可以看出,非同軸模型相比同軸模型TVR 降低約0.4～0.8 dB,此外,由于同軸度誤差的存在,換能器的1 階諧振頻率和2 階諧振頻率之間出現了2 處明顯的毛刺。

圖9 水中同軸和非同軸換能器TVR 隨頻率變化仿真曲線Fig.9 Simulation curves of TVR with frequency of coaxial and non-coaxial underwater transducers

3.3 預緊力對換能器性能的影響

建立預緊力模型,模擬實際裝配過程中施加預緊力的過程,分析預緊力對換能器性能的影響。

圖10 為帶匹配層換能器分別施加5.7、10.7 N·m的預緊力后其中的靜應力分布圖。可以看出,螺栓桿中的應力分布均勻,最大應力主要出現在螺栓桿以及螺栓正下方的后質量塊中心部分。

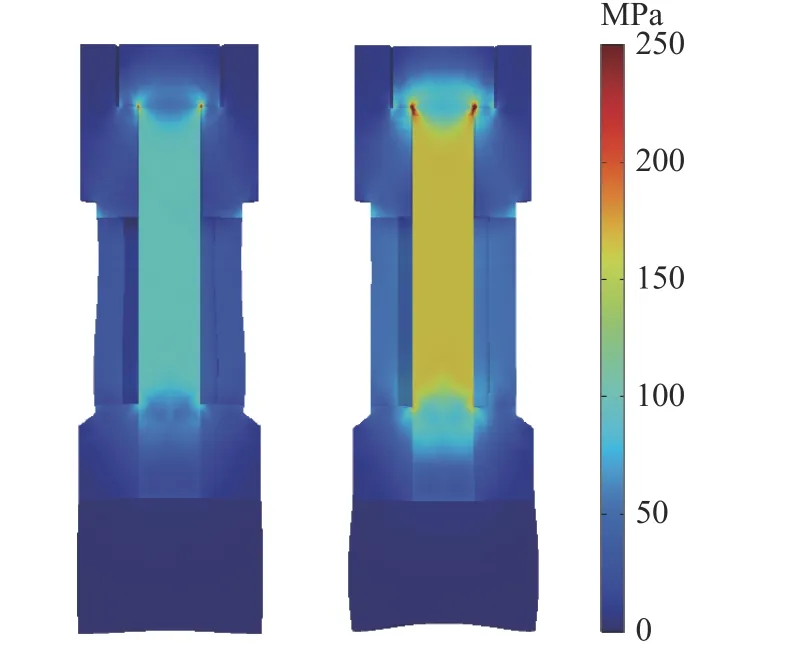
圖10 2 種預緊力下換能器中應力分布Fig.10 Stress distribution in transducers under two pretensioning forces

圖11、圖12 和表3 給出了施加2 種預緊力后換能器在匹配前后空氣中的電導隨頻率的變化情況。換能器諧振頻率和諧振頻率處的電導隨著預緊力增大而增大。換能器匹配前預緊力從5.7 N·m增大到10.7 N·m,諧振頻率增加1 kHz,諧振頻率處電導增大8%,匹配后1 階諧振頻率增加0.6 kHz,電導增大51%;2 階諧振頻率增加0.2 kHz,電導增大13%。

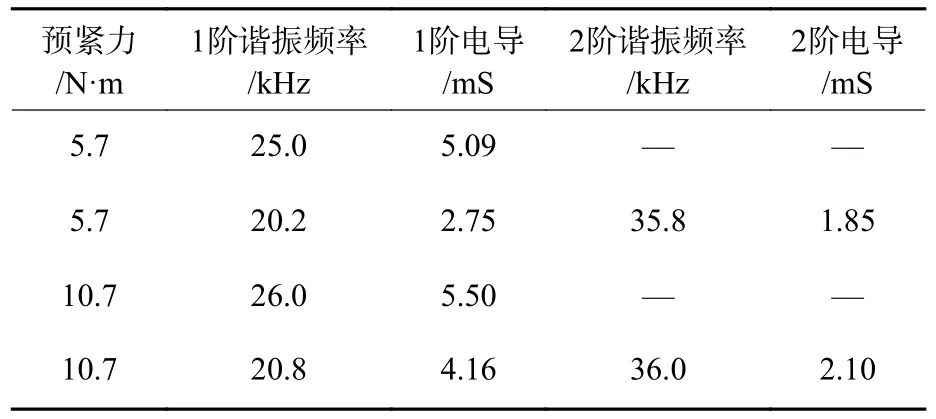
表3 空氣中2 種預緊力下換能器性能參數列表Table 3 Performance parameters of transducer under two pre-tensioning forces in air

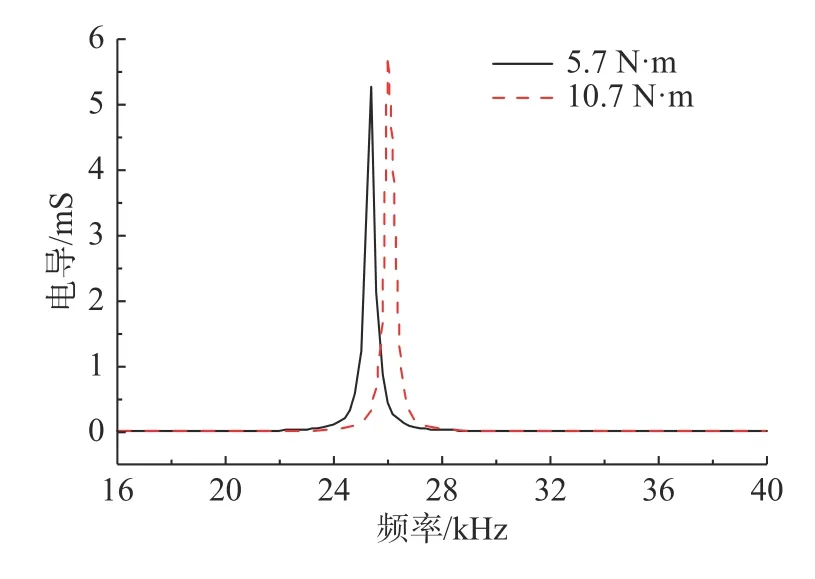
圖11 空氣中2 種預緊力下換能器電導隨頻率變化仿真曲線Fig.11 Simulation curves of conductivity with frequency of transducer under two pre-tensioning forces in air

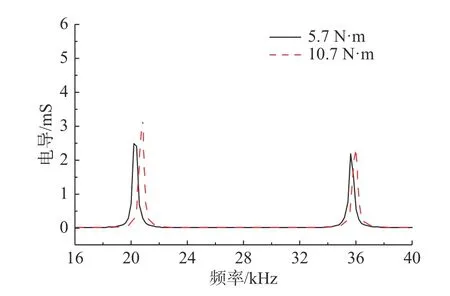
圖12 空氣中2 種預緊力下匹配層換能器電導隨頻率變化仿真曲線Fig.12 Simulation curves of conductivity with frequency of transducer with a matching layer under two pre-tensioning forces in air

圖13 給出了水中2 種螺栓預緊力下,TVR 隨頻率的變化,由曲線變化可以看出,隨著施加預緊力的增大,2 階固有頻率均增大;1 階固有頻率處TVR 降低,2 階固有頻率處TVR 升高,TVR 曲 線更加平坦。換能器在施加10.7 N·m 預緊力后20～34 kHz 相對平坦的區域適用于傳感應用。

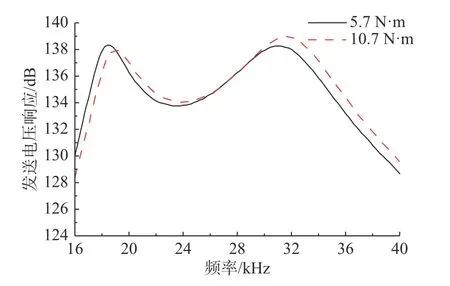
圖13 水中2 種預緊力下TVR 隨頻率變化曲線Fig.13 Simulation curves of TVR with frequency under two pre-tensioning forces in water

4 實測結果與分析

4.1 實驗測試方法

首先制作無膠裝配的換能器實物。經過靜置及高溫去除應力后進行測試,隨后將換能器拆解并進行涂膠裝配,通過裝配后換能器的高度保證粘接層厚度,再經過靜置及高溫去除應力后進行測試,以驗證粘接層對換能器電聲性能影響;采用膠槍噴涂(無殘膠)和毛刷涂抹2 種涂膠方式制作了不同的換能器,通過裝配后的質量估算陶瓷環內部殘膠層的厚度,經固化及去應力后進行測試,以驗證殘膠層對換能器電聲性能的影響;通過設計專用的換能器裝配工裝保證陶瓷環的同軸度,用以對比工裝裝配和手工裝配時不同同軸度對換能器電聲性能的影響;通過力矩扳手對換能器施加不同的預緊力,制作2 種預緊力下換能器實物,以驗證預緊力對換能器電聲性能的影響;最后將換能器前輻射面硫化后進行水池測試。試驗制作部分換能器實物如圖14 所示。

圖14 壓電換能器實物Fig.14 Physical piezoelectric transducer

4.2 實測分析

用4294A 阻抗分析儀在空氣介質中對匹配層灌注前后換能器的電導進行了測試,將制作好的換能器進行硫化,保證其密封性,然后在消聲水池進行聲性能測試,其結果如圖15～圖19 所示。

圖15 粘接層對換能器電導影響的仿真與實驗對比Fig.15 Comparison of simulation and experimental data on effect of adhesive layer on conductivity of transducer

圖15 可以看出,實際制作出的換能器無論是否涂抹粘接劑,其諧振頻率及電導值均小于仿真值;仿真計算中,在換能器模型加入粘接層后,其諧振頻率降低了約0.3 kHz;而實際測試中,加入粘接層后,其諧振頻率升高了約0.4 kHz。無論是仿真計算還是實際測試,粘接層對諧振頻率和電導值的影響都比較小。

圖16 可以看出,殘膠層使換能器的諧振頻率升高,但對電導值影響較小。

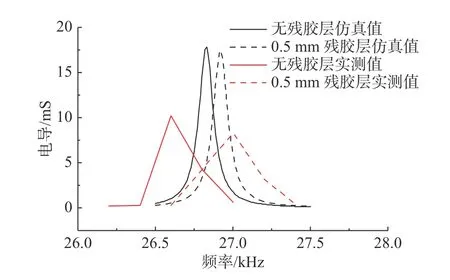
圖16 殘膠層對換能器電導影響的仿真與實驗對比Fig.16 Comparison of simulation and experimental data on effect of residual glue layer on conductivity of transducers

圖15 和圖16 中粘接層和殘膠層均通過影響陶瓷環來影響換能器的電聲性能。陶瓷環的諧振頻率方程為

式中:f為諧振頻率;E為彈性模量;r2為陶瓷環外徑;r1為陶瓷環內徑;d33為軸向壓電常數;h為厚度。

粘接層通過填補各零件端面間的微小空隙來影響壓電陶瓷環的整體剛性,使綜合彈性模量提高壓電陶瓷環的整體剛性,進而增大綜合彈性模量,導致諧振頻率f增大,另一方面粘接層使得陶瓷環裝配體整體厚度h增大,諧振頻率降低;殘膠層使得陶瓷環裝配體整體內徑r1增大,導致諧振頻率f增大。

圖17 中,非同軸裝配的換能器TVR 曲線在27 kHz 處出現明顯毛刺;圖18 和圖19 中,隨著預緊力從5.7 N·m 增大到10.7 N·m,諧振頻率增大約1.2 kHz,在諧振頻率處的電導值也隨之增大,換能器TVR 曲線明顯后移。整體而言,仿真值與實測結果具有較好的一致性。由于真實材料內部不均勻,真實性能參數和仿真材料參數存在差異;有限元模型將換能器各個零件接觸關系定義為理想面接觸,而實際上各個零件之間微觀上為局部點接觸;實際測試中由于存在測量誤差,測試值與真實值也存在差異。

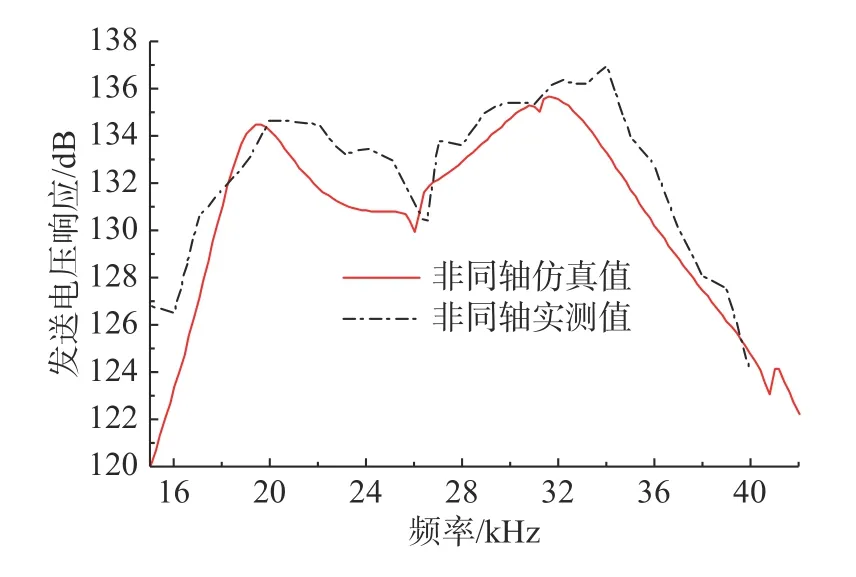
圖17 非同軸裝配方式下換能器TVR 仿真與實驗對比Fig.17 Comparison of simulation and experimental data of TVR for non-coaxial assembly mode of transducer

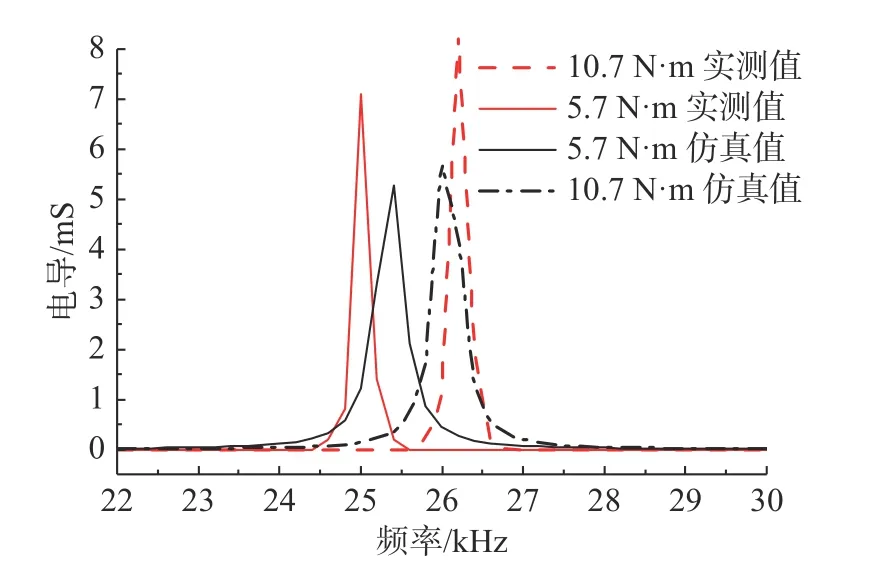
圖18 2 種螺栓預緊力下電導隨頻率變化的仿真與實驗數據對比Fig.18 Comparison of simulation and experimental data of conductivity variation with frequency under two bolt pre-tensioning force levels

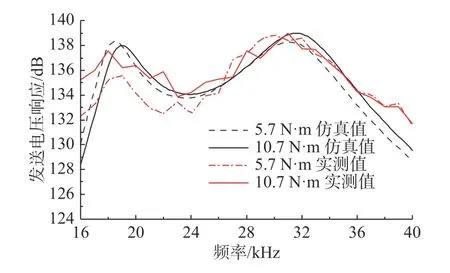
圖19 2 種螺栓預緊力下TVR 仿真與實驗對比Fig.19 Comparison of simulation and experimental data of TVR under two bolt pre-tensioning force levels

5 結論

采用有限元分析和試驗驗證的方法從2 個層面對匹配層換能器進行了較為深入的研究,通過研究可知:

1) 換能器涂膠粘接可以通過填補各零件端面間的微小空隙來提高壓電陶瓷環的整體剛性,進而使得綜合彈性模量增大,從而導致諧振頻率增加;

2) 換能器諧振頻率隨著粘接層厚度增大而減小,隨著殘膠層厚度增大而增大;

3) 陶瓷環裝配同軸度高的換能器TVR 曲線毛刺較少,曲線更加平坦,更適合傳感應用;

4) 隨著預緊力增大,換能器的1、2 階諧振頻率增幅較明顯,發送電壓響應曲線明顯后移,生產過程中可以通過施加合適的預緊力使換能器調節至預期的工作頻帶內。

研究結果對換能器工藝研究具有指導意義,可有效提高換能器裝配的合格率。