基于自抗擾控制的車用異步電機參數辨識

張世龍，李軍偉，李連強，王東

(1.山東理工大學 交通與車輛工程學院，山東 淄博 255049；2.一汽解放青島汽車有限公司，山東 青島 266200；3. 北京乾勤科技發展有限公司，北京 100084)

隨著變頻調速技術的發展,交流異步電機控制技術也更加成熟,控制更加方便,控制精度越來越高,因此交流異步電機的應用場合也愈加廣闊。通常采用基于磁場定向的矢量控制方法實現對交流異步電機的高性能控制,這種控制方法需要較為準確的電機參數,如轉子時間常數等[1]。由于轉子時間常數對磁鏈和轉矩的解耦具有較大影響,因此,需要一種能夠在線辨識轉子時間常數的辨識方案,確保交流異步電機在不同工況下的控制性能。

電機參數辨識有多種方法,包含模型參考自適應算法、最小二乘法及擴展卡爾曼濾波法等[2]。吳錦宇[3]利用模型參考自適應算法,使用基于無功功率模型對轉子時間常數進行辨識,得到了準確的辨識結果。王曉晨[4]利用ICS算法和MRAS相結合的方法對電機的交直軸電感進行辨識,得到了準確的交直軸電感。

為避免轉子時間常數變化對基于轉子磁場的矢量控制系統的影響,本文以定子側的電壓、電流信號以及轉子速度作為輸入量,采用基于MRAS和GA-ADRC結合的方法,實現對轉子時間常數的在線辨識并通過仿真實驗驗證該方法的可行性。

1 轉子時間常數辨識公式推導

本文使用模型參考自適應算法對轉子時間常數進行辨識,利用基于轉子磁鏈的電流模型設計模型參考自適應算法的可調模型,如式(1)所示。根據轉子磁鏈的電壓模型設計模型參考自適應算法的參考模型,如式(2)所示。

(1)

(2)

根據Popov超穩定原理設計自適應機構,如式(3)所示。

(3)

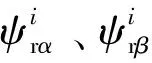
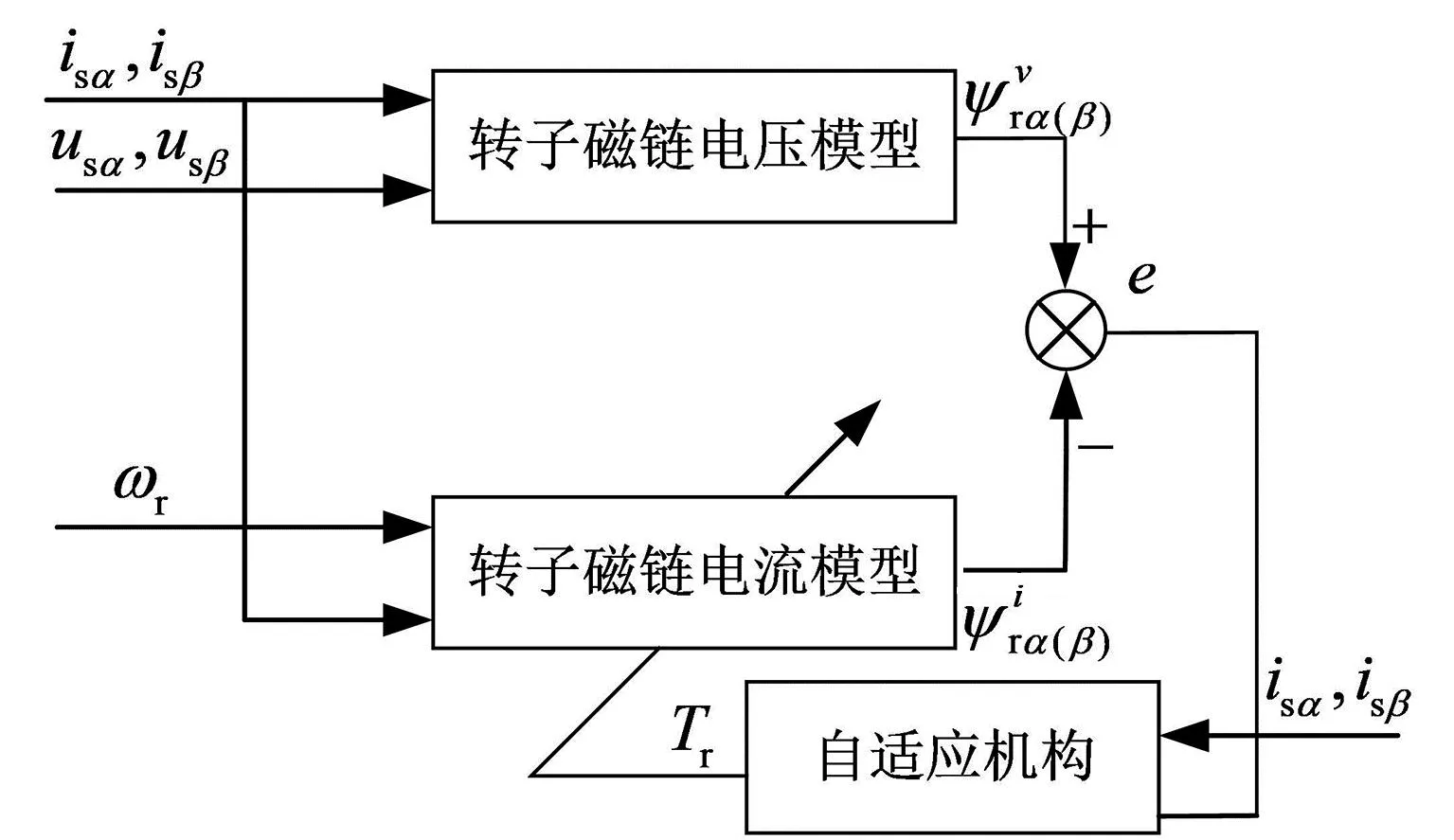
圖1 轉子時間常數辨識框圖

基于轉子磁鏈的電壓模型含有純積分,會出現積分飽和問題[5],導致出現直流偏置的現象,使得轉子時間常數辨識不準確。同時,定子電阻隨電機溫度的變化而變化,導致基于轉子磁鏈的電壓模型輸出的轉子磁鏈不準確[6],無法作為參考模型的輸出。因此,需要對辨識模型進行優化。

2 基于MRAS的轉子時間常數辨識模型優化

本文提出基于MRAS和GA-ADRC相結合的方法對轉子時間常數進行辨識,并將其應用在交流異步電機矢量控制系統中,其整體框架如圖2所示。

圖2中,在交流異步電機矢量控制系統的基礎上添加參數辨識模型,辨識模型輸出的轉子時間常數會反饋到磁鏈觀測器,實現了勵磁與轉矩的解耦[7]。

基于MRAS和GA-ADRC的轉子時間常數辨識框圖如圖3所示。圖3中,通過轉子磁鏈的電壓和電流模型對轉子時間常數進行辨識,通過定子磁鏈的電壓和電流模型對定子電阻進行辨識[8]。將定子電阻辨識值反饋至轉子磁鏈的電流模型,以消除定子電阻對參考模型的影響。為提高轉子時間常數辨識結果的準確性,本文基于GA-ADRC對自適應機構的調節參數進行優化。

圖2 基于MRAS和GA-ADRC參數辨識的交流異步電機矢量控制框圖

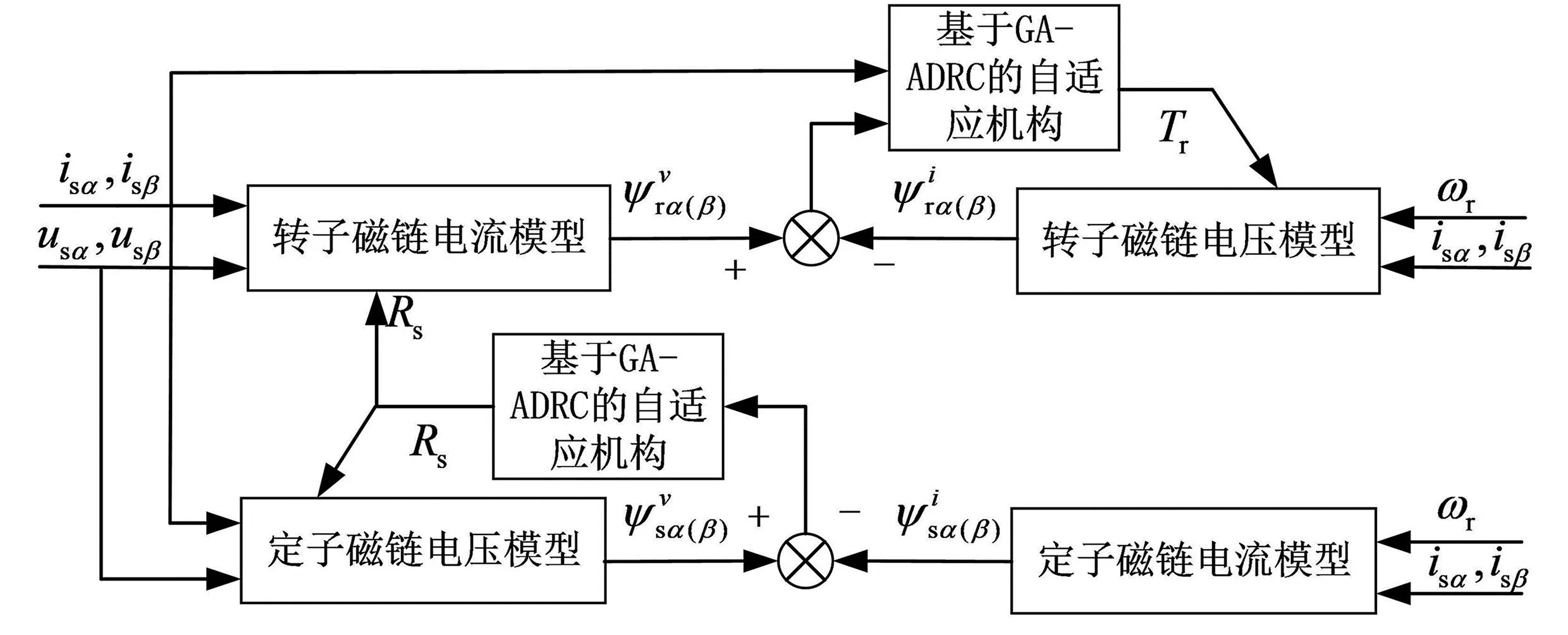
圖3 基于MRAS和GA-ADRC的轉子時間常數辨識框圖

2.1 基于MRAS的轉子時間常數優化辨識

由式(2)可知,基于轉子磁鏈的電壓模型含有純積分,會出現積分飽和問題,導致辨識效果不理想,本文將電壓模型與低通濾波器相結合,以消除積分飽和對轉子磁鏈電壓模型的影響,優化后的轉子時間常數辨識數學模型如式(4)和式(5)所示。

(4)

(5)

式(5)中ωcl為截止頻率。為消除低通濾波器引起的相位偏差,對截止頻率進行實時調整。當轉子角速度低于或等于200 rad/s時,截止頻率設置為30 rad/s;當轉子角速度高于200 rad/s時,截止頻率設置為0.15倍的轉子角速度。

為避免定子電阻變化對轉子時間常數辨識造成影響,本文對定子電阻進行辨識,并將定子電阻辨識值作為參考模型的輸入量,傳給轉子時間常數辨識模型,以提高轉子時間常數辨識的準確性。

本文使用定子磁鏈的電壓模型對模型參考自適應算法的可調模型進行設計,如式(6)所示。使用定子磁鏈的電流模型對模型參考自適應算法的參考模型進行設計,如式(7)所示。

(6)

(7)

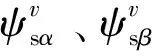
根據Popov超穩定性原理設計自適應機構如式(8)所示。

(8)

式中kp1、ki1分別為定子電阻辨識的增益參數。

2.2 GA-ADRC控制器設計

基于GA-ADRC的自適應機構框圖如圖4所示。遺傳算法基本思想是通過對運行參數初始化,獲得第一代種群個體,然后通過選擇、交叉以及變異操作,求取個體適應度值,根據適應度值對個體進行評價,得到優秀的個體[9]。遺傳算法的核心是適應度函數的選取和設計。本文選取的適應度函數由超調量、調整時間和轉子磁鏈誤差三部分組成,如式(9)所示。

f=0.1ts+0.8δ+0.1Mp

(9)

式中：ts為調整時間,δ為轉子磁鏈誤差,Mp為超調量。

自抗擾控制包含跟蹤微分器、擴張狀態觀測器和線性狀態誤差反饋控制率三部分[10]。跟蹤微分器和線性狀態誤差反饋控制率可以控制被控量快速達到穩定值且無超調。擴張狀態觀測器可以將被控量建模所涉及的動態未知部分和外部帶來的擾動干擾歸納為對整體的總干擾,并對其進行估計和補償。

本文以轉子磁鏈控制為目標對ADRC控制器進行設計。轉子磁鏈在d_q坐標系下的數學模型如式(10)所示。

(10)

式中：ψr為轉子磁鏈,isd為勵磁電流,ω1為同步旋轉電角速度。

1)跟蹤微分器。跟蹤微分器以轉子磁鏈作為輸入信號,輸出信號為θ(k)和ψr(k), 其中θ(k)為跟蹤輸入信號,ψr(k)為θ(k)的微分。

對電機控制系統進行離散化處理得

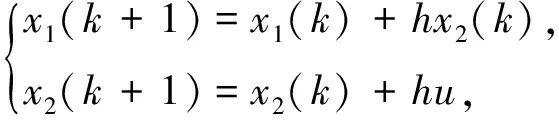
(11)

式中u=fst(x1,x2,r,h)為快速控制最優綜合函數。將u=fst(x1,x2,r,h)代入式(11),化簡得快速離散跟蹤微分器如式(12)所示。

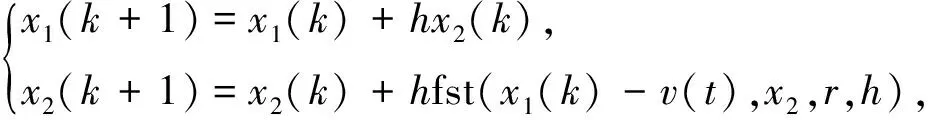
(12)

式中：h為設定采樣周期,v(t)為輸入信號。

將轉子磁鏈代入式(12)并化簡可得跟蹤微分器方程

(13)

式中e0為轉子磁鏈的偏差。

2)擴張狀態觀測器。d_q坐標系中,轉子磁鏈數學模型中的 “擾動部分”包含互感與轉矩電流的耦合項,以及一些受工況變化的定轉子電阻等電機參數,將其歸納為擾動項,利用擴張狀態觀測器進行估計和補償。

對于電機非線性控制系統,可得如下觀測器公式：

(14)

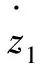
(15)

由式(13)—式(15)可得電機控制系統的擴張狀態觀測器方程為

(16)

式中：u(k)表示輸入量,β1、β2以及β3為ESO的控制參數,ψr(k)為電機轉子磁鏈,b為增益系數。

3)線性誤差反饋控制率。誤差反饋系統包含線性和非線性兩種反饋控制策略,本文采用線性反饋控制策略,誤差反饋率方程為

u(k)=α1(θ(k)-z1(k))+α2(ω(k)-z2(k)),

(17)

式中α1和α2為控制參數,該參數用來調節系統輸出。

通過遺傳算法整定ADRC參數步驟如下：

1)對運行參數進行初始化設置,包括進化迭代次數、種群規模、交叉概率、變異概率以及節點信息。選取ADRC控制中的β1、β2以及β3作為遺傳算法中的種群個體。

2)通過初始化種群獲得第一代個體,然后將需要整定的ADRC控制器參數賦值,運行交流異步電機參數辨識控制系統。

3)在主循環中運行選擇、交叉和變異操作,計算種群和個體的適應度,對種群進行優勝劣汰,然后更新種群和個體的適應度值。交叉操作和變異操作的計算公式如式(18)、式(19)所示。

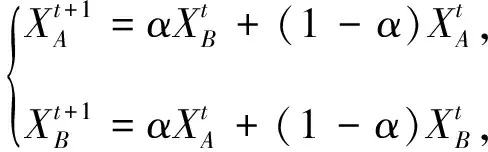
(18)

式中：α為一定范圍內的隨機數,XA、XB為種群的兩個個體。

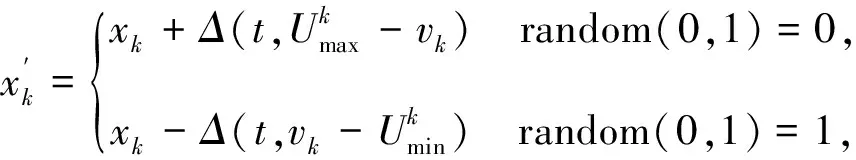
(19)

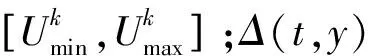
4)運行至設定的最大迭代次數為止,此時輸出的ADRC參數即為經過遺傳算法整定后的優化參數。

遺傳算法優化ADRC參數流程如圖5所示。圖5中,通過浮點數編碼對種群進行初始化設置,然后將種群個體賦值給電機矢量控制系統的自適應機構。通過sim函數調用交流異步電機控制系統,模型文件運行完畢后會得到轉子磁鏈的大小、調整時間以及超調量的值。利用適應度函數計算每一次迭代時的適應度值并進行記錄,由此得到個體極值和種群在全局下的極值。對上一代優化得到的優秀個體再次進行選擇、交叉和變異操作,將得到的新的個體值帶入到式(9)中計算種群個體適應度值,將此值與上一代最優值進行比較,根據適應度值將不合適的種群淘汰。在迭代次數內多次運行電機矢量控制系統,將每次得到的全局最優值進行比較,當達到最大迭代次數時,輸出最終的β1、β2和β3。

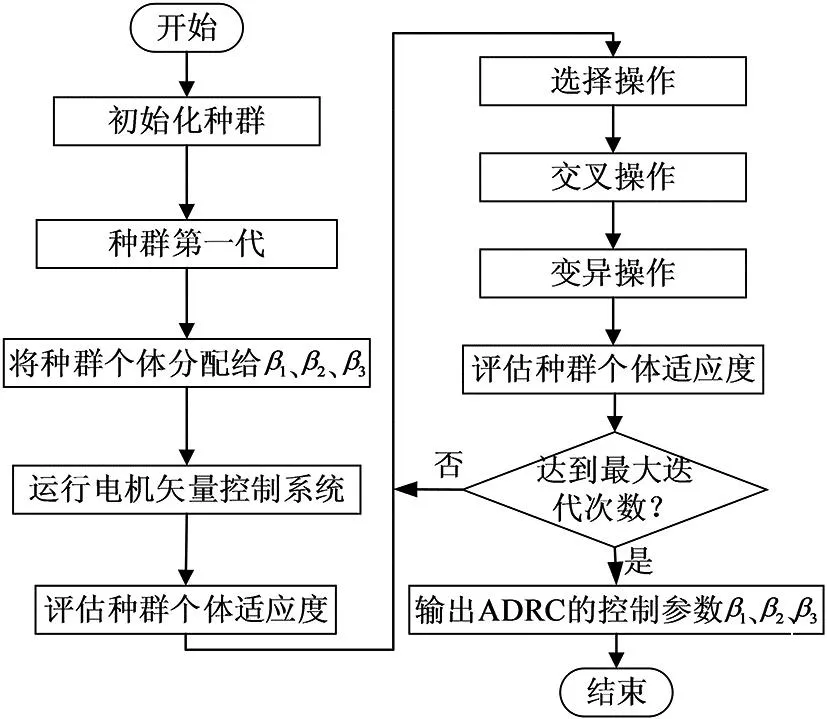
圖5 遺傳算法優化ADRC參數流程圖

3 仿真分析

利用MATLAB/Simulink搭建交流異步電機參數辨識矢量控制系統,利用仿真實驗驗證矢量控制系統和轉子時間常數辨識模型的有效性[11],相關實驗參數見表1。

表1 交流感應電機仿真性能參數

本文采用MRAS和GA-ADRC相結合的方法,對轉子時間常數進行在線辨識,通過對比試驗,觀察轉子時間常數辨識在電機控制系統中所起的作用。仿真工況設置如下：設定運行轉速1 000 r/min,分別改變轉子電阻和定子電阻,其中轉子電阻在0～<0.3 s時保持0.37 Ω不變,在0.3 s時由0.37 Ω變為0.16 Ω,同時給定10 N·m的負載,觀察轉子時間常數辨識值是否跟隨變化;定子電阻在0～<0.5 s時保持初始值0.5 Ω不變,在0.5 s時由0.5 Ω增大為0.9 Ω。仿真實驗結果如圖6—圖9所示。

圖6 轉子時間常數的響應曲線

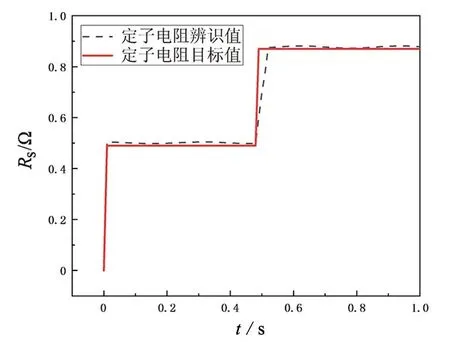
圖7 定子電阻的響應曲線

圖8 轉速響應的對比曲線

圖9 轉矩響應的對比曲線

圖6為轉子時間常數的響應曲線,由圖6可知,在0～<0.3 s內轉子電阻保持0.37 Ω不變,在0.3 s時轉子電阻由0.37 Ω變為0.16 Ω,轉子時間常數辨識值跟隨目標值,辨識無錯誤;在0.5 s時定子電阻由0.5 Ω增大為0.9 Ω,轉子磁鏈電壓模型中的定子電阻隨定子電阻辨識模型發生了改變,轉子時間常數辨識結果正常,證明該方法可以有效辨識轉子時間常數的變化。

圖7為定子電阻的響應曲線,由圖7可知,在0～<0.5 s內定子電阻保持0.5 Ω不變,在0.5 s時定子電阻由0.5 Ω增大為0.9 Ω,定子電阻辨識值跟隨目標值,證明該方法可以有效辨識定子電阻的變化。

圖8為轉子電阻在0.3 s時由0.37 Ω變為0.16 Ω和定子電阻在0.5 s時由0.5 Ω增大為0.9 Ω時,矢量控制系統和參數辨識系統的轉速響應。由圖8可知,參數辨識系統的轉速到達穩態時間相比于矢量控制系統提高了約10 ms,在0.3 s時,施加10 N·m的負載,辨識系統下的轉速約下降2 r/min,矢量控制系統下的轉速約下降4 r/min,辨識系統相比于矢量控制系統抗干擾性更好。在0.5 s時,定子電阻由0.5 Ω增大為0.9 Ω,矢量控制系統下的轉速由于勵磁和轉矩無法正常解耦,轉速開始緩慢降低,在0.62 s時轉速突然下降和震蕩,響應效果變差。兩者對比可知,辨識系統相比于矢量控制系統具有更好的控制性能。

圖9為轉子電阻在0.3 s時由0.37 Ω變為0.16 Ω和定子電阻在0.5 s時由0.5 Ω增大為0.9 Ω時,矢量控制系統和參數辨識系統的轉矩響應。由圖9可知,參數辨識系統的轉矩到達穩態的時間相比于矢量控制系統更快,達到穩定轉矩的時間縮短了約50 ms。在0.3 s時,施加10 N·m的負載,辨識系統相對于矢量控制系統的響應時間更快,縮短了約8 ms,辨識系統的轉矩波動更小,更接近參考值。由于轉動慣量和系統阻尼等因素的影響,導致辨識系統和矢量控制系統的轉矩比參考值增加了0.5 N·m。在0.5 s時,定子電阻由0.5 Ω增大為0.9 Ω,此時矢量控制系統中勵磁和轉矩無法正常解耦,導致轉矩突然震蕩,響應效果變差。

實驗結果表明,MRAS與GA-ADRC結合的方法可以有效辨識轉子時間常數,從而提高交流異步電機控制系統的控制效果。

4 結論

本文提出了一種MRAS與GA-ADRC相結合的參數辨識方法對轉子時間常數進行辨識,使用GA-ADRC對自適應機構中的參數進行優化,并對參數辨識控制系統進行了仿真驗證,得出以下結論：

1) 當轉子時間常數隨電機運行工況變化而改變時,若不能準確修正,會導致電機轉速劇烈震蕩且無法輸出正常轉矩。

2) 本文采用MRAS與GA-ADRC相結合的方法對轉子時間常數進行辨識,當定子電阻和轉子電阻發生變化時,可以準確辨識出轉子時間常數的變化,避免轉速和轉矩出現震蕩現象,縮短了轉矩達到穩態的響應時間。MRAS與GA-ADRC相結合的方法使交流異步電機控制系統具有良好的動態響應特性,提高了控制系統的抗干擾能力。