幺半群中最小的變色龍

DOI：10.16783/j.cnki.nwnuz.2024.01.001

收稿日期：20230624;修改稿收到日期：20230818

作者簡(jiǎn)介：李永康（1973—），男，中國(guó)香港人，教授，博士.主要研究方向?yàn)榘肴捍鷶?shù).

Email：edmond.lee@nova.edu

摘要：稱一個(gè)半群為變色龍，如果它既是一個(gè)有限基對(duì)合半群的約簡(jiǎn)，又是一個(gè)非有限基對(duì)合半群的約簡(jiǎn).目前已知的變色龍最小的階數(shù)為8，本文構(gòu)造了兩個(gè)階數(shù)更小的變色龍，一個(gè)是階數(shù)為7的半群，另一個(gè)是階數(shù)為6的幺半群，后者恰好是幺半群中階數(shù)最小的一個(gè)變色龍.

關(guān)鍵詞：半群；幺半群；對(duì)合半群；有限基；變色龍

中圖分類號(hào)：O 153.5??? 文獻(xiàn)標(biāo)志碼：A??? 文章編號(hào)：1001-988Ⅹ（2024）01-0001-04

A smallest chameleon among monoids

LEE Edmond W H

（Department of Mathematics，Nova Southeastern University，F(xiàn)lorida 33328，USA）

Abstract：A semigroup is a chameleon if it is the reduct of both a finitely based involution semigroup and a non-finitely based involution semigroup.Presently，the smallest published example of a chameleon is of order eight.This article constructs two smaller examples：a semigroup of order seven and a monoid of order six.The latter turns out to be a smallest chameleon among monoids.

Key words：semigroup;monoid;involution semigroup;finitely based;chameleon

稱一個(gè)代數(shù)為有限基的，如果它的等式可以有限公理化.許多重要代數(shù)類的有限成員都是有限基的，例如群［1］、結(jié)合環(huán)［2-3］和李代數(shù)［4］.但不是所有的有限代數(shù)都是有限基的.有限基問題，即確定哪些有限型的有限代數(shù)是有限基的，在一般情況下是不可判定的［5］.對(duì)于有限半群和有限對(duì)合半群，雖然近幾十年得到了廣泛研究，但它們的有限基問題仍未解決.稱S，*為對(duì)合半群，如果S為半群，且“*”為滿足以下等式的一元運(yùn)算：

（x*）*≈x， （xy）*≈y*x*.（1）

稱此一元運(yùn)算“*”為S的對(duì)合運(yùn)算.常見的例子是： 群G在逆映射“-1”下構(gòu)成的對(duì)合半群G，-1，矩陣半群Mn 在轉(zhuǎn)置“T”下構(gòu)成的對(duì)合半群Mn，T.

雖然半群和對(duì)合半群在許多方面相似，但它們的等式性質(zhì)可能會(huì)有很大的差異.尤其值得注意的是，對(duì)合半群S，*及其約簡(jiǎn)S不一定同時(shí)是有限基的［6-10］.在研究對(duì)合半群的等式時(shí)，另一個(gè)有趣的現(xiàn)象是：存在一個(gè)半群S既是一個(gè)有限基對(duì)合半群S，*的約簡(jiǎn)又是一個(gè)非有限基對(duì)合半群S，的約簡(jiǎn)［9-11］，為了方便起見，稱這樣的半群S為變色龍.

目前已知變色龍中階數(shù)最小的為8：它是由一個(gè)非有限基6階半群與一個(gè)3階循環(huán)群或3階非鏈半格合并而成的［10-12］.一個(gè)有趣的問題是：是否存在更小階數(shù)的變色龍.本文構(gòu)造了一個(gè)7階的變色龍和一個(gè)6階的變色龍，后者恰好是一個(gè)幺半群，并證明了6階變色龍是幺半群中階數(shù)最小的一個(gè).

在非幺半群的半群中，是否存在小于6階的變色龍？目前已經(jīng)知道不存在階數(shù)小于等于3的變色龍，這是因?yàn)槊總€(gè)階數(shù)小于等于3的對(duì)合半群都是有限基的［13］.

問題1? 是否存在4階或者5階的變色龍？

本文變色龍可以稱為等式化的，因?yàn)樵诓煌膶?duì)合運(yùn)算下，它們變成具有不同等式特性的對(duì)合半群.值得注意的是，可以定義其他類型的變色龍，例如存在具有兩個(gè)對(duì)合運(yùn)算“*”和“”的半群S，其中簇VarS，*包含有限多個(gè)子簇，但簇VarS，包含不可數(shù)多個(gè)子簇［14］.

更多關(guān)于對(duì)合半群簇的信息可見文獻(xiàn)［15-16］.

1? 7階變色龍

半群

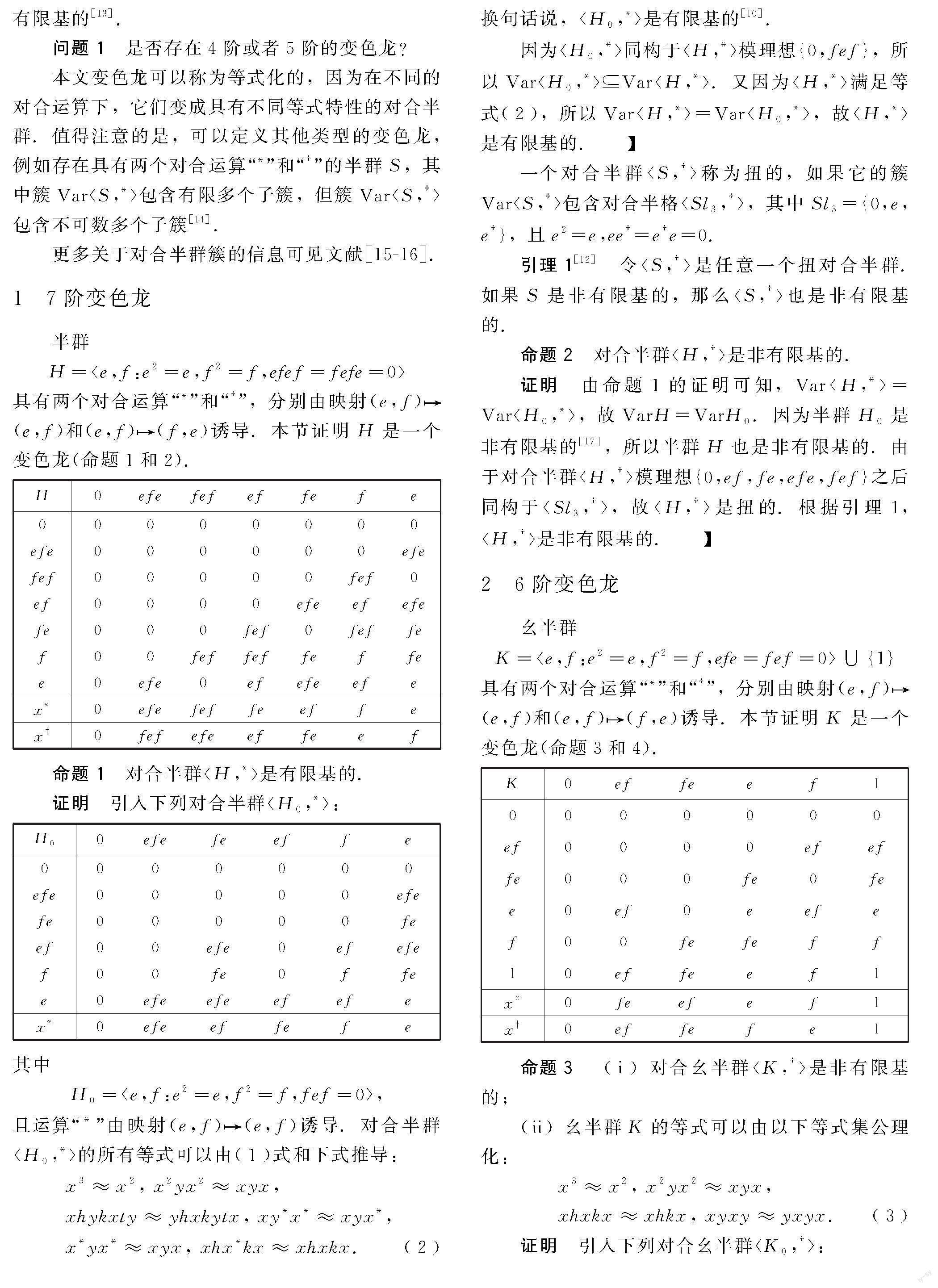
H=e，f：e2=e，f2=f，efef=fefe=0

具有兩個(gè)對(duì)合運(yùn)算“*”和“”，分別由映射（e，f）（e，f）和（e，f）（f，e）誘導(dǎo).本節(jié)證明H是一個(gè)變色龍（命題1和2）.

H0efefefeffefe

00000000

efe000000efe

fef00000fef0

ef0000efeefefe

fe000fef0feffe

f00feffeffeffe

e0efe0efefeefe

x*0efefeffeeffe

x0fefefeeffeef

命題1? 對(duì)合半群H，*是有限基的.

證明? 引入下列對(duì)合半群H0，*：

H00efefeeffe

0000000

efe00000efe

fe00000fe

ef00efe0efefe

f00fe0ffe

e0efeefeefefe

x*0efeeffefe

其中

H0=e，f：e2=e，f2=f，fef=0，

且運(yùn)算“*”由映射（e，f）（e，f）誘導(dǎo).對(duì)合半群H0，*的所有等式可以由（1）式和下式推導(dǎo)：

x3≈x2， x2yx2≈xyx，

xhykxty≈yhxkytx， xy*x*≈xyx*，

x*yx*≈xyx， xhx*kx≈xhxkx.（2）

換句話說，H0，*是有限基的［10］.

因?yàn)镠0，*同構(gòu)于H，*模理想{0，fef}，所以VarH0，*VarH，*.又因?yàn)镠，*滿足等式（2），所以VarH，*=VarH0，*，故H，*是有限基的.? 】

一個(gè)對(duì)合半群S，稱為扭的，如果它的簇VarS，包含對(duì)合半格Sl3，，其中Sl3={0，e，e}，且e2=e，ee=ee=0.

引理1［12］? 令S，是任意一個(gè)扭對(duì)合半群.如果S是非有限基的，那么S，也是非有限基的.

命題2? 對(duì)合半群H，是非有限基的.

證明? 由命題1的證明可知，VarH，*=VarH0，*，故VarH=VarH0.因?yàn)榘肴篐0是非有限基的［17］，所以半群H也是非有限基的.由于對(duì)合半群H，模理想{0，ef，fe，efe，fef}之后同構(gòu)于Sl3，，故H，是扭的.根據(jù)引理1，H，是非有限基的.? 】

2? 6階變色龍

幺半群

K=e，f：e2=e，f2=f，efe=fef=0∪{1}

具有兩個(gè)對(duì)合運(yùn)算“*”和“”，分別由映射（e，f）（e，f）和（e，f）（f，e）誘導(dǎo).本節(jié)證明K是一個(gè)變色龍（命題3和4）.

K0effeef1

0000000

ef0000efef

fe000fe0fe

e0ef0eefe

f00fefeff

10effeef1

x*0feefef1

x0effefe1

命題3? （i）對(duì)合幺半群K，是非有限基的;

（ii）幺半群K的等式可以由以下等式集公理化：

x3≈x2， x2yx2≈xyx，

xhxkx≈xhkx， xyxy≈yxyx.（3）

證明? 引入下列對(duì)合幺半群K0，：

K00efef1

000000

ef000efef

e0efeefe

f000ff

10efef1

x0effe1

其中

K0=e，f：e2=e，f2=f，fe=0∪{1}，

且運(yùn)算“”由映射（e，f）（f，e）誘導(dǎo).因?yàn)镵，模理想{0，fe}之后同構(gòu)于K0，，所以VarK0，VarK，.注意到從K，到K0，×K0，的映射

0（0，0），? ef（ef，0），? fe（0，ef），

e（e，f），f（f，e），1（1，1）

是一個(gè)嵌入，所以VarK，=VarK0，，故VarK=VarK0.

性質(zhì)（i）成立是因?yàn)镵0，是非有限基的［6］，而性質(zhì)（ii）成立是因?yàn)镵0的等式可以由（3）公理化；具體細(xì)節(jié)參見文獻(xiàn)［18］的命題3.2（a）.? 】

設(shè)X是可數(shù)無限字母表且X*={x*：x∈X}是與X不交的X的一個(gè)復(fù)制.稱X∪X*的元素為變?cè)?字母表X上的自由對(duì)合幺半群是自由半群（X∪X*）+加上空集并且?guī)в幸辉\(yùn)算“*”，其中對(duì)任意x∈X，x1，x2，…，xn∈X∪X*∪{}，有

（x*）*=x， *=，

（x1x2…xn）*=x*nx*n-1…x*1.

稱（X∪X*）+∪{}中的元素為字，而X+∪{}中的字為單純字.字w的內(nèi)容記作con（w），是w中出現(xiàn)的變?cè)募?

顯然每一個(gè)字w∈（X∪X*）+都可寫成

w=xα11xα22…xαnn，

其中x1，x2，…，xn∈X，α1，α2，…，αn∈{1，*}；這個(gè)字w的單純投影是指單純字

=x1x2…xn.

字w中的變?cè)獂∈X∪X*是線性的，如果w=uxv，其中u，v∈（X∪X*）+∪{}，con（uv）.字w中線性變?cè)募嫌涀鱨in（w）.

引理2? 令w1≈w2是K，*的任一等式且w1，w2∈（X∪X*）+，則

（i）con（1）=con（2）;

（ii）lin（w1）=lin（w2）.

證明? （i）假設(shè)存在某個(gè)變?cè)獂∈con（1）＼cos（2）.令φ：XK為將x映射到0而將其他變?cè)成涞?的替代，則φ（w1）=0，φ（w2）=1，矛盾.因此，這樣的變?cè)獂不存在，故con（1）=con（2）.

（ii）假設(shè)存在某個(gè)變?cè)獂∈lin（w1）＼lin（w2）.不失一般性，設(shè)x∈X，則w1=u1xv1，其中u1，v1∈（X∪X*）+∪{}并且xcon（u1v1）.由（i）可知x∈con（2），因此在w2中有以下兩種可能：

1）w2=…xα1…xα2…，其中α1，α2∈{1，*}；

2）w2=u2x*v2，其中u2，v2∈（X∪X*）+∪{}并且xcon（u2v2）.

令φ：XK為將x映射到ef而將其他變?cè)成涞?的替代，則φ（w1）=ef，φ（w2）∈{0，fe}，矛盾.因此，這樣的變?cè)獂不存在，故lin（w1）=lin（w2）.? 】

命題4 ?對(duì)合幺半群K，*的等式可以由（1），（3）式和以下等式集公理化：

x*x*≈x2， x*x≈x2， xx*≈x2，

x*yx*≈xyx， x*yx≈xyx，

xyx*≈xyx.（4）

證明? 根據(jù)命題3（ii），對(duì)合幺半群K，*滿足等式集（3）.容易驗(yàn)證K，*也滿足等式集（4）.因此，K，*的等式可以由{（1），（3），（4）}∪Σ公理化，其中Σ是由（X∪X*）+中的字構(gòu)成的等式的集合.

設(shè)w1≈w2是Σ中的任一等式.假設(shè)w1≈w2中包含一個(gè)非單純變?cè)獂*∈X*，則由引理2（i）可知x∈con（1）=con（2）.對(duì)于每個(gè)i∈{1，2}，設(shè)w′i是將wi中每個(gè)x*的符號(hào)“*”移除而得到的字，那么有以下兩種可能：

1）x*在w1或w2中是線性的，則由引理2（ii）可知，x*∈lin（w1）=lin（w2），故對(duì)于每個(gè)i∈{1，2}，存在ui，vi∈（X∪X*）+∪{}，使得wi=ui x*vi，其中xcon（uivi）.于是w′i=uixvi.因此很容易得出{（1），w1≈w2}和{（1），w′1≈w′2}定義了相同的簇.

2）x*在w1和w2中是非線性的，則利用等式集（4）可以將每個(gè)x*的符號(hào)“*”移除.因此， {（4），w1≈w2}和{（4），w′1≈w′2}定義了相同的簇.

因此在任何情況下，如果將Σ中的等式w1≈w2的每個(gè)非單純變?cè)獂*的符號(hào)“*”移除，那么{（1），（3），（4）}∪Σ仍然可以公理化K，*中的所有等式.

上述論證可以重復(fù)應(yīng)用于Σ中所有等式的所有非單純變?cè)?換句話說，如果將Σ的所有等式中出現(xiàn)的符號(hào)“*”均消除，那么{（1），（3），（4）}∪Σ仍然可以公理化K，*中的等式.因此，可以假定Σ中的等式都由單純字組成，故也是幺半群K的等式.再根據(jù)命題3（ii），Σ中的每個(gè)等式都是（3）的后承集.因此，{（1），（3），（4）}∪Σ和{（1），（3），（4）}定義了相同的簇.? 】

3? 幺半群中最小的變色龍

定理1? 6階變色龍K是幺半群中階數(shù)最小的一個(gè).

證明? 注意到，5階對(duì)合幺半群K0，是非有限基的［6］，它的約簡(jiǎn)K0沒有不同于“”的其它對(duì)合運(yùn)算，所以K0不是變色龍.此外，每一個(gè)不與K0，同構(gòu)且階數(shù)小于等于5的對(duì)合幺半群都是有限基的［19］，因此，在階數(shù)小于等于5的幺半群中不存在變色龍.? 】

參考文獻(xiàn)：

［1］? OATES S，POWELL M B.Identical relations in finite groups［J］.Journal of Algebra，1964，1（1）：11.

［2］? KRUSE R L.Identities satisfied by a finite ring［J］.Journal of Algebra，1973，26（2）：298.

［3］? LVOV I V.Varieties of associative rings I［J］.Algebra and Logic，1973，12（3）：150.

［4］? BAHTURIN Y A，OLSHANSKII A Y.Identical relations in finite Lie rings［J］.Mathematics of the USSR-Sbornik，1975，25（4）：507.

［5］? MCKENZIE R N.Tarskis finite basis problem is undecidable［J］.International Journal of Algebra and Computation，1996，6（1）：49.

［6］? GAO M，ZHANG W T，LUO Y F.A non-finitely based involution semigroup of order five［J］.Algebra Universalis，2020，81（3）：Art.31，14 pp.

［7］? JACKSON M，VOLKOV M V.The algebra of adjacency patterns：Rees matrix semigroups with reversion［C］//Fields of Logic and Computation，Lecture Notes in Computer Science，6300，Berlin：Springer，2010：414.

［8］? LEE E W H.Non-finitely based finite involution semigroups with finitely based semigroup reducts［J］.Korean Journal of Mathematics，2019，27（1）：53.

［9］? LEE E W H.Varieties of involution monoids with extreme properties［J］.Quarterly Journal of Mathematics，2019，70（4）：1157.

［10］? LEE E W H.Finitely based finite involution semigroups with non-finitely based reducts［J］.Quaestiones Mathematicae，2016，39（2）：217.

［11］? LEE E W H.Finite involution semigroups with infinite irredundant bases of identities［J］.Forum Mathematicum，2016，28（3）：587.

［12］? LEE E W H.Equational theories of unstable involution semigroups［J］.Electronic Research Announcements in Mathematical Sciences，2017，24：10.

［13］? LEE E W H.Intervals of varieties of involution semigroups with contrasting reduct intervals［J］.Bollettino dell'Unione Matematica Italiana，2022，15（4）：527.

［14］? LEE E W H.Varieties generated by unstable involution semigroups with continuum many subvarieties［J］.Comptes Rendus Mathématique，2018，356（1）：44.

［15］? CRVENKOVIC S，DOLINKA I.Varieties of involution semigroups and involution semirings：a survey［J］.Bulletin of Society of Mathematicians.Banja Luka，2002，9：7.

［16］? LEE E W H.Advances in the Theory of Varieties of Semigroups［M］.Frontier in Mathematics，Cham：Birkhuser，2023.

［17］? ZHANG W T，LUO Y F.A new example of a minimal nonfinitely based semigroup［J］.Bulletin of the Australian Mathematical Society，2011，84（3）：484.

［18］? EDMUNDS C C.On certain finitely based varieties of semigroups［J］.Semigroup Forum，1977，15（1）：21.

［19］? HAN B B，ZHANG W T，LUO Y F.Finite basis problem for involution monoids of order five［J］.Bulletin of the Australian Mathematical Society，2023，doi：10.1017/S0004972723000989.

（責(zé)任編輯? 馬宇鴻）