基于聯合控制仿真的主動式橫向穩定桿控制策略研究

丁義蘭

長安馬自達汽車有限公司,江蘇 南京 210094

0 引言

相較于其他車輛,越野車質心高、尺寸大、裝載質量重,最易發生側傾,甚至誘發側翻。為了解決該問題,國內外學者進行了很多研究,其中黃康 等[1]、趙樹恩 等[2]、張瑞棟[3]研究了主動橫向穩定桿對車輛的防側傾技術,王國麗 等[4]、孟愛紅 等[5]以及劉少軍 等[6]研究了主動懸架對車輛側翻性能的影響,并進行了仿真分析,但對于橫向穩定桿對車輛側傾甚至側翻性能的影響,鮮有人研究。

橫向穩定桿是懸架中的一個部件,在車輛轉彎時,橫向穩定桿桿體發生扭轉,桿身變形產生的彈力就會阻止車輪抬起,預防側傾,但實際應用中,桿身的變形有限,難以滿足復雜多變的工況要求。

本文正是在原車輛橫向穩定桿的基礎上,設計了一款主動式橫向穩定桿系統,它將原桿件從中間斷開,在中間加裝了一個激勵器系統,并對該系統設置了4種控制策略,可以根據車況的要求,實時調節車輛所需的防側傾力矩。為了驗證該系統控制策略的有效性,先利用ADAMS建立整車剛柔耦合動力學模型,再利用MATLAB/Simulink的模塊化功能,建立相應控制策略的控制模型,最后通過接口相連進行聯合控制仿真,驗證該系統對整車側傾甚至側翻的改善程度。

1 基于主動式橫向穩定桿的整車剛柔耦合動力學模型的搭建

1.1 基于被動式整車剛柔耦合模型的建立

本文建模所需的越野車3D和詳細參數,均為某合作廠家提供。根據提供的參數,利用轉動副、固定副、襯套等,分別將該車的動力傳動系統、前后懸架、前后被動式橫向穩定桿、前后車輪、轉向系統、車身與地面等部件,在ADAMS中逐一進行簡化連接,其中忽略了與本研究無關的制動系。

另外,因本文主要研究對象為橫向穩定桿,在實際應用中,桿件自身可以承受部分變形,故選用結構和力學響應性更高的柔性體更符合實際情況。本文利用HyperMesh軟件,來算出橫向穩定桿的固有頻率和模態,并將其模態結果進行合成,獲得其柔性化的模型,并將該模型導入到ADAMS軟件中。最終,將各模塊的簡化模型和橫向穩定桿柔性化模型進行關聯,得到整車剛柔耦合動力學模型,如圖1所示。

圖1 整車剛柔耦合動力學模型

1.2 基于主動式整車剛柔耦合動力學模型的建立

以被動式整車剛柔耦合模型為基礎,其余零件不變,只將原橫向穩定桿件一分為二,并在中間設立一個變量力矩,該力矩是依靠MATLAB/Simulink中的輸入來控制(接口相連),用于抵抗車身的側傾,相當于激勵器的作用(ADAMS簡化模型)。

1.3 模型的驗證

依據GB/T 6323.6—1994的要求進行實車穩態回轉試驗,獲得的數據與仿真試驗的數據進行對比,試驗的質心軌跡和仿真獲得的質心軌跡差距極小,近似于重合,且前后軸的側偏值分別為0.78(°)/(m/s2)和0.82(°)/(m/s2),因此,可以確定該整車剛柔耦合模型準確度較高。

2 主動式橫向穩定桿系統的控制策略研究

2.1 被動式橫向穩定桿的參數計算

主動式橫向穩定桿系統以原車型的被動式橫向穩定桿為基礎,不改變其安裝位置和原桿件的剛度、直徑、彎曲性狀,只是將橫向穩定桿從中間斷開,加裝激勵器,故被動式橫向穩定桿的相關參數可根據廠家提供的參數進行計算,其中,本文中被動式橫向穩定桿的兩端位移工作范圍為(-40,40)mm。

通過以下的公式進行測算:

(1)

式中:φ1為車身側傾角;f為穩定桿端點距離;ay為側向加速度;a為剛度比(前后側傾);Maf為激勵器輸出的總側傾力矩;Ws為車輛的簧上質量;hs為車輛質心距側傾中心的距離;kφf為前輪側傾剛度;kφr為后輪側傾剛度。

可計算出原桿件自身扭轉變形能提供的側傾角和側向加速度如下。

φmax=3.81°,φmin=0.45°,ay min=0.05 g

(2)

式中:φmax為車身最大側傾角;φmin為最小側傾角;ay min為最小傾向加速度。

橫向穩定桿通過自身的扭轉變形,為整車提供一個抑制側傾的力矩,但由計算可知,該桿件自身的最大側傾角僅為3.81°,一旦超過該限值,桿體就會因發生塑性變形而失效。而本文研究的主動式橫向穩定桿,其激勵器會在整車側傾角大于原桿件最小側傾角0.45°時開始工作,根據所制定的控制策略判斷系統此時所需的力矩,驅動電機,為整車系統提供一個新的抗側傾力矩,有效防止車輛的側翻,避免該桿件發生塑性變形。

激勵器的組成如圖2所示。

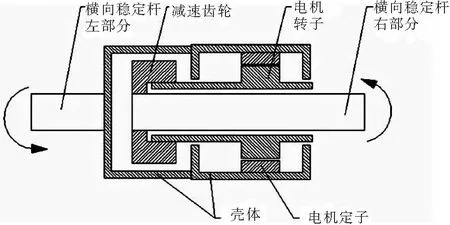
圖2 激勵器剖面圖

2.2 主動式橫向穩定桿系統控制策略的確定

控制策略是主動式橫向穩定桿系統的核心,本文研究的主動式橫向穩定桿系統除了包含原桿件和電機激勵器,為了實現其控制策略,還設有控制單元ECU,此外還包含各種傳感器,如力矩傳感器、側向加速度傳感器及車身側傾角傳感器等。電控ECU基于來自側向加速度傳感器和車身側傾角傳感器的數值,來確定車身的側傾狀況,并根據側傾狀況計算所需的扭矩,以驅動主動式橫向穩定桿系統,從而達到改善車輛的側傾穩定性的目的。

為了更好地研究該系統,首先得確認車輛行駛時的實況,本文總結了3種常見行車工況:水平路面,車輛直線行駛;水平路面,車輛轉彎;左右兩邊傾斜的路面,無轉彎,因車輛左右車輪引起的傾斜。

依據以上3種工況,制定主動式橫向穩定桿系統的控制原理(見圖3)。

圖3 主動式橫向穩定桿系統的控制原理圖

在正常行車中,確保所有傳感器均在工作狀態,為了實現有效的控制,結合上文所研究的原桿件的最大側傾角、最小側傾角和側向加速度等相關參數,得到以下的控制策略。

1)若控制單元檢測到的側傾角φ小于0.45°,則判定為車輛無側傾,直線行駛。此時調用的是第1種控制策略,即此時控制電機主動力矩為0,桿體左右2部分分離,懸架剛度降低,乘坐舒適性大大改善。

2)若控制單元檢測到的側傾角φ大于等于0.45°,ay大于等于0.05 g,則判定車輛轉彎中。調用的控制策略如圖4所示,即將側向加速度和抗側傾力矩作為輸入量,通過ECU計算出理論側傾角,并將理論側傾角與傳感器測得側傾角的差值作為反饋,不斷修正,直至該差值小于0.45°,固定電機的施加力矩M。

圖4 第2種控制策略流程

3)若控制單元檢測到的側傾角φ大于等于3.81°,ay小于0.05 g,判定該車無轉彎,行駛在左右存在傾斜的路面;或者由左右車輪引起的傾斜,此時已超過側翻的閥值有側翻危險,可調用第3種策略,即控制激勵電機,將其輸出的力矩固定在最大值,進行持續工作,直至車身回正。

4)若控制單元檢測到的側傾角大于0.45°,小于3.81°,ay小于0.05 g,判斷該車輛處于側傾狀態,但未到側翻的閥值,調用的控制策略如圖5所示,即將側向加速度和側傾角作為輸入量,通過ECU計算出系統此刻所需的力矩,并將車身的側傾角作為反饋,不斷修正施加系統的力矩,直至側傾角小于0.45°為止。

圖5 第4種控制策略

3 基于聯合控制仿真的主動式橫向穩定桿控制策略的驗證

3.1 建立基于主動式穩定桿件的數學模型

為了便于在MATLAB/Simulink中調用模塊化功能來建立對應的控制策略,需要先建立整車側傾的數學模型,確立與整車側傾相關的3個參數之間的關系,即整車側傾角、側傾加速度、側傾力矩三者之間的關系。

首先,假定車輛正在勻速轉彎中,整車的受力示意圖如圖6所示。

圖6 車輛勻速圓周運動中轉彎受力示意圖

由整車動力學簧上質量的平衡方程,可推導出如下傳遞函數:

(3)

式中:Maf為激勵器輸出的總側傾力矩;maf為電機產生的扭轉力矩;b1/l1為縱臂、橫向臂的位移率(橫向穩定桿);α為剛度比(前后側傾)。另外,試驗測出:μ=ay,未知量只有φ、ay及Maf,其余數值均為合作方提供或者試驗測出的已知量。

3.2 聯合仿真模型的建立

針對上文制定的控制策略和建立的傳遞函數,運用ADAMS/MATLAB/Simulink聯合仿真,驗證控制策略的完整性,并根據結果不斷進行修正和更新該系統的設計參數。

先通過ADAMS軟件建立基于主動式橫向穩定桿的整車動力學模型,同時依據前文所制定的控制策略和傳遞函數,在MATLAB/Simulink中建立了控制系統,并通過接口將2個軟件系統中的模塊聯接起來,最后基于ADAMS和MATLAB/Simulink,建立了整車的聯合控制仿真模型,來驗證該系統控制策略是否可行。另外,車輛質心側向加速度和側傾角作為ADAMS中的輸出量,它同時也是Simulink中的輸入信號,而電機的主動轉矩作為Simulink中的輸出量,它也是ADAMS中的輸入量。

3.3 主動式與被動式橫向穩定桿對整車側傾性仿真結果分析

基于上文建立的ADAMS和MATLAB/Simulink的整車模型,依據國標和美標的行業標準,分別選取與整車側傾相關的2種試驗進行驗證,即穩態回轉及魚鉤試驗,并將其與被動式穩定桿的數據進行比較,來確認該系統制定的控制策略是否可行,并確認主動式橫向穩定桿系統是否對車輛側傾的改善有所幫助。

3.3.1 穩態回轉試驗

從圖7～8可知,穩態回轉試驗中(根據國標穩態回轉試驗方法,在相同時間,2種條件下的速度相同),在低速階段,安裝主動式橫向穩定桿系統的側向加速度和側傾角更加穩定,接近0值,但在高速階段,該系統相對于安裝被動式橫向穩定桿的系統,無論是側向加速度還是側傾角,降幅明顯,對車輛的整車側傾性改善明顯。

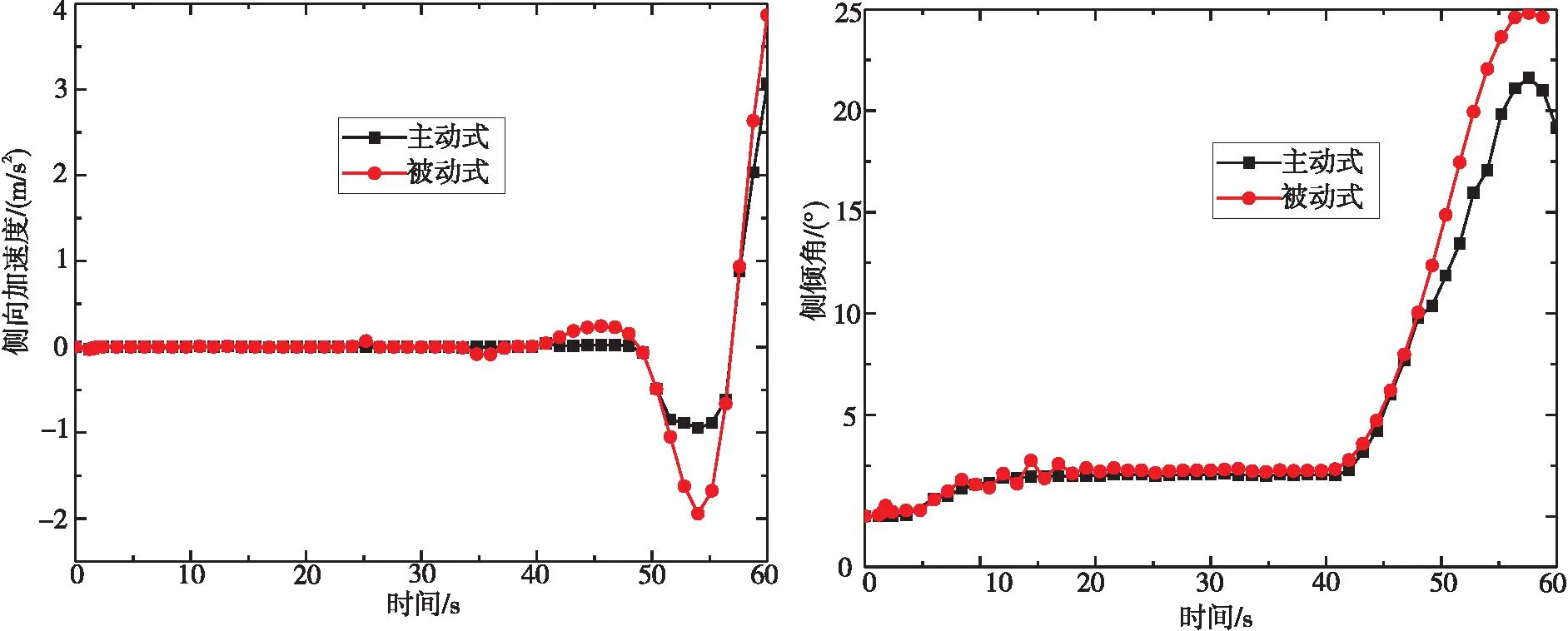
圖7 穩態回轉試驗2種條件下側向加速度曲線圖 圖8 穩態回轉試驗2種條件下側傾角曲線圖

3.3.2 魚鉤試驗

如圖9～10所示,魚鉤試驗中(模擬車輛行駛一段行程偏航后,方向快速回正的過程,美標),在方向回正的過程中,安裝主動式橫向穩定桿系統的側向加速度降幅明顯,峰值較安裝被動式橫向穩定桿的系統,降低了50%,而側傾角峰值降低了25%,可以得出本文研究的主動式橫向穩定桿系統可以很顯著降低車輛急速回正時的側翻風險。

圖9 魚鉤試驗2種條件下側向加速度曲線圖 圖10 魚鉤試驗2種條件下側傾角曲線圖

4 結論

本文主要研究主動式橫向穩定桿對某款越野車的側傾的影響,先通過ADAMS中建立了基于該系統的整車剛柔耦合動力學模型,然后詳述了該系統的4種控制策略,且在MATLAB/Simulink中建立相應的控制模型,最后進行聯合控制仿真,得到以下結論。

1)制定的主動式橫向穩定桿的控制策略是有效的。穩態回轉試驗和魚鉤試驗中,隨著時間的增加,該控制策略響應快、靈敏度高,能顯著降低車身的角速度和側向加速度。

2)主動式橫向穩定桿系統相較于被動式穩定桿,對車身側傾狀態改善明顯,有很大的研究空間。