基于模型的動力電池SOC估計方法研究進展

侯書增，伍志明，程 雪，翟 博

(四川輕化工大學機械工程學院，四川宜賓 644000)

隨著動力電池硬件技術的日臻成熟，負責汽車行駛安全的電池管理系統(battery management system，BMS)能力的提升已成為推動燃油汽車向電動汽車加速轉型的關鍵。BMS 是電動汽車中重要的主動安全系統，通常由許多算法、模型和控制信號驅動傳感器、芯片和安全設備來實現對電池的控制與管理[1]。其中電池荷電狀態(state of charge，SOC)估計是BMS 中核心功能之一，可為電池安全控制、充/放電保護和整車能量管理等功能提供重要參考[2]。電池的SOC值無法直接得到，只能通過它與外在物理參數(電壓、電流、電阻等)間的關系來進行間接估算。由于此種關系具有很強的非線性，因此精確地進行在線估計面臨著很大的挑戰。針對動力電池SOC精確估計的需求，本文對電池模型、模型參數辨識方法和SOC估計方法進行總結歸納和優劣勢分析，并統計了國內主流BMS 生產商關于SOC算法的應用與開發研究。

1 動力電池模型與參數辨識

1.1 動力電池模型

動力電池模型旨在模擬和仿真電池的外特性，主要有兩類模型：電化學模型(electrochemical model，EM)和等效電路模型(equivalent circuit model，ECM)。EM 模型是通過偏微分方程來解釋電池內部的反應狀態[3]。EM 包括準二維(pseudo twodimensional，P2D)模型、單粒子模型(single particle model，SPM)、集總粒子模型(lumped particle model，LPM)和多物理耦合(multiphysical-coupling，MC)模型等。P2D 模型是根據多孔電極理論和溶液濃度理論建立的。由于電池建模參數多、電池材料參數的不可測性，導致該模型在線計算困難，難以實際應用。SPM 是在P2D 模型基礎上，通過簡化降階，將偏微分方程轉化為常微分方程所建立的電池模型。由于減少了不必要的參數，模型得以簡化。研究表明SPM和P2D 模型易受到電極、電勢和溫度等因素影響。LPM 模型考慮了上述因素影響，將電池組比作單個球狀粒子，用單個粒子模擬整個電池組的電化學傳輸過程，降低了計算成本，提高了模型的普適性。李等[4]對SPM 和LPM 建立了放電電壓曲線，對比發現在低倍率放電下LPM 比SPM 電壓準確度高，在高放電倍率下，LPM 模型電壓精度相對于SPM 較差。MC 模型是在EM 的基礎上耦合了電池熱和老化的影響[5]，具體模型框架如圖1 所示。目前，MC 模型的可靠性還處于探索的早期階段，電池的綜合性實驗驗證(如老化、退化實驗)工作難度大、可靠性驗證困難。

ECM 是通過極化內阻、極化電容和端電壓等電路元件構成的閉環系統來描述動力電池的外特性。ECM 包括Rint 模型、Thevenin 模型、二階RC 模型、PNGV 模型和GNL 模型等。表1 列出了模型結構和它的優缺點。

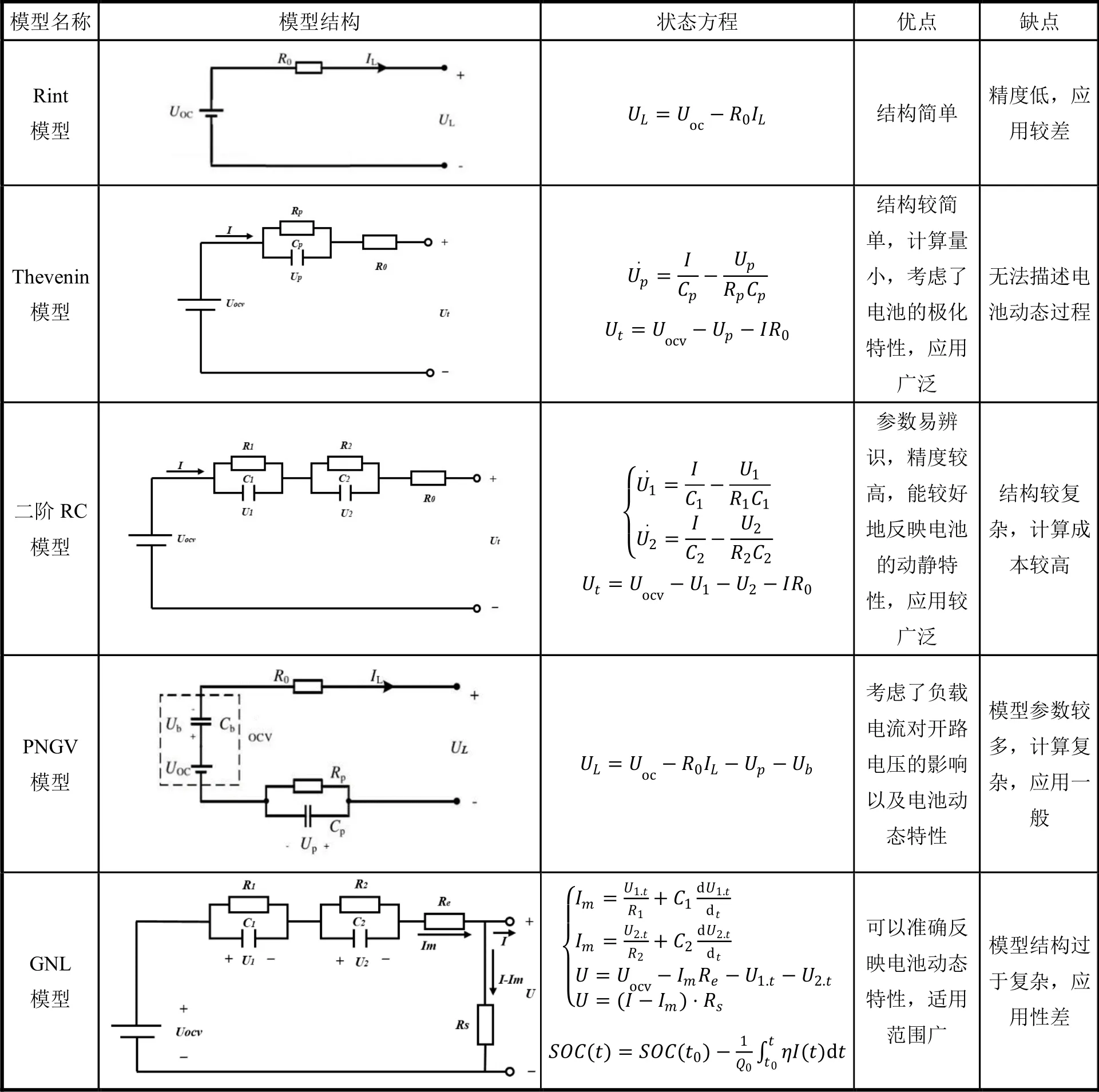
表1 常見電池等效電路模型對比

從表1 可以看出，Thevenin 模型和二階RC 模型由于可以更好地平衡模型的準確性和復雜性，目前運用比較主流。

此外，有學者開始將電化學模型與等效電路模型相結合用于電池建模。如德國布倫瑞克工業大學的學者開發了考慮電極電化學反應的拓展等效電路模型(extend equivalent circuit model，EECM)，該模型能夠實現高保真度。Kim 等[6]提出了一種改進型的組合式EECM 模型，其實驗結果較傳統ECM 估計精度更高。這表明，采用不同模型協同優化的策略是提高電池SOC估計精度的一種重要途徑。

1.2 參數辨識

參數辨識的準確性對電池模型的質量、優化和評價至關重要，因此電池模型在實際應用前必須進行參數辨識工作。圖2 所示為二階Thevenin 等效電路模型參數辨識的相關步驟。首先對電池進行混合功率脈沖特性(HPPC)測試，獲得單體電池參數值，然后利用測試結果，采用特定辨識方法完成模型參數辨識。

圖2 Thevenin等效電路模型參數辨識流程

最小二乘法是目前最常用的參數辨識方法之一。在面對多時間尺度系統時，最小二乘法存在模型參數辨識精度低、建模效果差等問題。目前，最小二乘法的改進方法正獲得國內外學者的青睞。Plett[7]提出一種加權最小二乘法，改善了電流、電壓等測量噪聲帶來的估計不準問題。王等[8]在此基礎上提出了加權遞推最小二乘法，通過引入加權因子調整遞推模型對舊數據和新數據的置信比例，實現在線跟蹤鋰電池模型參數的變化，從而提高了電池模型參數與真實值的接近程度。朱等[9]提出了一種基于分布式最小二乘法的模型參數辨識方法，研究表明其辨識精度較遞推最小二乘法提高了50%左右。任等[10]在遞推最小二乘法基礎上引入小波變換，提高了系統跟蹤能力，得到了較高精度的辨識結果，但計算時間顯著增加。這些方法仍處于實驗研究階段，還無法獲得實際應用。

此外，研究人員通過智能算法進行了大量的電池模型參數辨識工作，例如粒子群算法(particle swarm optimizer，PSO)和遺傳算法(genetic algorithm，GA)。PSO 具有記憶性好、參數少和原理簡單易實現等特點。GA 相較于PSO，具有共享性好、收斂性成熟和應用廣泛等特點。黃等[11]提出了一種改進型PSO 算法辨識ECM 模型參數，能夠激勵粒子和種群實現最優位置持續更新。徐等[12]采用GA 辨識出EM模型參數，總體上能夠保證電池模型的精度要求，但模型的電壓輸出與實際電池電壓仍存在一定偏差。通過實驗結果對比發現，智能算法在參數辨識時具有一定的優勢，辨識得到的結果能模擬電芯的實際特性。但是，智能算法辨識的結果具有隨機性，會導致最終辨識結果不同，從而出現收斂精度較低等問題，并且配置電池模型參數上下邊界不合理時，辨識的結果將產生較大的誤差。

2 動力電池SOC 估計方法

2.1 直接估計法

直接估計法是通過直接測量電池的一些外部物理參數來計算電池SOC。這類算法主要包括開路電壓法(open circuit voltage，OCV)、安時積分法(currentsensor integration，CSI)、內阻法(internal resistance，IR)和阻抗譜法(impedance spectroscopy，IS)。

OCV法是利用SOC與電池開路電壓之間的一對一映射關系進行SOC估計。通過脈沖充放電實驗可獲得動力電池的OCV-SOC關系，當電池工作時，利用其內部傳感器檢測電池的端電壓值，然后通過系統存儲的OCV-SOC關系進行SOC[13]估算。需要指出的是，不同電池所具有的OCV-SOC關系也不同，且不同溫度狀態，不同生命周期也會影響SOC的估計誤差。圖3 為三元鋰電池和磷酸鐵鋰電池在20 ℃下的OCV-SOC關系圖，從圖中可以看出兩類電池的OCV-SOC關系差別相對較大。圖4 為2 Ah 18650 電池在不同溫度下的OCV-SOC關系圖，從圖中可以看出，溫度對電池的OCV-SOC關系影響并不顯著。

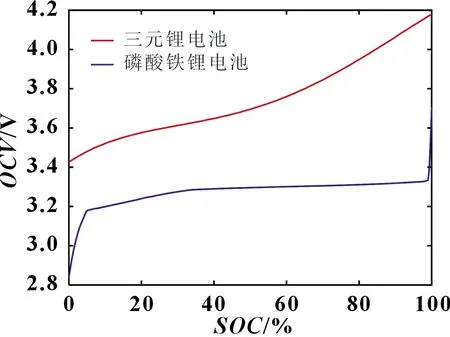
圖3 三元鋰電池和磷酸鐵鋰電池在20 ℃下的OCV-SOC關系曲線

圖4 18650電池在不同溫度下的OCV-SOC關系曲線

實際應用中，電動汽車行駛過程中檢測到的端電壓是放電電壓，由于電池的極化作用，電池端電壓存在緩慢上升的過程，電池靜置一段時間后才能得到開路電壓。由于電池無法快速達到相對穩態這一條件，因此OCV法不適用于SOC在線實時估計，目前主要運用于實驗室。

CSI 法是目前在BMS 中應用最廣的SOC估計方法。當電池以一定的倍率放電時，任意t時刻的SOC值為剩余電池容量與電池額定容量的比值[14]，CSI 由如下公式表達：

式中：Qu為剩余電池容量；Qn為電池額定容量。

Qu由下式計算得出：

假設電池的初始SOC值為SOC(t0)，由式(1)可得：

式中：I為電流，放電時為正，充電時為負。

CIS 法主要有兩個局限：其一是它的SOC值計算要從一個初始SOC值開始，這個初始SOC必須是精準的；其二是因傳感器精度、電流和采樣頻率而產生的誤差會隨著時間的推移而累積，從而使估計結果的誤差越來越大，該方法不具有更新電池初始容量的能力，不能解決電池老化和自放電等問題。

IR 法和IS 法是依據對電池增加周期變化的電流量，推算出電池的內阻或阻抗譜，然后跟據電池內阻和阻抗譜測算電池SOC。上述方法對傳感器靈敏度要求較高，在BMS 設計開發中采用較少。

2.2 機器學習法

機器學習法具有記憶性和參數共享等優點，對非線性系統學習具有一定優勢。該方法主要包括神經網絡、粒子群算法、遺傳算法和支持向量機等。表2 總結了近年來機器學習方法在電池SOC估計方面的一些研究成果。

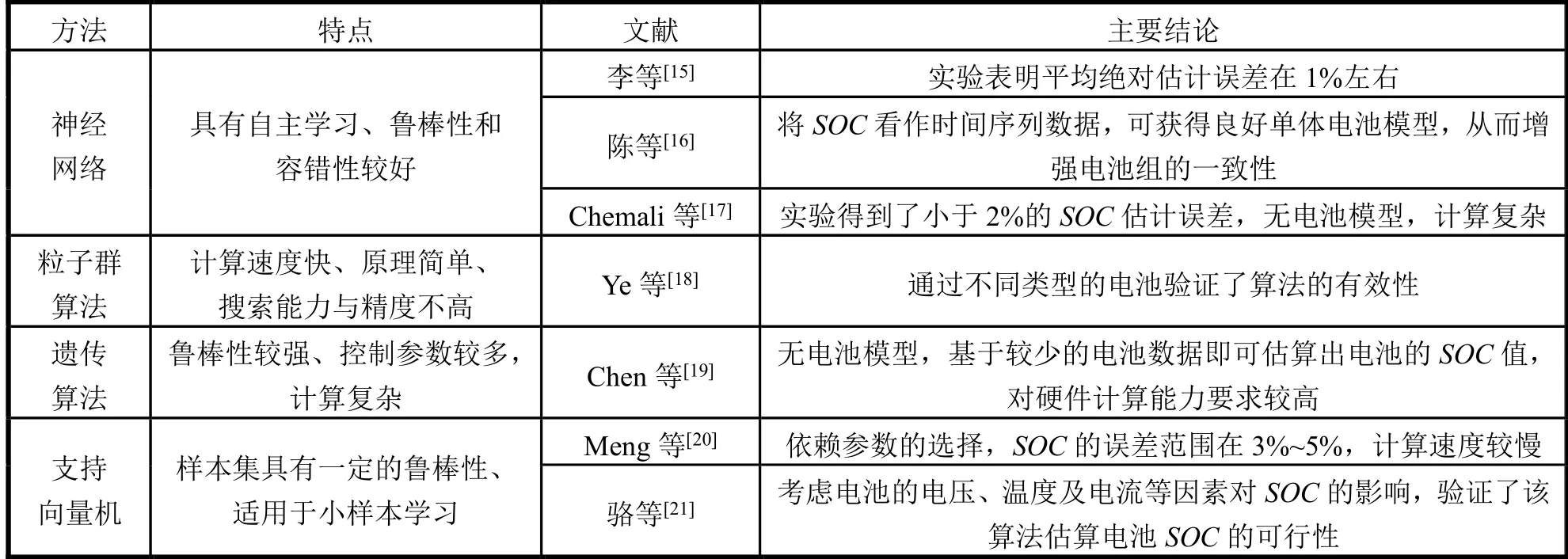
表2 常見機器學習方法在電池SOC 估計方面的研究成果

從表2 可以看出，機器學習方法表現出較強的學習能力、快速的收斂速度，可以在無數學模型的情況下運行，這對于電池SOC估計是非常理想的，但是此類方法對電池樣本集要求較高，計算量大，不利于故障診斷。

2.3 基于模型的狀態估計法

基于模型的狀態估計法是在電池模型的基礎上，借助濾波器類算法來實現SOC估計。濾波器主要包括擴展卡爾曼濾波器(EKF)、H 無窮濾波器(HIF)、粒子濾波器(PF)和滑模觀測器(SMO)等。

EKF 是一種較好的自適應算法，被廣泛應用于包括電池在內的許多系統的狀態估計和壽命預測。EKF 可以解決非線性系統的最優估計問題，具有計算效率高、噪聲抑制能力強、穩定性好等優點。但是EKF 計算密集復雜，通常需要額外的參數或電池模型，影響了估計精度。

HIF 是為了處理含有模型結構、模型參數的不確定和系統噪聲等問題而提出的。潘等[22]將電池溫度、容量和電阻作為系統變量，用切線法對模型優化，通過HIF 對電池SOC進行估計，獲得了良好的估計精度。但是該算法無法避免因系統狀態和模型不確定性所造成的電池SOC估計不精準問題。

PF 算法是一種統計濾波算法。它通過粒子集合表示系統狀態變量的分布，可應用于任何形式的狀態空間模型，為求解系統狀態估計的概率密度分布提供了一種新的思路。在模型預測估計中，若樣本集過多，會出現重復采樣，從而增大計算復雜度。因此，PF在電池SOC估計上一般都是通過優化改進使用。

SMO 是為存在不確定性的非線性對象提供魯棒控制器的一種策略。Chen 等[23]通過改進SMO 估計算法，驗證了SMO 可以適應電池電流劇烈變化的充放電工況，并且魯棒性較好，但SMO 算法占用計算資源較多且估計結果可能存在較大的誤差和不確定性，該算法還有待進一步探索。

2.4 聯合估計法

動力電池SOC的聯合估計法就是將基于模型的狀態方程估計法和另外一種或幾種用于電池參數估計的方法相結合。它結合了幾種算法的優勢，抑制了各自的缺點，是目前SOC估計方法研究的熱點。表3 介紹了近年來SOC聯合估計方法所取得的主要研究成果。

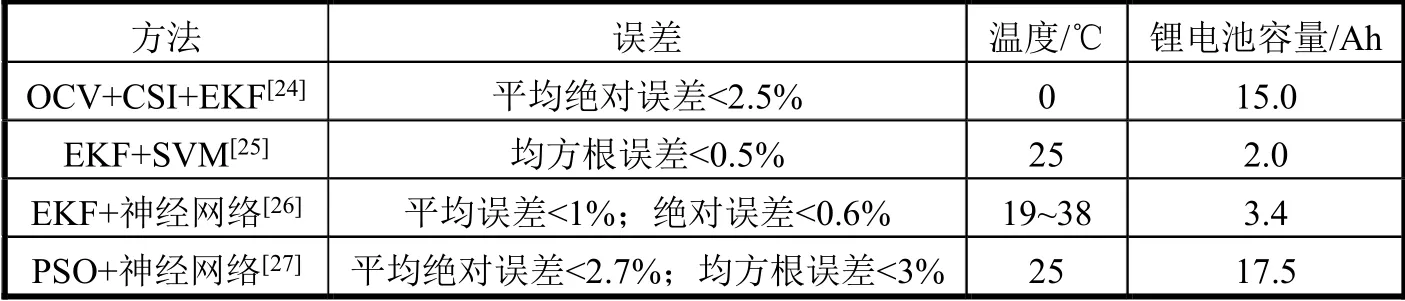
表3 聯合估計法在電池SOC 估計方面的應用研究

從表3 可以看出，聯合估計總體上獲得了較好的估計精度，分析計算誤差均在3%以內。特別是EKF+SVM、EKF+神經網絡的聯合方法誤差范圍較小。這進一步表明EKF 可以抑制噪聲，較好地處理非線性系統。但是，EKF 需要較高精度的電池模型。神經網絡對模型精度要求較低，能夠較好地解決電池模型不精準問題。采用EKF 和神經網絡的聯合估計方法，克服了模型依賴性強、濾波器容易發散和電池模型計算量大的問題，體現了聯合估計法的優越性，但是離實際應用還有待進一步拓展研究。在面對電池參數、溫度、單體電池成組后的不一致性和電池內部微小短路等情況時，聯合估計仍存在局限性。

3 動力電池SOC 估算功能的應用研究

目前國內主流BMS 生產商的SOC估算技術一般采用安時積分法、開路電壓法和基于卡爾曼濾波器等算法進行狀態估計，同時結合電池模型、電化學特性等因素進行修正和校準，并且SOC估算精度大多保持在5%左右，如表4 所示[28-29]。此外，BMS 廠商也在不斷創新SOC估算算法，如借助物聯網、人工智能等新技術，以提高SOC估算的準確度和可靠性。

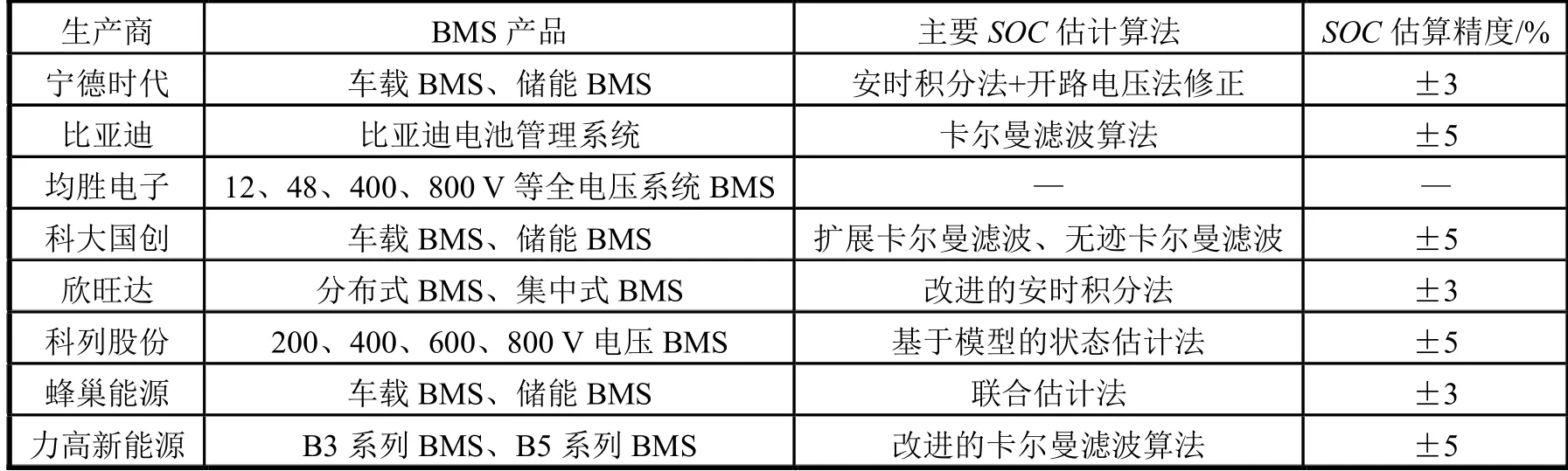
表4 國內主流BMS 生產商SOC 估算技術情況

4 總結與展望

動力電池SOC估計的評價標準最主要的特點是估計精度和計算復雜度。雖然近年來國內外學者在這方面取得了許多研究進展，但在面對比實驗室條件更為復雜的實際工程應用時，這些技術仍然顯得力不從心。因此，在未來尚有許多可以改進和探索的方向。

(1)采用先進的電池建模和仿真技術，以便更準確地預測電池的行為和狀態。

(2)在電池模型參數辨識研究方面，以最小二乘法為基礎的改進策略仍將是未來重要的研究方向之一。此外，智能算法由于收斂性、參數設置等問題，距離實際應用還存在一定困難。

(3)對SOC估計算法進行多源信息融合，如結合溫度、電壓、電流和外部環境等多種信息，實現對電池組狀態的全方位、多角度監測和評估，以提高估算精度和可靠性。

(4)引入深度學習、機器學習等人工智能技術，實現對電池組狀態的自主學習和調整，以適應不同電池和使用環境，提高系統的靈活性和智能化水平。