低溫風洞中液氮液滴的破碎特性模擬研究

苗慶碩,魏震,陳佳軍,張海洋,鐘富豪,鄭勉,劉秀芳

(1. 西安交通大學能源與動力工程學院,710049,西安;2. 中國空氣動力研究與發展中心設備設計及測試技術研究所,621000,四川綿陽)

基于相似理論進行的風洞模擬試驗是探究飛行器氣體動力學性能的核心技術手段。由于模型試驗固有的尺度效應以及試驗條件的限制,常規風洞所能達到的雷諾數模擬能力有限,無法滿足新型飛行器的氣動試驗需求。采用液氮噴霧冷卻方法實現氣流降溫是提高風洞試驗雷諾數[1-2]的最佳方案之一。低溫風洞中的液氮噴霧冷卻過程是一個復雜的多變量強耦合過程,受到液滴破碎、液滴碰撞、液滴撞壁等行為過程[3-5]的影響,其中,液滴的變形與破碎涉及氣液界面的失穩和多相流體的湍流混合,機理異常復雜。在高速氣流剪切力的作用下,液氮液滴的形態演變及熱動力學特性直接影響著液氮噴霧霧場的發展,進而決定低溫風洞的流場品質。因此,深入研究低溫風洞中液氮液滴的破碎特性,揭示液氮液滴的破碎機理顯得尤為重要。

氣流中液滴破碎的控制參數主要為韋伯數(We)和奧內佐格數(Oh),分別表征氣動力、液相黏性力與表面張力的相對大小,表達式如下

(1)

(2)

式中:ρl、ρg分別表示液體和氣體的密度;μl表示液體黏度;σ表示表面張力系數;U0表示氣流初始速度;d0表示液滴初始直徑。

大量研究表明,We對液滴破碎起促進作用,Oh對液滴破碎起抑制作用[6-7],且當Oh<0.1時,液滴破碎模式基本不受其影響,主要由We決定[8]。國內外學者將不同液滴破碎模式進行分類,指出隨著We的增大,液滴破碎模式可以分為振蕩破碎、袋狀破碎、多模式破碎(中間態破碎)、剪切破碎和爆炸破碎等5大類,而多模式破碎又可以進一步分為袋狀雄蕊破碎、袋狀羽化破碎、雙袋式破碎、多袋式破碎、羽化剪切破碎等[8-16]。

當液滴位于氣流中時,形態會發生變化。定義變形系數C=dcro/d0,是表征液滴形態變化的重要參數,其中dcro表示發生變形的液滴在垂直氣流方向的徑向長度。此外,為了便于比較,通常對液滴破碎過程中的時間參數進行無量綱化處理,具體表達式如下

(3)

式中:T表示無量綱時間;t表示實際時間。

Song等[17]探究了水滴在液滴變形階段和袋狀擴展階段變形系數的變化規律,指出袋狀結構開始產生后,變形系數增速變大。施紅輝等[18]的研究結果表明,不同破碎模式下變形系數的變化規律不同,但在液滴變形階段,其隨無量綱時間基本呈線性變化。張文英等[19]通過研究指出,當水滴發生袋狀破碎時,隨著無量綱時間的增大,水滴變形系數由線性增長轉變為二次函數增長。Zhu等[20]的模擬結果則表明,發生剪切破碎的正辛烷液滴的變形系數隨時間呈指數增長趨勢。

液滴初始破碎時間是液滴破碎特性的一個重要參數,表示液滴袋狀結構開始形成或邊緣液滴顆粒開始脫落的時間[10]。Pilch和Erdman[10]歸納了無量綱初始破碎時間與We以及Oh的關系,指出無量綱初始破碎時間隨著We的增大而減小,且隨Oh的增大而增大。Dai和Faeth[12]通過實驗研究,同樣得到了無量綱初始破碎時間隨著We的增大而減小的結論。而Hsiang和Faeth[8]的實驗結果則表明當Oh<0.1時,無量綱初始破碎時間基本不受We的影響,始終維持在1.6附近。金仁瀚等[21]發現無量綱初始破碎時間隨著We的增大呈現先減小后不變的規律。Zhu等[20]發現當液滴發生剪切破碎時,液滴初始破碎時間與初始直徑成正比,而與初始氣流速度成反比。

現有的研究主要聚焦于水滴、油滴等常溫工質液滴。相較于常溫工質液滴,低溫液氮液滴的表面張力要低得多,由于決定液滴破碎特性的關鍵特征參數We與表面張力密切相關,導致液氮液滴的變形與破碎過程或將呈現出與常溫工質截然不同的特點。因此,本文基于耦合水平集流體體積函數(coupled level-set and volume of fluid,CLSVOF)方法,構建了液氮液滴破碎模型,對比了低溫液氮液滴與常溫液滴的形態演變規律,分析了液滴變形和破碎過程中的壓力變化特征,探究了We對液氮液滴形態和變形系數的影響,最后歸納了液氮液滴的時間特性。

1 模型設置與驗證

1.1 模型設置

對復雜的液滴破碎過程進行適當簡化,忽略氣液兩相之間的相變過程,建立如圖1所示的二維液滴破碎仿真模型。選取重力加速度g=9.81 m·s-2,重力方向與氣流方向垂直,壓力速度采用壓力-隱式分裂算子(pressure-implicit with splitting of operators,PISO)耦合方法,壓力離散格式為PRESTO!,其余參數均采用對流項二次迎風差值(quadratic upwind interpolation of the convective kinematics,QUICK)格式離散。模型網格為結構化網格,采用自適應局部網格加密技術,加密標準取決于單元內液相體積分數梯度分布。

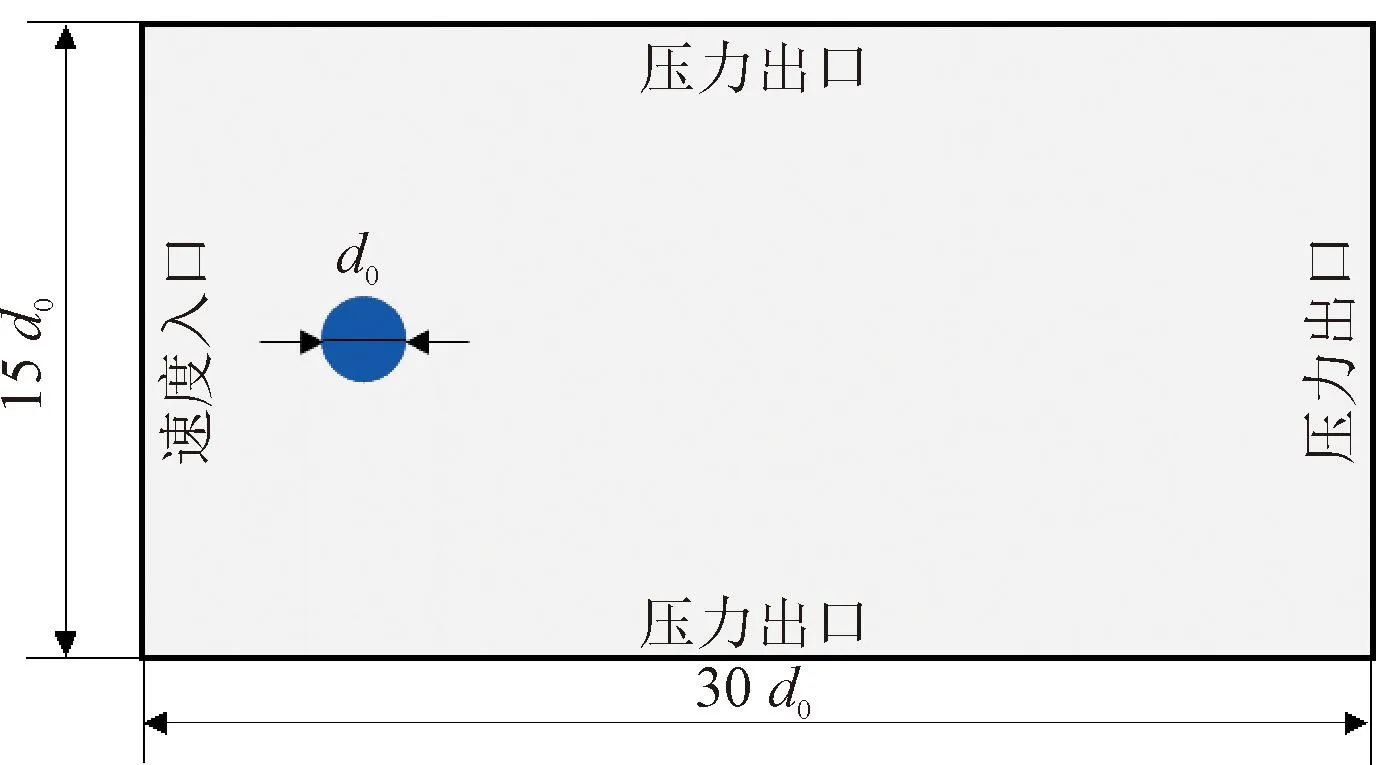
圖1 液滴破碎仿真模型Fig.1 Droplet breakup simulation model

1.2 CLSVOF相界面追蹤方法

液滴在氣流中的演化是一個復雜的兩相流過程,數值模擬的關鍵問題是如何有效地追蹤氣液相界面,目前常用的方法包括流體體積函數(volume of fluid,VOF)方法[19-20]、水平集(level set,LS)方法[22-23]以及CLSVOF方法[24-25]等。CLSVOF方法同時引入VOF相函數α和LS距離函數φ,結合2種方法的優點,采用分段線性界面重構思想,每次計算時需要對氣液兩相流界面重新構造,并對φ重新初始化。在CLSVOF方法中,氣液兩相流界面的追蹤是通過求解對流輸運方程實現的。方程的表達式可寫為

(4)

(5)

式中:t表示時間;v表示速度矢量;相函數α表示液相體積占單元體積的比值;距離函數φ表示單元中心到相界面的最小距離。

界面法向量n和界面曲率κ分別由LS距離函數φ計算得到

(6)

(7)

重新對相函數φ進行初始化,定義Sφ為單元中心到相界面的最小距離,正負由VOF相函數α確定,公式表達如下

(8)

1.3 網格無關性驗證

圖2給出了d0=0.1 mm、U0=15 m·s-1、We=12的工況下,基于不同網格得到的液氮液滴變形系數與時間的關系,其中h表示計算域的最小網格尺寸。由圖可見,當d0/h大于100時,液滴的變形系數隨時間的變化基本與網格尺寸無關,因此,在滿足計算精度的前提下,選取d0/h=100的網格最為合適。

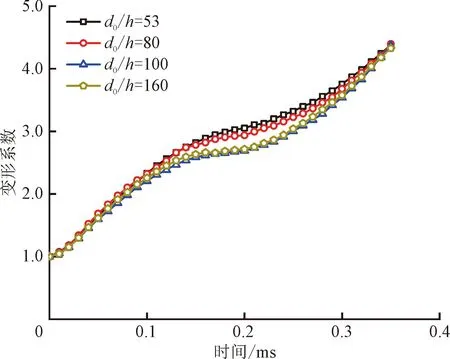
圖2 不同網格數量下液氮液滴變形系數與時間的關系Fig.2 The relationship between the deformation coefficient and the time under different grids

1.4 模型驗證

為了驗證模型的準確性,選取d0=0.78 mm、U0=50.4 m·s-1、We=33的水滴進行計算,將得到的水滴形態與文獻[17]中水滴的實驗結果進行對比,如圖3所示。由圖可見,在液滴中心凸起的周圍出現袋狀結構,其出現和破碎的時間基本一致,且母體液滴破碎后的子液滴分布規律相似,初步驗證了模型的可靠性。如圖4所示,選取d0=2.3 mm、U0=10 m·s-1、We=15的乙醇液滴,將本文模型計算得到的變形系數與文獻[26]的實驗結果進行對比,可以看出模擬結果與實驗結果一致性較好,統計后得到變形系數的最大偏差不超過10%,進一步驗證了模型的準確性。

圖3 水滴形態的模擬結果與實驗結果[17]的對比 Fig.3 Morphological comparison of simulation results and experimental results[17] of the water droplet

圖4 乙醇液滴變形系數的模擬結果與實驗結果[26]的對比 Fig.4 Comparison of simulation results experimental results[26]and on the deformation coefficient of the ethanol droplet

2 結果與分析

2.1 液氮液滴與常溫液滴對比

氣流中的液滴破碎特性與工質密切相關[27],表1展示了不同工質的物性參數。為探究低溫液氮液滴與常溫液滴的破碎特性差異,選取相同的初始直徑和氣流初始速度,對比了水滴、乙醇液滴和液氮液滴的形態演變規律,如圖5所示。

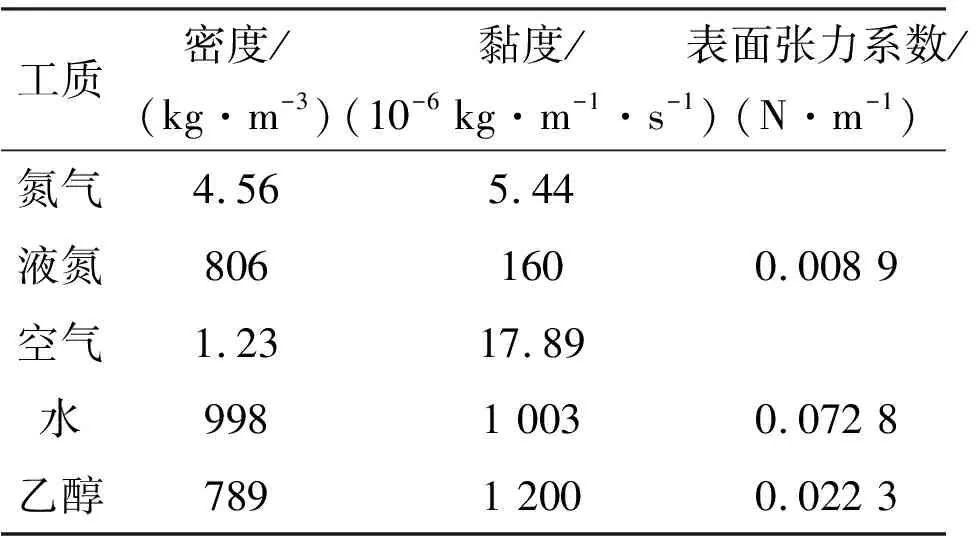
表1 工質物性參數(壓力0.1 MPa,液氮77.4 K,水和乙醇293 K)

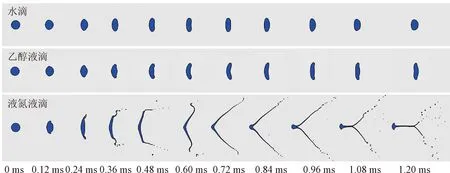
圖5 不同工質液滴形態的對比(d0=0.5 mm、U0=25 m·s-1)Fig.5 Morphological comparison of different droplets(d0=0.5 mm,U0=25 m·s-1)

由圖5可見,當水滴和乙醇液滴發生振蕩變形時,液氮液滴發生劇烈破碎,大量液滴顆粒從邊緣脫落。圖6給出了不同液滴的變形系數與時間的變化關系,可以看到在氣動力的作用下,水滴和乙醇液滴在垂直氣流方向被拉伸,變形系數增大,隨后在表面張力的作用下出現了回縮,變形系數減小;而液氮液滴的邊緣液滴顆粒則是快速脫落,液滴邊拉伸邊破碎,變形系數動蕩變化。液氮液滴與水滴和乙醇液滴的形態演變規律呈現明顯不同, 主要與液滴受到的氣動力和表面張力有關,氣動力促進液滴的變形和破碎,而表面張力抑制液滴的變形和破碎。在同一液滴初始直徑和氣流初始速度的工況下,低溫氮氣的密度高于常溫空氣,使得液氮液滴受到的氣動力更強。與此同時,液氮液滴的表面張力系數低于常溫液滴,其自身的表面張力更弱,因此,對于表征氣動力與表面張力相對大小的We而言,液氮液滴的We遠大于常溫液滴,更容易發生變形和破碎。

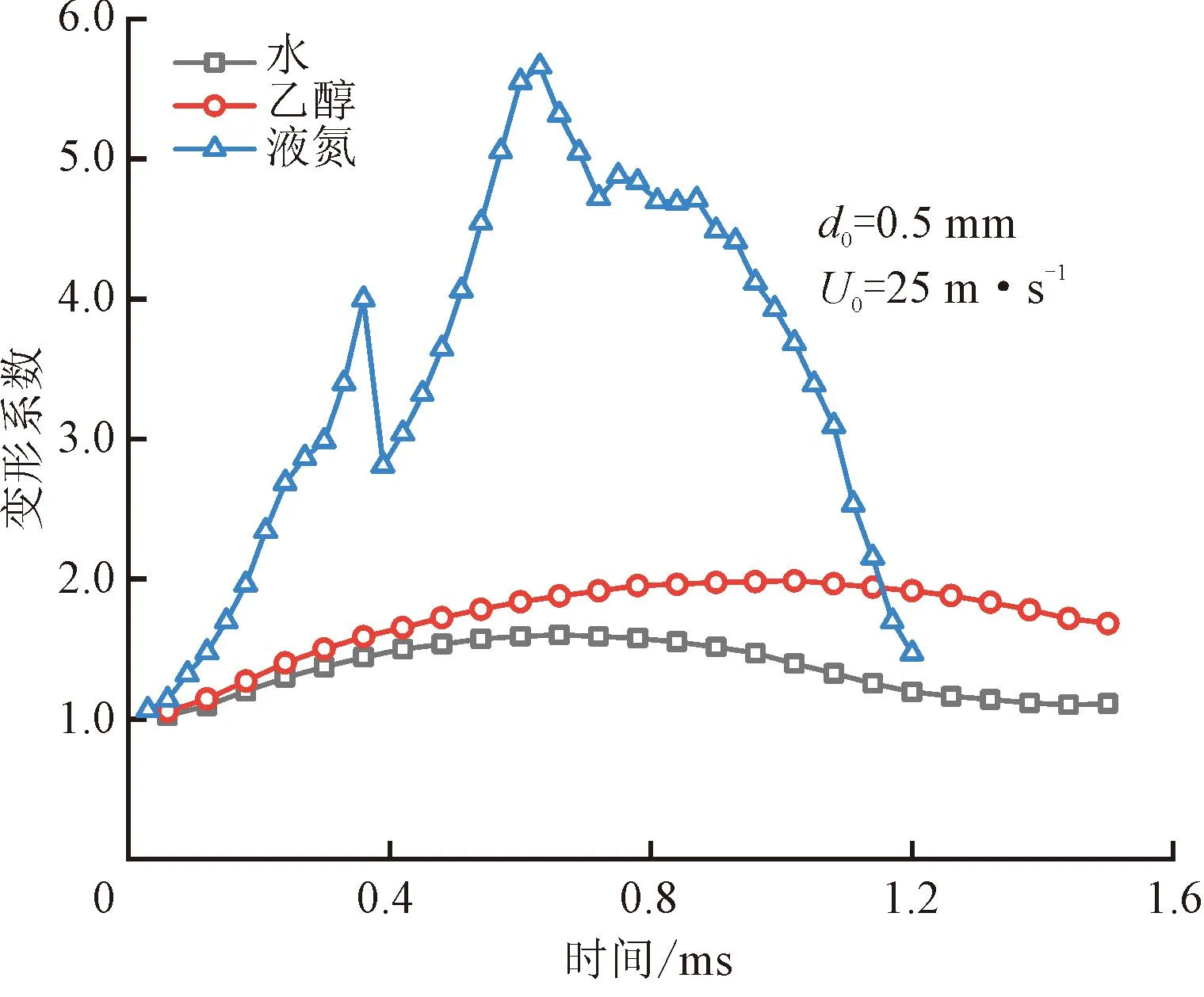
圖6 不同工質液滴變形系數與時間的關系Fig.6 The relationship between the deformation coefficient and the time under different droplets

2.2 破碎模式

圖7展示了不同破碎模式下液氮液滴的形態變化。由圖可見,低溫液氮液滴的破碎模式主要有3種,液滴在中心處出現袋狀結構,則在中心最薄處發生袋狀破碎;液滴在中心凸起的周圍出現袋狀結構,則在此最薄處發生多模式破碎;液滴未出現袋狀結構,則在液滴邊緣處發生剪切破碎。

計算所采用液氮液滴的最大Oh約為0.006,其黏性力的影響相較于表面張力可以忽略不計,則液滴破碎模式主要受We的影響[8],如圖8所示。隨著We的增大,液氮液滴依次出現袋狀破碎、多模式破碎和剪切破碎。

(a)袋狀破碎(We=12)

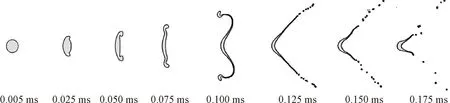
(b)多模式破碎(We=46)

(c)剪切破碎(We=128)

圖8 液氮液滴破碎模式與We的關系Fig.8 The relationship between breakup modes of liquid nitrogen droplets and We

圖9給出了不同破碎模式下的液滴壓力分布云圖。可見,當初始靜止的液滴位于低溫氣流時,首先在液滴中心出現高壓區,液滴邊緣出現低壓區,液滴在垂直氣流方向被拉伸,在沿氣流方向被壓縮。隨著時間增加,液滴低壓區范圍逐漸擴大,并出現氣體回流現象。在液滴迎風面和背風面的壓差作用下,球狀液滴向圓盤狀液滴過渡。當液滴發生袋狀破碎時,如圖9(a)所示,圓盤狀液滴(t=0.150 ms)在氣流方向上內凹,袋狀結構開始形成,此時液滴迎風面和背風面的壓差減小,袋狀結構不斷擴展,直至在液滴中心最薄處發生破碎。當液滴發生多模式破碎時,如圖9(b)所示,隨著We的增大,作用到液滴上的相對氣動力增大,垂直氣流方向上的液滴邊緣聚集了更多的液體,液滴變成不規則圓盤狀,導致液滴中心區域出現凸起,阻礙中心區域沿氣流方向的發展,袋狀結構開始出現在中心凸起的周圍(t=0.075 ms)。隨著袋狀結構的擴展,液滴在袋狀結構最薄處發生破碎,大量液滴顆粒從母體液滴脫落,母體液滴逐漸減小。當液滴發生剪切破碎時,如圖9(c)所示,作用到液滴上的相對氣動力進一步增大,在氣流剪切作用下,液滴顆粒開始從液滴邊緣脫落(t=0.036 ms),隨后液滴迎風面和背風面的壓差減小,處于邊拉伸邊破碎的狀態。相較于袋狀破碎和多模式破碎,發生剪切破碎的子液滴尺寸更小、數量更多。

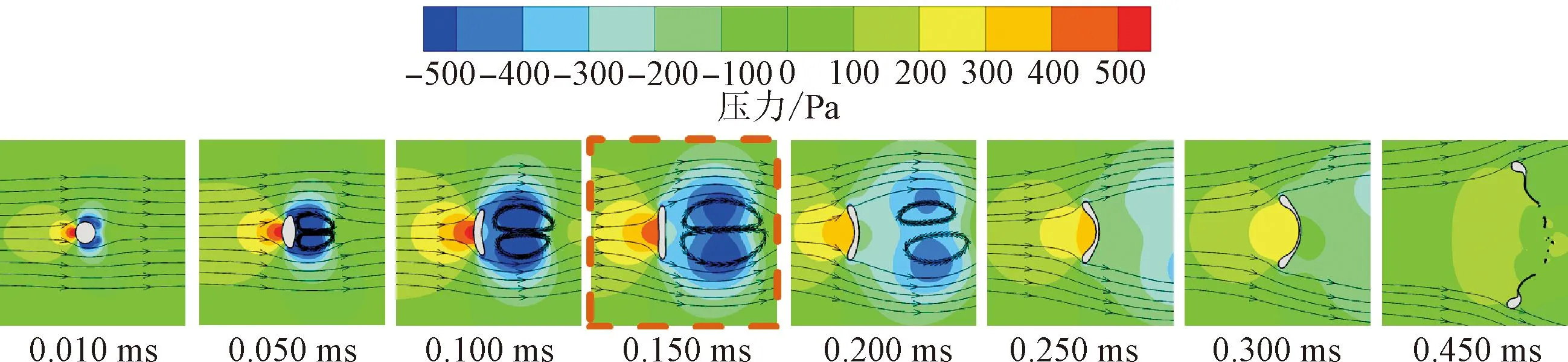
(a)袋狀破碎(We=12)

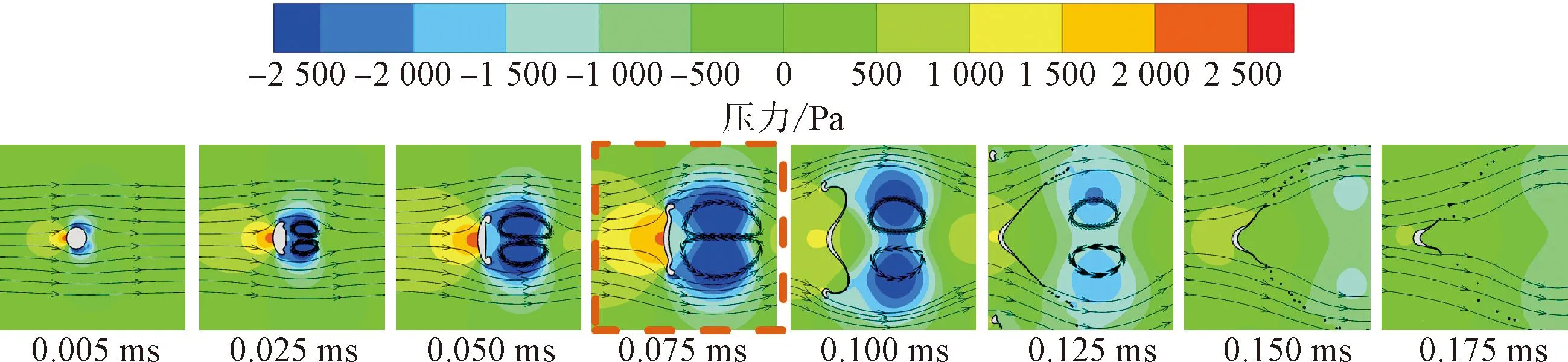
(b)多模式破碎(We=46)

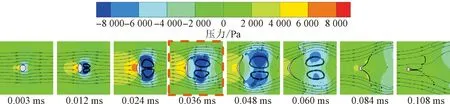
(c)剪切破碎(We=128)

在3種破碎模式下,低溫液氮液滴迎風面和背風面的壓差均隨時間呈現出先增大后減小的變化規律。如圖9中紅色框所示。對于袋狀破碎和多模式破碎,發生轉變的原因是袋狀結構開始形成;而對于剪切破碎,發生轉變的原因是邊緣液滴顆粒開始脫落。

2.3 變形系數

不同We下液氮液滴的變形系數與無量綱時間的關系如圖10所示,可以看到,在不同的We下,由于液氮液滴的破碎模式不同,液滴變形系數的變化規律差異明顯。當We=12時,液滴發生袋狀破碎,液滴在初始階段由球狀變為圓盤狀,變形系數快速增大;袋狀結構開始產生后,變形系數增速減緩;隨著袋狀結構進一步擴展,變形系數增速加快。當We=35時,液滴發生多模式破碎,液滴變形系數快速增大直達峰值,此時液滴在中心凸起周圍的袋狀結構最薄處破碎,變形系數驟降。當We分別為58、81、104時,液滴發生剪切破碎,液滴在初始階段的變形系數增速更大,當液滴開始發生破碎時,邊緣處的液滴顆粒脫離,母體液滴減小,液滴處于邊拉伸邊破碎的狀態,直至母體液滴不再破碎為止。

圖10 液氮液滴變形系數與無量綱時間的關系Fig.10 The relationship between the deformation coefficient of liquid nitrogen droplets and dimensionless time

2.4 時間特性

圖11展示了不同初始直徑下,液氮液滴的無量綱初始破碎時間與We的關系,并將本文計算結果與Hsiang和Faeth[8]、Pilch和Erdman[10]的實驗擬合曲線進行對比。由圖11可見,隨著We的增大,液氮液滴的無量綱初始破碎時間整體呈現減小趨勢,這是由于隨著We的增大,液氮液滴所受到的氣動力相較于液滴的表面張力增大,液滴更容易克服表面張力的阻礙作用而產生袋狀結構或邊緣液滴顆粒脫落,導致液滴的無量綱初始破碎時間減小。不同We下的無量綱初始破碎時間均包含在Hsiang和Faeth[8]、Pilch和Erdman[10]的實驗擬合曲線范圍內,且無量綱初始破碎時間隨We的變化趨勢與Pilch和Erdman[10]的實驗結果規律相一致。

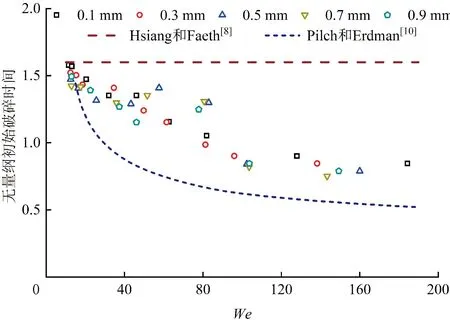
圖11 無量綱初始破碎時間與We的關系Fig.11 The relationship between dimensionless initial breakup time and We

臨界變形系數定義為初始破碎時間的液滴變形系數,也是表征液滴破碎特性的重要參數之一。圖12給出了不同初始直徑下,液氮液滴的臨界變形系數與We的關系,并將本文模擬結果與Hsiang和Faeth[8]、Dai和Faeth[12]的實驗擬合曲線進行對比。

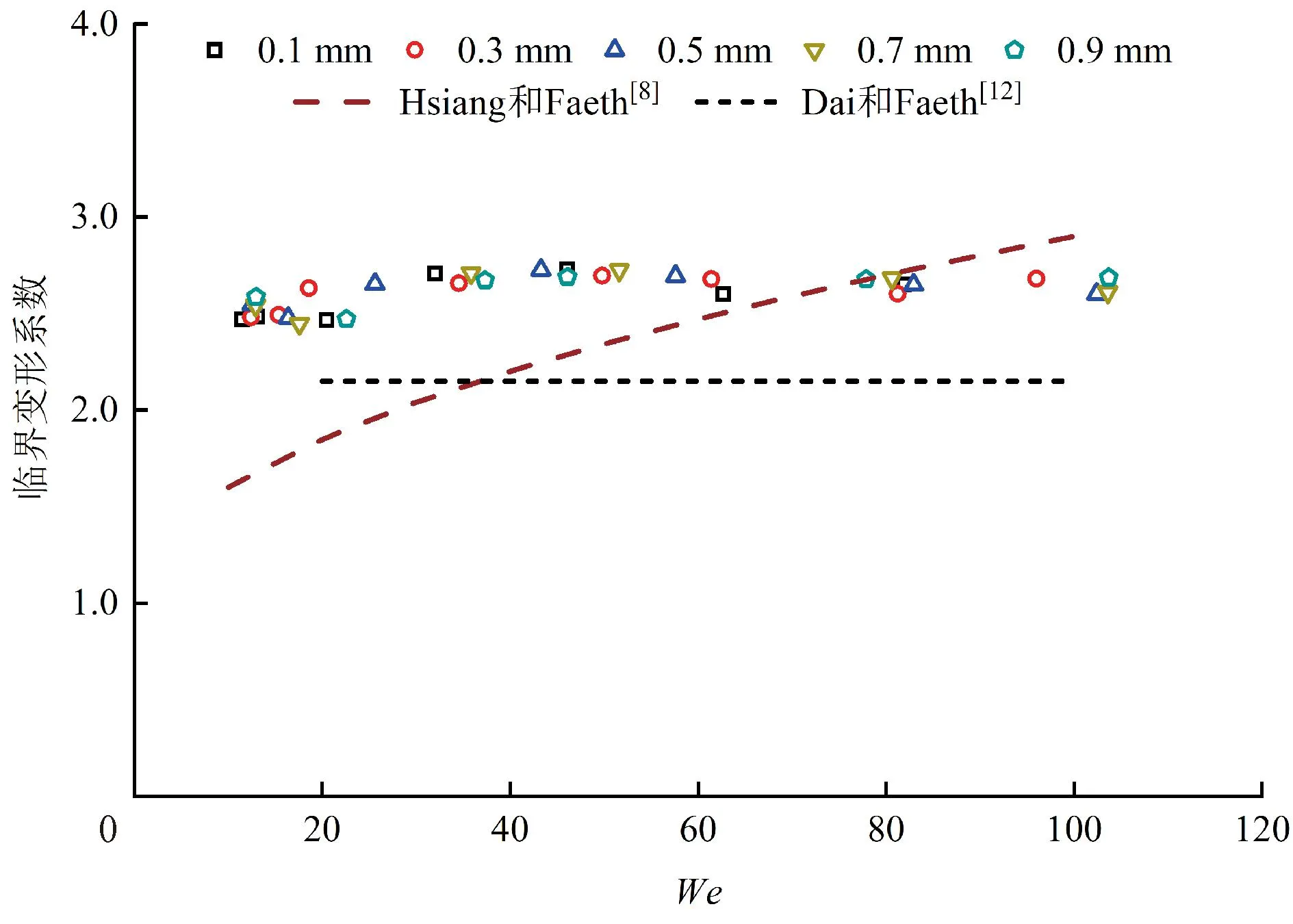
圖12 臨界變形系數與We的關系 Fig.12 The relationship between critical deformation coefficient and We

由圖12可知,對于不同初始直徑的液氮液滴,在0

3 結 論

基于CLSVOF方法,采用自適應局部網格加密技術,構建了低溫風洞中的液氮液滴破碎模型,探究了低溫風洞中液氮液滴的破碎特性,得到如下結論。

(1)液氮液滴與常溫液滴具有不同的形態演變規律,在同一液滴初始直徑和氣流初始速度的工況下,常溫液滴發生振蕩變形,液氮液滴發生破碎。

(2)液氮液滴破碎模式主要由We決定,隨著We的增大,低溫液氮液滴依次發生袋狀破碎、多模式破碎和剪切破碎。

(3)在不同的破碎模式下,液氮液滴迎風面和背風面的壓差均隨時間呈現出先增大后減小的規律,且發生轉變的原因與破碎模式有關。對于袋狀破碎和多模式破碎,發生轉變的原因是袋狀結構形成;而對于剪切破碎,發生轉變的原因則是邊緣液滴顆粒脫落。

(4)在不同的We下,液氮液滴呈現不同的破碎模式,變形系數的變化規律差異明顯。

(5)隨著We的增大,作用到液氮液滴上的相對氣動力增大,液氮液滴無量綱初始破碎時間減小。在0