基于降階模型的熱過程快速預測方法研究

張光鵬,張 珺,李文超,齊 健

(1.中北大學 航空宇航學院,山西 太原 030051;2.太原學院 數學系,山西 太原 030001)

熱過程控制是工業生產的重要組成部分,被廣泛應用于熱處理和催化裂解等生產工序中,對產品質量、生產效率和收益等有重大的影響,因此對熱過程控制進行分析、設計和優化有著重要的意義[1-2]。

目前,熱過程控制系統響應一般通過計算流體力學(CFD)的方法進行熱流耦合數值模擬。陳文杰[3]等采用CFD方法模擬了出口壓力、壁面溫度及轉速等參數對柱塞油膜摩擦生熱引起溫度變化的影響規律,發現出口壓力對油膜摩擦生熱引起的溫升影響較小,壁面溫度每上升 20 K,油膜溫度上升量近似降低50%。邱彤[4]等CFD方法對爐膛內流動、燃燒、傳熱和傳質過程進行了研究,發現可以通過增加側壁燒嘴來彌補爐膛頂部熱量的不足的問題。熊天軍[5]等采用CFD方法對嚴寒地區某工業廠房冬季不同的供暖末端進行了研究,發現熱風機難以將暖空氣送至人員工作區域,并且會導致較大的垂直溫度梯度與室內溫度分布不均,從而增大所需供熱量,而采用輻射地板可以以最少的熱量供應達到相同的平均操作溫度。陳思[6]采用CFD方法研究了蓄熱材料充填蓄熱室熱過程,討論了其吸熱和放熱過程的影響因素,實現了蓄熱室熱過程兩相對流、傳導、輻射的非穩態耦合計算。傳統熱過程控制采用CFD方法估計系統的響應,雖然可以估計熱過程控制系統的溫度分布特征和溫度-時間響應,能夠滿足熱過程控制設計的需要,但該方法計算量大耗時長、無法實時調整系統的控制率,導致對熱過程系統控制率的優化周期較長、成本較高,尤其難以實現熱過程控制的“實時”優化。

降階模型大致可分為兩種:一種基于流場特征模態(如POD、子空間投影等),另一種基于系統辨識和數據驅動(如Volterra級數、神經網絡等),前者建模需要全流場信息,而后者則只需要少量的輸入輸出樣本,以簡潔的數學表達式描述全階非定常流動系統[7]。因此,后者更適用于熱過程控制系統的動態響應問題。Volterra級數是一種范函級數,描述了非線性時系統的輸入輸出關系,可以任意精度逼近連續函數。Volterra級數降階模型根據已知的試驗數據或仿真數據,辨識系統輸入和輸出之間的關系,是一種能夠體現系統非線性特征的簡單數學模型,其精度與CFD接近且計算效率遠高于CFD,為非線性系統響應的快速估計提供了有力的方法和工具[8]。本文采用高效精確的Volterra級數降階模型方法替代CFD方法,提高熱過程控制系統的溫度響應預測效率,為熱過程系統的控制和優化提供了新的方法。通過一個系統溫度控制的算例,研究了降階模型辨識方法替代CFD方法的可行性,討論了基于降階模型優化熱過程系統控制率的可行性。

1 基于Volterra級數的熱過程響應的降階模型分析方法

在某些工業生產過程(如熱處理、催化裂解等)中需要對加熱過程進行嚴格控制,使被控對象的溫度按一定規律進行變化或基本恒定在某一數值上。對于這類熱過程控制系統,其輸出變量為系統溫度,輸入變量可以是加熱溫度、加熱氣體泵送壓力、加熱氣體流量、加熱棒的功率等[9],為簡化問題,本文以加熱溫度為控制輸入變量展開討論,對于其他控制變量也可以采用同樣的方法進行研究。

溫控系統的輸入溫度T和輸出溫度Y之間的關系可表示為

{Y(t)}=Ψ{T(t)}

(1)

式中:t為時間,s。

以上關系涉及流體力學和傳熱學等多個學科,是一個非線性的函數,常采用CFD方法求解,考慮到CFD方法的缺點,本文采用非線性降階模型的方法研究上述溫控系統,選擇基于Volterra級數的降階模型來實現溫控系統的熱過程快速預測和優化。

對于公式(1)表示的溫控系統,其離散格式Volterra級數降階模型可寫為[10]

(2)

式中:T(n)為離散的系統溫度輸入向量;Y(n)為離散的系統溫度輸出向量;n=0,1,…為離散時間,s;H0為系統穩態溫度,K;H1為溫度響應的一階核函數矩陣;H2為溫度響應的二階核函數矩陣。

通過已有的系統的輸入輸出關系,辨識公式(2)中的H0、H1、H2,可得離散格式的系統響應降階模型。用該降階模型,可以計算任意輸入下系統的響應[11-12]。基于Volterra 級數的降階模型的關鍵在于核函數的辨識,核函數可由脈沖信號法、階躍信號法或者隨機信號下的響應來識別。由于Volterra 級數降階模型二階及以上的核函數數量大,識別核函數困難,因此一般采用一階Volterra 級數降階模型[13-16]。將式(1)所表示的溫控系統按照一階離散格式的Volterra級數展開,可以得到該系統熱過程響應的降階模型:

(3)

在建立上述降階模型后,可以進一步進行系統熱過程的快速預測和優化。溫控系統降階模型建立、熱過程快速預測和控制率優化的具體步驟如下:

(1)建立溫控系統的CFD模型;

(2)在CFD模型上施加階躍溫度輸入信號,得到溫控系統的溫度響應;

(3)通過溫控系統的輸入溫度和響應溫度,辨識公式(3)中的核函數;

(4)將核函數代入式(3),構造溫控系統的降階模型;

(5)改變輸入溫度的時間變化規律,采用降階模型得到對應的系統溫度時間變化規律;

(6)重復步驟(5)得到最優的溫度控制率。

2 熱過程控制系統算例說明

某溫度控制系統如圖1所示。該系統為球體,球體直徑44 m,加熱氣體入口直徑0.5 m,減壓排氣口直徑0.5 m,入口和出口夾角為90°。通過空氣進行加熱,系統的輸入變量為入口加熱氣體的溫度,輸出變量為該系統的壁面溫度。對壁面的溫度進行控制,要求在最短時間內將壁面溫度從300 K均勻加熱至550 K左右,壁面最大溫差不超過50 ℃。

圖1 溫控對象模型

3 熱過程控制系統算例響應降階模型

采用CFD獲得階躍溫度下熱過程控制系統的響應。CFD計算時流體為空氣,k-e湍流模型,球體內部的初始溫度為300 K,出口為大氣,入口加熱氣體流速8 m/s。入口加熱氣體的溫度為控制變量,計算時采用階躍溫度,階躍幅值為300 K,入口溫度如圖2(a)所示,在階躍輸入溫度下計算得到的系統壁面最高溫度、平均溫度和最低溫度如圖2(b)所示,系統壁面溫差如圖2(c)所示。不同時刻球體內部溫度分布如圖3所示。

圖2 球體入口溫度及其響應

圖3 CFD計算得的系統溫度

根據圖2辨識系統壁面溫度變化的核函數,結果如圖4所示。將核函數代入式(3),得到該系統壁面溫度響應的降階模型。為驗證降階模型方法的可行性和該降階模型精度,分別用降階模型和CFD計算了任意入口控制溫度下系統的響應,兩者的結果如圖5所示。從圖5可以看出,降階模型方法得到的升溫曲線與CFD方法得到的升溫曲線重合,這說明了基于Volterra級數的降階模型方法是可行的,所建立的降階模型是精確的,能夠用來正確估計該系統輸出溫度隨控制溫度的變化規律。

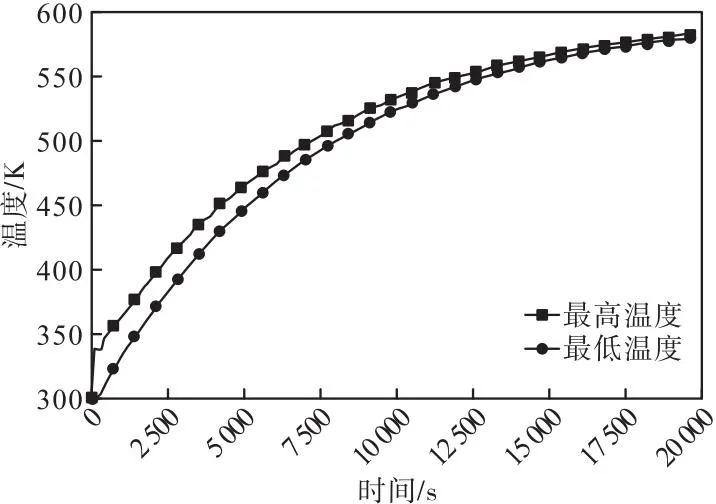
圖4 溫度變化的核函數

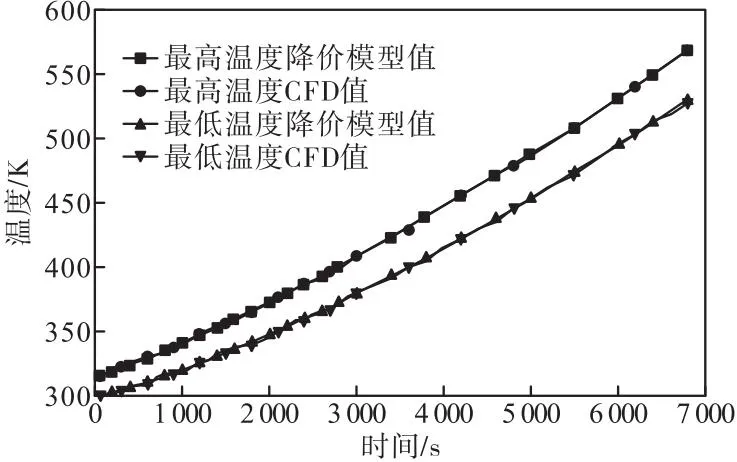
圖5 升溫曲線對比結果

4 熱過程控制系統算例控制率的優化

為了優化圖1所示熱過程控制系統的熱控制過程,將降階模型代入優化算法,用于預測任意控制溫度下溫控對象壁面溫度的響應,通過優化算法調整溫度控制率實現熱過程的優化。根據算例的要求,入口溫度控制率采用線性函數T=at+T0,該函數有兩個控制變量:起始控制溫度T0和升溫斜率a。經過優化,發現當入口加熱溫度T與時間t的關系滿足T=0.06t+450 K時滿足設計要求,這時的輸入溫度波形如圖6(a)所示。用CFD計算了優化方案的系統響應,發現CFD結果與降階模型結果一致,優化后系統壁面的升溫速率基本保持不變,且耗時更短,對比如圖6(b)所示。系統的溫差變化如圖6(c)所示,升溫過程中最大溫差為38 ℃,溫差滿足設計要求。

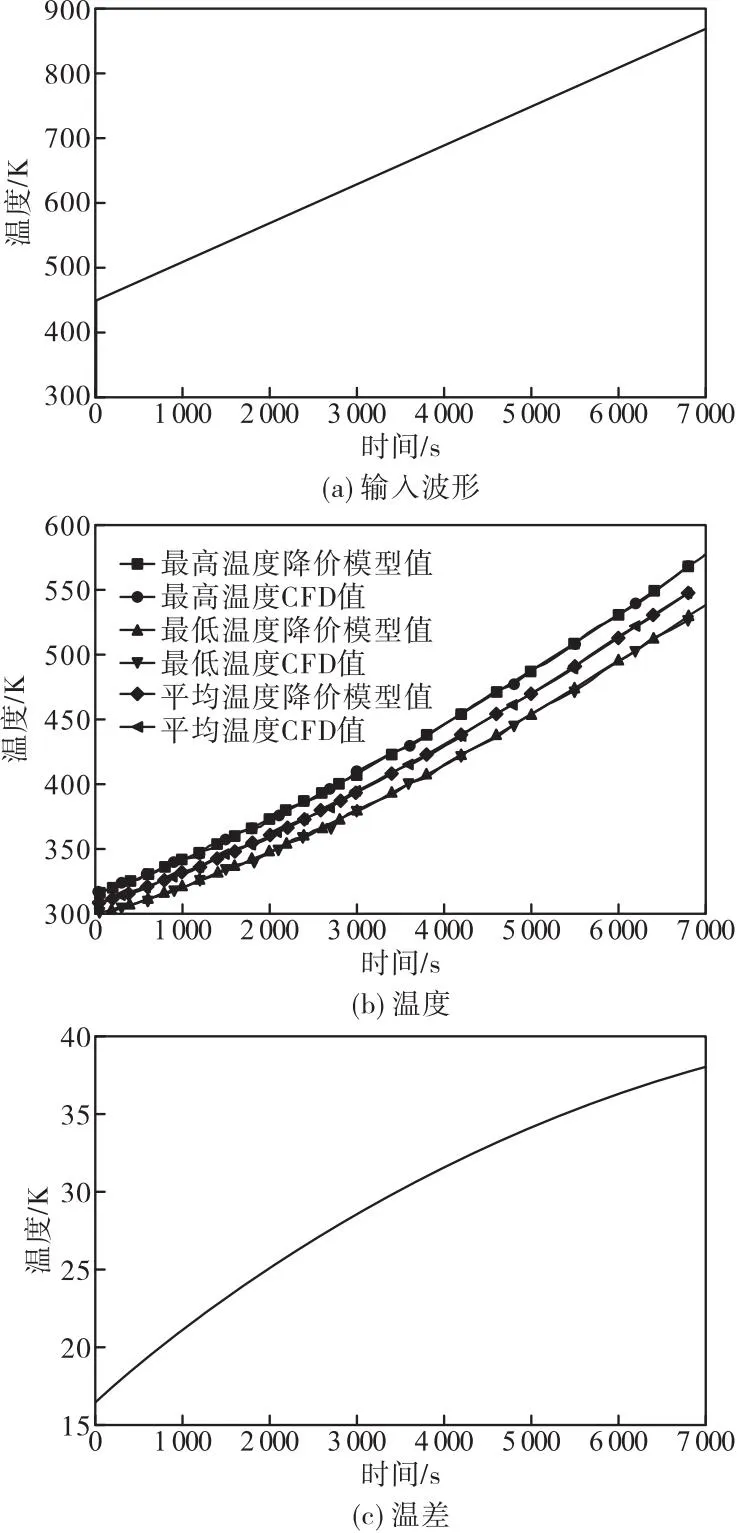
圖6 系統升溫優化結果

需要說明的是,上述溫度控制系統算例的CFD網格數量約15萬,在96線程Xeon PLATINUM 8175M并行計算機上進行一次模擬需要6 h,優化迭代20次共計120 h。而采用降階模型方法進行優化僅需要1 s,加上采用CFD進行階躍響應分析的時間,總耗時6 h,效率提升顯著,而且該降階模型可以用于實時控制過程。

5 總 結

本文提出了一種基于一階Volterra 級數的降階模型的熱過程快速分析預測方法。該方法根據階躍加熱下系統的響應,構建系統溫度與控制條件之間關系的降階模型,并用該降階模型快速預測和優化不同控制條件下系統的響應,為熱過程控制策略制定及控制參數確定提供了一種工具。算例的結果表明:利用降階模型方法得到的結果與CFD的結果一致且效率提升顯著,可以快速得到不同溫度輸入波形下溫控系統的響應,且不需要反復進行CFD計算,證明了基于Volterra 級數的降階模型方法在熱過程快速預測和優化研究中的可行性和高效性。