高三數學復習課的教學反思
黃 飛
? 江蘇省海門中學
在高三復習課教學中,高效率、高質量是復習課教學追求的根本目標,這就要求教學應從多個層面入手,教師角色、學生角色以及復習內容、配套練習等多個方面都要進行考慮,從而在有限的時間和空間內采取恰當的教學方式,設置合理的課堂容量等,全面提升課堂的“高效”與有效性.
高三數學復習課教學,課堂上知識點的容量、題型的分類、學情的把握等都需要教師認真去思考,并在備課與教學中做到有的放矢.
1 容量要適中
高三數學復習課教學中,課堂容量要適中,要保證基礎薄弱的學生能鞏固基礎的知識點和公式計算,也就是基本知識和基本能力的培養;對于中等水平的學生,能聽懂更多內容,能理解公式的內涵,會對公式進行變形計算,會進行知識遷移,會做更多同類型的題目,培養發現問題與解決問題的能力;對于學習優秀或者是能自學一部分知識的學生,綜合性的題目要有所涉及,讓這部分學生能吃飽,有所學.
例如,在解析幾何模塊的復習教學中,要充分結合解析幾何知識點多,曲線類型多,點、線、角、曲線多元素并存等特點,以及解題過程相對比較繁雜、運算量大、對能力要求高、交匯性與綜合性強等基本特點,合理從“設”入手,通過“設點”或“設線”視角切入,優化解題過程,提升解題效益.
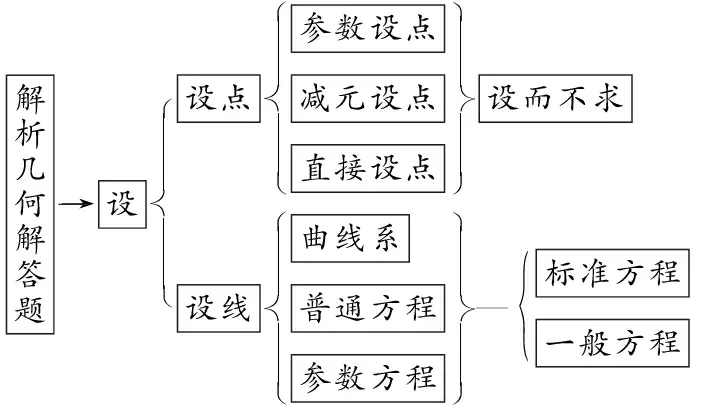
圖1
合理設置題型與題量,如圖1所示,在遵循“設—列—解”基本解題程序的步驟與基礎上,重點突出解析幾何“設”的技巧性與重要性,強化數學思想方法,減少數學運算,優化解題過程,從而實現該模塊知識的復習教學.
具體教學過程中,可以選取典型例題,以“設點”與“設線”等不同視角切入,合理結合“一題多解”,巧妙融入解題技巧與策略,實現復習教學的基本目標.
適中的復習教學容量,以符合大部分學生的需求,才能真正面向大部分學生,使復習的受益面盡可能大.
2 分類要合理
著名數學家華羅庚說:“人們早就對數學產生了枯燥乏味、神秘難懂的印象.成因之一便是脫離實際.”因而,在實際教學與復習中,要將數學知識與數學應用加以交匯,通過合理的分類與設計,以激起學生學習數學的欲望.
具體復習教學中,典型例題的分類也要合理,從基礎題型到綜合題型,要有梯度,由易到難,循序漸進,學生的學習應遵循這個規律,否則知識就會夾生,學生感覺學到了一點,可還是有一些不明白的地方.
例1[2024屆江蘇省淮安市高三(上)期末數學試卷](多選題)已知函數f(x)滿足?x1,x2∈R,都有|f(x1)+f(x2)|≤|sinx1+sinx2|成立,則下列結論正確的是( ).
A.f(0)=0
B.f(x)是偶函數
C.f(x)是周期函數
D.g(x)=f(x)-sinx,若-1 分析:根據題設條件,通過合理的賦值處理,結合各選項中信息加以剖析與確定. 解法1:(嚴謹推理法)依題意?x1,x2∈R,都有|f(x1)+f(x2)|≤|sinx1+sinx2|成立. 令x1=x2=0,可得|f(0)|≤0,則f(0)=0,故選項A正確. 令x1=-x2=x,可得|f(x)+f(-x)|≤|sinx+sin (-x)|=0,則f(x)+f(-x)=0,即f(-x)=-f(-x),可知f(x)是奇函數,故選項B錯誤. 令x1=-x,x2=x+2π,得|f(-x)+f(x+2π)|≤|sin (-x)+sin (x+2π)|=0,則f(-x)+f(x+2π)=0,即f(x+2π)=-f(-x)=f(x),可知f(x)是周期為2π的周期函數,故選項C正確. 而由sinx1-sinx2≤f(x1)-f(x2),可得f(x2)-sinx2≤f(x1)-sinx1,又g(x)=f(x)-sinx,則有g(x2)≤g(x1),故選項D正確. 綜上分析,正確的選項為ACD.故選擇:ACD. 解法2:(特殊函數法)取函數f(x)=sinx,滿足?x1,x2∈R,都有|f(x1)+f(x2)|≤|sinx1+sinx2|成立,易知正確的選項為ACD. 熟練掌握一些具有特定結構特征的基本初等函數類型(如冪函數、指數函數、對數函數以及三角函數等),以及與函數相關的基本性質等,結合問題實際,借助“模特”函數的構造,化抽象為具體,可以為解決此類問題的特殊函數模型思維與構建提供理論依據,也是綜合創新應用的理論基礎. 高三數學的復習課教學要合理分類,對章節知識、具體知識點、某一思想方法、技巧策略等方面加以針對性復習,根據不同復習階段以及不同復習內容合理設置,有效提升復習效益. 美國教育心理學家奧蘇貝爾曾說:“影響學習的最主要原因是學生已經知道了什么,我們應當根據學生原有的知識狀況去進行教學.” 在實際復習課教學中,教師不能盲目地以自身的理解去安排復習,而要綜合具體班級學生的學情,教學設計要契合學生的需求.而對學情的把握,教師需要多和學生溝通,了解學生有什么困難,有什么收獲等. 該題中的函數是以含有根式的代數式形式呈現的.此代數式是一個一次式與一個根式的和,二者之間不對稱,形成“階數”差,這也是此類函數解析式的結構特征. 在例2的基礎上,根據學情予以變式與拓展. (1)同類變式 保留函數解析式的“階數”差的結構特征,從不對稱中尋找解題視角,以相似的視角來加以變式與應用. 解析:提示函數f(x)在(-∞,1]上單調遞增,其最小值為2. (2)異類變式 改變函數解析式的“階數”差的結構特征,兩個代數式均由根式組成,從對稱中尋找解題視角,以相異的視角來加以變式與應用. 解析:方法1:三角換元法. 函數f(x)的定義域為{x|0≤x≤1}. 方法2:基本不等式法. 函數f(x)的定義域為{x|0≤x≤1}. 又[f(x)]2≥1,所以1≤[f(x)]2≤2. (3)升類變式 提升函數解析式的復雜程度,由兩個根式的線性運算升級為三個根式,拓展數學思維,提升解題技巧與能力,從而加以升級變式與應用. 解析:依題知函數f(x)的定義域為{x|-1≤x≤1}. 在實際的高三數學的復習課教學中,教師正確并合理把握學情,讓學生積極主動參與其中,借助典型例題的引導,去經歷、去體驗、去反思、去提升,從而不斷構建更加全面的知識網絡體系,展示學生自身的個性特征與獨立思考的習慣,參與到學習的過程中去,使得學生的情感態度以及學習能力等各方面都能得到培養和發展. 高三數學的教學,要借助配套練習加以反饋與提升.特別是在學生練習后,注重信息收集與反饋,根據學生對復習內容的理解與掌握層次等,合理糾正與改進,同時對后繼復習作出合理調整,以提升復習教學的質量與效益. 總之,高三數學的復習課教學中,要根據本班實際,充分把握學情,確定并明確復習教學目標,通過適中的教學容量,以及數學知識的合理分類,結合巧妙的教學方式與合理安排,激發學生的學習興趣,促使學生自主復習與深入研究,借助有效練習,合理反饋信息,并在分析、練習、反饋、反思中總結,高效提升高三數學復習課的質量與效益.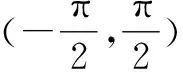
3 學情要把握
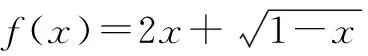
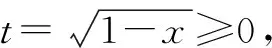
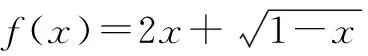

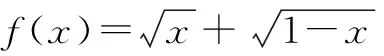
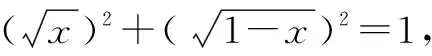
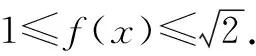
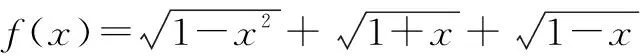
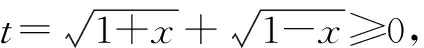
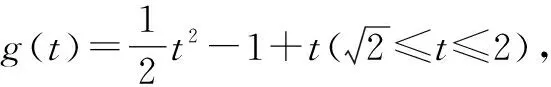
4 信息要反饋

