建構基于“三個理解”的高效復習課堂

李淑萍

? 山東省菏澤市第三中學

在高三數學教學中,復習課是一種常態課.那么,復習課需要完成哪些主要任務呢?通過復習,將以往所學的知識點進行全面系統梳理,從而形成系統的、穩定的認知結構;結合課程標準進行考點的梳理,做好查缺補漏;通過模塊化復習,挖掘出問題的本質,找到問題的一般規律;通過復習,抽象概括出重要的數學思想方法,從而更好地理解數學、應用數學,培養良好的思維品質[1].若想發揮復習課的價值,自然離不開教師的精心籌備,而受傳統教學理念的影響,大多教師在課堂上習慣于應用“師問生答”的方式將知識點進行羅列,雖然課堂上也有互動,但僅局限于問答,學生的學習是被動的,難以激發學習興趣.部分教師在組織教學時,習慣于按照教材的順序展開復習,未從整體和全局上進行建構,因而知識結構性不強,不利于知識的遷移.另外,在復習過程中,過多強調“刷題”卻不重視方法的提煉和總結,因此仍然會出現“懂而不會”的現象.當然,還有部分教師在復習課教學時,未能從學生的最近發展區出發把握學情,從而影響學生參與的積極性,不僅難以發揮學生的主體作用,而且因為內容不符合學生認知規律而導致參與率低下,課堂氛圍沉悶、消極.可見,要上好復習課就要避免簡單的內容羅列和盲目的“題海”,應從學生認知出發,找到合適的切入點,從而激發思維活力,促進解題效率提升.

筆者以“函數的單調性”為例,從“三個理解”出發,談了幾點對高三數學復習的粗淺認識,以拋磚引玉,啟發思考.

1 理解數學

理解數學,如果單純地靠理解知識去解決數學問題還不夠,還應清楚知識產生的背景、形成過程和形成方法;準確把握知識的本質、結構,挖掘出數學知識中蘊含的數學思想;還要明晰知識點之間的聯系,進而形成以核心知識點為節點的縱橫交錯的知識網絡[2].在學習數學時,只有知道知識從哪里來,能解決哪些問題,才能真正地理解數學并應用好數學;只有經歷知識產生、發展的過程,才能讓學生真正地理解知識,并將知識和方法轉化為學習能力,形成正確的數學觀.為此,教師要清楚知識的邏輯結構,這樣教學才能有條不紊地順利開展,才能讓學生抓住學習的重難點,從而進行科學的建構.

問題1我們在學習函數時,一般從哪幾方面來研究呢?

設計意圖：數學邏輯性強,在解決一個問題時往往會涉及其他問題,在教學過程中只有將知識放在一個系統中,才能使知識的學習更加自然,知識的應用更加流暢.為此,教師引導學生回憶學習函數的過程,將函數的單調性置于解決問題的系統中,從而豐富研究方法,拓寬研究途徑.

問題2與初中函數單調性相比,高中階段有哪些變化呢?(從數學表達角度進行分析.)

設計意圖：與初中知識相串聯,通過區別和聯系呈現函數單調性的發展過程,讓學生感受數學知識的學習一般需要經歷從直觀到抽象、從感性到理性的過程,從而在梯度變化中體驗數學學習的樂趣.與此同時,將函數的單調性從知識體系中提取出來,呈現本節課的研究重點,明確復習方向.

問題3說一說你是如何理解增函數的.

設計意圖：通過開放性的問題引導學生結合自己的認知進行多角度聯想,通過合作交流構建起完整的知識鏈.

問題4單調性證明.

例1已知函數f(x)的定義域為R.

(1)f(2)>f(1)是函數f(x)在R上為增函數的______條件;

(2)f(2)>f(1)是函數f(x)在(0,+∞)上不是單調減函數的______條件;

(3)f(x)在R上為單調增函數是其在(-∞,1)和(1,+∞)上都是單調增函數的______條件;

(4)函數y=f(x)是區間D上的單調函數,則直線x=a與函數f(x)圖象有______個交點.

設計意圖：借助實際應用強化對知識的理解,以此促進知識的內化,提升解題能力.如問題(1)引導學生從逆向理解,即若f(x)為增函數,f(x1)>f(x2)?x1>x2;問題(2)則從反面出發,讓學生深化理解減函數;問題(3)則利用反例法來分析,讓學生知曉若一個函數有多個單調區間時,不能直接用“∪”連接;問題(4)在理解單調區間與定義域關系的基礎上,培養學生數形結合意識.這樣在問題的引領下,將教材中關于判斷函數單調性的問題進行串聯,多角度呈現概念的重要價值,引導學生在解決問題時善于回歸概念,回歸問題的本源.

在復習階段切勿好高騖遠,要重視回歸課本,挖掘問題的本質,進而通過知識點的整合和重建實現認知結構的優化,讓學生有能力去解決更有挑戰性的問題,提升解題信心和解題能力.

2 理解學生

眾所周知,脫離學生實際的教學必然是低效的,為此,教師在開展教學活動時一定要理解學生.教師要清楚學生基礎知識的掌握情況,清楚學生的思維特點,清楚學生的困惑點和薄弱點,從而進行有針對性的查缺補漏,挖掘出新的生長點,促進學生學習能力的進一步提升.只有真正地理解學生,才能設計出符合學生最近發展區的問題,讓學生夠得著又能有所提高.同時,教學設計只有符合學生思維發展特點,符合學生心理需求,才能激發學生的學習興趣,引起師生情感的共鳴,從而讓學生積極主動地參與到教學實踐中去,使課堂呈現勃勃生機[3].

分析學生作業及課前測評時發現,學生在理解函數的單調性上還存在以下幾個問題:①判斷函數單調性時容易忽視定義域;②將函數單調性的判斷和證明混為一談;③對分段函數的單調性理解不夠充分;④在應用函數單調性解決問題時容易思維受阻.結合以上學情,教師在復習階段可借助練習幫助學生厘清問題的來龍去脈,從而達到深化理解,靈活應用的效果.

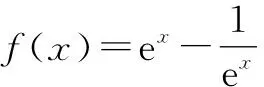
設計意圖：引導學生嘗試應用不同方法證明,進而總結歸納出證明函數單調性的一般方法,即定義法和導數法,結合學生呈現的問題進行詳細講評,從而構建證明函數單調性的方法系統.

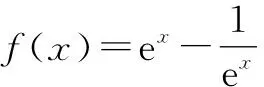
設計意圖：與例2形成對比,通過區別和聯系深化知識的理解,同時整理歸納出判斷函數單調性的方法,如定義法、圖象法、復合函數法和導數法等.

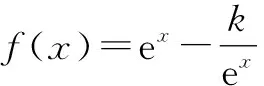
設計意圖：學生在遇到含參問題或反向推理問題時容易出現思維障礙,借助例4充分暴露學生思維過程,借助講評培養學生的轉化意識.如例4在求解時可將其轉化為求f′(x)≥0恒成立的問題,轉化后的問題更符合學生的認知,求解自然也就水到渠成了.

例5已知函數f(x)=ex-e2-x.

(1)若f(x1)>f(x2),求證:x1>x2;

(2)若f(x1)+f(x2)>0,證明:x1+x2>2.

設計意圖：本題是一個綜合性問題,主要考查學生對單調性本質的理解.對于問題(1),可以將其轉化為證明函數單調性的問題.對于問題(2),可以構造函數y=f(x+1)是奇函數且為增函數,由f[(x1-1)+1]+f[(x2-1)+1]>0,得出結論;也可以回歸概念,利用反證法證明,假設x1+x2≤2,因為x1≤2-x2,x2≤2-x1,結合函數為單調增函數,可得f(x1)+f(x2)<0,與已知f(x1)+f(x2)>0相矛盾,所以假設不成立,則x1+x2>2.

結合學情設計了針對性的練習,充分暴露學生在解決函數單調性問題時的障礙點,從而有針對性地進行引導,帶領學生走出思維誤區.在教學中,只有理解學生才能設計出符合學生最近發展區的問題,才能帶領學生走出“題海”,提高教學效率.

3 理解教學

教學絕不是簡單的知識傳授,“教”與“學”應該是有機的相互促進、協調統一的整體.在教學中,過多強調“教”的意義而忽視“學”的價值,將影響教學的發展.在教學中,教師不僅要清楚知識的邏輯結構,還要清楚學生的思維特點和認知規律,同時還要掌握科學的教學方法,將“教”與“學”有機地整合在一起,將有邏輯意義的新舊知識相串聯,進而通過不斷吸收和同化形成清晰、穩定的認知結構.

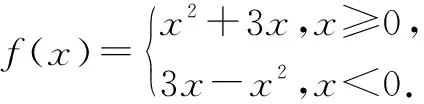
(1)若f(2-a2)>f(a),求實數a的取值范圍;

(2)若f(2-a2)+f(a)>0,求實數a的取值范圍.

設計意圖：借助綜合情境,考查學生應用單調性解決問題的能力.第一問可直接利用函數的單調性進行求解;第二問利用奇函數轉化為f(2-a2)>f(-a),結合單調性來求解,雖然形式發生了變化,但其本質卻沒有變.

數學題目千變萬化,若能抓住問題的本質,往往可以在變化中找到一些不變的規律.這正是數學學習的樂趣之所在,也是數學教學的價值所在.

總之,以“三個理解”為出發點,讓數學知識的發生、發展順應學生的思維發展,這樣的教學是自然流暢的,既有活力又高效.