合理創新設計,優化教學效果
——基于“導數及其應用”的大單元教學

劉雪亮

? 江蘇省揚州市江都區育才中學

在“導數及其應用”的大單元教學中,為了有效優化教學效果,筆者以習題課的形式展開復習,對大單元教學與復習進行大膽創新與嘗試,具體的教學設計分為四個環節.

1 引導回憶,構建體系

首先帶領學生通過回憶的形式,構建知識網絡體系,如圖1所示.

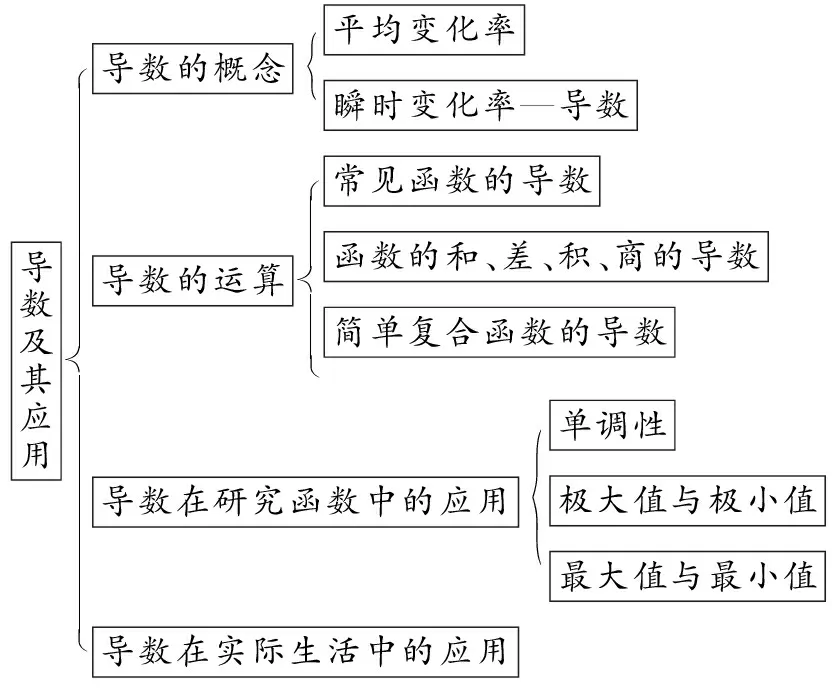
圖1

2 知識要點,技巧方法

2.1 知識回顧

(1)導數的幾何意義.

(2)導數的基本運算法則,求導的常見技巧方法.

(3)導數的基本應用:與幾何意義、單調性、極值(或最值)以及實際應用等有關的問題.要注意的是,導數常常與不等式、方程等有機結合,形成綜合性試題.

(4)利用導數解決實際應用問題時,首先要注意自變量的取值范圍,即考慮問題的實際意義.在應用問題的設計上,高考多設置為單峰函數,以降低要求.

(5)高考對本單元的考查要求:會利用函數與導數知識來處理導數的幾類基本應用問題.

2.2 技巧方法

函數與導數問題中,主要涉及求解函數的單調區間、可導函數的極值、函數的最值等的技巧方法與基本步驟,這里略.

特別在解決問題中,一定要注意正確把握函數的極值與函數的最大(小)值之間的聯系與區別,不能混淆.函數的極值是函數的局部性質,而函數的最大(小)值是相對整個定義域而言的.求在閉區間[a,b]上連續函數f(x)的最大(小)值時,需要注意開區間(a,b)內極大(小)值與端點函數值f(a),f(b)的比較.

3 主題串講,綜合提高

3.1 導數的運算

導數運算求值問題中,在函數求導時,應仔細觀察和分析函數的結構特征,緊扣導數的四則運算法則以及基本函數的求導公式,有時還要適當等價變形.

例1已知函數f(x)=(2x+1)·ex,f′(x)為f(x)的導函數,則f′(0)的值為______.

分析：利用積的求導法則對函數求導,代入即可解決相應的求值問題.

解析：對函數f(x)求導,得f′(x)=(2x+3)ex.

所以f′(0)=(2×0+3)·e0=3.

故填答案:3.

點評：本題考查導數的運算,屬于基礎題型,熟練掌握對應的導數公式與運算法則是關鍵.

3.2 導數的幾何意義

導數的幾何意義及其應用是函數與導數部分的一個重要考點,能夠有機“串聯”起函數、導數、平面解析幾何等相關知識,成為高考中比較常見的一個基本考點,往往涉及與切線有關的綜合應用等.

例2已知f(x)為偶函數,當x≤0時,f(x)=e-x-1―x,則曲線y=f(x)在點(1,2)處的切線方程為______.

分析：根據題設條件,結合函數的基本性質,先確定x>0時函數的解析式,再利用導數的幾何意義求切線的斜率.

解析：當x>0時,―x<0,則f(―x)=ex-1+x,又f(x)為偶函數,所以f(x)=f(―x)=ex-1+x.

當x>0時,f′(x)=ex-1+1,則在點(1,2)處的切線斜率為k=f′(1)=2.

所以切線方程為y―2=2(x―1),即y=2x.

故填答案:y=2x.

點評：本題考查了函數的奇偶性,函數的解析式,導數的幾何意義,直線的方程.此類問題主要考查導數的幾何意義及其綜合應用問題,關鍵在于挖掘問題的本質與內涵,綜合利用相關的知識來分析與應用.其實,本題還可以利用函數的對稱性直接求切線斜率.

3.3 函數的基本性質

函數的基本性質問題,往往是基于函數的單調性加以拓展與綜合,特別是函數的極值與最值等,為深入研究函數的基本性質提供條件.

例3(2023年高考數學全國乙卷理科·16)設a∈(0,1),若函數f(x)=ax+(1+a)x在(0,+∞)上單調遞增,則a的取值范圍是______.

分析：借助導數,將函數f(x)的單調性問題有效轉化為f′(x)≥0在區間(0,+∞)上恒成立問題,通過不等式的求解來確定參數的取值范圍.

解析：由函數f(x)=ax+(1+a)x在(0,+∞)上單調遞增,可得

f′(x)=axlna+(1+a)xln(1+a)≥0.

①

在(0,+∞)上恒成立.

令函數g(x)=axlna+(1+a)xln(1+a),可得g′(x)=axln2a+(1+a)xln2(1+a)>0.

所以,函數f′(x)在(0,+∞)上單調遞增.

當f′(0)=lna+ln(1+a)≥0,即ln [a(1+a)]≥0,亦即a(1+a)≥1時,①式在(0,+∞)上恒成立.

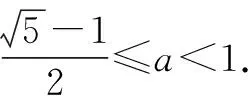
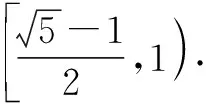
點評：將函數的單調性問題轉化為對應的不等式恒成立問題,這是解決問題的關鍵,其中融入函數與導數的應用,以及導數的運算等.正確構建不等式是解決問題的重點與難點,也是問題突破的靈魂之處,要加以靈活掌握,同時要注意等價轉化與正確構建.

3.4 函數的綜合應用

函數與導數的綜合應用問題是歷年高考中的主要考點,綜合性強,交匯性高,成為全面考查考生數學關鍵能力與基本素養的重要載體之一,要引起高度重視.

例4〔2024年重慶市開州中學高三(上)月考數學試卷〕設函數f(x)=2lnx-mx2+1.

(1)討論函數f(x)的單調性;

(2)當m=1時,若在f(x)的定義域內存在兩實數x1,x2,滿足x12.

分析：(1)通過確定函數的定義域,利用參數的分類討論,研究導函數的正負取值情況,進而判斷函數f(x)的單調性.(2)利用函數的單調性,結合對稱構造法構建新函數,利用新函數的單調性的判斷與性質來分析與證明對應的不等式.

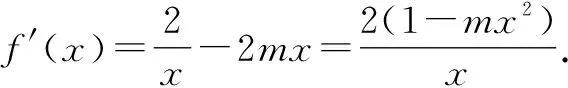
當m≤0時,f′(x)>0,則f(x)在區間(0,+∞)上單調遞增.

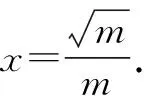
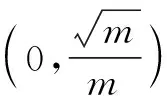
(2)證明：當m=1時,f(x)=2lnx-x2+1.

由(1)知f(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減.

又實數x1,x2滿足x1

當0

所以F(x)在(0,1)上單調遞增.

所以?x∈(0,1),都有F(x)

又0

又1<2-x1<2,x2>1,f(x)在(1,+∞)上單調遞減,所以x2>2-x1,即x1+x2>2.

點評：在解決一些涉及函數與不等式綜合應用問題時,或證明不等式成立,或利用不等式恒成立等,都可以很好地把函數與導數的綜合應用、不等式等相關知識合理交匯與融合,進而借助導數思維來分析與處理,巧妙實現問題的破解.

4 方法指導,提煉思想

導數及其應用蘊涵著豐富的數學思想,涉及一般與特殊、類比等數學思維方法:

(1)轉化與化歸思想在導數及其應用中主要用來解決有關不等式恒成立、函數的單調性等問題.

(2)函數與方程思想在導數及其應用中主要用來解決生活中的優化問題以及構造函數證明等式或不等式.

(3)分類討論思想在導數及其應用中主要用來求解單調區間、參數范圍、極值、最值以及不等式恒成立問題等.

(4)數形結合思想在導數及其應用中主要用來解決有關方程的根的問題.