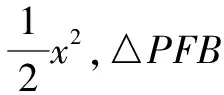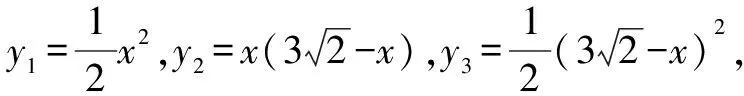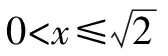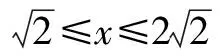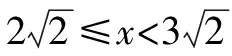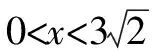運用轉化思想解決初中函數應用題
? 江蘇省蘇州市高新區實驗初級中學 陳 惠
近幾年各地的中考數學試題中,出現了一些設計新穎、貼近生活、反映時代特點的函數應用題.實際問題來源于生活,這些問題的解答要依賴于眾多的數學思想和答題技巧.如函數思想、方程思想、數形結合思想和轉化思想,其中轉化思想貫穿解題的始終[1].具體來說,就是把具體實際問題轉化為數學中的函數問題,把眾多的變量(未知量)轉化成用一個變量(或已知量)來表示,把復雜問題轉化成一個或多個簡單問題.
1 題型一:利用一次函數求最值類實際應用題
獲取最大利潤問題就是求函數的最值類問題,解決這類題的實質就是建立數學模型和求解數學模型的思維活動過程.主要運用轉化思想,將實際問題和數學問題相互轉化,使問題得以解決,解題思路如圖1:
例1(2022年江蘇省蘇州市中考試題第25題)某水果店經銷甲、乙兩種水果,兩次購進水果的情況如表1所示:
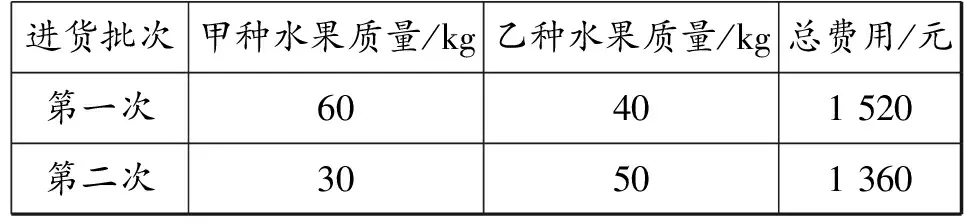
表1
(1)求甲、乙兩種水果的進價;
(2)銷售完前兩次購進的水果后,水果店決定第三次購進甲、乙兩種水果共200 kg,且投入的資金不超過3 360元.將其中的mkg甲種水果和3mkg乙種水果按進價銷售,剩余的甲種水果以17元/kg、乙種水果以30元/kg的價格銷售.若第三次購進的200 kg水果全部售出后,獲得的最大利潤不低于800元,求正整數m的最大值.
解析:(1)設甲種水果的進價為a元/kg,乙種水果的進價為b元/kg.
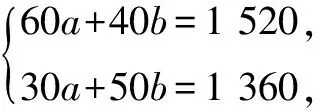
(2)設水果店第三次購進甲種水果xkg,則購進乙種水果(200-x)kg.
根據題意,得12x+20(200-x)≤3 360,解得x≥80.
設所得利潤為w元,則w=(17-12)×(x-m)+(30-20)×(200-x-3m)=-5x-35m+2 000.
當x=80時,w取得最大值-35m+1 600.
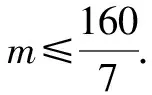
所以正整數m的最大值為22.
評析:本題主要考查一次函數的實際應用,解答本題的關鍵是在理解題意的基礎上,找出等量關系,列出相應的二元一次方程,寫出相應的函數解析式,再利用一次函數的性質求最值.
2 題型二:二次函數與幾何相結合的實際應用題
這類問題綜合性較強,既考查學生對各種幾何圖形、二次函數性質等的掌握情況,又側重考查學生的實際動手操作能力.解決這類問題主要是運用轉化思想,因此熟練掌握各種轉換技巧顯得十分重要.
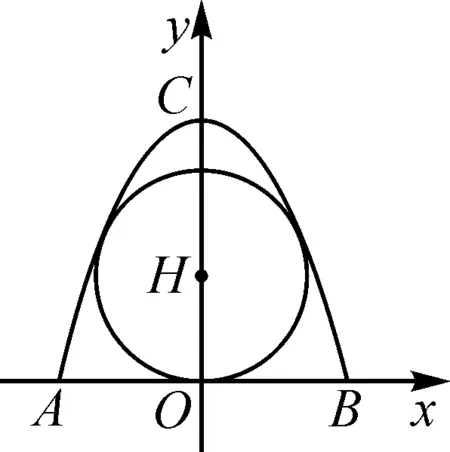
例2(2022年江蘇省揚州市中考試題第27題)如圖2是一塊鐵皮余料,將其放置在平面直角坐標系中,底部邊緣AB在x軸上,且AB=8 dm,外輪廓線是拋物線的一部分,對稱軸為y軸,高度OC=8 dm.現計劃將此余料進行切割.
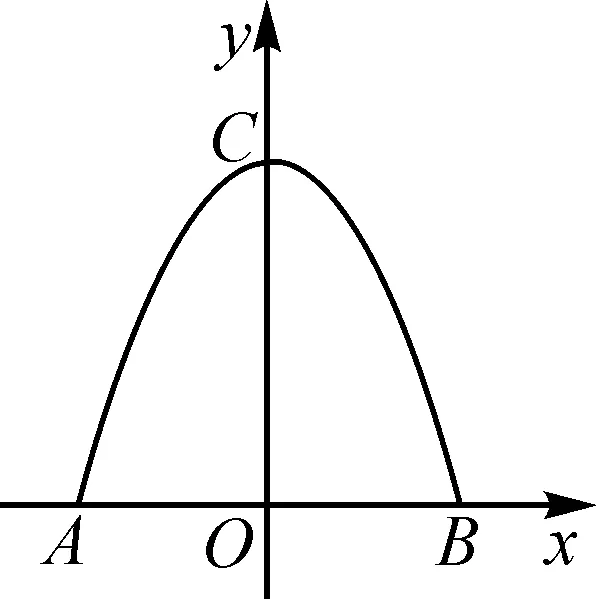
圖2
(1)若切割成正方形,要求一邊在底部邊緣AB上且面積最大,求此正方形的面積;
(2)若切割成矩形,要求一邊在底部邊緣AB上且周長最大,求此矩形的周長;
(3)若切割成圓,判斷能否切得半徑為3 dm的圓,請說明理由.
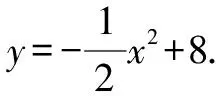
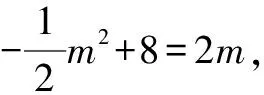
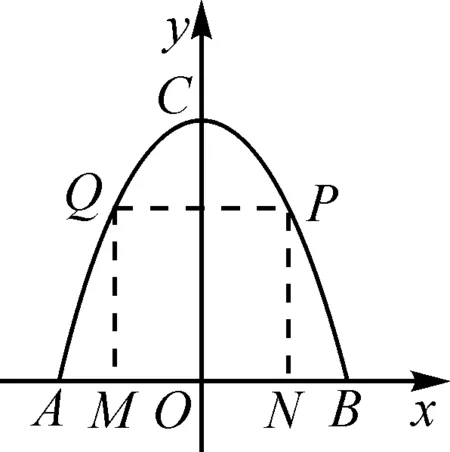
圖3
(2)如圖4所示,矩形DEFG為符合題意的矩形.設DE=2n,則E(n,0)(0 圖4 故當n=2時,矩形的周長最大,最大值為20 dm. 圖5 所以,能切得半徑為3 dm的圓. 評析:本題考查了二次函數與正方形、矩形、圓等幾何圖形相結合的綜合性問題,突出實踐操作能力.熟練掌握各圖形的性質,能靈活運用坐標與線段長度之間的轉換是解題的關鍵. 探索性問題是指根據已知條件(或給出的結論),探求相應結論(或條件)是否存在的一類問題.這類問題的解題思路是:假設存在—分類演繹推理—得出結論(合理或矛盾). 圖6 (1)設CF=x,用含有x的代數式把Rt△AEP,Rt△PFB及矩形ECFP的面積表示出來; (2)是否存在這樣的點P,使Rt△AEP,Rt△PFB及矩形ECFP的面積都小于4? 評析:本題考查了由給出結論探究點P的存在性問題.題中滲透了函數、數形結合、從特殊到一般、類比等數學思想方法.由于圖形(點、線)的位置不同,會使結論產生多種情況,這時就要分類討論,從面積相等的特殊情形到面積不等的一般情形. 運用轉化思想解決與函數有關的實際問題,具有“化陌生為熟悉、化復雜為簡單、化抽象為具體”的巨大優越性[2],能夠幫助我們理清解題思路,快速找到解題的突破口,從而降低題目的難度系數,引領我們走出解題困境.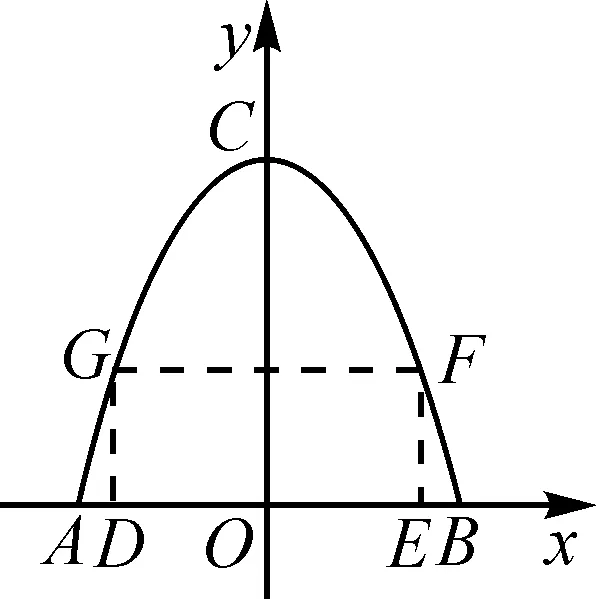
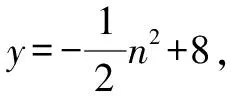

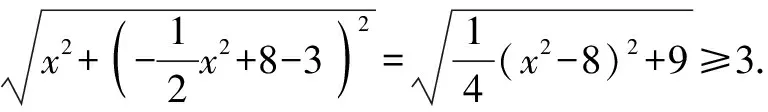
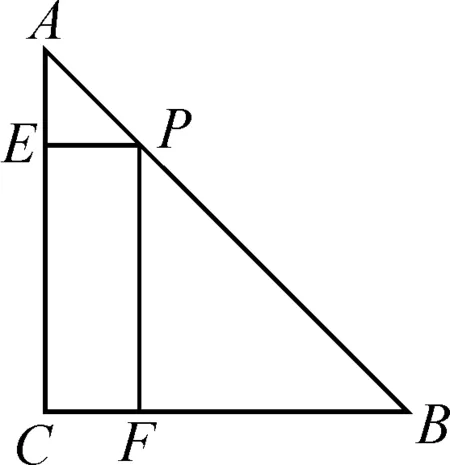
3 題型三:二次函數的探索性問題