疊船運輸方式下的半潛船耐波性分析
王 輝, 羅文嘉, 湯曉勇, 馬艷琳, 徐嘉爽, 李志勇
(1.中國石油工程建設有限公司 西南分公司,四川 成都 610095;2.大連中遠海運物流供應鏈有限公司,遼寧 大連 116001)
0 引 言
近年來,隨著海上油氣資源的開發利用,催生對大型海洋結構物的巨大需求,而這些大型海洋結構物具有超大、超重和形狀不規則等特點[1],使其海上安全運輸需求不斷提高。半潛船是運輸大型海洋結構物的特種工程船,通過調整自身壓載水改變船舶浮態,使大型結構物可順利到達半潛船的裝貨甲板,但由于半潛船裝載的結構物體積大、質量大、重心高,因此整船受風面積大,易受風浪影響。若船舶運動幅值過大或加速度過大則導致甲板上的貨物綁扎強度不夠,稍有不慎可能會造成貨物移位甚至倒塌的嚴重事故,因此,半潛船運輸過程中的耐波性研究顯得尤為重要。
有關半潛船的耐波性研究主要集中在如下各方面:零航速或非零航速下的半潛船響應幅值算子(Response Amplitude Operator,RAO)曲線;航行工況條件下的半潛船運動幅值和監測點的加速度計算;半潛船參數橫搖的影響因素;舭龍骨對半潛船橫搖的影響規律等。劉旭等[2]通過耐波性模型試驗、實船試驗和三維水動力數值模擬方法研究某50 000.00 t半潛船在不同海況條件下的水動力運動響應,獲得處于非零航速狀態的船體RAO和2個參考點的垂向與橫向加速度統計有義值。宋華寧[3]和尹艷等[4]運用SESAM軟件對目標半潛船零航速下的運動響應進行短期預報。楊洪所[5]研究不同波高、不同浪向下的半潛船六自由度運動RAO,并計算關注點的加速度。魏梟等[6]利用AQWA軟件研究不同水深、不同浪向和不同航速下的縱向多聯浮體耐波性。于本福等[7]研究波浪周期和浪向對半潛船運動響應的影響。吳波等[8]和李軍等[9]研究半潛船在不同海況條件下的運動響應和加速度規律。李曉君[10]和李曉君等[11]針對裝載重大件貨物的半潛船在長波海浪中航行時具有發生參數橫搖的風險,構建半潛船的運動模型,運用變參數分析法定量計算分析波浪長度、波浪高度、初穩心高和航速變化等關鍵因素對半潛船航行安全的影響程度和作用規律,找出誘發半潛船參數橫搖的關鍵因素。蔡連財等[12]研究舭龍骨參數對半潛船橫搖響應的影響。
綜上所述,半潛船由于運輸貨物的特殊性和運輸時間長、風浪環境多變,因此在每次運輸前均需要根據所載貨物和途經航線等進行具體的耐波性計算分析。疊船運輸方式,即半潛船甲板承載雙駁船浮托的井口平臺,具有更大的挑戰性與危險性。以疊船運輸方式下的半潛船為研究對象,采用AQWA軟件,基于勢流理論,對該船在不同航速、不同吃水和不同海況條件下的運動響應規律進行研究,并計算相關參考點運動幅值和加速度,為半潛船貨物的安全綁扎提供設計依據。
1 理論基礎
1.1 疊船運輸方式下的半潛船運動響應
假定疊船運輸方式下的半潛船在一定航速下的流場為無黏性、無旋轉和不可壓縮的理想流體,則流場的運動可采用三維勢流理論描述,浮體結構在波浪中的波浪激振力Fwj由入射波和繞射波引起,其表達式[6]為
Fwj=Fwj,k+Fwj,d=Re[(fwj,k+fwj,d)]e-iwt
(1)
式中:j為第j階運動模態,在j=1,2,…,6時Fwj分別為縱蕩力、橫蕩力、垂蕩力、橫搖力矩、縱搖力矩和艏搖力矩;Fwj,k和fwj,k為第j個自由度的弗勞德·克雷洛夫力;Fwj,d和fwj,d為第j個自由度的繞射力;Re[]為取[]內復數變量的實部。
(2)
式中:ρ為浮體所處流場中的流體密度;S為浮體結構表面面積:S0為浮體結構在水中的濕表面面積;φI為入射波速度勢;φD為繞射速度勢;nj為浮體各自由度的法向量;U為航速。
由輻射勢引起的輻射力Fj的表達式為
(3)
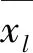
uj,l和λj,l的表達式為
(4)
式中:φr為物體激蕩的輻射勢。
浮體的頻域運動方程為
(5)
式中:m為浮體的質量矩陣;u為以uj,l為元素的附加質量矩陣;λ為以λj,l為元素的附加阻尼矩陣;k為靜水恢復力矩陣;x為浮體的運動響應幅值算子列陣;Fw為浮體所受的以Fj為元素的波浪激振力列陣。
求得式(4)的附加質量與附加阻尼和式(1)的波浪激振力,代入式(5),即可求得疊船運輸方式下的半潛船運動響應。
1.2 疊船運輸方式下的半潛船短期最大值預報
對于一個給定的波浪譜S(ω),疊船運輸方式下的半潛船水動力載荷的波頻運動響應譜SR(ω)的表達式[13]為
SR(w)=RAO2S(w)
(6)
根據響應譜得到的第n階矩的表達式為
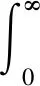
(7)
式中:mnR為運動方差。
一般認為短期海況符合窄帶瑞利分布,浮體的波頻運動近似認為同樣符合瑞利分布。對于短期海況時間t,浮體波頻運動次數為t/T1R次,出現的最大值所對應的超越概率為發生次數的倒數T1R/t,則浮體運動最大值Rmax為
(8)
1.3 疊船運輸方式下的半潛船加速度預報
疊船運輸方式下的半潛船貨物綁扎設計監測點的三向加速度表達式[9]如下:
縱向加速度為
alongi=xG-(yP-yG)ψ+(zP-zG)θ-gsinθ
(9)
橫向加速度為
atrans=(xP-xG)ψ+yG-(zP-zG)φ-gsinθ
(10)
垂向加速度為
avert=-(xP-xG)θ+(yP-yG)φ+z
(11)
式(9)~式(11)中:z、φ、θ和ψ分別為垂蕩、橫搖、縱搖和艏搖的幅值;xG、yG和zG分別為疊船運輸方式下的半潛船重心G的縱向、橫向和垂向坐標;xP、yP和zP分別為貨物綁扎設計監測點P的縱向、橫向和垂向坐標;g為重力加速度。
2 AQWA軟件可靠性驗證
為保證AQWA計算耐波性結果的可靠性,采用具有公開試驗數據結果的DTMB5512標準模型[14]進行耐波性計算,包括縱搖運動和垂蕩運動,計算工況為規則波中零航速下的迎浪狀態。DTMB5512標準模型主尺度如表1所示。采用CATIA軟件建立DTMB5512的三維模型,如圖1所示。將三維模型導入AQWA,設置浮體質量、阻尼和水動力計算參數并進行網格劃分,對三維模型進行水動力計算,計算結果如圖2所示。由圖2可知:AQWA計算值與試驗值曲線的趨勢基本一致且相對誤差較小,驗證AQWA軟件計算耐波性的可靠性和有效性。

表1 DTMB5512標準模型主尺度

圖1 基于CATIA的DTMB5512三維模型
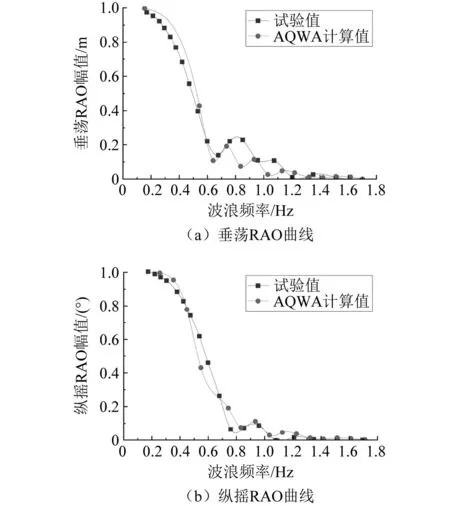
圖2 DTMB5512三維模型水動力計算結果
3 計算模型和載況
疊船運輸方式下的半潛船具體載況如下:2艘駁船(自艉部開始,分別為駁船1與駁船2)浮托1個井口平臺(坐落于雙駁船上)組成聯合體,該聯合體疊放在半潛船甲板上。疊船運輸方式下的半潛船三維模型如圖3所示。AQWA系統計算的坐標系如圖4所示,其中,坐標原點位于船舶中縱剖面與水線面交線和艉垂線的交點處,自原點指向艏部為x軸正向,左舷為y軸正向,水面垂直向上為z軸正向。
圖3 疊船運輸方式下的半潛船三維模型
圖4 坐標系定義
半潛船主尺度如表2所示。該船與裝載貨物(2艘駁船和1個井口平臺)的質量重心和慣性半徑如表3所示,其中,Rxx、Ryy和Rzz分別為對應各坐標軸的慣性半徑。由于該船的最大載重量為60 000.00 t,而裝載貨物總質量約19 300.00 t,因此在搭載貨物后該船的吃水仍具有較大裕量。為研究吃水對耐波性的影響,設計3種吃水工況,分別為9.600 m、8.600 m和7.600 m,通過COMPASS軟件對該船進行配載,得到3種吃水對應的排水量和重心位置,如表4所示。將半潛船CATIA三維模型導入AQWA,根據表3和表4的數據進行系統參數設置和網格劃分,即可進行系統的水動力求解,其中,網格最大單元尺寸為5.000 m×5.000 m,單元總數為4 966個。
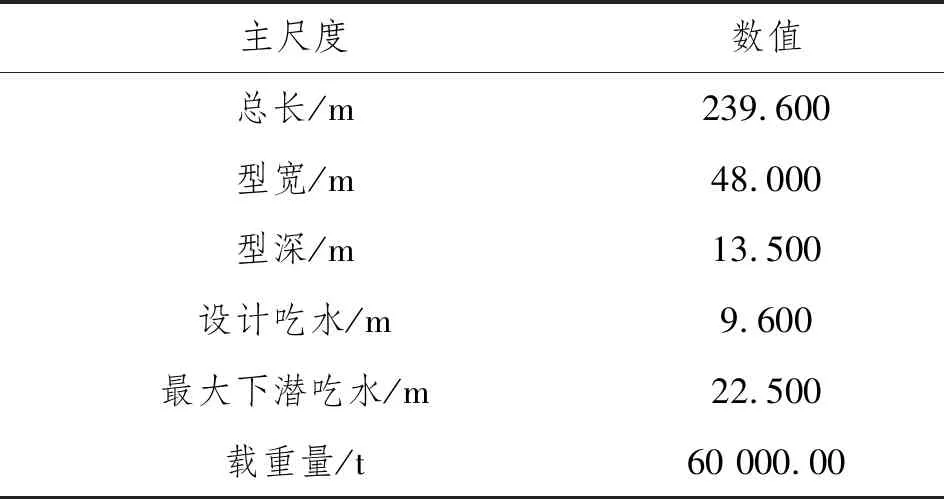
表2 半潛船主尺度

表3 半潛船與裝載貨物的質量重心和慣性半徑
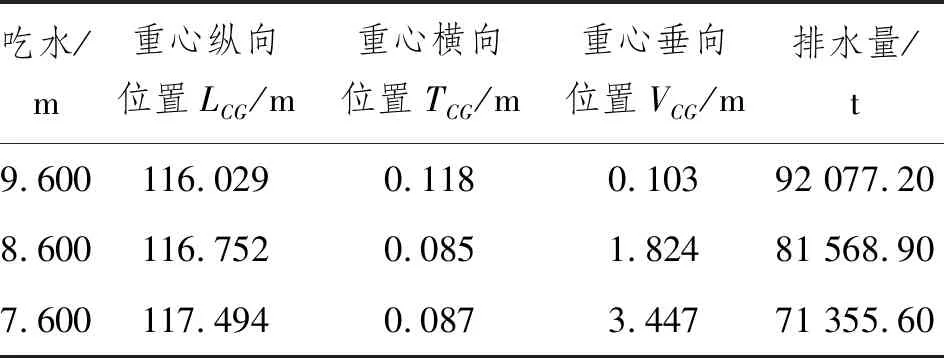
表4 半潛船裝載工況
4 疊船運輸方式下的半潛船運動響應
4.1 疊船運輸方式下的半潛船RAO
RAO等于浮體六自由度運動幅值與輸入波幅比值的平方,表示在線性波浪作用下浮體的運動響應特征。計算在滿載吃水9.600 m時浪向和航速對疊船運輸方式下的半潛船RAO的影響,找出最危險浪向,在此基礎上研究不同吃水的影響。RAO計算工況如表5所示。

表5 RAO計算工況
4.1.1 浪向和航速對RAO的影響
在滿載吃水9.600 m時,計算3個航速下的六自由度RAO,如圖5所示。
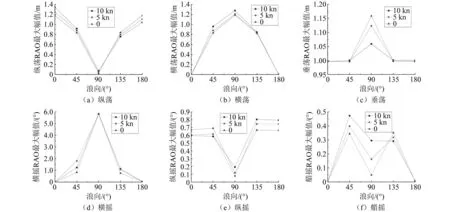
圖5 不同航速下的六自由度RAO與浪向的關系
六自由度RAO的最危險情況如表6所示,其中,橫搖最大達5.838°,縱搖最大達0.804°,垂蕩最大達1.159 m。最危險浪向下的不同航速對RAO的影響如圖6所示。
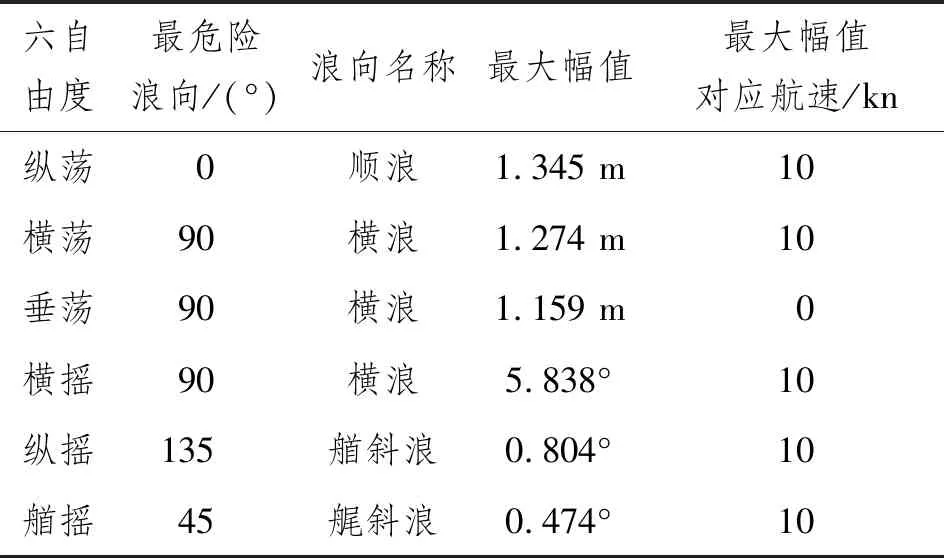
表6 RAO最危險情況
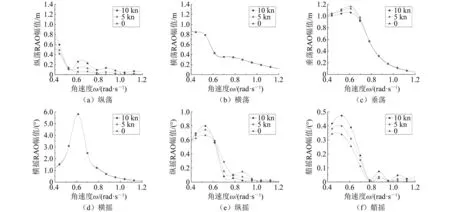
圖6 最危險浪向下的不同航速對RAO的影響
由于橫搖、垂蕩和縱搖對疊船運輸方式下的半潛船影響更大,因此重點分析這3個自由度在最危險浪向下和不同航速下的RAO幅值變化規律。
(1)橫搖:橫搖RAO幅值最明顯,基本不隨航速變化,這與浪向為90°時波浪頻率等于自然頻率、波浪頻率不隨航速變化的規律一致。
(2)垂蕩:在角速度ω<0.70 rad/s即周期T>8.95 s時,航速增大,垂蕩RAO幅值隨之有所減小,其他頻段垂蕩RAO幅值不隨航速變化。
(3)縱搖:角速度ω<0.60 rad/s即周期T>10.50 s時,航速增大,縱搖RAO幅值隨之有所增大,其他頻段隨航速增大,縱搖RAO幅值減小。
4.1.2 吃水對RAO的影響
根據表6,計算在最危險浪向下和最大幅值對應航速下不同吃水工況(分別為9.600 m/8.600 m/7.600 m)的RAO幅值變化規律,如圖7所示。
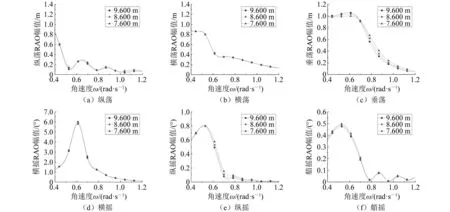
圖7 最危險浪向和最大幅值對應航速下的不同吃水工況對RAO的影響
(1)橫搖:橫搖RAO幅值變化最大,在角速度ω=0.62 rad/s(即周期T=10.13 s)時達最大值,且吃水增大,橫搖RAO幅值減小;其他頻段橫搖RAO幅值對吃水變化不敏感。
(2)垂蕩:在角速度ω<0.70 rad/s(即周期T>8.95 s)時,吃水增大,垂蕩RAO幅值隨之增大;在角速度ω>0.70 rad/s時,吃水增大,垂蕩RAO幅值減小。
(3)縱搖:在角速度ω>0.50 rad/s(即周期T<12.56 s)時,吃水增大,縱搖RAO幅值減小;在角速度ω<0.50 rad/s時,縱搖RAO幅值不隨吃水變化。
4.2 疊船運輸方式下的半潛船在不規則波中的短期預報
4.2.1 航線環境條件與計算工況
運輸航線為自中國某港口至中東某港口,根據航線與全球航區劃分,途經28、41、40、62、61、60、50、39和38航區。根據GWS全球海洋波浪統計數據庫,各航區10 a最大有義波高如表7所示。
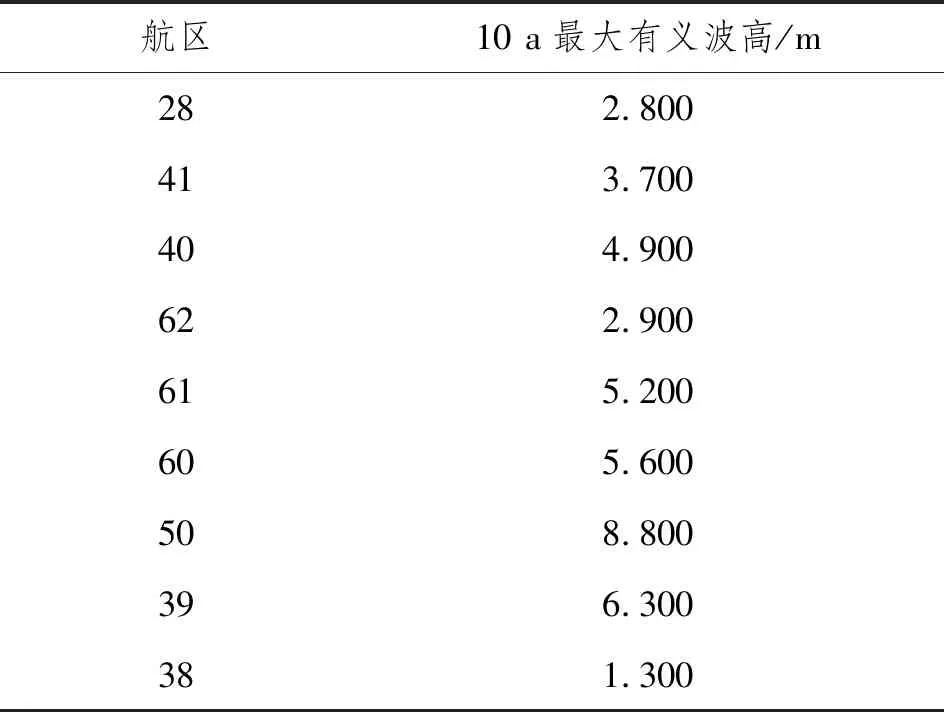
表7 各航區10 a最大有義波高
根據上述資料,該航線10 a最大有義波高為8.800 m,設置3個不同海況,即3個不同的有義波高(Hs),計算工況如表8所示。計算貨物綁扎設計關鍵點的加速度,監測點位置分別為雙駁船的重心處和井口平臺重心處,具體數值如表3所示。
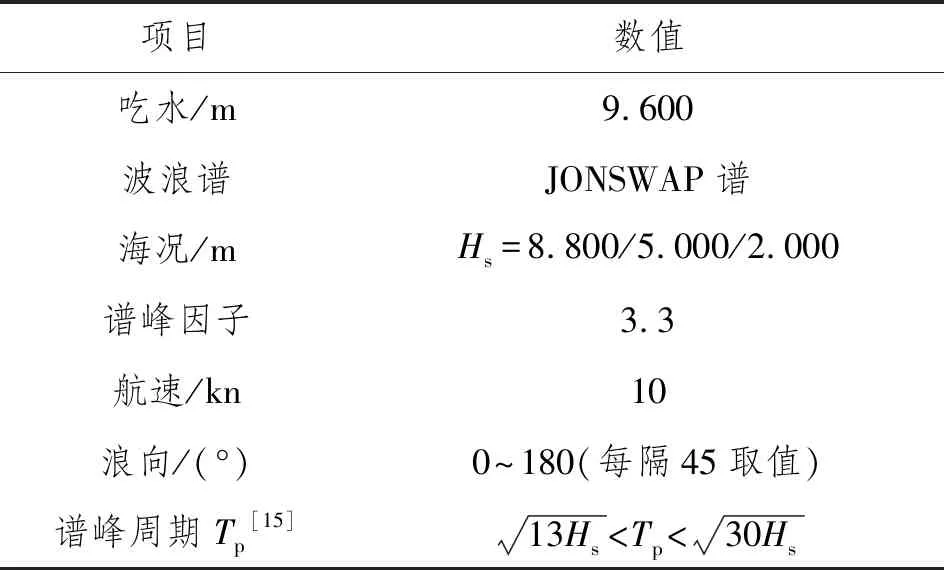
表8 計算工況
根據文獻[15],對于帶有冗余推進系統的自航式半潛船,對不同浪向下的有義波高進行折減,如表9所示。不同有義波高下的環境組合工況如表10所示。

表9 波高折減表
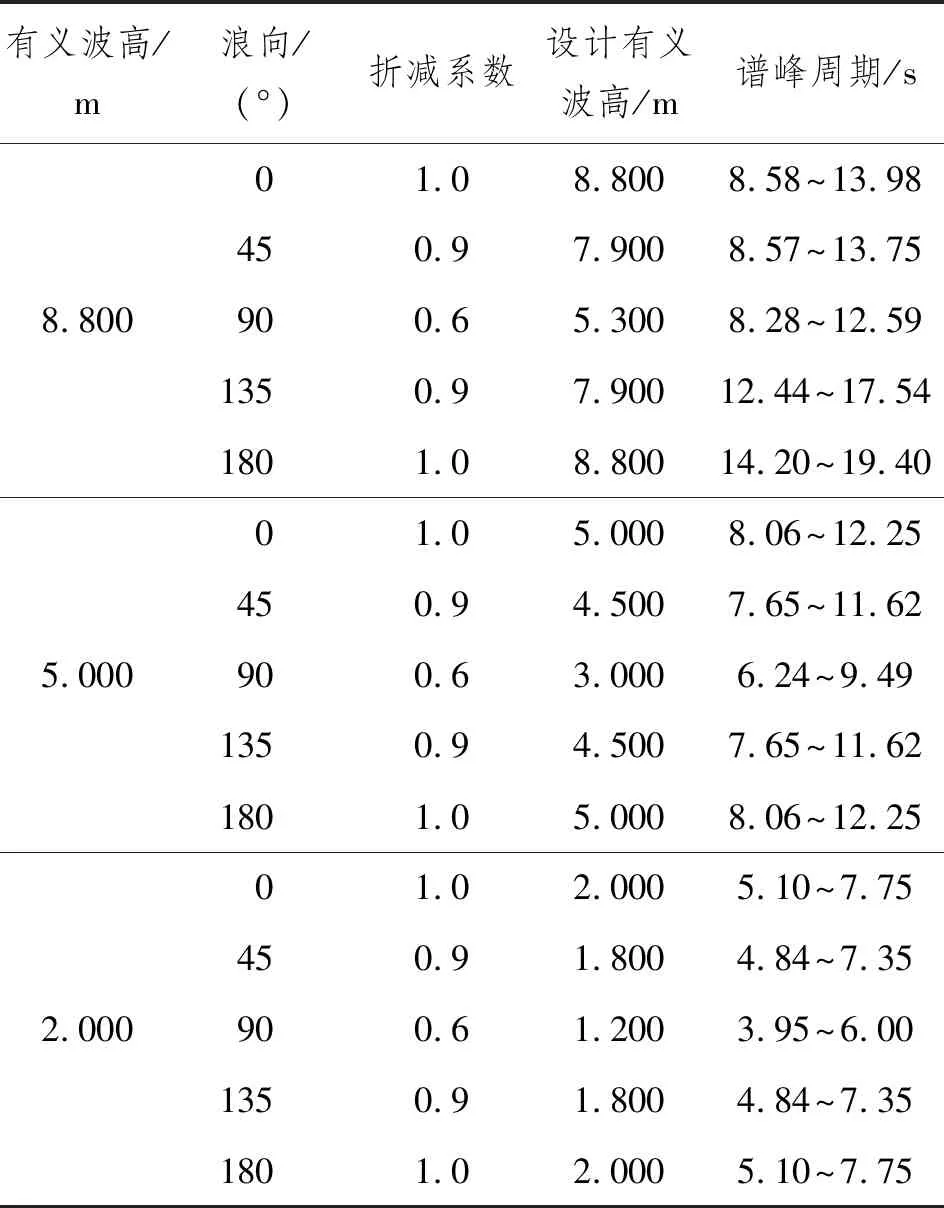
表10 環境組合工況
4.2.2 在不規則波中的運動響應
根據表10的環境組合工況進行計算,得到重心處六自由度運動響應最大值,如表11所示。隨著有義波高增大,橫搖運動幅值變化最大,每增大單位有義波高,橫搖角平均增大2.88°;其次是垂蕩運動,每增大單位有義波高,垂蕩幅值平均增大0.850 m;最后是縱搖運動,每增大單位有義波高,縱搖角平均增大0.79°。
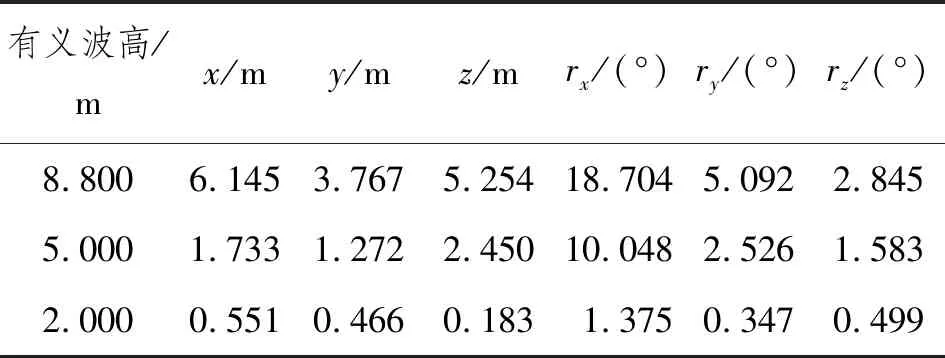
表11 不同有義波高下的重心處六自由度運動響應最大值
貨物綁扎設計監測點在上述海況條件下的橫向、縱向和垂向加速度,如表12和圖8所示。由圖8可知:對于半潛船和2艘駁船,垂向加速度隨有義波高變化最敏感,縱向加速度變化幅度最小;井口平臺重心較高,變化最大的是橫向加速度。一般在干拖運輸航行過程中,對船舶橫向加速度比較關注。海洋工程要求干拖運輸在較大波浪條件下的最大橫向加速度為0.5g[8]。疊船運輸方式下的半潛船在不同海況的計算結果中,貨物綁扎設計監測點橫向加速度的最大值為3.638 m/s2,小于0.5g,符合要求。
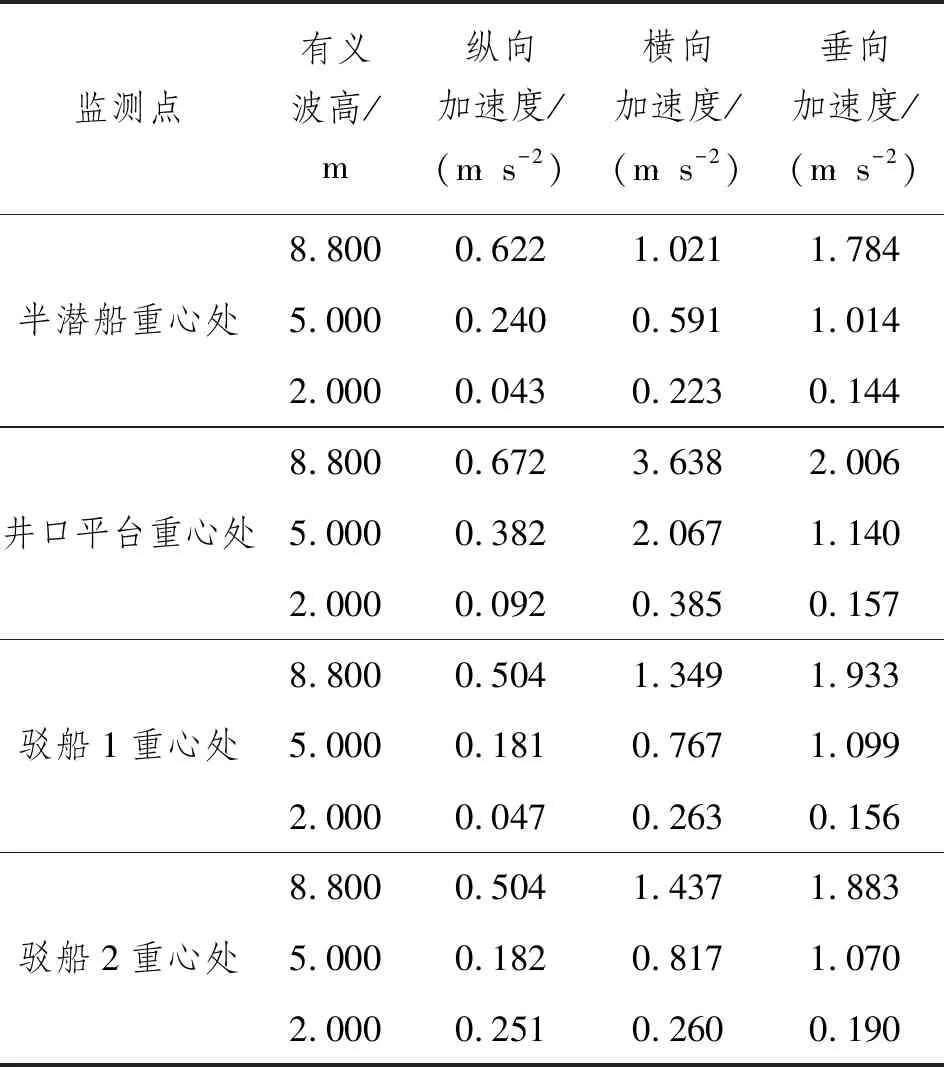
表12 貨物綁扎設計監測點的加速度
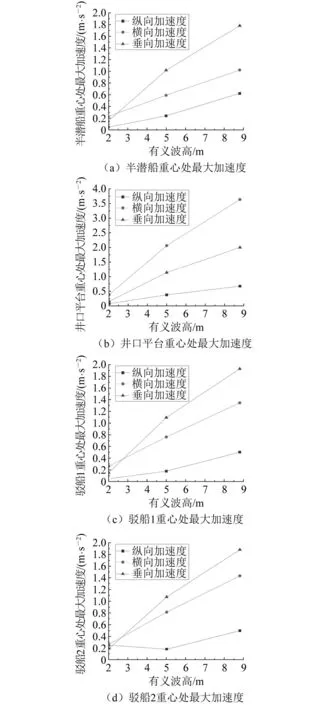
圖8 貨物綁扎設計監測點的最大加速度
5 結 語
對疊船運輸方式下的半潛船進行水動力分析,分別計算重心處的RAO幅值和不規則波中的運動幅值與加速度。為減小RAO幅值,可適當增大航速、增大吃水,浪向保持縱浪和45°或135°的斜浪比較有利。對不規則波中的運動和貨物綁扎設計監測點的加速度進行短期預報,可為疊船運輸方式下的半潛船貨物綁扎提供設計依據。

