基于改進EMD?Kurtogram 法的滾動軸承早期故障診斷研究

趙超陽，陳 亮，韋 隆，韓思源，李培軍

（鄭機所（鄭州）傳動科技有限公司，河南 鄭州 450001）

0 引言

滾動軸承是旋轉機械設備的關鍵部件，決定了設備的使用性能[1?2]。相關數據表明，機械設備故障造成的損失極為嚴重，且旋轉機械設備的故障有近3 成是由滾動軸承故障引起的[3]。因此，開展滾動軸承早期故障診斷工作對設備可靠性的保障及避免重大經濟損失具有重要意義[4?6]。

現有的滾動軸承早期故障診斷技術普遍采用傳感設備采集到的振動信號，其早期故障診斷技術的核心機理在于：滾動軸承的不同故障類型對應著不同的故障特征頻率，通過對特征頻率與振動信號處理得到的頻率信息對比，進而判定故障發生的種類。目前，面向振動信號的信號處理技術是滾動軸承早期故障診斷技術的研究熱點之一[7]。

信號處理技術的難點在于采集振動信號的不純粹性。由滾動軸承故障部位引起的共振信號經過時頻域分析，可直接得到準確的特征頻率，但是在實際工程中，振動信號包含了背景噪聲及外界干擾等信息，使得時頻域分析很難針對有效信息而進行，因此無法得到滾動軸承準確的故障信息。降噪及共振帶的選取是提取有效故障信息的關鍵。黃文靜提出了一種利用提升小波消噪技術來提高局部均值分解分量有效性的方法，從而提高了局部均值分解方法的效率[8]。為了有效提取故障信息，Lü Y 等提出了一種多元經驗模態分解方法，該方法采用非局部均值去噪方法對采樣信號進行預處理，提取到能有效反映故障信息的本征模態分量[9]。R.Abdelkader 等改進了傳統EMD 方法，根據閾值對EMD分解的本征模態分量進行篩選與重構，在分析信號中突出故障信號[10]。馬新娜等提出了一種選取故障信息共振帶的快速譜峭度圖算法，該算法結合共振解調技術，可實現故障信息的準確診斷[11]。

綜上，為提高滾動軸承早期故障診斷的準確性，本文提出一種基于改進EMD?Kurtogram 法的滾動軸承早期故障診斷方法。首先通過峭度準則及系數準則對采樣信號EMD 處理后的信號進行重構，以削弱干擾信息的影響；接著根據快速譜峭度圖得到帶通濾波器所需要的參數，通過帶通濾波及時頻域分析得到故障頻率；最后進行實驗平臺驗證及相關算法對比，證明所提方法的有效性和先進性。

1 滾動軸承早期故障診斷技術

1.1 改進經驗模態分解法

經驗模態分解（Empirical Mode Decomposition,EMD）由美籍學者Huang 等在1998 年首次提出[3]。該方法可將復雜信號分解為一系列本征模函數（Intrinsic Mode Function,IMF）之和，再將故障沖擊明顯的IMF 分量重構為待處理信號，通過進一步包絡解調和短時傅里葉變換以提取故障特征。該方法的缺點在于：

1）有過分解的可能：在生成的系列IMF 分量中常常產生偽分量，這些偽分量會干擾正常特征頻率的提取，必須予以去除；

2）IMF 分量合成準則：選擇哪些IMF 分量合成待處理信號會影響最終的診斷精度，若選擇不合理的重構信號，會增加故障頻率提取的難度。

文獻[12]針對上述問題提出兩種準則，分別為互相關系數準則及峭度準則。互相關系數準則利用偽分量相關系數小的特點引入互相關系數指標；峭度準則利用故障沖擊信號峭度值大的特點引入峭度指標。綜合上述，對兩種準則進行濾波可達到信號去噪的目的。

1.2 譜峭度理論

峭度（Kurtosis）作為統計學上常用的無量綱指標，對沖擊特性十分敏感，但其易受噪聲信號影響而喪失穩定性與準確性，難以在實際工程中應用。為了克服上述缺陷，R.F.Dwyer 提出了譜峭度的概念，通過得到頻率譜上每根譜線的峭度值，進而分析出故障發生的具體頻率段[13]。

定義h(t,s)為時變沖擊響應函數，信號X(t)的非平穩激勵響應信號為Y(t)，Y(t)經Wold?Cramer 分解為：

式中：頻率f處信號Y(t)的時變傳遞函數H(t,f)常表達為其短時傅里葉變換后的形式：

式中：γ(τ-t)是窗函數，其寬度往往很小。基于四階譜累積量的譜峭度可定義為：

式中S2nY(t,f)為2n階順時矩。作為衡量復包絡信號的指標，S2nY(t,f)可以表達為：

綜上，譜峭度可被定義為四階譜累積量，用于表示概率密度函數H在某一頻率上的峰值大小：

1.3 快速譜峭度圖

快速譜峭度（FAST?Kurtogram）算法由學者J.Antoni首先提出[14]。如圖1 所示，快速譜峭度圖是該理論的延伸，是由譜峭度值KY(f)、頻率f及其分辨率Δf組成的二維圖。

圖1 快速譜峭度示意圖

通過對每個時域包絡信號的KY(f)依據其數值分配不同顏色深度，進而將峭度值最大的頻段信息在關于帶寬和中心頻率的網格圖上表現出來，以便后續頻譜分析。

2 基于EMD?Kurtogram 算法的故障診斷

如圖2 所示，用于早期故障探測的共振解調技術（又稱包絡解調技術）利用自身結構的諧振，將故障振動信號調制至高頻部分后包絡解調出故障特征。帶通濾波是該方法剔除無關構件的信號干擾的關鍵，然而仍然存在無法確定帶通濾波器的帶寬和中心頻率的局限。

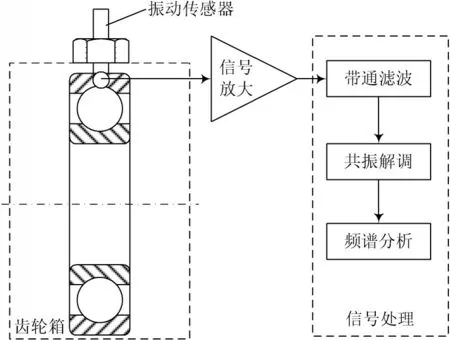
圖2 共振解調法基本原理

對于旋轉機械故障的診斷，FAST?Kurtogram 算法可以快速尋找到合適的帶通濾波器帶寬及中心頻率，彌補共振解調技術的不足。為了進一步提高故障診斷的準確性和魯棒性，結合前文提到的EMD 技術，本文提出一種基于改進EMD?Kurtogram 法的滾動軸承早期故障診斷方法，該方法的具體實現流程如圖3 所示。

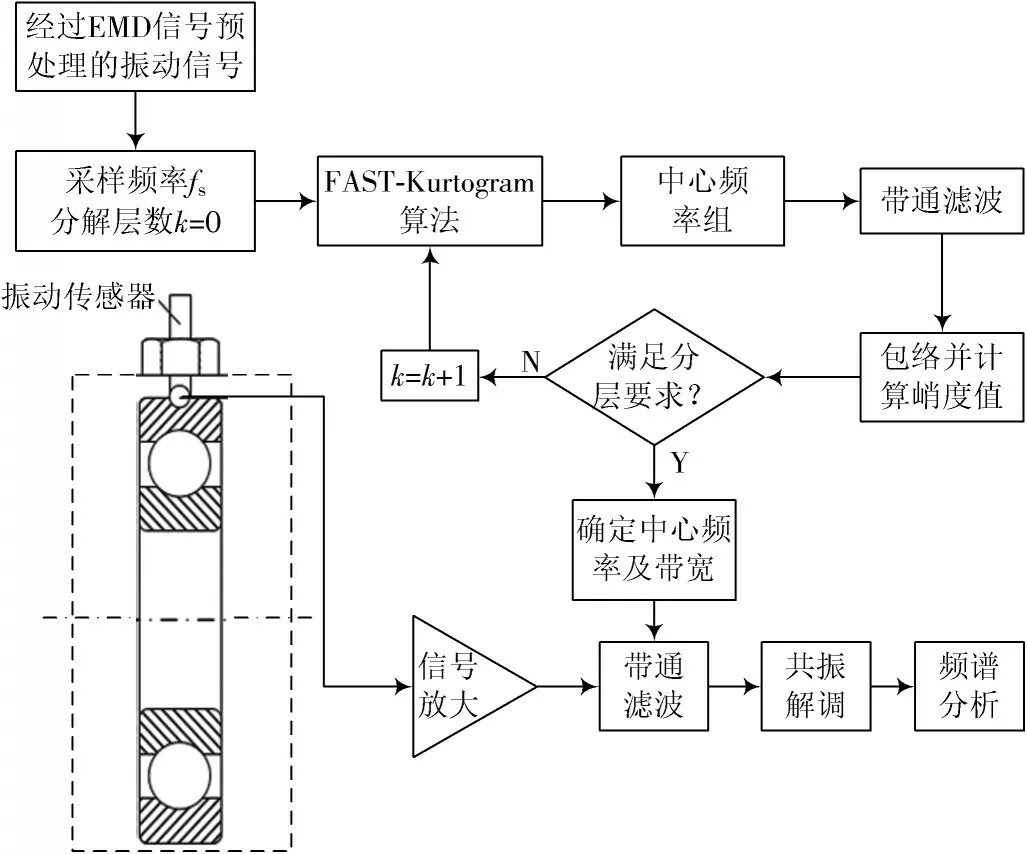
圖3 基于EMD?Kurtogram 法的早期故障診斷流程

3 實驗平臺與對比算法

3.1 實驗平臺介紹

為了驗證本文所提方法的有效性，研究樣本選擇美國凱斯西儲大學針對6205?2RS 深溝球軸承的故障數據，實驗平臺如圖4 所示。該實驗裝置采用加速度傳感器采集振動信號，基本參數如表1 所示。

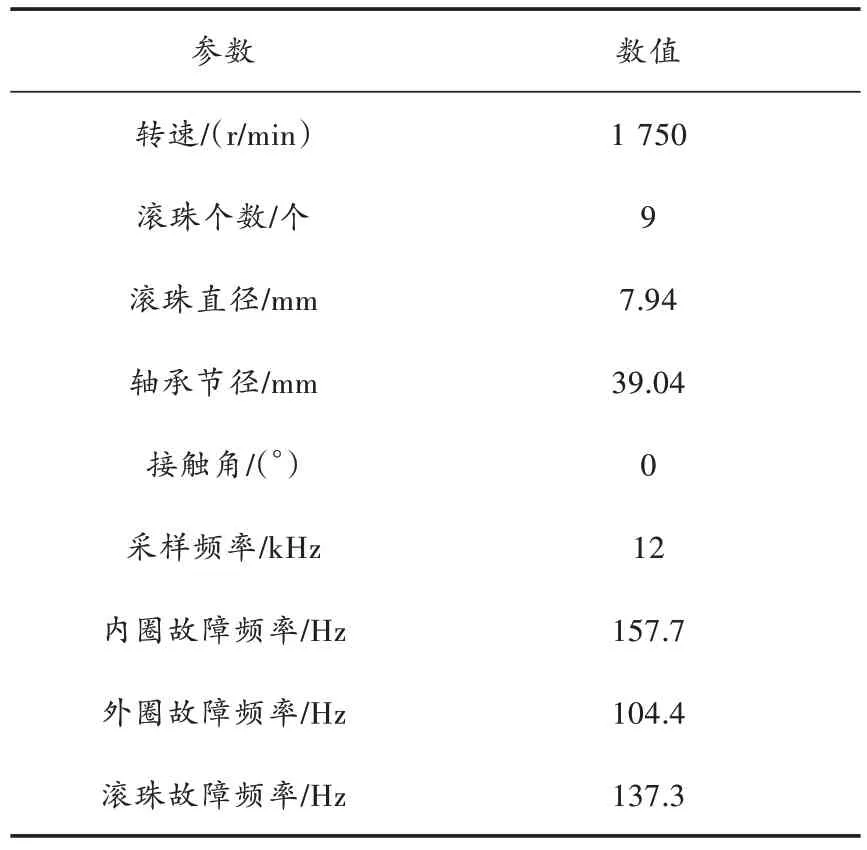
表1 滾動軸承基本參數

圖4 西儲大學實驗平臺

從表1 可以得到：對內圈而言，故障特征頻率f為157.7 Hz；外圈的故障特征頻率f為104.4 Hz。

3.2 對比算法及實驗結果分析

為了驗證本文所提方法的準確性，選擇文獻[15]提出的優化EMD 算法作為對比算法，該算法采用小波包優化EMD 的方式實現了滾動軸承的故障診斷。采用優化EMD 算法診斷滾動軸承內外圈的頻譜分析結果如圖5 所示。

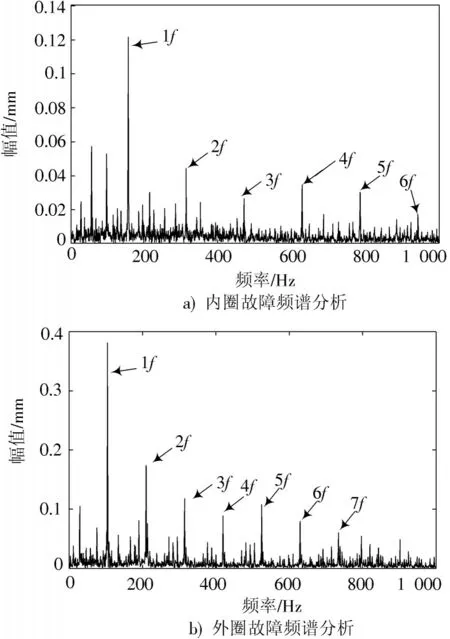
圖5 優化EMD 算法下內外圈故障頻譜分析

圖5a）、b）分別為優化EMD 算法下滾動軸承內外圈的頻譜分析圖，由圖中信息可知，經過優化EMD 算法，軸承故障信號的包絡譜較為準確地表達了內外圈故障特征頻率及其倍頻情況，可判斷內外圈是否發生故障。但圖上的干擾信息是較為嚴重的，這增加了故障特征頻率尋找的難度。從圖5a）可以看到，特征頻率在頻譜圖上并不突出；從圖5b）可以看到，外圈故障頻率前7倍頻較為清晰，該倍頻后其余高階倍頻被噪聲干擾信號掩蓋，難以找到。這表明該方法在去噪能力上仍有待提升。

圖6 給出了內外圈快速譜峭度圖，由圖中顏色較深部分頻帶信息可知，內、外圈的最優帶通濾波器參數分別為3 500 Hz、f中心=2.5 和3 000 Hz、f中心=1.5。以該參數進行帶通濾波是本文算法的關鍵。

圖6 內外圈快速譜峭度圖

帶通濾波提升了信噪比，使得振動信號中故障信號更為突出。由圖7 中本文算法下內外圈故障頻譜分析圖可以看出，故障特征頻率相較于圖5 更加直觀。其中，圖7a）的故障頻率信息更加突出且幾乎無噪聲信號頻率的干擾；相較于圖5b），圖7b）中同樣無明顯噪聲干擾。此外，外圈的8 倍頻和9 倍頻清晰可見。這表明本文方法能取得更加準確、清晰的滾動軸承故障診斷效果。

圖7 本文算法下內外圈故障頻譜分析

4 結論

為確定中心頻率參數及帶寬參數以提升最終故障診斷的質量，本文提出一種基于改進EMD?Kurtogram 法的滾動軸承早期故障診斷方法。經對比實驗驗證，可得如下結論：

1）采用該方法可尋找到帶通濾波關鍵參數，有助于實現軸承故障的準確診斷；

2）與傳統方法相比，所提方法得到的故障倍頻信息更加充分、清晰，所含噪聲干擾更少。