中國、美國、德國初中數(shù)學教材中“勾股定理”比較研究

陳書才 (郵編:241000)

安徽師范大學附屬萃文中學

董建功 (郵編:241000)

安徽師范大學數(shù)學與統(tǒng)計學院

2021年7月在中國上海舉行的第14屆國際數(shù)學教育大會(ICME-14)有一項小組專題研究,第41組(TSG41)主題是:數(shù)學學習和數(shù)學教材的資源研究與開發(fā)(www.icme14.net)．國際數(shù)學教材研究與發(fā)展會議(ICMT)已經(jīng)舉辦三屆,分別在英國南安普頓大學、巴西里約熱內(nèi)盧聯(lián)邦大學、德國帕德博恩大學召開,2022年11月14日至17日第四屆國際數(shù)學教材研究與發(fā)展會議(ICMT-4)在北京師范大學舉行．

由Springer出版的《ZDM—Mathematics Education》(簡稱ZDM)是數(shù)學教育研究領域最權威的SSCI學術期刊之一,2013年9月第5期特刊包含11文章,主題是:Textbook research in mathematics education(數(shù)學教育中的教科書研究),2018年7月第5期特刊包含15篇文章,主題是:Recent advances in mathematics textbook and development(數(shù)學教科書的最新進展與發(fā)展),2021年10月第6期特刊包含17篇文章,主題是:Mathematics Textbooks as Instruments for Change(數(shù)學教材作為變革的工具).可見,數(shù)學教科書研究已成為國際數(shù)學教育研究的熱點問題．范良火等(2013)列舉了教科書分析比較研究中的五個最常見的主題:數(shù)學內(nèi)容和主題;認知和教學法;性別、種族、公平、文化和價值問題;不同教科書的國際比較;概念和方法問題[1]．王建磐等(2018)研究了不同國家高中教科書中選擇的內(nèi)容和呈現(xiàn)方式[2]．王祎,范良火(2021)報道了一項實證研究,旨在通過比較的角度調(diào)查學生在上海和英國使用數(shù)學教科書的情況[3]．Sebastian Rezat,范良火和Birgit Pepin(2021)調(diào)查和分析了有關數(shù)學教材和課程資源作為變革數(shù)學內(nèi)容[4]．王建磐、鮑建生(2014)做了五個國家高中數(shù)學教材中例題的綜合難度的國際比較[5]．曹一鳴、吳立寶(2015)做了十個國家初中數(shù)學教材難易程度的國際比較研究[6]．吳立寶(2016)對初中數(shù)學教材的代數(shù)內(nèi)容進行了國際比較研究[7]．付鈺、張景斌(2018)進行了中美數(shù)學教材三角函數(shù)習題的比較研究[8]．覃淋(2019)進行了“中國大陸”“日本”和“中國臺灣”高中數(shù)學教材統(tǒng)計習題難度比較研究[9]．胡典順、王春靜、王靜(2020)進行了基于概念圖的中外高中數(shù)學教材比較研究[10]．

上述研究拓展了視野,指出了教材研究的主題、研究方法等,為數(shù)學教材的比較研究提供了一般的方法和技巧,對教材研究提供了一個范式．在文獻綜述的基礎上,發(fā)現(xiàn)大多數(shù)關于教材的研究立足于教材內(nèi)容,從教科書的介紹,到分析知識點的安排、例題、習題設置、習題難度等．勾股定理(又稱畢達哥拉斯定理)作為平面幾何中最基礎的定理,它是聯(lián)系數(shù)學中數(shù)與形的第一定理,導致不可公度量的發(fā)現(xiàn),揭示了無理數(shù)與有理數(shù)的區(qū)別,引發(fā)了第一次數(shù)學危機,勾股定理開始把數(shù)學由計算與測量的技術轉(zhuǎn)變?yōu)檎撟C與推理的科學[11]．鑒于勾股定理在平面幾何中的重要的地位,所以有必要對最新的國際數(shù)學教材中“勾股定理”進行比較研究．希望本研究能對中國數(shù)學課程改革、數(shù)學教材編寫、數(shù)學教育教學得到啟發(fā)．

1 研究設計

1.1 研究文本的確定

中國選取人民教育出版社的數(shù)學教科書,人民教育出版社所出的數(shù)學教材在中國具有廣泛的影響,用途較廣．美國選取霍頓·米夫林出版社(Houghton Mifflin Harcourt Publishing)2020年出版的一套數(shù)學教材,霍頓·米夫林出版社是美國最具影響力的教育出版商之一,所出版的教材受眾面較廣．德國沒有統(tǒng)一的教材,本研究選取的是由德國Klett出版社2021年出版的數(shù)學教材,該教材在巴伐利亞州廣泛使用,巴伐利亞州位于德國南部,面積70550平方公里,約占德國國土面積的五分之一,是德國幅員最大的聯(lián)邦州．三本樣本教材詳細信息見表1．

表1 樣本教材基本信息

1.2 研究框架

結(jié)合“勾股定理”的具體內(nèi)容,分別從單元整體結(jié)構、單元引入、例題分析、習題分析四個維度進行研究,具體研究框架見表2．

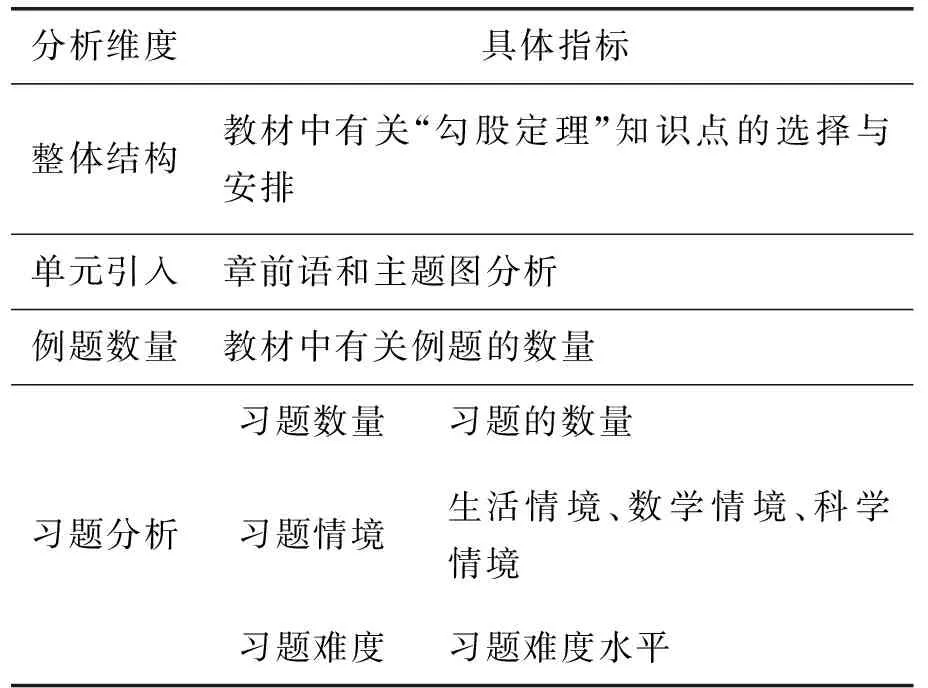
表2 研究框架

1.3 研究方法

本研究主要對中國、美國、德國三個版本初中數(shù)學教材中“勾股定理”進行比較研究,主要采用內(nèi)容分析法和比較法等研究方法．習題難度測量模型參考了已有的研究[5-9],應用范圍較廣,并根據(jù)幾何題目的特點主要從背景、推理、運算、知識含量4個難度因素進行比較,并對每個因素劃分為3個水平,并分別賦值1、2、3．見表3.

表3 習題難度測量模型

各習題難度計算方法采用以下公式計算,其中:di表示第i個習題難度因素的加權平均值;i表示第i個習題難度因素;j表示某一個難度因素所處的水平;dij表示第i個難度因素的第j個水平上的權重;nij表示這組題目中屬于第i個難度因素的第j個水平的題目的個數(shù),其總和等于該組題目的總數(shù)n．

2 研究結(jié)果與分析

2.1 三個版本數(shù)學教材中“勾股定理”整體比較

整理分析三個版本數(shù)學教材中有關“勾股定理”章節(jié)的分布年級,單元頁數(shù)和具體內(nèi)容,詳細信息見表4．

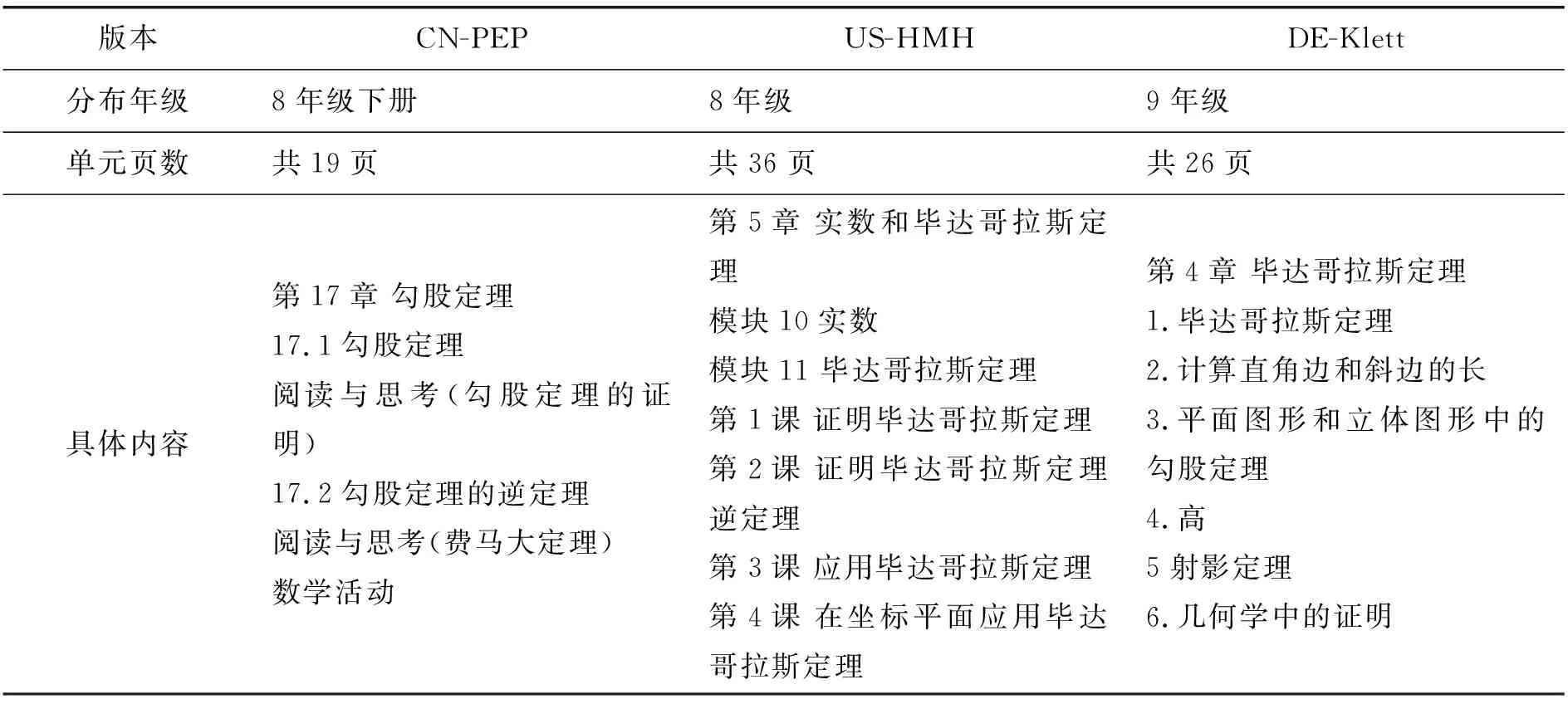
表4 “勾股定理”章節(jié)內(nèi)容整體比較

對比分析表4可以看出,三個版本教材知識的編排順序都體現(xiàn)了知識螺旋式的編排方式,都注重數(shù)學內(nèi)容的整體性、關聯(lián)性．但是三個版本教材在年級安排、內(nèi)容選擇等方面均有差異．CN-PEP版8年級下冊安排了“勾股定理”,US-HMH版在8年級第5章安排了“畢達哥拉斯定理”,DE-Klett版在9年級第4章安排了“畢達哥拉斯定理”,通過比較發(fā)現(xiàn),CN-PEP版安排了數(shù)學史知識和數(shù)學活動,說明CN-PEP教材不僅重視知識技能的培養(yǎng),也重視人文科學的培養(yǎng)．

US-HMH版單獨安排了一節(jié)在平面直角坐標系應用勾股定理,把“勾股定理”放在平面直角坐標系中去研究,并給出了距離公式．設兩個點A、B的坐標分別為A(x1,y1)、B(x2,y2),則A和B兩點之間的距離為:

兩點之間的距離公式實際上是勾股定理的一個特殊形式,即當一個直角頂點坐標為(0,0)時,勾股定理的平方項可以簡化為坐標差的平方和.說明US-HMH版教材注重幾何和代數(shù)的聯(lián)系,突出了勾股定理的距離意義,其內(nèi)容廣度更廣．DE-Klett版安排了平面圖形和立體圖形中的勾股定理和射影定理.在解決平面圖形中距離問題時,利用計算、平移、對稱等方法,運用平面上兩點之間線段最短的道理,構造直角三角形,進而利用勾股定理求解,在解決有關立體圖形中路線最短的問題,把立體圖形中的路線問題轉(zhuǎn)化為平面上的路線問題,在平面圖形中將路程轉(zhuǎn)化為兩點間的距離,然后借助直角三角形利用勾股定理求出最短距離．說明DE-Klett版注重知識之間前后的關聯(lián),注重幾何思維和邏輯推理能力的培養(yǎng),深化了勾股定理的距離意義,其內(nèi)容廣度更廣,內(nèi)容深度更深．

2.2 三個版本數(shù)學教材章首語和主題圖

章首語即章節(jié)引入語,主要作用是激發(fā)學生學習探究新知識的興趣．CN-PEP版(圖1)介紹了中國古代數(shù)學書《周脾算經(jīng)》一書上記載,在約公元前11世紀,人們就已經(jīng)知道,如果勾是三、股是四,那么弦是五．后來人們進一步發(fā)現(xiàn)并證明了關于直角三角形三邊之間的關系——兩條直角邊的平方和等于斜邊的平方,這就是勾股定理．US-HMH版(圖2)介紹了埃及的金字塔是在5000年前建造的,而建造它們的人是用數(shù)學來建造的,我們的知識在很大程度上歸功于歷史學家,我們研究過去的人、事件和思想,以及他們對當今世界的影響,歷史學家利用他們收集的信息來發(fā)展理論,并對他們的主題進行總結(jié)．DE-Klett版(圖3)介紹了古埃及的繩索拉緊器是十二結(jié)繩被十二個結(jié)分成十二條等長的繩子,第十二個結(jié)連接著繩子的起點和終點,據(jù)認為,古埃及的緊繩者在每年的洪水過后,用十二結(jié)繩來勘察田地,在建造寺廟時,這些繩索也可能被用來構建角度．通過對比發(fā)現(xiàn)三個數(shù)學版本的教材都是用數(shù)學史作為引入,幫助學生認識“勾股定理”在生活中的應用,引發(fā)學生探究勾股定理的欲望,有利于幫助學生體會數(shù)學的創(chuàng)造過程,從而培養(yǎng)學生正確的數(shù)學思維方式．

圖1 CN-PEP

2.3 三個版本數(shù)學教材中例題數(shù)量

通過統(tǒng)計例題得到CN-PEP版共有4題,US-HMH版共有6題,DE-Klett版共有12題,如圖4．通過分析可知DE-Klett版例題最多,US-HMH版例題次之,CN-PEP版例題最少．

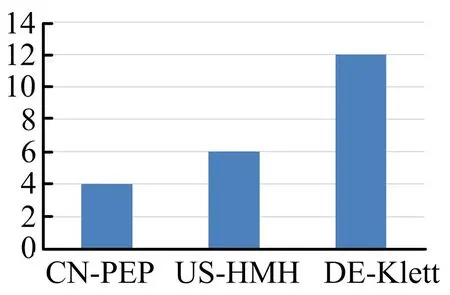
圖4 三個版本數(shù)學教材中例題數(shù)量分析

2.4 三個版本數(shù)學教材習題難度分析

根據(jù)表3給出的習題難度測量模型,分為四個維度統(tǒng)計各個難度因素中各個水平的習題數(shù)量和百分比,統(tǒng)計結(jié)果如表5所示．

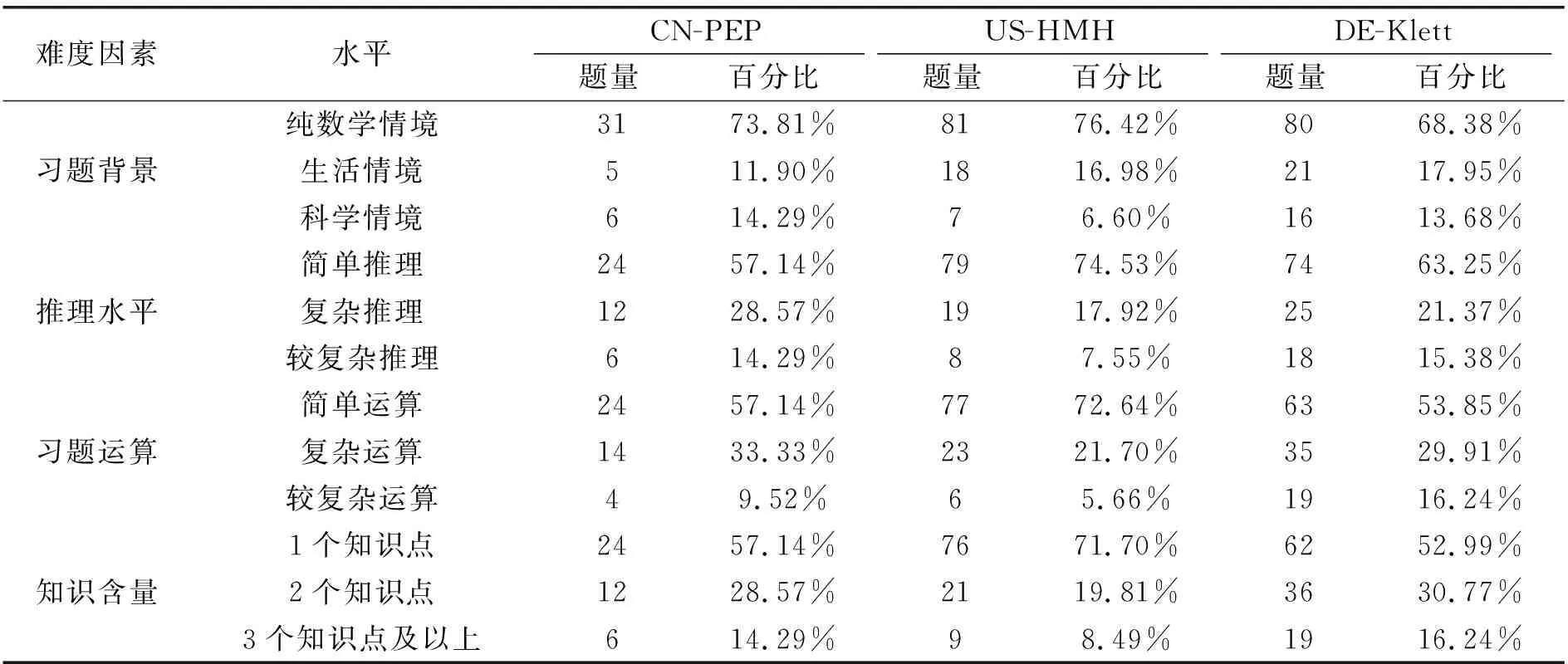
表5 三個版本數(shù)學教材難度因素比較

(1)習題背景

表5可知,三種數(shù)學教材中,“純數(shù)學情境”的習題分別占73.81%、76.42%、68.38%,“生活情境”的習題分別占11.90%、16.98%、17.95%,“科學情境”的題目分別占14.29%、6.60%、13.68%．繪制折線圖如圖5所示.

圖5 三種數(shù)學教材在習題背景因素上的比較

純數(shù)學情境,指純粹數(shù)學問題表述;生活情境,指學生熟悉的生活中的現(xiàn)象和問題;科學情境,指涉及到科學知識和其他學科融合．通過圖5發(fā)現(xiàn)三種版本數(shù)學教材中純數(shù)學習題所占比例最大,都在百分之70左右．在生活情境上,DE-Klett版所占比例最多,其次是US-HMH版,最后是CN-PEP版．在科學情境上,CN-PEP版所占比例最多,其次是DE-Klett版,最后是US-HMH版．通過對比發(fā)現(xiàn),三種教材純數(shù)學情境最多,說明三種數(shù)學教材均重視基礎知識和基本技能的培養(yǎng);其次是生活情境,說明三個版本的教材均重視學生的生活經(jīng)驗,重視數(shù)學在生活中的應用,尤其是德國DE-Klett版教材提供了大量的生活情境的圖片;最后是科學情境,說明三種數(shù)學教材均重視數(shù)學與其他學科的聯(lián)系,值得一提的是US-HMH版教材每一節(jié)習題中都有一題或兩題STEM(科學、技術、工程、數(shù)學)情境的題目．

(2)推理水平

由表5可知,三種數(shù)學教材中,“簡單推理”的習題分別占57.14%、74.53%、63.25%,“復雜推理”的習題分別占28.57%、17.92%、21.37%,“較復雜推理”的題目分別占14.29%、7.55%、15.38%．繪制折線圖如圖6所示．

圖6 三種數(shù)學教材在推理水平因素上的比較

推理的難易程度在一定程度上反映了教材的難易程度,通過圖6發(fā)現(xiàn),US-HMH版教材簡單推理最多,其次是DE-Klett版,最后是CN-PEP版,在“復雜推理”水平上,CN-PEP版所占比例多于DE-Klett版,US-HMH版所占比例最少,在“較復雜推理”水平上,DE-Klett版所占比例最多,其次是CN-PEP版,最后是US-HMH版．

(3)習題背景

由表5可知,三種數(shù)學教材中,“簡單運算”的習題分別占57.14%、72.64%、53.85%,“復雜運算”的習題分別占33.33%、21.70%、29.91%,“較復雜運算”的習題分別占9.52%、5.66%、16.24%．繪制折線圖如圖7所示．

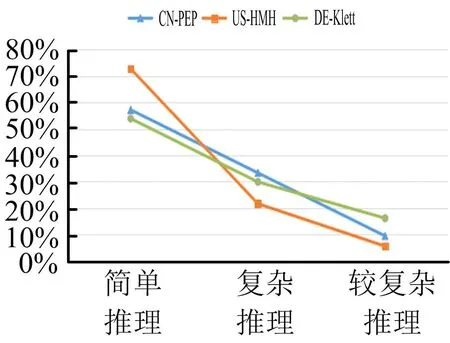
圖7 三種數(shù)學教材在習題運算因素上的比較

運算能力是數(shù)學能力的重要組成部分之一,通過數(shù)學運算,學生可以鞏固基本知識,提高解決實際問題的能力．通過圖7發(fā)現(xiàn),在“簡單運算”水平上,US-HMH版教材所占比例最多,其次是CN-PEP版,最后是DE-Klett版;在“復雜運算”水平上,CN-PEP版教材所占比例最多,其次是DE-Klett版,最后是,US-HMH版;在“較復雜運算”水平上,DE-Klett版所占比例多與CN-PEP版多與US-HMH版．

(4)知識含量

由表5可知,三種數(shù)學教材中,“1個知識點”的習題分別占57.14%、71.70%、52.99%,“2個知識點”的習題分別占28.57%、19.81%、30.77%,“3個知識點及以上”的習題分別占14.29%、8.49%、16.24%．繪制折線圖如圖8所示．

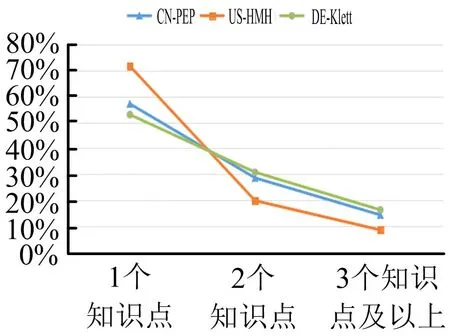
圖8 三種數(shù)學教材在知識含量因素上的比較

通過圖8發(fā)現(xiàn),在“1個知識點”水平上,US-HMH版教材所占比例最多,其次是CN-PEP版,最后是DE-Klett版;在“2個知識點”水平上,DE-Klett版教材所占比例最多,其次是CN-PEP版,最后是US-HMH版;在“3個知識點及以上”水平上,DE-Klett版所占比例多于CN-PEP版多于US-HMH版．通過對比發(fā)現(xiàn),US-HMH版教材偏重單個知識點的練習,DE-Klett版教材注重知識的綜合性練習．

(5)綜合難度

在對習題難度的4個因素進行比較分析的基礎上,根據(jù)習題綜合難度測量模型,對各難度因素進行加權平均值計算得到表6．

為了更加直觀呈現(xiàn)得到的結(jié)果,繪制雷達圖,如圖9．

圖9 三種數(shù)學教材習題綜合難度直觀模型

從“習題背景”上看,DE-Klett版大于CN-PEP版大于US-HMH版,從“推理水平”上CN-PEP版大于DE-Klett版大于US-HMH版,從“習題運算”和“知識含量”上看,DE-Klett版和US-HMH都大于CN-PEP版,最后從“綜合難度”上看,DE-Klett版大于CN-PEP版大于US-HMH版．

3 研究結(jié)論

三種版本數(shù)學教材“勾股定理”編寫既有相同之處,也有不同之處,相同之處表現(xiàn)在:

(1)在內(nèi)容選擇上,三種版本教材雖然標題或名稱不同,但都包括勾股定理,勾股定理逆定理基本知識點,在章節(jié)引入上,三種數(shù)學教材都使用了數(shù)學史素材．(2)在內(nèi)容組織上,三種版本教材都采用了“螺旋式”編寫特點,都注重數(shù)學內(nèi)容的整體性、聯(lián)系性.(3)在習題情境上,三個版本數(shù)學教材純數(shù)學情境所占比例最多,都重視注重問題情景和數(shù)學活動,提供大量的生活情境,強調(diào)數(shù)學與現(xiàn)實生活的關系．

三種版本數(shù)學教材“勾股定理”編寫存在著一定的差異,其差異性表現(xiàn)在:

(1)在內(nèi)容選擇上,美國版數(shù)學教材安排了“在平面直角坐標系中應用勾股定理”,其內(nèi)容廣度更廣．德國版數(shù)學教材涉及知識點比較廣,其內(nèi)容廣度更廣且內(nèi)容深度更深,例如安排了“在平面圖形和立體圖形中應該勾股定理”和“射影定理”等內(nèi)容．美國版教材和德國版教材都注重突出勾股定理的距離意義．

(2)在習題難度上,首先從“綜合難度”上看,德國數(shù)學教材習題難度最高,其次是人教版數(shù)學教材,最后是美國數(shù)學教材;從“習題背景”上看,德國數(shù)學教材大于人教版大于美國版;從“推理水平”上人教版數(shù)學教材大于德國數(shù)學教材大于美國數(shù)學教材;從“習題運算”和“知識含量”上看上,德國和美國數(shù)學教材都大于人教版數(shù)學教材．另外,值得一提的是美國版數(shù)學教材和德國版數(shù)學教材在教材最后都提供了練習題參考答案,人教版數(shù)學教材沒有習題參考答案．

4 啟示

它山之石可以攻玉,通過以上的分析,結(jié)合中國、美國、德國數(shù)學教材的特點,提出幾點對中國數(shù)學教材編寫的建議．

4.1 注重數(shù)學知識之間的聯(lián)系

通過比較分析發(fā)現(xiàn)三種版本數(shù)學教材都體現(xiàn)教材編寫的知識之間螺旋上升的特點,美國教材和德國教材在知識的內(nèi)容選擇上,內(nèi)容廣度更廣,內(nèi)容深度更深,尤其是德國數(shù)學教材,以“勾股定理”為例,把和“勾股定理”有關的知識點幾乎都聯(lián)系起來了．美國版教材和德國版教材都注重突出勾股定理的距離意義．教材編寫要體現(xiàn)知識之間的關聯(lián),將知識點按照一定的邏輯進行排序、整合,形成相互聯(lián)系、易于理解和遷移的知識結(jié)構,體現(xiàn)知識內(nèi)容的整體性和關聯(lián)性,體現(xiàn)大單元思想和知識的結(jié)構化特征．

4.2 注重真實問題情境的設置

PISA 2021把數(shù)學素養(yǎng)表述為:數(shù)學素養(yǎng)是個人在不同真實世界情境下進行數(shù)學推理并表示、使用和解釋數(shù)學來解決問題的能力[12]．三個版本教材都使用了大量的情境,都體現(xiàn)了數(shù)學與現(xiàn)實生活的聯(lián)系,以德國數(shù)學教材為例,不僅提供了大量的生活情境而且提供了一些科學情境,且教材情境圖片選擇真實、精美,與學生生活息息相關．在教材編寫過程中應注重真實情境的設置,提高學生在真實復雜情境中解決問題的能力,進一步提高學生的數(shù)學核心素養(yǎng)．

4.3 注重與信息技術的結(jié)合

信息技術最重要的價值之一就是變革數(shù)學教學模式,使得數(shù)學探究、數(shù)學實驗和數(shù)學建模等更加可操作[13]．以圖形計算器為例,信息技術支持下數(shù)學建模的教學不再局限于課堂,不再停留在虛擬的情境中．借助圖形計算器技術,學生可以直接在真實的生活情境和科學情境中收集數(shù)據(jù)、分析數(shù)據(jù)、構建模型并檢驗模型．在教材編寫時,不僅要體現(xiàn)計算工具的使用,也要體現(xiàn)圖形工具和軟件在數(shù)學中的應用,作圖軟件的應用可以更加直觀和精確地體現(xiàn)幾何圖形的特征,幫助學生增強學生的幾何直觀能力,發(fā)展學生空間想象能力和幾何邏輯推理證明能力,提高學生數(shù)學建模的能力．

4.4 注重與其他學科的融合

重視學科的交叉與融合,不僅是教育發(fā)展的必然趨勢,也是數(shù)學現(xiàn)代發(fā)展的時代特點,世界上許多國家都重視數(shù)學教科書中的跨學科內(nèi)容研究[14]．通過研究發(fā)現(xiàn)美國教材在習題設置上體現(xiàn)了STEM理念,專門設置了STEM題目．在教材編寫的過程中,體現(xiàn)跨學科的特征,不僅重視對自身學科的理解,也要注重學科之間的關聯(lián)和整合,以數(shù)學課程內(nèi)容為基礎,運用并整合其他學科知識,探究和解決社會生活和科學技術問題,提高學生應用數(shù)學的能力．