基于改進蟻群算法的醫藥冷鏈物流運輸路徑優化

陳鑫影,朱子青,胡明捷

(大連交通大學 計算機與通信工程學院,遼寧 大連 116028)

目前,我國醫藥冷鏈物流運輸仍處于初級發展階段,在基礎設施、冷鏈質量控制標準等方面存在較多不足,尚未形成完整的醫藥冷鏈物流體系[1],因此,有不少學者開始研究如何改變這種現狀。Qi等[2]以應急冷鏈物流資源調度最短時間為目標,構建了應急冷鏈物流調度模型。Zhang等[3]考慮到如何實現將綠色低能碳經濟產品物流與現代綠色冷鏈物流體系優化相結合,建立了模型。Xiong[4]考慮到傳統的算法優化方法搜索的時間長,提出一種改進蟻群優化算法。Liu等[5]以節約綜合經濟分析系統成本最低限度為系統設計主要目的,建立整數規劃模型。Zhang等[6]以配送成本最小、顧客滿意值最大為目標,進行求解。Ning等[7]根據其提出新的信息素平滑,增強信息素加強機制構建出新的蟻群算法。Luan等[8]將蟻群和遺傳算法融合,解決供應商選擇問題。Yue等[9]將懲罰策略融入蟻群算法,以解決無人汽車路徑規劃問題。Li等[10]將GA與TS算法相結合,解決了所提出的選址路由問題。Wang等[11]設計了一款基于啟發式規則的混合GA算法求解以最小成本為目標的函數。Zhu等[12]以再次生成停止進化粒子為目標,改進了粒子群算法。Ba等[13]在需求不定的緊急情況下建立了具有時間窗的物流配送模型。

以上研究在路徑優化模型方面取得了一定進展,但并沒考慮到預冷環節對總成本的影響,這在一定程度上影響了最優路徑的求解。為使總成本更加合理化,本文構建了醫藥冷鏈配送路徑優化模型,包括車輛的固定、運輸、懲罰、貨損、碳排放以及制冷成本,同時采用基于遺傳算法改進的蟻群優化算法(Improved Ant Colony Optimization Algorithm Based On Genetic Algorithm, IGACO)對該模型進行求解。由于IACO算法[4]存在收斂速度較慢以及易陷入局部最優的問題,本文在原算法基礎上加入輪盤賭規則、單點交叉操作、變異因子,保證IGACO可以搜索的范圍更廣、收斂速度更快,最后通過仿真試驗證明了IGACO算法的有效性。

1 模型約束條件

本文所提出醫藥冷鏈物流運輸路徑優化模型的問題描述如下:

(1)

(2)

(3)

(4)

(5)

其對應的約束條件為:

qi≥0,?i∈V

(6)

eti≤Ati≤lti,i∈n

(7)

eti-Ati>0, ?i∈V

(8)

lti-Ati<0, ?i∈V

(9)

式中:式(1)為車輛從配送點出發服務,完成后返回配送點;式(2)為每個用戶只可接受一個車的服務;式(3)為配送中心的車輛數有限,上限值為J;式(4)為路線客戶總需求小于車輛自身載重上限;式(5)為決策變量,值為0或1;式(6)為客戶需求量不得為負;式(7)為時間窗要求;式(8) 、式(9)為車輛或早或晚到達配送地。

2 數學模型的建立

在追求低碳大環境下,本文不僅將碳排放考慮進模型中,同時還將所需使用制冷劑的每個環節細化,從而構成改進后的制冷成本,以下為改進后的冷鏈配送路徑模型組成。

2.1 固定成本

固定成本費用包括但卻不僅僅局限在司機工資、車輛的磨損、折舊費等,因此固定成本C1可定義為:

(10)

2.2 運輸成本

運輸成本指車輛在實際配送服務過程中所產生的所有相關費用,包括但不局限于行駛中產生的燃油消耗以及車輛維修費用等,因此運輸成本C2可定義為:

(11)

式中:Wc代表每單位重量運費價格;dij為客戶i到j的距離;qi為客戶需求量。

2.3 懲罰成本

懲罰成本隨客戶的滿意度呈線性變化,同時滿意度被定義為配送車輛響應客戶需求所需時間的度量,若在客戶期望時間中,滿意度則為最高。客戶的期望時間周期為[eti,lti],且每個客戶都有自己單獨的時間窗要求,因此懲罰成本C3可定義為:

(12)

式中:Ati表示車輛配送到達時間;n為客戶數量,配送的客戶滿意度總值設為100;ε1、ε2代表早到、晚到對時間的窗敏感度。

2.4 碳排放成本

冷鏈配送車輛所產生的碳排放主要包括兩個方面,首先是車輛行駛過程中燃油消耗所產生的碳排放,其次就是車輛的制冷設備所產生的碳排放。車輛的燃油消耗所產生的碳排放量與車輛自身裝載重量以及配送距離的遠近相關。當車輛裝載量為X時,燃油消耗由e(X)表示,因此e(X)可表示為:

(13)

式中:Q為車輛滿載重量;e*為滿載時燃油消耗量;e0為空載時燃油消耗量。

有裝載的配送車在行駛過程中所產生的碳排放量,E1可表示為:

(14)

式中:CA為二氧化碳排放系數;dij為行駛距離;vij為車輛從i到j的行駛速度。

制冷設備所產生的碳排放量E2與載重、車輛行駛距離也有密切關系,可表示為:

(15)

式中:F為制冷設備所產生的碳排放。因此,總碳排放成本C4可表示為:

(16)

式中:c0為每單位碳稅價格。

2.5 貨損成本

貨損成本主要包含以下幾個部分:在裝載貨物之前,應當將制冷設備進行預冷,以達到提前降低貨艙溫度的目的,從而降低貨物因過高溫度而導致的損壞。同時,設備預冷時間、卸載貨物時間與貨損成本有直接關系,本文設置一個腐敗率函數:

R(t)=R0K-θt

(17)

式中:R0為貨物初始狀態時的質量;t為車輛配送貨物所需要的時間;θ為貨物質量對溫度的敏感系數;K為產品在某個衡定溫度下變質的常規速率。因此,貨損成本可表示為:

(18)

式中:t0表示的是車輛出發時的時間點;t1為車輛到達目的地的時間點;θ為進行預冷后貨物質量對溫度的敏感系數;θ1為卸貨過程中貨物對溫度的敏感系數;q1為每件貨物的單價;tj為卸貨時間。

2.6 制冷成本

制冷成本是冷鏈配送過程中配送車輛消耗制冷劑的成本,包括車輛提前預冷以及配送過程中制冷所產生的制冷劑消耗的費用總和。預冷操作時產生的制冷費用C61、運輸過程中固定產生的制冷費用C62以及卸貨過程中產生的制冷費用C63可表示為:

(19)

(20)

(21)

(22)

(23)

(24)

C6=C61+C62+C63

(25)

綜上所述,冷鏈物流配送優化路徑的總成本目標函數可表示為:

Z=Min(C1+C2+C3+C4+C5+C6)

(26)

3 基于遺傳算法改進的蟻群優化算法(IGACO)

本文將Xiong等[4]所提出的IACO算法中的啟發式因子放置于ACO算法中,并與遺傳算法相結合,使用改進后的ACO算法作為基礎解,在此基礎上進行單點交叉算子的操作,并將輪盤賭策略加入其中,這種方式可以擴大搜索范圍,從而達到篩選出不同適應度值的解,最后對適應度較低的解集,進一步進行變異操作,直到所有解集都達到理想的適應度值。通過遺傳算法的獨有特性,進而提高改進蟻群算法全局搜索能力,從而有效避免了過早陷入局部搜索最優化,同時進一步加快了算法全局的搜索收斂速度。

3.1 交叉變異策略

采取交叉操作有助于將優良的染色體傳給下一代,同時起到全局搜索作用,減少局部最優可能,例如將來自兩條不同的組合在隨機選擇位置進行分割,并交換右側部分的元素,從而得到全新的組合,見圖1。

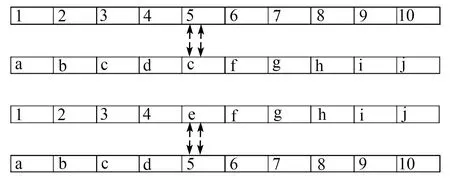
圖1 單點交叉演示圖

采取變異操作對算法尋優與算法進化有著非常重要的作用,若當算法陷入局部最優時,采取變異的操作,可以跳出局部的最優算法時,變異的操作則是直接將染色體序列中的某一部分進行隨機變異,對適應度較高的地區加強搜索,同時對適應度較低的部分繼續進行變異操作,直到達到給定的適應度閾值,從而終止變異操作。此操作在一定程度上增加了選擇的可能性,從而進一步防止算法過早陷入局部最優狀態,同時提高了算法的收斂度。

在信息素更新策略中,加入一個不斷變化的隨機函數q*,該參數將在給定的迭代范圍內隨機變化,從而增加選擇多樣性。基于以上策略,蟻群算法信息素濃度更新將更改為:

(27)

(28)

(29)

啟發式因子為:

用戶檢索后，進入二級目錄，網頁左側為數據庫分類，右側為該數據庫中包含的檢索結果，此種設計可提高用戶的檢索效率，如圖3所示。

(30)

式中:Li為螞蟻已經到達i點的距離總長;dij為地點i到地點j的距離;djp為將來走過各點之間的距離。

綜上所述,基于遺傳算法改進的蟻群算法可表示為:

(31)

3.2 IGACO算法流程

IGACO算法具體操作步驟如下:

步驟一:對算法初始解進行構建,并將此解作為算法初始解集。

步驟二:對初始解進行適應度值的求解,并根據適應度設置范圍篩選適應度較高的解。

步驟三:對信息素值進行更新,同時定義信息素矩陣,將矩陣中的信息素進行更新,并更新解向量,最后判斷是否達到算法設定迭代次數,若沒達到,返回步驟二,若達到則進行下一步。

步驟四:將信息素矩陣進行輸出,并進行交叉、變異操作。進行完交叉、變異后對矩陣進行拆解,最后判斷是否滿足算法終止條件,若滿足則輸出最優解,若不滿足則繼續進行此步驟。

圖2 IGACO算法流程圖

4 試驗設置與分析

本文分析了IGACO算法解決改進冷鏈模型的性能。IGACO的相關試驗參數設置:螞蟻數量為30只,迭代次數為500次,信息素蒸發量設置為0.2,信息素強度設置為l×108,交叉概率設置為0.8,變異概率設置為0.1。

改進模型參數見表1。

表1 模型相關的參數

4.1 收斂度對比

使用本文所提出的IGACO算法與現有的IACO算法、ACO算法、GA算法做試驗對比,從對比結果可以看出IGACO算法的收斂速度更快,可以看出IGACO相對其他算法更具優勢,算法收斂度對比如圖3所示。可知,IGACO算法迭代數為在187次時,就已經達到最優狀態,而IACO算法、ACO算法、GA算法迭代數分別于第249、385、439次時才達到最優狀態。

圖3 算法收斂度對比

4.2 行走路徑對比

本文通過四種算法,對試驗數據集進行求解,并繪制車輛配送路線圖見圖4～圖7,可知IGACO算法配送路線所用成本相較于其余3種算法更低。

圖4 IGACO算法路徑圖

圖4試驗共使用9輛車,對30個收貨點進行產品配送,驗證配送所用成本。每輛車配送路線分別為:0→19→10→29→0,0→13→21→5→22→0,0→15→20→9→0,0→4→24→26→7→0,0→16→23→28→27→0, 0→18→6→0, 0→1→3→23→0, 0→25→2→14→0,0→8→30→12→17→0。

圖5試驗共使用9輛車對30個收貨點進行產品配送,驗證配送所用成本。每輛車配送路線分別為: 0→18→11→17→22→0,0→10→2→19→0,0→16→9→0, 0→25→3→23→24→27→0, 0→26→24→1→30→12→0,0→13→21→15→0, 0→7→8→29→28→0,0→4→20→0,0→6→5→0。

圖5 IACO算法路徑圖

圖6試驗共使用9輛車對30個收貨點,進行產品配送,驗證配送所用成本。每輛車配送路線分別為:0→25→12→23→3→11→0,0→13→7→14→0,0→16→5→0, 0→17→1→10→29→0,0→21→15→0,0→28→8→0,0→2→24→4→20→23→0,0→18→27→26→22→0,0→19→9→6→0。

圖6 ACO算法路徑圖

圖7試驗共使用9輛車對30個收貨點進行產品配送,驗證配送所用成本。每輛車配送路線分別為:0→13→15→20→21→0,0→5→11→4→0,0→28→23→0,0→9→6→27→12→0,0→16→22→8→0,0→14→10→24→26→2→0,0→18→30→1→0,0→29→17→25→3→0,0→7→19→0。

以上 4 種算法中,IGACO、IACO、ACO、GA 算法求解模型總成本分別為 5 661.460 4、 5 940.018 5、6 636.764 5、 7 281.553 5 元。IGACO算法在總成本方面,較IACO、ACO、GA算法分別減少了4.9%、17.2%、28.6%。

4.3 運行時間對比

分別對IGACO算法、IACO算法、ACO算法、GA算法進行運行時間對比,每種算法均運行6次,對比結果見表2。

表2 4種算法運行時間對比 s

由表2可以看出, IGACO算法較ACO算法、GA算法、IACO算法分別提高了4.57、4.84、0.74 s,IGACO算法從運行時間上看是有提升的。

5 結論

本文對醫藥冷鏈物流運輸成本模型進行改進,在制冷成本中加入預冷參數,使制冷成本的組成因素更加合理化,同時提出的IGACO算法對傳統蟻群算法啟發式因子進行改進,并將解作為基礎解加上遺傳算法中的交叉操作以及變異因子,從而擴大算法搜索范圍,進一步避免算法陷入局部最優的可能。試驗發現,在運行速度、總成本計算、迭代次數方面,IGACO算法均優于其他幾種對比算法,具有較好的優越性和可靠性。

本文在某些方面考慮的并不是很充足,在今后工作中,冷鏈運輸模型參數可能會得到一定程度上的優化,隨著研究的繼續深入,新的算法模型或許也將考慮引進新的因子,以使算法效率進一步提升,本文沒有將多目標作為最終的求解目標,這將是下一個研究目標。