基于復雜振動載荷的高速列車齒輪箱體強度分析

尹曉亮,范軍,楊集友,曹磊,王明萌,趙曉丹,曾迎,張英波

(1.中車長春軌道客車股份有限公司,吉林 長春 130062;2.西南交通大學 材料先進技術教育部重點實驗室,四川 成都 610031)

傳動齒輪箱是軌道車輛走行部的重要零部件,其結(jié)構(gòu)振動特性和疲勞性能受到廣泛關注。隨著鐵路高速化和輕量化的發(fā)展,以及新一代CR450高速列車的投產(chǎn)與試運行,齒輪箱體承受的載荷條件變得更為復雜苛刻[1]。高速列車齒輪箱體不僅要承受電機扭矩載荷,還要承受輪軸傳遞的因線路激擾引起的振動載荷,由此導致的齒輪箱體失效將嚴重影響行車安全,故其安全性、可靠性、穩(wěn)定性對高速列車的安全運營至關重要[2]。目前國內(nèi)外對高速列車齒輪箱體的強度分析大多僅考慮電機的扭矩載荷[3-6],部分研究在分析箱體疲勞強度時雖然也考慮了振動載荷,但對工況組合進行了簡化,存在遺漏最危險條件的可能[7-8]。因此,本文在考慮振動載荷的基礎上[9-10],根據(jù)不同的工況組合對某車型高速列車齒輪箱體進行靜強度和疲勞強度分析,并對分析結(jié)果進行評定。

1 動力轉(zhuǎn)向架齒輪箱體結(jié)構(gòu)

本文齒輪箱采用一級圓柱漸開線斜齒輪傳動。齒輪箱體是由上箱體和下箱體組成的分體式結(jié)構(gòu),見圖1。齒輪箱體輸入端通過聯(lián)軸器與牽引電機連接,輸出端與車軸通過過盈方式連接。齒輪箱體的主要技術參數(shù)見表1。

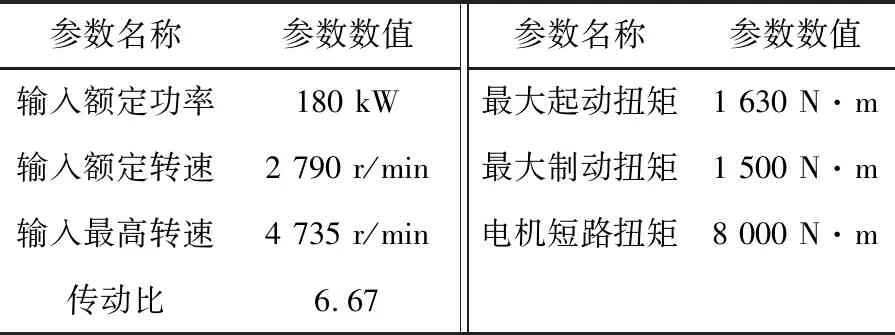
表1 齒輪箱體主要技術參數(shù)

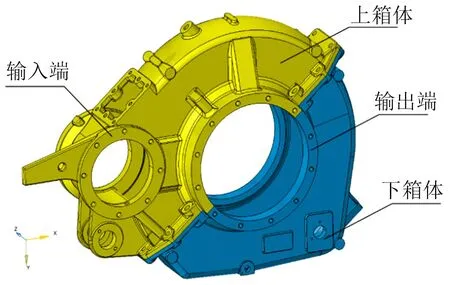
圖1 齒輪箱體結(jié)構(gòu)

2 齒輪箱體載荷工況及有限元模型

高速列車運行有牽引加速、惰力、制動減速和短路4種工況,在不同工況下齒輪箱體承受的載荷種類不同。

短路工況下齒輪箱體所受載荷為超常載荷,該載荷是一種在整個服役周期內(nèi)很少出現(xiàn)卻可能發(fā)生的極限載荷,齒輪箱體結(jié)構(gòu)必須能夠承受這種載荷的作用,且不發(fā)生永久變形。

在牽引加速、惰行和制動減速3種工況下齒輪箱體承受的載荷是正常運行條件下出現(xiàn)的運營載荷,要求齒輪箱體結(jié)構(gòu)在其設計壽命周期內(nèi)可承受這種載荷,且不發(fā)生疲勞失效。由于3種工況均為運營載荷,故可選擇其中最惡劣的一種工況進行疲勞強度校核。

齒輪箱體在動力傳遞系統(tǒng)中,既要承受牽引和制動工況下的扭矩作用,又要承受來自輪軸傳遞的線路激擾作用,參照BS EN 13749: 2021中D.2.3對齒輪箱體技術參數(shù)的要求[11],可確定齒輪箱體的超常振動載荷和正常運營振動載荷,見表2。

表2 振動載荷參數(shù)

高速列車正常運行時,齒輪箱體承受的不同方向線路激擾(載荷)是隨機組合出現(xiàn)的,為保證靜強度及疲勞強度分析結(jié)果的可靠性,確定電機正轉(zhuǎn)和反轉(zhuǎn)短路扭矩時為最惡劣工況,在此工況下考慮縱向、橫向以及垂向載荷的16種組合工況進行分析,疲勞強度計算工況采用最大啟動扭矩和最大制動扭矩中較大值進行考核,見表3、表4。

表3 靜強度計算載荷工況

表4 疲勞強度計算載荷工況

本文在Ansys平臺上建立了齒輪箱體的有限元模型。上下齒輪箱體結(jié)構(gòu)有限元模型見圖2。整個齒輪箱體強度分析的有限元模型由306 645個節(jié)點、1 399 886個四節(jié)點四面體單元Solid92、12個Beam單元、2個質(zhì)量單元和6 335個接觸對單元組成。

圖2 齒輪箱體結(jié)構(gòu)有限元模型

為了準確模擬齒輪箱體在轉(zhuǎn)向架運行過程中的受力狀態(tài),在齒輪箱體結(jié)構(gòu)有限元模型中,齒輪箱體與端蓋的結(jié)合面、滾動軸承與齒輪箱體和端蓋的結(jié)合面、螺栓頭部與齒輪箱體和端蓋的結(jié)合面、齒輪軸與齒輪箱體的接觸面均用接觸對模擬,而簡化模型的質(zhì)量用質(zhì)量單元進行模擬。

3 齒輪箱體靜強度分析

3.1 靜強度評定方法

齒輪箱體選用材料為球墨鑄鐵QT400-18L,其機械性能如下:抗拉強度σb為400 MPa;屈服強度σ0.2為230 MPa;彈性模量E為169 GPa;泊松比μ為0.275;密度為7.3 g/cm3。

根據(jù)UIC 615-1: 2003,齒輪箱體結(jié)構(gòu)在最大超常載荷作用下,其靜強度條件為結(jié)構(gòu)的最大Von_Mises應力不大于材料的彈性屈服極限,即:σVon_Mises≤σ0.2

3.2 計算結(jié)果與分析

對表3中的16種工況分別進行計算。每種工況下齒輪箱體的最大Von_Mises應力和安全系數(shù)見表5。在所有工況下,齒輪箱體在工況4時所產(chǎn)生的應力最大,為196.68 MPa,應力最大值出現(xiàn)在上箱體齒面觀察窗附近,其安全系數(shù)為1.17,應力分布見圖3、圖4。各工況下的應力值均小于材料的彈性屈服極限230 MPa,故箱體的靜強度滿足要求。

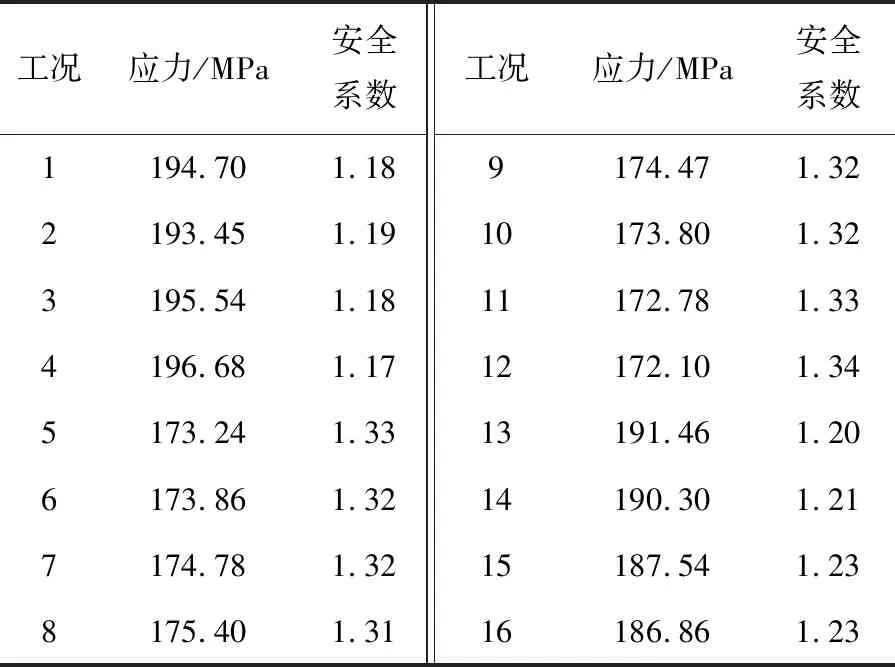
表5 不同工況齒輪箱體Von_Mises應力和安全系數(shù)

圖3 載荷工況4齒輪箱上箱體的Von_Mises應力分布

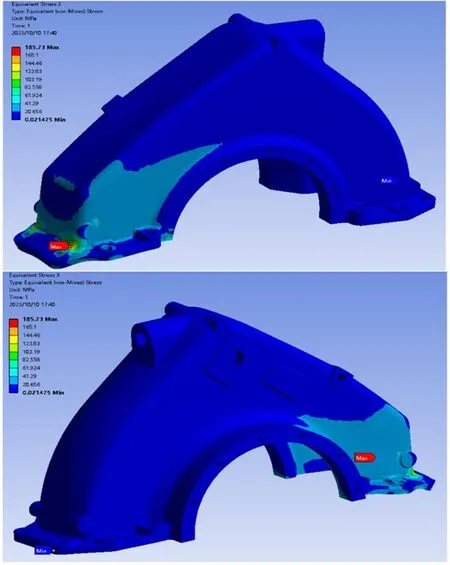
圖4 載荷工況4齒輪箱下箱體的Von_Mises應力分布

由表5中結(jié)果可知,齒輪箱體在不同載荷工況所產(chǎn)生的最大應力值不同,對應的位置也不同。在電機短路扭矩載荷不變的情況下,施加不同組合的載荷,對齒輪箱體的最大應力值有一定的影響。

4 齒輪箱體疲勞強度分析

4.1 疲勞強度評定方法

本文根據(jù)ERRI B12/RP17所提供的疲勞強度分析方法,對齒輪箱體結(jié)構(gòu)進行疲勞強度計算。在有限元分析中,每個節(jié)點的平均應力和應力幅的計算式為:

σm=(σmax+σmin)/2

(1)

σa=(σmax-σmin)/2

(2)

式中:σmax為節(jié)點應力循環(huán)的最大等效主應力;σmin為節(jié)點應力循環(huán)的最小等效主應力。

用ERRI B12/RP17的投影法獲得σm和σa的值,確定所有工況載荷下每個節(jié)點的應力幅值,用Haigh形式的Goodman疲勞曲線評定齒輪箱體的疲勞強度[12]。

QT400-18L的光滑試棒對稱循環(huán)疲勞極限為σ-1s,由于實際結(jié)構(gòu)的幾何尺寸與形狀、表面粗糙度和質(zhì)量等級與光滑試棒存在差異,其結(jié)構(gòu)的疲勞極限與試棒的疲勞極限滿足:

(3)

式中:Kf為疲勞缺口系數(shù);CL為載荷類型因子;ε為尺寸系數(shù);β為表面狀態(tài)系數(shù);σ-1為光滑試棒的疲勞極限;σ-1k為缺口試棒的疲勞極限。

確定齒輪箱體材料的Goodman疲勞極限時,缺口試棒疲勞極限為122 MPa,CL=1.0,ε=0.9,β=0.8,則材料Haigh形式的Goodman疲勞曲線見圖5。

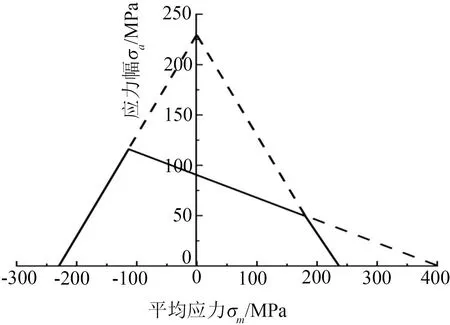
圖5 QT400-18L Haigh形式的Goodman曲線

4.2 計算結(jié)果與分析

在表4給出的載荷工況下,齒輪箱體節(jié)點應力幅與許用應力幅的比較見圖6。表6給出了齒輪箱體應力幅最大的10個節(jié)點的相關參數(shù)。從圖6和表6可以看出, 齒輪箱體應力幅值均小于其對應許用應力幅,最小安全系數(shù)為2.25,出現(xiàn)在259 940節(jié)點處。疲勞評估結(jié)果表明,齒輪箱體的疲勞強度滿足許用要求,說明齒輪箱體在設計壽命周期內(nèi),可承受牽引和制動工況下的扭矩載荷及線路激擾產(chǎn)生的振動載荷,且不發(fā)生疲勞失效。

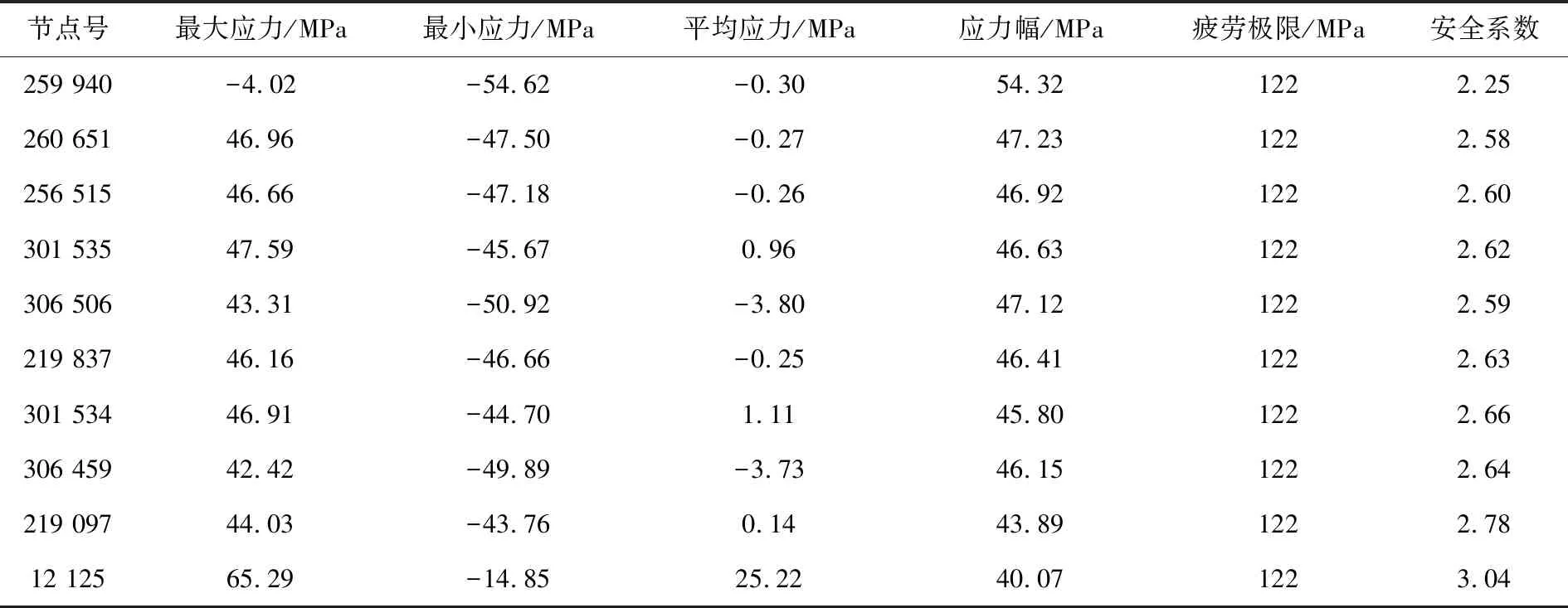
表6 應力幅最大的10個節(jié)點的相關參數(shù)

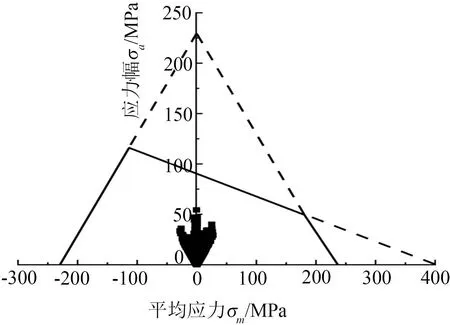
圖6 齒輪箱體節(jié)點的應力幅與許用應力幅比較

5 結(jié)論

本文對軸懸式齒輪箱體的16種載荷工況進行了靜強度和疲勞強度分析,分析結(jié)果如下:

(1) 在靜強度載荷工況下,當短路扭矩為8 000 N·m時,對齒輪箱體的局部應力進行校核驗證。齒輪箱體的最大應力(196.68 MPa)出現(xiàn)在齒輪箱上箱體齒面觀察窗附近,其最小安全系數(shù)為1.17,靜強度滿足許用要求。

(2) 在復雜運行載荷工況下,應力幅值均小于其對應許用應力幅,齒輪箱體的疲勞強度滿足許用要求。

(3) 疲勞強度評估結(jié)果表明,齒輪箱體在設計壽命周期內(nèi),可同時承受牽引/制動工況下的扭矩載荷及電機短路扭矩工況產(chǎn)生的振動載荷,且不發(fā)生疲勞失效。