面向聯邦學習激勵優化的演化博弈模型

孫躍杰,趙國生,廖祎瑋

(哈爾濱師范大學 計算機科學與信息工程學院,哈爾濱 150025)

0 引 言

深度學習技術蓬勃發展至今,能否獲取足夠的高質量樣本數據是制約其發展速度的重要因素之一.由于數據安全、競爭關系等因素,獲取數據過程中出現了嚴重的數據孤島問題,并且在數據的集中過程中還存在數據泄漏的風險.因此聯邦學習(Federated Learning,FL)作為新興的分布式機器學習范式應運而生[1].它使得各個參與方可以在不泄露底層數據的前提下共同建立模型,適用于訓練數據涉及敏感信息以及數據量過大無法集中收集的情況.然而,當客戶參與聯邦學習時,會不可避免的消耗他們的設備資源,同時客戶也承擔著一定的安全風險,因此對聯邦學習激勵機制的研究一直是當下的熱點.

區別于博弈論的一次直接達到納什均衡,演化博弈論的行為主體在演化過程中會動態修正自己的行為,在多次博弈之后達到均衡.據此而建立的聯邦學習激勵機制更切合實際并且更加有助于聯邦的長期穩定發展.

本文將演化博弈中的“適者生存”的基本思想運用到聯邦學習當中,將演化穩定策略(Evolutionary Stabilization Strategies,ESS)與復制動態方程(Copy Dynamic Equations,CDE)相結合,提出了一種演化均衡的聯邦學習激勵機制(Evolutionary Balanced Federated Learning Incentive Mechanism,EBFLIM).本文的主要貢獻如下:

1)通過模型質量評估算法評估聯邦參與者提交模型的質量同時量化其訓練成本,并對低質量模型提交進行篩除,以提升聯邦任務的完成效果.

2)提出了一種演化均衡的聯邦學習激勵機制EBFLIM,克服了聯邦學習中參與者虛報訓練成本造成的激勵不匹配問題,實現了對聯邦學習激勵機制的優化.

本文其余部分組織如下:第1節總結與聯邦學習激勵機制和演化博弈論相關的研究工作;第2節提出面向聯邦學習激勵優化的演化博弈模型;第3節針對本文提出的優化方法進行仿真實驗;第4對本文進行總結并交代下一步工作.

1 相關工作

1.1 聯邦激勵機制

為了聯邦激勵能夠更合理的覆蓋參與者的資源消耗,吸引更多高質量數據用戶加入聯邦,已有很多學者投入了聯邦學習激勵機制的研究.Tang等人[2]針對組織異質性和公共產品特性提出了社會福利最大化問題,并提出了一種針對cross-silo FL的激勵機制,同時提出了一種分布式算法,使組織能夠在不知道彼此的估值和成本的情況下最大化社會福利.Yu等人[3]為了解決訓練成本和激勵之間暫時不匹配的問題,提出了聯邦激勵機制,通過上下文感知的方式將給定的預算進行動態劃分,最大化集體效用,同時最小化數據所有者之間的不平等.Ding等人[4]針對non-IID數據進行了最優契約設計.契約規定了每一個類型用戶參與聯邦學習能夠獲得的獎勵并且會給到服務器更偏好的用戶類型更高的獎勵,從而達到激勵相對高效、低成本用戶參與聯邦學習的目的.Bai等人[5]首先構建眾包系統的激勵模型.其次,結合反向拍賣和VCG拍賣的概念,提出了一種基于拍賣的激勵機制.Sun等人[6]首先考慮了空地網絡的動態數字孿生和聯合學習,其次基于 Stackelberg 博弈設計聯邦學習的激勵機制.此外,考慮到不同的數字孿生偏差和網絡動態,設計了一個動態激勵方案,以自適應地調整最佳客戶的選擇及其參與程度.Richardson等人[7]考慮聯邦參與者因冗余數據獲得獎勵的搭便車現象,提出了基于影響力的激勵方案保證激勵預算與聯邦模型價值成比例有界,防止聯邦被迫支付多余獎勵.杜等人[8]提出了以在線雙邊拍賣機制為基礎的ODAM-DS算法.基于最優停止理論,幫助邊緣服務器在適當的時間選擇移動設備,最小化移動設備的平均能耗.Hu等人[9]首先,將數據質量和數據量相結合,構建了特定指標下的聯邦學習激勵機制模型.然后,對基于服務器平臺和數據島的效用函數構建的激勵機制模型進行了兩階段的Stackelberg博弈分析.最后,導出兩階段博弈的最優均衡解,確定平臺服務器和數據島的最優策略.從等人[10,11]建立了一個關于FL激勵機制設計的推理研究框架,提出了FML激勵機制設計問題的精確定義,基于不同的設置和目標提供了一個清單,供實踐者在沒有深入博弈論知識的情況下選擇合適的激勵機制.同時在文獻[11]中基于VCG 提出了一種聯邦激勵機制,使社會剩余最大化,并使聯邦的不公平最小化.

1.2 演化博弈論

博弈論作為解決雙方或多方收益問題的重要手段應用于各種環境,基于博弈論的聯邦學習激勵機制的研究近年來也非常火熱.Hasan等人[12]使用享樂博弈將聯邦的交互建模為穩定的聯盟劃分問題.解決了是否存在確保納什穩定聯盟分區的享樂博弈的問題,并分析了納什穩定集的非空條件.丁等人[13]針對以數據為中心的開放信息系統,基于演化博弈構建了面向隱私保護的多參與者訪問控制演化博弈模型.Byde等人[14]描述了一種基于演化的評估拍賣機制的方法,并將其應用于包括標準第一價格和第二價格密封投標拍賣在內的機制空間,對拍賣理論進行了擴展.王等人[15]介紹并給出了混合均勻有限人口中隨機演化動力學問題與確定復制方程的相互轉化關系.同時介紹了無標度、小世界等復雜網絡上演化博弈的研究結論.全等人[16]通過利用一個廣義適應度相關的Moran過程,研究了一個有限規模的良好混合種群中的對稱2×2博弈的演化模型,給出了博弈的進化穩定策略,并將其結果與無限種群中復制者動力學進行了比較.王等人[17]綜述了網絡群體行為和隨機演化博弈模型與分析方法等方面的研究工作.針對以上方面的若干研究方法進行總結,并探討了通過隨機演化博弈進行網絡群體行為研究的可行性.

由于聯邦參與者虛報成本而造成激勵不匹配的問題會導致集體利益受到損害,但現有的聯邦學習激勵機制缺乏對激勵不匹配問題的重視.

因此本文在考慮了信息不對稱因素的同時,構建演化博弈模型,設計了更符合實際應用場景的聯邦學習激勵機制.

2 面向聯邦學習激勵優化的演化博弈模型

本節提出一種面向聯邦學習激勵優化的演化博弈模型.首先在聯邦學習系統中建立聯邦參與者-聯邦組織者演化博弈模型(Federal Participant-Federal Organizer Evolutionary Game Model,FPFOEGM),然后通過對聯邦參與者提交的模型進行質量評估來過濾低質量模型,同時結合聯邦參與者的信譽度指標設計聯邦激勵策略,最后通過求解復制動態方程得到演化穩定策略.

2.1 模型假設

基于客戶-服務器架構構建的聯邦學習系統模型如圖1所示.考慮當前有n個聯邦參與者表示為P={p1,p2,…,pn}.有模型使用者向聯邦發送任務請求并將自己獲得收益的一部分下發給聯邦用于激勵聯邦參與者.為了能夠對模型進行質量評估和篩選,同時量化參與者訓練成本,在聯邦中加入具有一定計算能力的聯邦組織者,組織者接收參與者提交的模型進行篩選后將符合條件的模型上傳至參數服務器進行整合,并作為協調方在激勵預算允許的范圍內對參與者進行激勵.

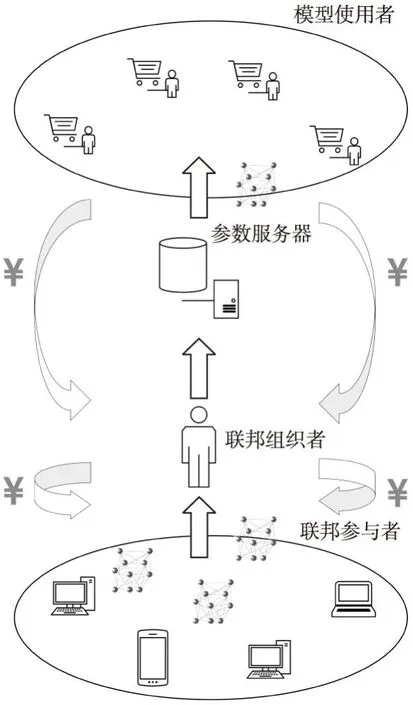
圖1 基于客戶-服務器架構的聯邦學習模型Fig.1 Federated learning model based on client-server architecture

本文在FPFOEGM模型中設置以下假設條件:

1)博弈參與者均具有有限理性.聯邦參與者通過選擇合適的模型提交策略獲得收益;聯邦組織者通過選擇適當的激勵策略獲得收益.

2)博弈雙方的策略選擇隨著博弈進行發生動態變化.

3)聯邦組織者的博弈收益即為聯邦的收益.

2.2 模型構建

FPFOEGM模型可以用一個三元組進行表示,FPFOEGM={M,S,U}.

1)M=(Np,No)表示演化博弈參與者,Np為聯邦參與者,No為聯邦組織者.

2)S=(Sp,So)表示聯邦參與者和聯邦組織者的策略空間,其中Sp={Sp1,Sp2,…,Spn}為聯邦參與者的策略集,So={So1,So2,…,Som}為聯邦組織者的策略集.

3)U=(Up,Uo)表示博弈雙方收益函數集合,Up為聯邦參與者的收益函數,Uo為聯邦組織者的收益函數.

在演化博弈模型中,聯邦參與者和聯邦組織者均有多個博弈策略可選擇,并且雙方選擇同一個策略的概率會隨著博弈進行發生變化,因此雙方的策略選取是一個動態過程.

2.3 基于演化博弈的聯邦學習激勵優化方法

本節對聯邦參與者提交模型的質量進行了評估并且針對聯邦中的成本虛報現象設定信譽度指標.提出了一種基于演化博弈的聯邦學習激勵優化方法.

2.3.1 模型質量評估

將模型質量評估加入FPFOEGM模型,量化模型訓練成本的同時去除低質量的模型提交.當聯邦參與者接收到來自模型使用者發布的任務時,將從參數服務器中下載模型數據并使用本地數據進行訓練,提交訓練好的模型表示為M={m1,m2,…,mn},有m個評估模型質量的指標A={a1,a2,…,am},G=gij表示聯邦參與者提交的訓練模型mi在指標aj上的評估值.模型質量的評估與測試集的測試結果密切相關,因此基于混淆矩陣將模型質量評價指標總結為準確率(a1)、精確率(a2)、召回率(a3)3種.

由于以上評估指標均與模型質量成正相關,因此可以通過式(1)對指標進行歸一化處理,并以此為依據去除低質量模型.

(1)

(2)

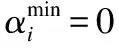
針對模型使用者對模型性能的不同需求,引入權重ωj,使模型質量評估結果更加符合實際情況.通過式(3)對參與者pi第k次提交模型的質量進行評估,便于聯邦組織者進行激勵策略選擇.

(3)

模型質量評估算法如表1所示.

表1 模型質量評估算法Table 1 Model quality assessment algorithm

2.3.2 信譽度評估

在聯邦學習中,每個參與者追求個體利益最大化時,存在虛報訓練成本的情況,即上報聯邦的成本與提交模型的質量不匹配,這會導致集體利益受到損害甚至造成合作失敗.因此在對聯邦參與者提交的模型進行質量評估后,針對虛報成本現象進行信譽度評估.

一般情況下,聯邦學習中的聯邦參與者的訓練成本與其提交的模型質量成正比,因此本文假設其真實訓練成本與模型質量在數值上相等.在聯邦學習中,聯邦參與者上報的成本超出真實成本越多,其信譽度越低,反之信譽度則越高.

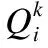
(4)

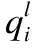
(5)

(6)

表2 信譽度評估算法Table 2 Reputation evaluation algorithms

2.3.3 激勵分配方法

在對聯邦參與者提交模型的質量及其信譽度進行評估的基礎上,設計激勵策略削弱聯邦參與者虛報訓練成本的欲望提高聯邦整體效用.

(7)

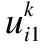
(8)

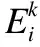
(9)

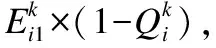
(10)

(11)

綜上可得:

(12)

激勵分配算法如表3所示.

表3 激勵分配算法Table 3 Incentive allocation algorithm

2.4 收益矩陣分析

在FPFOEGM中,考慮到聯邦參與者虛報訓練成本的情況引入了聯邦組織者,聯邦參與者為P,聯邦組織者為O.構建聯邦參與者的策略集{PS1,PS2},PS1表示誠實即上報成本等于真實訓練成本、PS2表示虛報,即上報成本大于真實訓練成本;構建聯邦組織者的策略集{OS1,OS2},OS1表示使用模型,OS2表示不使用模型.一般情況下,聯邦給予聯邦參與者的激勵可以覆蓋其訓練成本.

下面分析博弈過程中參與者的收益情況,參與者在不同策略下的收益情況如表4所示.

表4 參與者和組織者的收益矩陣Table 4 Benefit matrix of participants and organizers

其中c1、c2分別為聯邦參與者選擇誠實策略和虛報策略時,其真實訓練成本.s為來自聯邦的激勵收益,e1、e2為聯邦使用模型獲得的收益.

基于上述收益矩陣,設x為P中采用策略PS1的參與者所占比例,y為O中采用策略OS1的組織者所占比例.則聯邦參與者如實上報成本和虛報成本下的期望收益如式(13)所示:

(13)

聯邦參與者的平均收益如式(14)所示:

(14)

由此可得聯邦參與者的復制動態方程如式(15)所示:

(15)

同理,聯邦組織者使用模型和不使用模型的期望收益如式(16)所示:

(16)

聯邦組織者的平均收益如式(17)所示:

(17)

則聯邦組織者的復制動態方程如式(18)所示:

(18)

2.5 演化穩定策略

基于聯邦參與者與聯邦組織者的復制動態方程,對EBFLIM模型的演化穩定策略的求解過程如下:

1)計算復制動態方程的穩定解

2)演化穩定性分析

①聯邦參與者上報成本策略的演化博弈分析

圖2 聯邦參與者復制動態相位圖Fig.2 Replication dynamic phase diagram of federated participants

②聯邦組織者策略的演化博弈分析

圖3 聯邦組織者復制動態相位圖Fig.3 Replication dynamic phase diagram of the federation organizer

③聯邦參與者與聯邦組織者的博弈演化穩定策略

演化穩定策略指如果絕大多數個體選擇演化穩定策略,那么小部分的突變個體就無法入侵到這個群體[18].根據上述演化穩定均衡解,構建雅可比矩陣,求出行列式與跡.雅可比矩陣構建如式(19)所示:

(19)

根據雅可比矩陣計算其行列式和跡,結果如式(20)和式(21)所示:

(20)

TrJ=(1-2x)[y(s1-s2)+(c2-c1)]+
(1-2y)[x(s2-s1+e1-e2)+(e2-s2)]

(21)

在EBFLIM模型中,選擇虛報策略的聯邦參與者的實際訓練成本較低,所以c1>c2在基于模型質量以及聯邦參與者信譽度的聯邦激勵機制的作用下,聯邦參與者和聯邦組織者的收益滿足以下條件:s1-c1>s2-c2,e1-s1>e2-s2.

利用雅可比矩陣判斷是否為演化穩定策略,若局部平衡點對應矩陣的行列式DerJ大于零,且跡TrJ小于零,則為ESS;若DerJ大于零,且跡TrJ大于零,則為不穩定解;若DerJ小于零,且跡TrJ為任意值,則為鞍點.

基于以上條件局部均衡點穩定性分析如表5所示.

表5 局部均衡點穩定性分析Table 5 Stability analysis of local equilibrium point

3 仿真實驗

3.1 仿真設置

本文使用經典MNIST手寫數據集進行實驗仿真.為了真實還原聯邦學習系統環境,將訓練圖例按照隨機比例分配給10名聯邦參與者以模擬參與者持有不同訓練資源的情形,并從中隨機選取5名有意虛報訓練成本的參與者.本實驗在Windows系統下通過Matlab平臺搭建GoogLeNet執行手寫數字識別訓練任務以模仿參與者訓練模型的過程.具體參數設置如表6所示.

表6 訓練參數設置Table 6 Training parameter setting

3.2 實驗結果分析

首先對參與者提交模型的質量及參與者信譽度進行評估,在EBFLIM中,聯邦參與者提交高質量的模型可以得到更多的激勵收益,同時也會提升聯邦的總體效用.10名聯邦參與者使用各自持有的數據對模型進行訓練,之后用相同的測試集對他們訓練好的模型進行測試,測試準確率如圖4所示.

圖4 測試準確率Fig.4 Test accuracy

通過對測試結果進一步分析可以得到10個模型對應的混淆矩陣,通過公式(22)計算Precision和Recall.

(22)

其中TP表示是正類并且被判定為正類的實例,FP表示實際為負類但被判定為正類的實例,FN表示本為正類但被判定為負類的實例.

每個模型識別不同類別測試樣例的精確率與召回率應被分以不同的權重,在仿真實驗過程中,為了簡化實驗過程,將不同分類的權重均設置為1,則進一步處理后,不同模型對應的精確率與召回率如圖5所示.

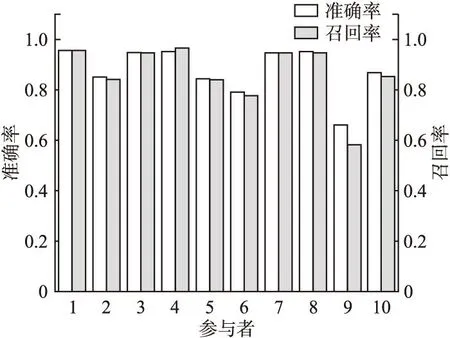
圖5 處理后的精確率與召回率Fig.5 Precision and recall after processing

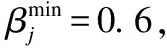
表7 參與者的模型質量、上報成本和信譽度Table 7 Model quality,reporting cost,and creditworthiness of participants

由表7數據可知,參與者9因未能通過模型質量篩選而被移出聯邦,在本實驗設置的條件下,對使用模型評估算法前后兩種狀態下的聯邦學習系統引入FedAvg框架[19]進行參數聚合得到兩個訓練模型,用相同測試集對兩個模型進行測試,輸出相應的混淆矩陣,測試結果表明,在參與者9持有數據占比僅為0.3%的情況下,經過模型質量篩選后聚合得到的模型的精度仍比未經過篩選得到的模型提高了0.01%.在聯邦學習實際應用的過程中,該方法對聯邦模型精度的提升效果會隨著數據量以及聯邦參與者數量的增加而更加顯著.

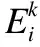
(23)

在個體收益分享法中,參與者i對集合體做出的邊際收益被用于計算他能得到的收益分成如式(24)所示:

(24)

其中v(X)表示評估集合體效用的函數.

使用3種不同的激勵分配方法,聯邦參與者的激勵收益情況如圖6所示.

圖6 不同分配方法下參與者的收益Fig.6 Benefits of participants under different distribution methods

EBFLIM在進行激勵分配時,綜合考慮了參與者虛報成本的現象,降低虛報參與者的激勵收益,同時提高誠實上報訓練成本的參與者的激勵收益.如圖6所示,利用平均分配法和個體收益分享法均會導致部分誠實上報訓練成本的參與者的收益占比小于或等于部分真實訓練成本較低的虛報者,而EBFLIM對虛報者的激勵收益進行了削減并將其二次分配給誠實上報成本的參與者,與平均分配法和個體收益分享法相比誠實參與者的收益提升了70%和57.4%,虛報參與者收益降低了65%和69.5%,達到了提高聯邦參與者積極性,減少虛報現象的目的.

進一步分析聯邦參與者與聯邦組織者的演化過程和模型中最優策略的選取問題.[x,y]初值分別取[0.2,0.8],[0.4,0.6],[0.6,0.4],[0.8,0.2],圖7展示了在激勵機制的作用下博弈雙方的動態演化的過程,可見不同初始狀態的策略選擇經過演化最終會達到一定的穩定狀態并且該狀態可以使參與者與聯邦均獲得最佳收益.

圖7 不同初始狀態的動態演化過程Fig.7 Dynamic evolution process of different initial states

4 結束語

本文提出了面向聯邦學習激勵優化的演化博弈模型,分析評價表明,優化后的聯邦學習激勵方法能夠有效的限制聯邦中虛報成本的參與者的收益,降低其虛報成本的動力,同時在不同初始情況下參與者與聯邦均能選取使雙方收益最優的策略,提高了聯邦的整體效益.下一步的工作首先是將其它導致聯邦學習激勵不匹配的因素融合進來,以適用于更多樣的情形.其次是嘗試對所提激勵優化方法進行應用.