縱向題目作答時間模型：對潛在加工速度的變化追蹤*

陳琦鵬 詹沛達，2，3**

（1.浙江師范大學心理學院，金華 321004；2.浙江省兒童青少年心理健康與危機干預智能實驗室，金華 321004；3.浙江省智能教育技術與應用重點實驗室，金華 321004）

1 引 言

在心理與教育研究中，研究者通常對個體或群體在特定時間跨度中的認知或行為的發展變化感興趣。這類研究的目標側重于刻畫每個個體的發展趨勢和群體的平均變化軌跡（劉紅云，孟慶茂，2003）。目前，針對不同的觀測變量類型和潛變量類型（連續或分類）研究者們提出了眾多縱向數據分析模型，比如縱向Rasch/IRT 模型（Andersen，1985；von Davier er al.，2011）、潛在增長曲線模型（Kaplan，2000）和潛在轉換分析模型（Collins & Lanza，2010）等。盡管縱向模型本身并沒有限制所分析的數據類型及所測量的潛在建構，但縱觀已有研究可發現幾乎所有縱向模型僅關注對傳統題目作答結果（response accuracy，RA）數據（e.g.，答對答錯或李克特式題目得分）的分析，忽略了其他模態數據，進而局限于追蹤RA 數據測量的心理建構（e.g.，潛在能力）的發展變化。

隨著計算機（網絡）化測評的普及，除傳統RA 數據外，對諸如題目作答時間（response time，RT）等過程數據的采集已越發普遍（韓雨婷等，2022；劉耀輝等，2022）。在心理與教育測評中，RT 數據作為一種RA數據的補充數據，描述了個體解決單一問題的總耗時，可用于分析個體解決問題時的潛在加工速度。這在一定程度上打破了傳統心理測量中對速度測驗和難度測驗的功能劃分。另外，因RT 數據“具有標準化數據結構，符合心理計量模型的建模與分析要求”（詹沛達，2022，p1417），近些年受到了研究者們的廣泛關注，開發了諸多RT模型（郭磊等，2017），比如對數正態RT 模型（lognormal RT model，LRTM）（van der Linden，2006；Klein Entink，Fox et al.，2009）。但縱觀已有研究可發現幾乎所有RT 模型都僅適用于分析橫斷測評數據，即僅能分析被試在單一時間點測驗中的潛在加工速度，無法追蹤個體潛在加工速度的發展軌跡。

目前，隨著計算機化測驗的普及，一些形成性學測項目已經可以便捷地采集每個時間點上個體對每道題目的RT 數據（即縱向RT 數 據）（e.g.，Wang & Nydick，2020；Wang，Zhang et al.，2018）。Wang 和Zhang等人（2018）發現在自適應學測系統中，隨著干預（反饋/ 學習）次數的增加，學生群體在下一個時間點上作答所有題目的平均RT 會呈現下降趨勢。Shi 等人（2018）發現在閱讀理解任務中借助智能導學系統能夠在一定程度上減少被試的RT。而上述例子中導致觀測變量RT 減少的一個主要可能原因是被試的潛在加工速度隨時間發生了提高。此時，如何合理分析縱向RT 數據以實現對潛在加工速度發展的客觀追蹤，是一個兼具理論與實踐意義的議題。

綜上所述，已有的縱向數據分析模型主要聚焦對縱向RA 數據的分析，少有研究關注縱向RT 數據的分析；且已有的RT模型多限于分析橫斷測評數據，無法追蹤學生潛在加工速度隨時間的發展。除聯合分析RA 和RT 數據外，單獨關注RT 數據的 分 析 也 很 常 見（e.g.，Guo et al.，2021；Klein Entink，van der Linden et al.，2009；van der Linden，2006；Wang，et al.，2013；詹沛達等，2020）。對此，本研究擬基于兩類常見的縱向數據分析方法（i.e.，多元正態分布建模和潛在增長曲線建模） 對最具代表性的LRTM 進行拓展，提出四個縱向RT 模型；以期實現對個體潛在加工速度發展的客觀追蹤并豐富縱向RT 數據的分析方法。對此，下文將按如下邏輯撰寫。首先，簡單回顧橫斷LRTM，并基于此提出四個縱向RT模型。其次，通過對一則有關空間旋轉能力的縱向RT 數據的分析，呈現新模型的實踐表現。然后，使用一則模擬研究去探究新提出的縱向RT 模型在不同模擬測驗條件下的表現。

1 縱向題目作答時間模型

在心理計量模型中，縱向模型的一個核心作用是描述不同時間點上被試潛在建構的變化關系。本研究關注兩類縱向建模方式：一類是基于多元正態分布的縱向模型（e.g.，Andersen，1985；Paek，Li，& Park，2016；von Davier et al.，2011；Zhan et al.，2019），另一類是基于潛在增長曲線的縱向模型（e.g.，Bollen & Curran，2006；Kaplan，2000；Wang & Nydick，2020）。前者類似于多維IRT 模型，直接利用多元正態分布對被試在各時間點上的潛在建構進行建模，并可利用均值向量描述不同時間點上群體的發展軌跡；后者通過構建潛在建構與測驗時間點之間的線性或非線性回歸函數來描述潛在建構隨時間點增加的變化趨勢。

基于上述兩種建模邏輯，本文提出兩類縱向RT 模型：基于多元正態分布的縱向RT 模型和潛在增長曲線的縱向RT 模型。上述兩類模型的差異在于描述各時間點上潛在構建關系的結構模型，而測量模型保持一致。因此，下文先介紹統一的測量模型，然后再結合不同的結構模型逐一闡述四個新模型。

1.1 測量模型

針對橫斷RT 數據，LRTM 是目前最常用的RT 測量模型之一。設定Tni為被試n（n=1，...，N）對 題 目i（i=1，...，I）的 作 答 時間。則LRTM 可表示為

或

其中，τn是被試n 的潛在加工速度；ξi為題目i 的時間強度參數，表示被試群體作答題目i 的平均耗時；?i為題目i 的時間區分度參數，反映潛在加工速度對觀察作答時間的影響程度；εni為殘差，ωi為題目i 的時間精度參數。

對于縱向測評而言，當整個測驗包含P 個測驗時間點，則第p 個時間點上縱向LRTM 的測量模型可表示為：

其中，Tnip是時間點p 上被試n 對題目i 的作答時間；ξip、φip和ωip分別是時間點p上題目i 的時間強度參數、時間區分度參數和時間精度參數；τnp是時間點p 上被試n 的潛在加工速度。

1.2 基于多元正態分布的縱向題目作答時間模型

為描述P 個時間點上τnp之間的關系，一種最直接的方法是構建多元正態分布，如圖1（a）。即假設τn=（τn1，…，τnP）T是遵循多元正態分布的多維潛在加工速度向量：

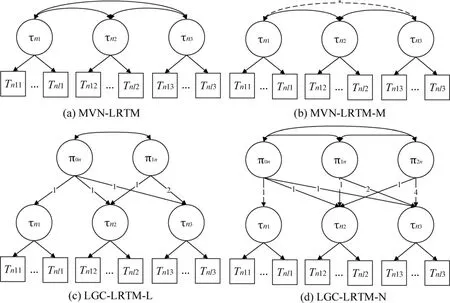
圖1 四個縱向題目作答時間模型示意圖（P=3）

式中，μ=（μ1，…，μP）T為P 個時間點的潛在加工速度的均值向量；Σ 為方差協方差矩陣，描述了P 個時間點的潛在加工速度之間的關系。該模型直接估計的各個時間點上的潛在加工速度，因此可直接使用＾τn描述被試個體潛在加工速度的發展軌跡。此時，可以用＾τn（p+1）-＾τnp描述相鄰時間點個體水平的變化程度，用＾μp+1-＾μp描述相鄰時間點群體均值的變化程度。

該模型可視為多維LRTM（詹沛達等，2020）在縱向RT 數據分析中的應用。與多維LRTM 一樣，該模型中的所有元素均需自由估計，即中有個待估計參數。該做法相對優點是考慮了所有時間點上潛在加工速度之間的相互影響，相對缺點是當時間點P 數量較多時參數估計計算量較大且易出現估計不收斂問題。

為縮減待估計參數數量，可通過引入馬爾可夫性質來約束中的待估計參數，如圖1（b）。目前已有許多研究將馬爾可夫性質引入縱向數據分析中（e.g.，de Haan-Rietdijk et al.，2017；Zhan，2020）。基于馬爾可夫性質，可假設被試在時間點p 的潛在加工速度只與其在時間點p-1 的潛在加工速度有直接關系。對此，將做如下轉換：

其中，S 為標準差矩陣，Ω 為相關系數矩陣。然后，因只考慮相鄰時間點之間的直接關系，所以只需將相關矩陣Ω 中相鄰時間點的相關系數ρ(p-1)p作為待估參數；而跨時間點的相關系數不視為待估計參數，由各相鄰時間點上的相關系數連乘而來：

其中，ρab為兩個不相鄰的兩個時間點a 和b 之間的相關系數，比如，ρ13=ρ12ρ23。此時，Σ中待估計參數數量由P（P+1）/2 縮減為2P-1。

為便于闡述，下文將不包含馬爾可夫性質的和包含馬爾可夫性質的模型分別簡稱為MVN-LRTM 和MVN-LRTM-M。另外，在采用錨題設計和重復測量設計的情況下，可將第一時間點上所有被試的潛在加工速度的均值和方差分別約束為μ1=0和σ2τ1=1 以保證模型的可識別性（Paek et al.，2016）。

1.3 基于潛在增長曲線的縱向題目作答時間模型

為描述P 個時間點上τnp之間的關系，多元正態分布外的另一種方法是構建潛在增長曲線，如圖1（c）：

①也有研究不考慮殘差項（e.g.，Curtis，2010），即τnp=π0n+π1n（p-1）；預研究結果表明不考慮殘差項的模型對實證數據的擬合結果較差.

式中，π0n為被試n 的截距系數，表示被試n的初始潛在加工速度水平；π1n為被試n 的增長系數，表示被試n 的潛在加工速度隨時間變化的程度；π0n和π1n服從二元正態分布，兩者的均值μ0n和μ1n分別代表群體潛在加工速度的均值和群體潛在加工速度的平均增長率，方差協方差矩陣則描述了潛在加工速度的初始水平和增長系數之間的關系：ρπ1π0＞0 意味著初始水平越高的被試，其潛在加工速度隨時間的增幅越大，反之則反；εnp為殘差。與MVN-LRTM 不同，該模型沒有直接估計各時間點上的τnp，而是估計了每個被試的增長曲線系數（i.e.，π0n和π1n）；此時，可以用＾π1n描述相鄰時間點個體水平的變化程度，用＾μπ1描述相鄰時間點群體均值的變化程度。

公式9 假設τnp隨測驗時間點的增加呈線性增長，而現實中τnp隨測驗時間點的增加也可能呈非線性增長。此時，可在公式9 中增加二次增長項來實現對潛在加工速度的非線性變化的描述，如圖1（d）：

式中，π2n為被試n 的二次增長系數，其余參數同上。

除包含二次增長項外，非線性增長模型中還可以進一步包含三次增長項或自由估計時間參數，限于篇幅限制本文暫不關注它們。為便于闡述，下文將基于線性增長曲線和基于非線性增長曲線的模型分別稱為LGC-LRTM-L 和LGC-LRTM-N。另外，在采用錨題設計和重復測量設計的情況下，可將第一時間點上所有被試的潛在加工速度的均值和方差分別約束為μπ0=0 和σ2π1+σ2ε1=1 以 保 證 模 型 的 可 識 別 性（e.g.，Wang&Nydick，2020）。

2 實證數據分析

2.1 數據描述與分析

本研究以一則有關空間旋轉能力的自適應學測數據（Wang，Yang et al.，2018）為例來展現所提出模型的實踐可應用性。該數據集包含350 名被試在5 個時間點上的作答數據，數據集的詳細描述信息可見附錄S1。圖2 呈現了題目的對數RT 隨時間變化趨勢（剔除缺失值），可發現明顯的下降趨勢。

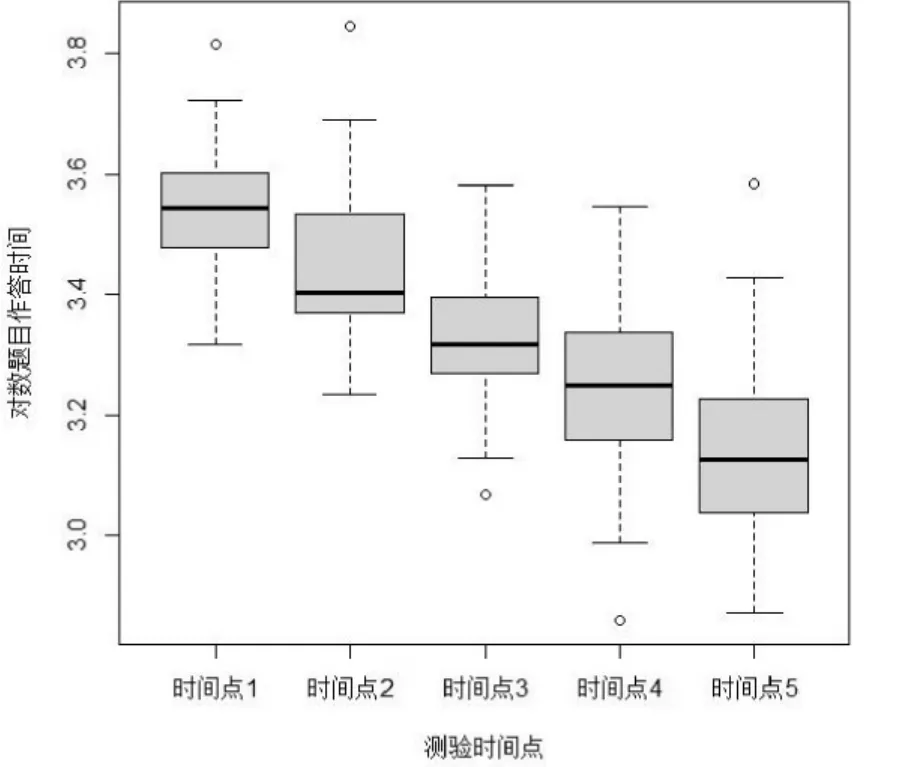
圖2 實證研究5 個時間點上50 道題目的對數題目作答時間分布

分別使用MVN-LRTM、MVN-LRTM-M、LGC-LRTM-L 和LGC-LRTM-N 作為數據分析模型。模型參數估計設定及不同信息量先驗下的穩健型分析可見附錄S2。使用潛在量尺縮減因子（PSRF；Brooks & Gelman，1998） 對作為MCMC 算法的收斂指標。使用后驗預測模型檢驗（PPMC）評估模型對數據的絕對擬合程度；在計算后驗預測概率（ppp）時較了觀察數據X 和后驗預測數據Xpostpred之間的差異：ppp=∑Ee=1（Sum（Xpostpred(e)）≥Sum（Y））/E ，其中E 為MCMC中的抽樣次數，Xpostpred(e)為第e 次抽樣中的后驗預測值，由公式3 計算得到。使用-2LL（-2×log likelihood）和DIC（Spiegelhalter et al.，2002）作為模型-數據相對擬合指標。有關擬合指標更多的信息可見附錄S3。

2.2 結果

需要強調的是，MVN-LRTM 中潛在加工速度的方差協方差矩陣中部分元素沒有達到收斂標準（PSRF＜1.2），表明模型參數估計值沒有穩定在一個特定值附近；在不收斂情況下得到的估計值（后驗均值），無法排除MCMC 隨機抽樣誤差的影響，難以反映數據本身所蘊含的特性；因此，該模型與數據的擬合結果僅供參考。其他三個模型的所有模型參數均達到收斂標準。

表1 呈現了四個模型對實證數據的擬合情況。首先，根據各時間點上的ppp 值，表明四個模型均擬合該數據。其次，不考慮MVN-LRTM 時，剩余三個模型的對數據的相對擬合比較接近。其中，-2LL 指標值表明，在不考慮模型復雜性懲罰的前提下，LGC-LRTM-N 對該數據的擬合相對最好，即該模型得到的參數估計值相對最能反映數據的特征。 而 DIC 指標值表明MVN-LRTM-M 對該數據擬合相對最好，LGC-LRTM-L 次之且和LGC-LRTM-N 幾乎沒有差異。總之，當考慮模型復雜性懲罰時，MVN-LRTM-M 對該數據擬合相對最好，而不考慮模型復雜性懲罰時，LGC-LRTM-N 的參數估計結果最能反映數據本身特征。

表1 實證研究中模型-數據擬合結果.

圖3 呈現了四個模型中所有被試潛在加工速度隨時間的變化趨勢（含群體均值變化）。對任何模型而言，潛在加工速度的群體均值都呈較明顯的增長趨勢。圖4 呈現了四個模型中所有時間點上潛在加工速度的估計值之間的相關系數圖。可以看到，無論是同一模型對5 個時間點上潛在加工速度的估計值之間，還是不同模型對同一時間點上潛在加工速度的估計值之間，均呈現高程度相關。一方面表明不同模型的估計值之間具有高度一致性，另一方面表明不同時間點上潛在加工速度之間也具有高度一致性（主要原因是該測驗中各時間點之間的間隔較短）。

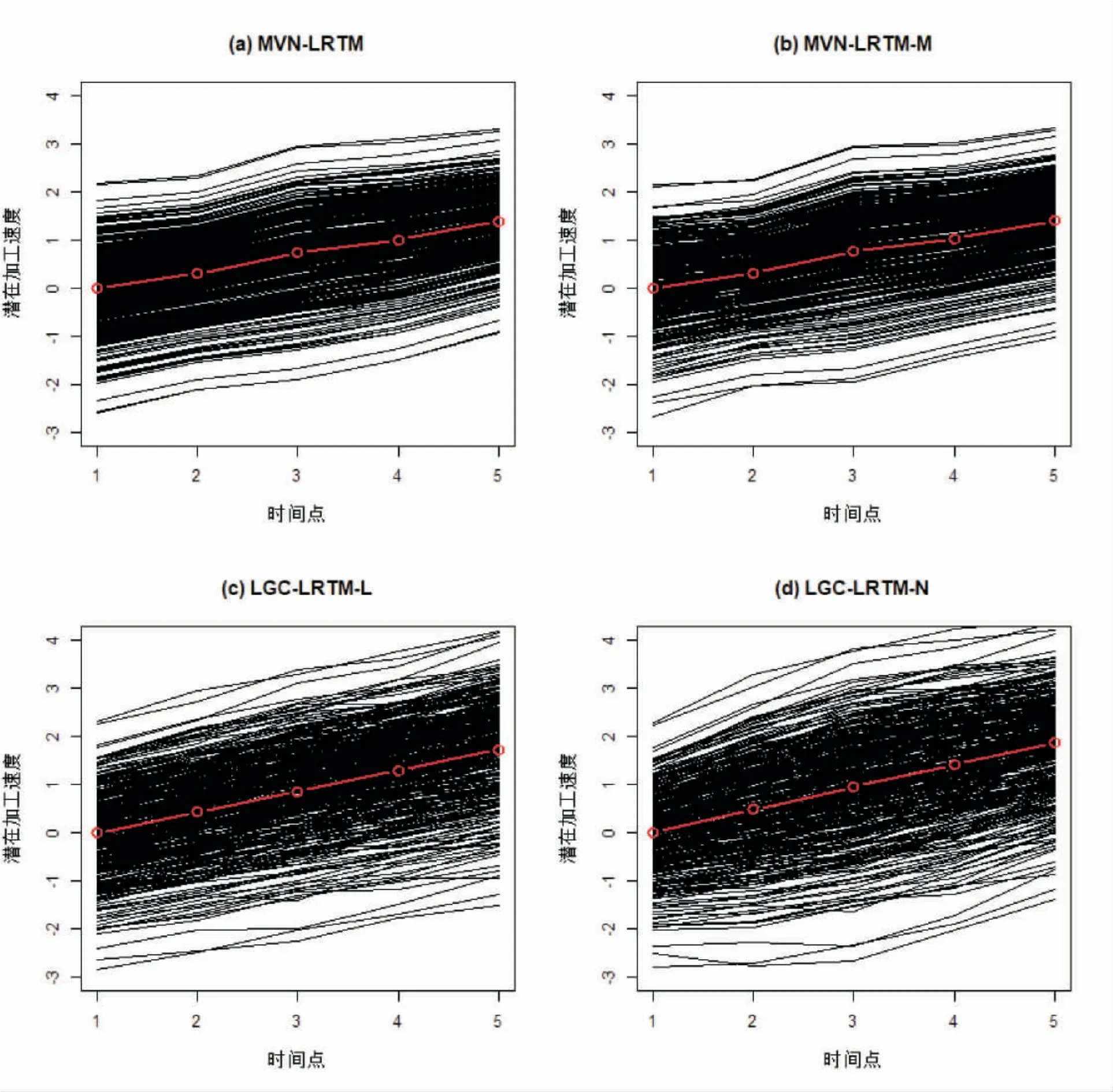
圖3 實證研究中潛在加工速度隨時間的變化趨勢

圖4 實證研究中所有模型對所有時間點上潛在加工速度的估計值之間的相關系數圖

圖5 呈現了四個模型的題目參數估計值。首先，四個模型的題目參數估計值之間具有較高的一致性，尤其是時間強度參數和時間精度參數。其次，同一類模型的時間區分度參數估計值相對更接近。

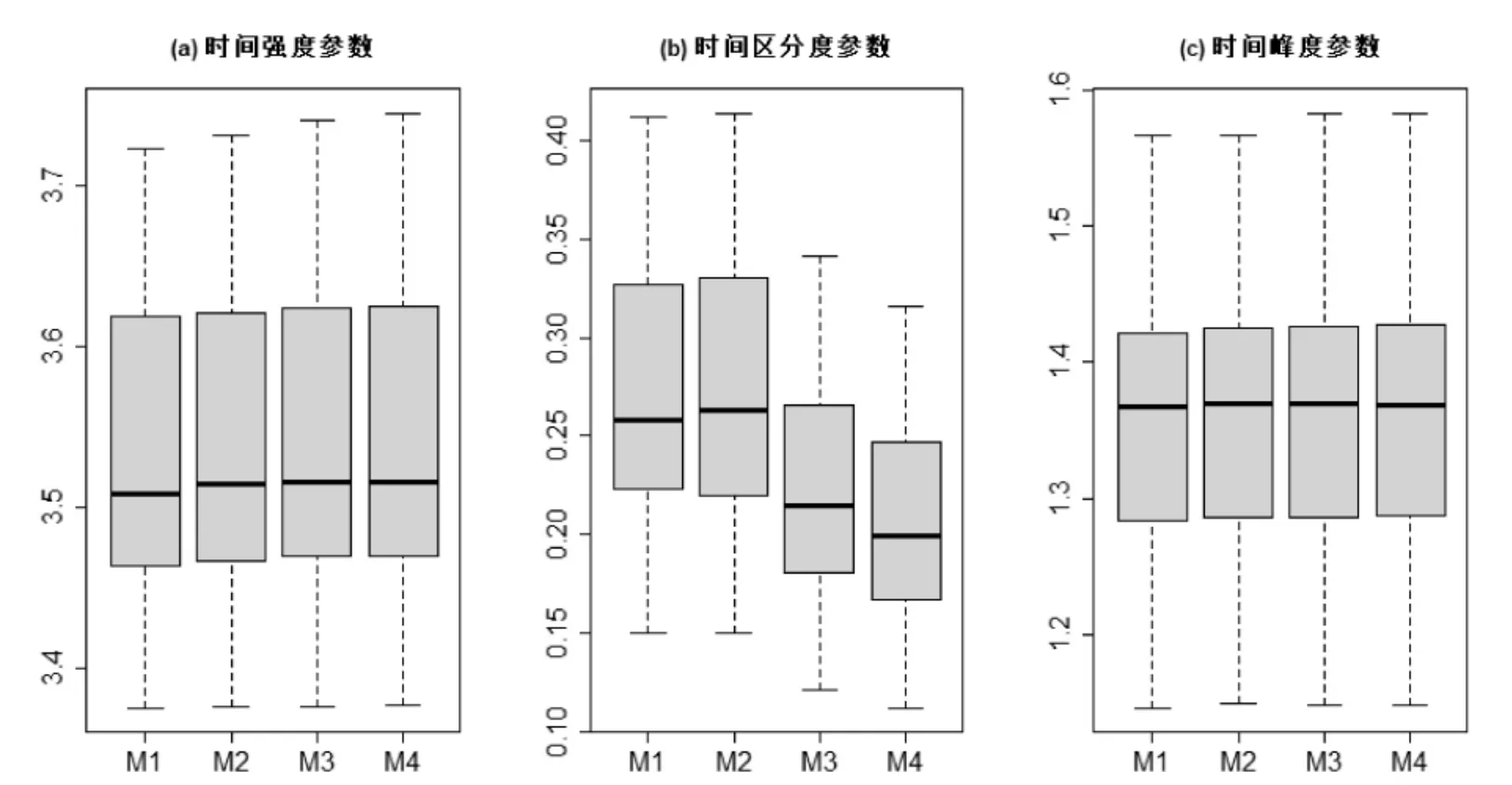
圖5 實證研究中所有模型的題目參數估計值

綜上所述，實證研究結果表明四個縱向RT 模型均具有實踐可應用性且對同一批數據的分析結果具有較高的一致性。此外，本研究還包含模擬研究，以探討模型的心理計量學性能，可見附錄S4。

3 總結與討論

為實現對個體潛在加工速度發展的客觀追蹤，本文基于多元正態分布和潛在增長曲線提出了四個縱向RT 模型。四個模型的測量模型一致，差異主要體現在描述潛在加工速度如何隨時間變化的結構模型上。具體而言，前兩個模型直接估計各時間點上的潛在加工速度，未直接關注變化的過程；相反，后兩個模型直接估計潛在加工速度隨時間的變化（增長）系數，沒有直接估計各時間點上的潛在加工速度。實證研究結果表明四個模型均有實踐可應用性，且它們的數據分析結果具有較高的一致性。模擬研究表明四個模型在不同模擬條件下的參數估計返真性良好，且兩個LGC-LRTM 對潛在加工速度的估計精度略高于兩個MVN-LRTM 的。總之，本文提出的四個縱向RT 模型具有實踐可應用性，且心理計量學性能良好，不僅豐富了心理與教育測量中縱向RT 數據的分析方法，也拓展了縱向潛變量模型的應用范圍。

限于精力和能力，本文也有一些局限有待未來研究做進一步探討。比如，盡管本文一次性提出了四個縱向RT 模型，但鑒于縱向數據分析的快速發展，目前還有諸如增長混合建模和多水平增長建模等多種縱向建模方法。未來可嘗試在縱向RT 數據分析中引入更多的縱向建模方法，以期進一步豐富縱向RT 數據的分析方法。其次，本文僅關注單維潛在加工速度隨時間的變化，隨著測評情境復雜性日益增加，如何追蹤多維潛在加工速度（詹沛達等，2020）隨時間的變化也值得關注和探究。詳細討論內容見附錄S5。