基于出行時段選擇的節假日免費政策優化*
何永明, 張磊, 曹劍
(東北林業大學 交通學院, 黑龍江 哈爾濱 150040)
2012年,國務院發布《國務院關于批轉交通運輸部等部門重大節假日免收小型客車通行費實施方案的通知》,規定在重要節假日期間(春節、清明節、“五一”國際勞動節和國慶節)對7座及以下小型車輛實行高速公路免費通行政策。該政策推動了更多出行者在重要節假日期間選擇高速公路出行[1],造成嚴重的高速公路交通擁堵,與方便節假日城際出行的初衷相悖[2]。節假日城際出行與工作日出行相差較大,具有明顯的集中出行和潮汐現象[3]。分析節假日期間出行特征,深入研究免費政策對出行選擇的影響,對制定合理節假日免費政策、減少集中出行現象具有重要意義。
城際出行特征主要包括出行時間、出行方式和出行距離等,且在節假日期間較容易受免費政策的影響[4]。因此,不少學者針對節假日免費政策和出行特征的關系展開研究,通過動態調整免費政策使出行者分散出行。由于出行特征具有離散性和隨機性,現有研究多通過在離散選擇上表現良好的Logit模型來模擬出行選擇過程[5]。馬瑩瑩等在傳統Logit模型的基礎上關注不同出行特征之間的相關性,引入考慮出行者異質性的分層Logit模型[6]。現有研究主要對出行特征的離散性進行分析,并在傳統Logit模型的基礎上構建出行選擇模型,缺少對其他離散選擇模型的探索。決策樹算法在處理離散特征上具有良好的擬合度,且在出行方式選擇上具有更高的識別率[7]。鑒于此,本文參考文獻[8],在考慮性別、年齡、家庭人均收入和出行目的等固有出行者屬性的基礎上,引入免費時段為擴展屬性,利用決策樹算法建立出行時段選擇模型,并設計多種分時段免費場景,考察各場景下出行比例的變化,選擇集中出行最少的場景作為節假日免費政策優化方案。
1 數據獲取和特征描述
1.1 數據獲取
節假日出行數據可以分為交通流數據和出行選擇數據。其中交通流數據來源于各省高速公路聯網數據庫,具有種類全面、數據量大等優點,方便從整體把握城際間高速公路交通流特征的變化趨勢。各省交通流數據統計標準不同,本文以2019年湖南省節假日期間交通流數據(見表1)為主要分析對象,其中包含機動車當量數、車型和車輛出入路徑等信息,分析免費政策對交通量的影響。
同時通過問卷調查采集湖南省2019年“五一”期間出行選擇數據,分析出行者屬性和免費政策對出行選擇的影響。問卷中出行者屬性包括性別、年齡、家庭人均年可支配收入、是否擁有汽車、出行目的和出行方式,同時統計出發日期選擇、出發時段選擇、返程日期選擇和返程時段選擇[9]等出行選擇屬性。共收集有效調查問卷635份作為數據樣本,出行者屬性見表2。本次調查中擁有汽車的受訪者高達73.43%,樣本反映了節假日期間受免費政策影響的主要出行群體。

表1 交通流數據
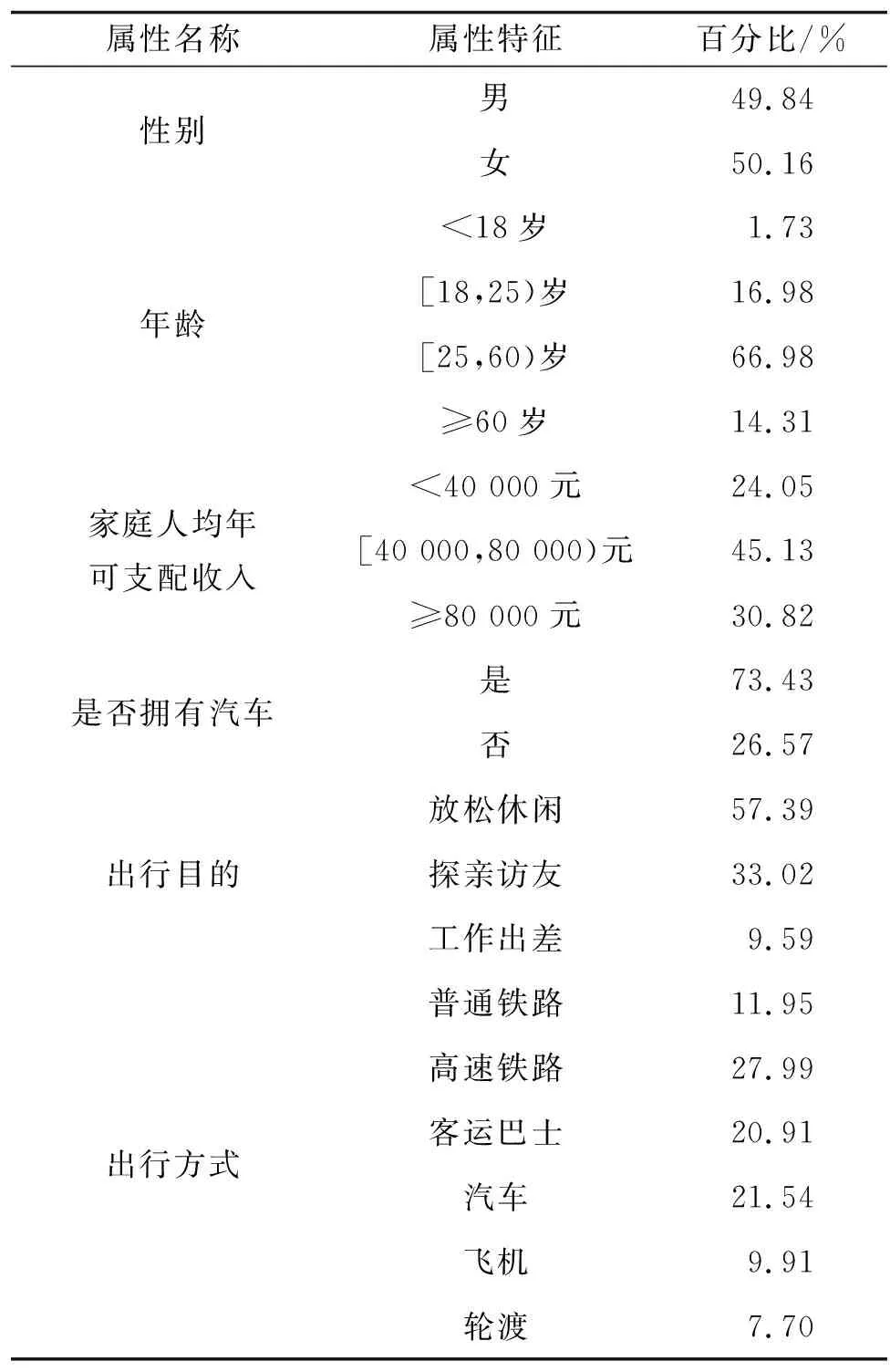
表2 出行者屬性
1.2 數據特征
2019年“五一”期間高速公路免費日期為5月1日0:00—5月4日24:00,為全面分析節假日出行時段選擇特性,采集“五一”前后各3 d共6 d的出行選擇數據,各日期出發和返程時段選擇見圖1、圖2,將出行時段選擇比例(該時段出行人數/總人數)作為評估參數,熱度由低到高通過不同顏色表示。
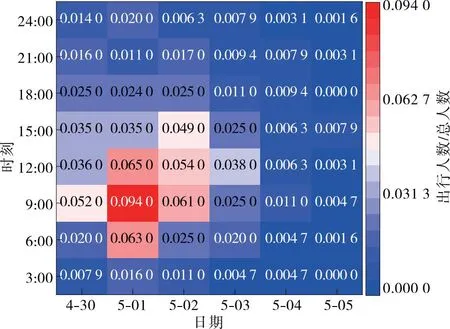
圖1 出發時段選擇熱力圖
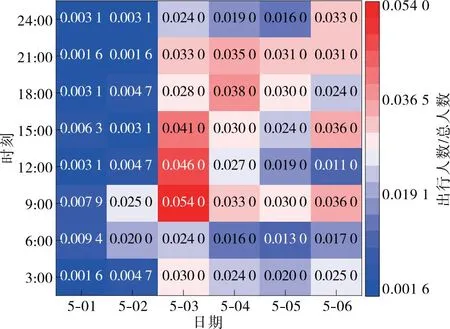
圖2 返程時段選擇熱力圖
由圖1、圖2可知:“五一”出行具有明顯的集中現象,出發時段集中于6:00—12:00,返程時段集中于9:00—15:00。出行選擇受主觀因素影響較大,可結合交通流數據進一步分析免費政策對節假日出行影響的顯著性。
2 免費政策影響分析
2.1 分析步驟
單因素方差分析法常用于討論被檢測樣本和參考樣本之間的差異性[10],具體參數見表3。利用單因素方差分析法探究免費政策和出行時段選擇的關系,只改變高速公路免費政策,其余因素在設計狀態下保持不變。通過對比F值和其在概率值α下的分位數,判斷免費政策的影響顯著性[11]。

表3 方差分析參數
總樣本共有r個水平,各出行者可抽象成相同分布的樣本xij。每一水平下樣本個數為n個,對不同水平下樣本觀測值進行計算,得總離差平方和SSST、組間平均離差平方和SSSA和組內平均離差平方和SSSE如下[12]:
(1)
(2)
SSSE=SSST-SSSA
(3)
SMSA、SMSE表示各狀態下樣本的均方和,其值為:
SMSA=SSSA/(r-1)
(4)
SMSE=SSSE/(n-r)
(5)
F值按式(6)計算。如果觀測值滿足F≥F(1-α)(r-1,n-r),則免費政策的影響顯著。
F=SMSA/SMSE
(6)
2.2 分析結果
結合采集的交通流數據,選擇春節、清明節、“五一”國際勞動節和國慶節4個法定節假日中5個不同日期交通量作為觀測樣本,以正常收費下工作日交通量作為參照樣本,則水平數r=5。各樣本中數據項數量ni為5,交通量分布見表4。
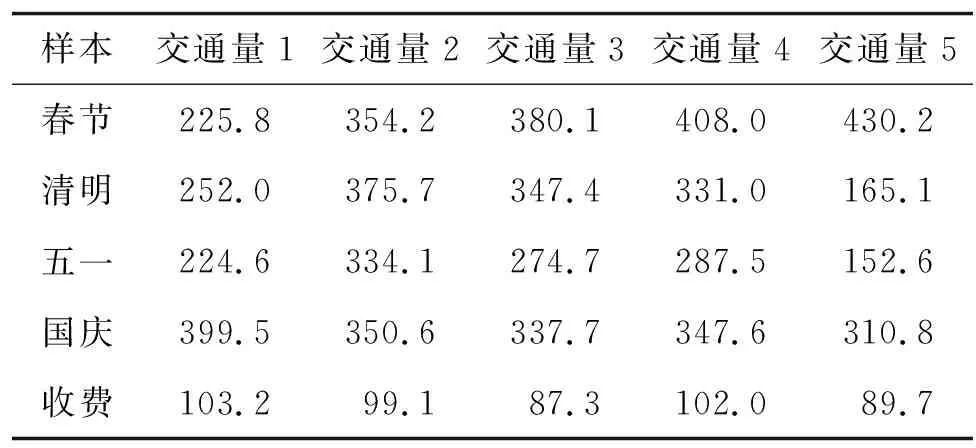
表4 樣本交通量分布 單位:萬輛/d
將表4中各樣本交通量代入式(1)~(6),利用SPSS軟件對不同樣本下交通量進行方差分析,結果見表5。
表5描述了各樣本交通量之間的差異性,其中組間平方和反映每組均值與總均值之間的離差,由免費政策變化所引起;組內平方和又稱誤差平方和,由隨機誤差所引起。查詢F檢驗臨界值表,F=12.856時顯著性水平遠小于0.05,表明免費政策對節假日交通量分布具有顯著影響。因此,有必要在建立出行時段選擇模型時添加免費政策作為特征參數。
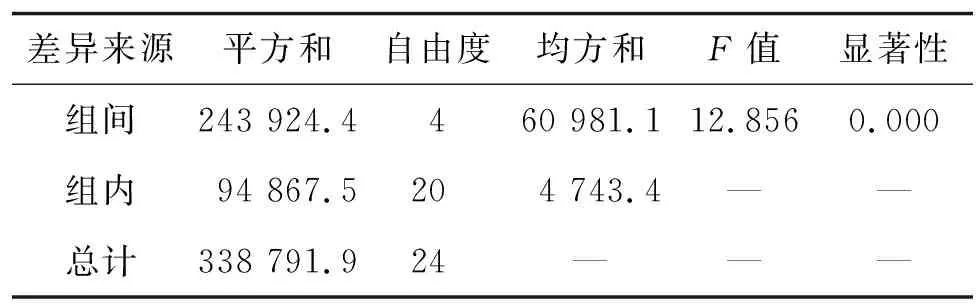
表5 方差分析結果
3 模型構建
3.1 模型結構
決策樹算法是一種不斷逼近離散函數值的方法,在處理數據后歸納特征生成可見決策樹,然后使用決策樹對新的測試樣本進行分類[13]。選擇決策樹算法作為出行時段選擇模型的理論框架,對不同決策屬性賦予對應權重,根據權重大小確定關鍵屬性,再對關鍵屬性的不同特征值下其他決策屬性的權重重新賦值。將上述決策過程通過樹狀圖表示,生成圖3所示決策樹結構。
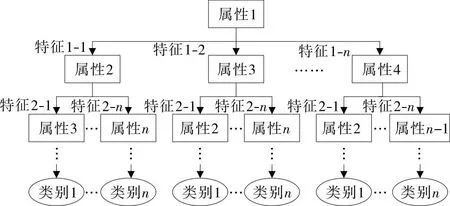
圖3 決策樹結構圖
由圖3可知決策樹結構具有以下特點:1) 決策樹由節點和有向邊組成,節點為關鍵決策屬性,有向邊代表各屬性的特征;2) 節點有內部節點和葉子節點兩種形式,內部節點為決策屬性,葉子節點為最終決策類別,即所選擇的出行時段;3) 各屬性在一條決策路徑中只出現一次;4) 每條決策路徑的屬性個數不確定,可為1~n中任一數值[14]。
根據決策樹結構,構建出行時段選擇模型須解決3個關鍵問題:1) 變量劃分,即確定決策屬性和特征值;2) 決策路徑生成,即確定關鍵屬性和路徑劃分函數;3) 模型優化,即對決策樹剪枝,提高模型的擬合優度。
3.2 變量劃分
構建模型所需的決策屬性包括免費政策、出行者屬性和出行選擇屬性。其中:免費政策作為擴展屬性可多次改變;出行者屬性與表2中各屬性的數據描述一致,可作為觀測值反映決策路徑變化;出行選擇屬性為出行選擇時段,以3 h為時間間隔,時間分布與“五一”期間出行選擇數據一致。為避免模型將特征值較多的屬性識別為連續變量,對出行者屬性和免費政策進行啞變量處理,結果見表6。
3.3 決策路徑生成
決策路徑生成的主要任務是選擇各屬性的不同特征進行分類,并確定下一層次屬性值。利用Python編程語言導入樣本數據,并通過Sklearn模塊中DecisionTreeClassifier類構建決策樹,重要參數的默認設置見表7。
基尼指數G是確定關鍵屬性和劃分路徑的重要指標,其原理見式(7)。基尼指數越小,分類結果越好,指數值最小的特征可作為決策路徑,并用于確定下一層次關鍵屬性。
(7)
式中:n為出行者數量;pk為關鍵屬性k選擇某條決策路徑的概率。
最小不純度K是一種閾值,可限制決策樹的增長,若不純度高于最小不純度,則繼續劃分下一路徑,反之停止增長。不純度可由信息熵表示,計算過程見式(8)。屬性k的不純度越低,信息熵越大。利用信息熵限定決策樹的增長,可以減少干擾路徑,使出行時段劃分更準確。
(8)
式中:i表示關鍵屬性k的具體特征;I為包含該屬性的所有特征值。
將出行時段以3 h為間隔劃分成8組,對擁有多個屬性的出行者X,通過迭代計算基尼指數和最小不純度K確定路徑決策順序Q={q1,q2,q3,…,qm},生成一棵最大深度≤m的二叉樹,流程見圖4。
決策樹中節點數量由基尼指數和最小不純度K共同決定,除葉子節點外,每層節點均對應兩個不同的下級屬性。先利用基尼指數確定屬性名稱,再對比屬性值和最小不純度K的大小;若屬性值大于K,則計算該屬性權重,并繼續獲取下一個屬性;反之保持K值不變,重新選取基尼指數最小的屬性。決策樹中葉子節點為可選擇的出行時段J,J={j1,j2,j3,…,jn},每個出行者最終只選擇一個出行時段。
3.4 模型優化

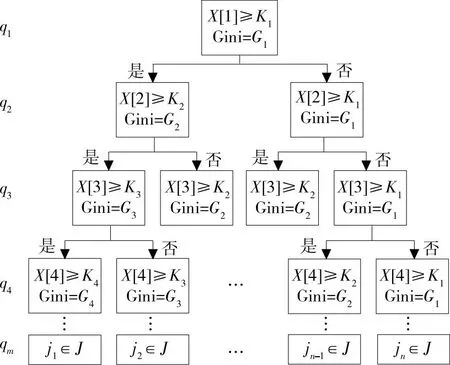
圖4 決策路徑生成流程
(9)
決策樹最大深度線性增加時,R2的變化見圖5。由圖5可知:隨著決策樹最大深度的增加,擬合優度R2呈上升趨勢。決策樹最大深度增加至14時,決策樹的葉子節點為單一出行時段,不再繼續生成決策樹,R2停止增長。此時出發時段選擇擬合優度為0.417,返程時段選擇擬合優度為0.324,表明該模型對出行時段選擇具有較好的擬合效果。
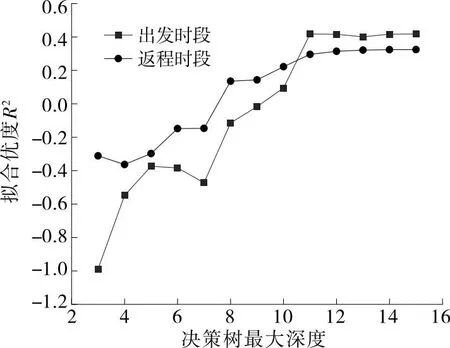
圖5 R2-決策樹最大深度折線圖
針對上述出行時段選擇模型,通過對決策樹進行剪枝避免出現過擬合現象。將樣本數據按7∶3的比例劃分為訓練集和測試集,采用后剪枝方法,在建立決策樹后由下而上提高模型穩健性。剪枝后評估標準包含精確度Mprecision、召回率Rrecall及F1分數。假設測試集中出行時段可分為時段A和時段B,則出行時段分類評估參數見表8,其中:TS與TO代表算法預測時段與實際出行時段一致,分別為A類和B類;FO代表算法預測時段為B,實際出行時段為A;FS代表算法預測時段為A,實際出行時段為B。TS、FO、FS、TO共同決定剪枝后模型的評估標準。

表8 出行時刻分類評估參數
精確度反映預測結果中預測正確的比例,按式(10)計算。召回率反映原樣本數據中被正確預測的比例,按式(11)計算。F1分數用于平衡精確度與召回率,按式(12)計算,F1越接近1,模型的穩健性越強。
(10)
(11)
(12)
式中:QTS、QTO為算法預測時段與實際出行時段一致的樣本數;QFO為算法預測時段為B,實際出行時段為A的樣本數;QFS為算法預測時段為A,實際出行時段為B的樣本數。
利用剪枝后的決策樹模型重新訓練測試集,得到表9所示出行時段選擇。由表9可知:剪枝后的決策樹模型擬合精確度和召回率的加權平均值均不小于0.70,且F1分數分別為0.70、0.71,表明該模型可以平穩預測出行時段選擇,且精確度較高。
4 免費場景仿真分析
4.1 分時段免費場景設計
調整高速公路免費政策,將全天免費改為分時段免費,收費標準與既有政策一致。采用場景仿真法設計不同收費組合并進行仿真分析,對比不同場景下各時段出行比例的變化。考慮到出行的連續性和時段劃分的一致性,將每日以3 h為一時間段分成8組,并依據日升、日中、日落劃分6種免費時段。免費場景設計如下:場景1為在節假日期間對所有時段均收費;場景2、場景3分別表示在白天和夜間收費;場景4、場景5、場景6在場景2的基礎上對時段進行進一步劃分,分別在6:00—12:00、9:00—15:00、12:00—18:00 3個時段收費(見圖6)。

表9 剪枝決策樹分類結果

圖6 免費場景設計
4.2 場景仿真結果
根據模型優化結果,選擇擬合優度較高且最大深度為14的剪枝后決策樹模型,以既有節假日政策為參考場景,結合圖6中各免費場景,改變模型屬性即免費政策的特征值進行仿真分析。根據仿真結果統計不同場景各時段出行比例,通過最大出行比例反映集中出行狀況,結果見表10。
最大比例可反映對應場景的集中出行狀況。由表10可知:不同收費時段的影響不同,單一的免費政策無法確保減少最大出行比例。例如在場景6中對12:00—18:00時段(組合5、6)收費,更多的出行者選擇在其他時段出行,導致最大出行比例增加。綜合出發和返程場景下最大出行比例,場景2下集中出行現象最少。

表10 不同場景下最大出行比例
結合圖1、圖2,選擇集中出行人數最多的5月1日和5月3日對場景2各時段出行比例進行統計,結果見圖7。
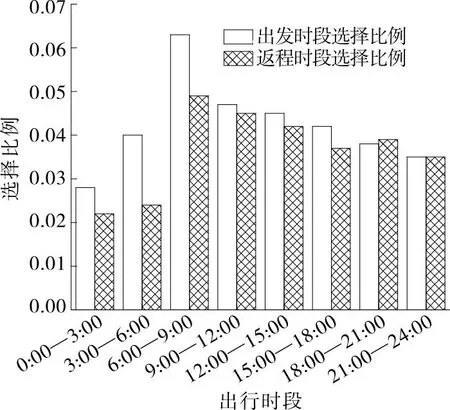
圖7 場景2出行時段選擇比例
由圖7可知:出行選擇比例最大的時段為6:00—9:00。與參考場景相比,由于白天對高速公路車輛進行收費,選擇夜間出行的人數增多,高峰小時出行比例下降。因此,節假日期間在6:00—18:00時段對高速公路進行收費,并對夜間其余時段免費通行,可有效緩解因集中出行導致的交通擁堵。
5 結論
把握出行時段選擇特征是制定和評價節假日高速公路免費通行政策的重要前提。本文通過構建基于決策樹算法的出行時段選擇模型,利用場景仿真法討論不同免費時段對集中出行的影響。結果表明,節假日高速公路免費通行政策對出行選擇具有顯著影響,導致高速公路交通量增加和潮汐出行;基于決策樹的出行時段選擇模型可以綜合考慮免費政策、出行者屬性和出行選擇屬性,較好地擬合出行決策;不同收費時段的影響差異較大,在6:00—18:00時段對高速公路進行收費可以有效減少集中出行。
該模型主要對免費時段進行討論,缺少對交通方式及出行距離的聯合分析。可綜合考慮不同里程收費對交通方式分擔率的影響,更全面地分析節假日高速公路免費通行政策的優化方向。

