基于有序Logit模型的高速公路追尾事故持續時間分析*

陳喆, 巫立明, 楊恒旭, 溫惠英, 趙勝

(1.廣東聯合電子服務股份有限公司, 廣東 廣州 510075;2.華南理工大學 土木與交通學院, 廣東 廣州 510640)

高速公路由于車輛運行速度快、交通流量大,存在較大的事故隱患和風險。相關研究顯示,高速公路的受傷率、死亡率及百公里事故率是普通公路的3倍以上[1]。高速公路交通事故在造成人民群眾生命財產損失的同時,還會導致高速公路交通擁堵甚至路網癱瘓[2]。在高速公路交通事故中,常見的事故類型有追尾、翻車、撞擊護欄、貨物灑落、側面碰撞等,追尾作為發生頻率最高的高速公路事故類型之一,其處置時間過長,容易造成二次事故的發生,進而導致更大的生命財產損失與通行能力下降。

交通事故發生后,第一時間對其持續時間進行預測評估有利于后續相關救援疏散工作計劃制定。近年來,眾多學者開展了交通事故持續時間預測研究,形成了兩類主要方法,分別為基于人工智能的方法和基于統計的方法。在人工智能學習模型方面,姬楊蓓蓓等采用貝葉斯方法建立決策樹預測模型,對交通事故持續時間進行了預測[3];何珂等基于山西省2 115起高速公路隧道交通事故數據,使用主成分分析和隨機森林組合模型對隧道交通事故持續時間進行了預測[4];紀柯柯等結合多種文本分類算法,構建V-Fisher有序聚類模型,提升了對交通事故持續時間的預測效果[5];Tang J. J.等基于華盛頓事件系統中2 565起交通事故數據,建立K-Means和XGBoost算法進行了事故持續時間預測[6]。基于人工智能學習模型的事故持續時間預測具有較好的性能,但可解釋性較差,且對樣本量的要求較高,需要豐富的數據樣本及標簽。基于統計方法的交通事故持續時間預測模型主要分為概率分布模型、線性回歸模型和基于風險的模型。Hou L.等建立非比例風險模型,基于西雅圖2 584起高速公路交通事故樣本,分析了事件、時間、地理、交通和運營對事件清除時間的時變影響,發現涉及重型卡車、夜間、周末等18個因素對清除時間有顯著影響[7];Ding C.等分別針對事故響應時間、清除時間建立二元概率模型和切換回歸模型,分析了事故類型、時間、環境等因素的影響[8];夏正豐應用多元回歸方法建立了高速公路交通事故持續時間預測模型[9];Zou Y. J.等利用分位數回歸方法和Copula模型分析了美國西雅圖高速公路交通事故持續時間的影響因素[10];Wali B.等對固定參數回歸、隨機參數回歸與基于分位數回歸的事故持續時間模型進行對比,結果顯示隨機參數模型的預測結果更準確[11]。以往的研究多是基于歷史事故數據對高速公路交通事故持續時間進行分析,較少考慮不同事故類型的事故持續時間的差異,且受限于數據采集難度,未充分考慮事故發生前后短時交通流參數變化對高速公路追尾事故持續時間的影響。基于高速公路追尾事故持續時間的有序性,本文將追尾事故持續時間分為3個等級,綜合考慮追尾事故信息與事故前后短時交通流運行狀況,運用有序Logit模型和邊際效應分析高速公路追尾事故持續時間的影響因素,為高速公路交通管理部門制定追尾事故救援及事故后交通疏散方案提供依據。

1 數據描述

研究數據來自廣東省高速公路主線ETC(電子不停車收費系統)門架數據及交警記錄的交通事故數據,基礎數據結構完整、字段齊全,具有良好的精度。通過數據匹配與數據挖掘進一步提取交通流數據與事故信息,其中交通流數據主要字段包括高速公路ETC門架監測的交通流量、交通密度、區間速度等,交通事故數據主要字段包括事故類型、涉事車輛類型、涉事車輛數、事故持續時間、占據車道情況及事故發生地點車道數、上下游路段交通設施布局等。通過對上述交通流數據、事故數據及道路數據進行匹配,得到925起高速公路追尾事故數據及發生前后短時交通流參數,為高速公路追尾事故持續時間分析及預測提供數據基礎。

如表1所示,所選數據集中高速公路追尾事故持續時間最大值為721.00 min,最小值為14.00 min,平均值為88.25 min,均方根為107.37 min。其中事故持續時間為50～100 min的追尾事故數量最多,約占全部追尾事故的52%(見圖1)。

由于存在多個難以觀測的變量影響事故持續時間,準確的追尾事故持續時間往往難以預測。高速公路交通管理部門在進行事故救援及事故后交通疏散時并不需要獲知事故準確的持續時間,而是需要根據預測的追尾事故持續時間長短將事故進行分級,以制定不同的事故處置方案。鑒于此,區別以往按照傷亡人數、財產損失對交通事故的分類,依據采集的925起追尾事故持續時間的分布及追尾事故對道路交通的影響,將追尾事故分為輕微追尾事故(事故持續時間小于100 min)、一般追尾事故(事故持續時間為100～200 min)和嚴重追尾事故(事故持續時間大于200 min)。

表1 高速公路追尾事故持續時間統計

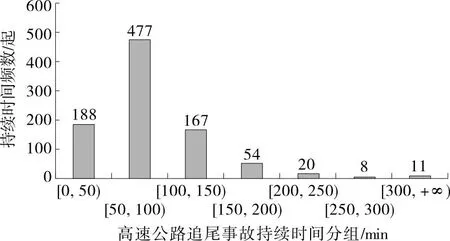
圖1 高速公路追尾事故持續時間頻數分布

高速公路追尾事故的持續時間與事故發生時間、涉事車輛類型、涉事車輛數、傷亡人數、占據車道情況及交通流狀況等密切相關[11]。因此,以追尾事故持續時間的3個等級為因變量,從事故發生時間、涉事車輛類型、傷亡情況、車道情況、事故發生前后交通流運行狀況五方面選取12個自變量進行分析,變量定義見表2。

表2 變量編碼及描述

續表2

由表2可知:因變量是三分類的有序變量,且持續時間逐漸遞增,而自變量中既有連續變量又有分類變量。其中二分類變量為事故發生日期、晝夜劃分、時段劃分及占據路肩情況,多分類變量是指多于2種選擇的變量,將涉事車輛類型劃分為僅小車、僅貨車、貨車與小車、有客車、有特種車五類。事故信息中,涉事車輛數、受傷人數及占據車道數為連續變量。考慮到事故發生前后交通流運行狀況可能對事故清理造成影響,將事故發生前后10 min內路段平均速度及到達上游門架的車輛數也作為自變量,探究其對追尾事故持續時間的影響。交通流影響因素中,追尾事故發生前后10 min內路段平均速度及到達事故發生點上游門架的交通量均為連續變量。

2 模型構建

多項Logit模型可視為二元Logit模型的拓展,二者的差異在于,二元Logit模型的被解釋變量只有0和1兩個取值,而多項Logit模型涉及被解釋變量有多個取值的情形。多項Logit模型基于效用理論擬合自變量與包含多個類別的分類變量間的內在關系。假定事故影響因素相互獨立,且服從Gumbel分布(Ⅰ類廣義極值分布),對于任一交通事故i,事故持續時間等級的效用函數為:

Si,k=βkXi+εi,k(k=1,2,3)

(1)

式中:Xi為事故i對應的影響因素觀測值組成的向量;βk為這些因素對應事故持續時間等級k的回歸系數組成的向量(包括常數項);εi,k為隨機項。

有序Logit模型主要用于處理因變量為有序變量的多分類結果,屬于多項Logit模型的拓展[11],在多分類的交通事故等級預測中表現出較好的性能。傳統有序Logit模型中,假定解釋變量的系數是固定的,高速公路追尾事故持續時間第j個等級的有序Logit模型為:

(2)

式中:Yi為第i起追尾事故的持續時間等級;X為自變量向量;β為回歸系數向量;αj為第j追尾事故等級的截距;J為高速公路追尾事故持續時間劃分的等級數量。

本文將因變量(追尾事故持續時間)分為3個等級,有序Logit模型為:

(3)

P(Y=2|X)=P(Y≤2|X)-P(Y≤1|X)

(4)

P(Y=3|X)=1-P(Y≤2|X)

(5)

式中:xk為第k個自變量,k=1,2,…,K;βk為第k個自變量的回歸系數。

邊際效應可用于定量分析不同因素對因變量影響的強弱程度與變化趨勢[12],其表達式為:

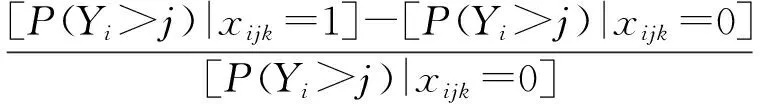
(6)

3 實例分析

3.1 參數結果分析

以廣東省某高速公路2020—2022年925起追尾事故的持續時間為研究對象,考慮到事故持續時間劃分等級具有有序性,通過回歸分析建立追尾事故持續時間的有序Logit模型。采用統計分析軟件Stata16.0進行求解,取顯著性水平為0.10,通過最大似然估計法估算得到有序Logit模型的參數結果(見表3)。

由表3可知:1) 受傷人數、占據車道數、追尾事故發生時間為工作日還是節假日、追尾事故發生時間為夜晚還是白天、事故發生后10 min內路段平均速度及涉事車輛類型對高速公路追尾事故持續時間具有顯著影響。占據車道數、受傷人數越多及追尾事故發生于節假日和白天都會導致追尾影響交通的持續時間更長。2) 占據車道數、受傷人數每增加一個單位,追尾事故持續時間等級上升的概率分別增加38%和46%,驗證了前人的研究成果[13]。節假日發生的追尾事故持續時間等級更高的概率是工作日的1.321倍,白天發生的追尾事故持續時間等級更高的概率是夜晚的1.788倍。3) 相較于涉事車輛類型均為小車,涉事車輛中含有大客車、貨車及特種車往往會造成更長的事故持續時間,這點與高速公路交通事故規律相吻合,即有大型車輛參與的交通事故往往伴隨著更大的事故影響范圍與事故嚴重程度。而隨著追尾事故發生后10 min內路段平均速度的增加,追尾事故持續時間等級更有可能下降,這可能是由于事故發生后上游駕駛員提高行車速度在短時間內駛離事故現場,以減少對現場交通的影響,為事故現場清理及應急救援提供良好條件。

表3 基于有序Logit模型的參數估計

表4為Pearson統計量和Deviance統計量擬合優度檢驗結果。Pearson和Deviance統計量的p值均大于0.1,表明在顯著性水平α=0.10的條件下模型的擬合效果較好。有序Logit模型平行性檢驗結果原假設是各回歸方程互相平行,平行性檢驗p=0.271>0.10,接受原假設,模型通過平行性檢驗,可進一步對高速公路追尾事故持續時間的影響因素進行分析。

表4 有序Logit模型的擬合優度檢驗

分別計算有序多分類Logit模型和無序多分類Logit模型的赤池信息量(Akaike Information Criterion,AIC)和貝葉斯信息量(Bayesian Information criterion,BIC),結果見表5。有序多分類Logit模型的AIC與BIC均低于無序多分類Logit模型,表明有序Logit模型的擬合優度更高。

表5 模型對比

3.2 邊際效應分析

結合邊際效應對表3中顯著的自變量進行參數解釋,結果見表6。

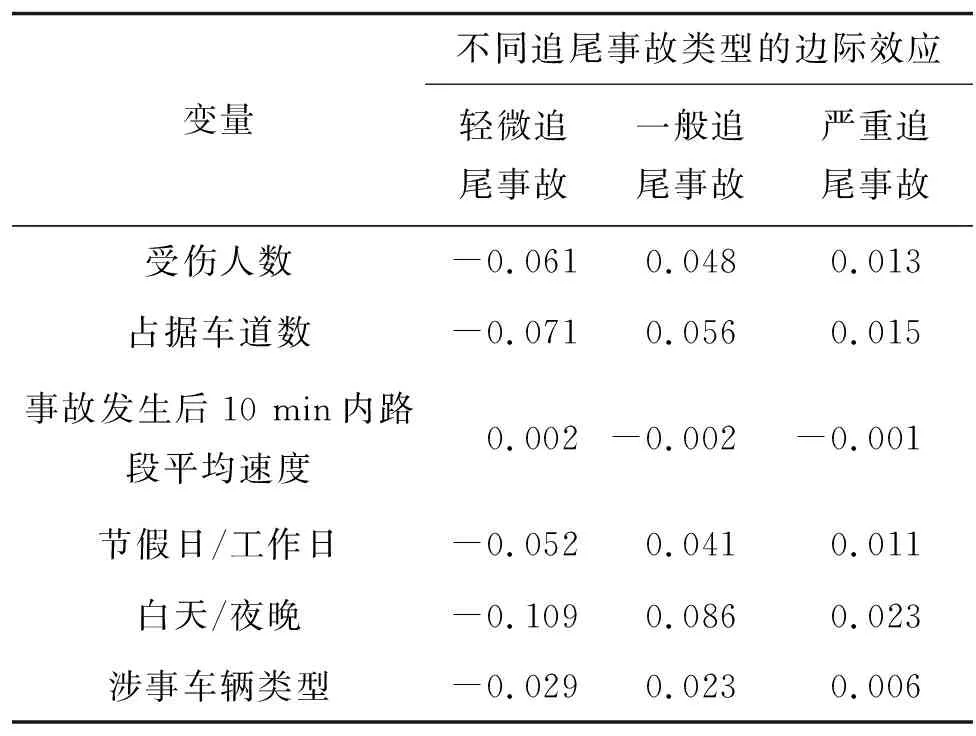
表6 邊際效應分析

由表6可知:1) 在90%置信水平上,受傷人數每增加1人,追尾事故為一般事故、嚴重事故的概率分別增加4.8%、1.3%,而輕微追尾事故的概率降低6.1%;占據車道數每增加1條,一般追尾事故、嚴重追尾事故的概率分別增加5.6%、1.5%,輕微事故概率降低7.1%;事故發生后10 min內路段平均速度每增加一個單位,一般追尾事故與重大追尾事故的概率分別降低0.2%、0.1%。2) 相較于工作日和夜晚,節假日與白天容易發生持續時間更長、嚴重程度更大的追尾事故。節假日期間一般追尾事故、嚴重追尾事故的概率分別增加4.1%、1.1%,白天時段一般追尾事故、嚴重追尾事故的概率分別增加8.6%、2.3%。這是由于節假日和白天高速公路交通量更大,給事故清理與應急救援帶來更大干擾,造成更長的事故持續時間。3) 在涉事車輛類型方面,涉事車輛中含有大客車、貨車及特種車會增加追尾事故的持續時間。

4 結論

(1) 以廣東省某高速公路2020—2022年925起追尾事故為研究對象,從事故發生時間、涉事車輛類型、傷亡情況、車道情況、事故發生前后交通流運行狀況5個方面選取12個自變量,以事故持續時間為特征將追尾事故劃分為3個等級,并將其作為因變量,分別構建無序多分類Logit模型和有序多分類Logit模型。結果表明,相較于無序多分類Logit模型,有序多分類Logit模型對高速公路追尾事故持續時間的擬合效果更優。

(2) 高速公路追尾事故占據車道數、受傷人數、事故發生時間、事故發生后10 min內路段平均速度及涉事車輛類型對事故持續時間具有顯著影響。

(3) 占據車道數和受傷人數越多、追尾事故發生于節假日和白天及涉事車輛中含有大客車、貨車及特種車輛會增加追尾事故的持續時間。

(4) 追尾事故持續時間隨著事故發生后10 min內路段平均速度的增大而減少,事故發生后10 min內路段平均速度每增加一個單位,一般追尾事故與重大追尾事故的概率分別降低0.2%、0.1%。