基于廣義有序Logit模型的運行速度安全性研究*

祁欣月, 楊燦

(西藏大學 工學院, 西藏 拉薩 850011)

根據國家統計局的資料,2001—2018年,約1/3的機動車死亡事故涉及超速行駛;2017年,52 274名司機參與了34 247起致命車禍,導致37 133人喪生,事故發生時17%的車輛超速行駛,26%的死亡司機中至少有1人涉及超速駕駛;與速度相關的事故約占總事故的1/3,在人為因素引起的事故中排名第二;2018年上半年,共有105 000起涉及受傷的交通事故,其中超速占13.8%[1]。可見,超速是交通事故的主要原因之一。在較高的速度下,駕駛員的判斷能力降低,無法正確操控車輛或判斷其他車輛的速度。車速越高,駕駛員的注視點越遠,視野越窄,同時制動距離增大,駕駛員應對危險或緊急情況的時間減少,會導致更多的碰撞。車速控制一直是交通安全領域的研究熱點,相關研究主要集中于限速、速度執法和駕駛員速度選擇等措施的安全效果評價[2]。

1 研究現狀

1.1 車速與事故的關系

車輛速度與道路安全之間的關系一直是交通安全研究的主題。Solomon D.根據四車道公路的數據研究車速與事故之間的關系,將撞車原因歸結于速度變化,并提出式(1)所示速度模型,該模型是關于車速和事故之間定量關系的早期研究[3]。

I=100.000 606 2Δv2-0.006 675Δv+2.23

(1)

式中:I為分段中的碰撞率;Δv為速度差,即某段中的運行速度與平均運行速度之差。

Solomon模型曲線為U形。速度差接近零時,事故率最低;速度差變大時,無論是在正向還是負向,事故率都增加。

1989年,瑞典進行了為期2個月的試驗,將限速從110 km/h調整為90 km/h。與1988年同期相比,汽車的平均速度降低14.4 km/h,事故次數減少21%,表明運行速度降低會降低事故率,提高道路交通安全性。

1993年,莫納什大學事故研究中心提出速度差和事故率之間的近似函數,稱為MUARC模型,表達式見式(2)。與Solomon模型類似,該模型中速度差與事故率成比例。

I=500+0.8Δv2+0.014Δv3

(2)

2004年,Elvik R.等提出一組反映車輛平均運行速度與事故次數或受傷嚴重程度之間關系的冪函數[4]:

(3)

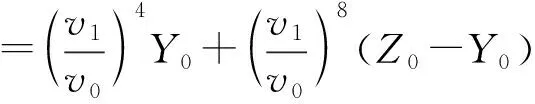
(4)

(5)

Y0)

(6)

(7)

Y0)

(8)

式中:v0、v1分別為采取交通控制措施前后的速度;Y0為速度變化前的碰撞次數;Z0為速度變化前的嚴重受傷人數。

Elvik R.還發現,與交通量變化相比,平均車輛運行速度變化對傷害事故的影響更大[5]。

1.2 期望速度和實際運行速度

期望速度ve(也稱為心理速度)是指駕駛員在道路運行中不受或基本不受其他車輛約束的情況下期望達到的最高安全速度。不同類型車輛具有不同的性能條件,條件良好的車輛能以較高的車速行駛,期望速度相應提高。駕駛員的期望速度因個性特征、駕駛技能和年齡等差異而有所不同[6]。受道路條件、交通流、氣候條件及運輸任務緩急等因素的影響,期望速度在某種程度上是一個理想值,難以準確獲得。

實際運行速度是中等技能駕駛員在實際道路、交通流和氣候條件下可以保持的安全速度,通常將測量速度的第85%位速度v85作為運行速度。Agent K. R.等以第85%位速度作為限速依據,并建議小型汽車和貨車分別采用不同的限速[7]。

1.3 實際運行速度模型

實際運行速度隨期望速度波動。當道路條件和交通流達到預期的理想條件時,車輛將以期望速度行駛。由于道路線形、車輛性能或交通流的變化,車輛實際運行速度將低于預期[8]。因此,設定各區段的期望速度是準確預測運行速度的關鍵。

1987年,Lamm R.等在84條彎曲路段進行車輛行駛試驗,得到了基于豎曲線曲率變化和半徑的車輛運行速度預測模型[9]:

v85=95.78-0.076RCCR,R2=0.842

(9)

式中:RCCR為曲率變化率。

張琦等的研究表明切線長度、曲率半徑、曲線長度、缺陷角、縱坡和超高等道路幾何參數均與運行速度相關[10]。

2008年,Memon R.等提出基于切線長度、圓曲線角度和切線速度的車輛運行速度模型[11]:

0.163ω,R2=0.62

(10)

式中:R為水平曲線半徑;v85,Tmax為切線上第85%位速度的最大值;T、ω分別為平曲線的切線長度和偏轉角度。

2011年,Syed A. S. K.等根據曲線半徑和切線速度對運行速度模型進行優化,得到以下模型[12]:

R2=0.532

(11)

式中:v85MC為中間曲線的第85%位速度;RRC為圓曲線半徑;v85AT為接近切線的第85%位速度。

JTG/T B05—2004《公路項目安全性評價指南》提出了公路運行速度模型。JTG B05—2015《公路項目安全性評價規范》對低等級公路速度模型進行優化和改進,根據平曲線半徑和縱斷面坡度將評價路段分為切線段、縱坡段、平曲線段、彎坡組合段、隧道段、互通式立交段等進行計算。對于平曲線路段,分別預測曲線中間和末端的運行速度,預測模型見表1;對于縱坡路段的末端,根據表2計算運行速度;對于彎坡組合路段,分別預測曲線中間和末端的運行速度,預測模型見表3[13]。

表1 平曲線路段運行速度預測模型

表2 縱坡路段速度換算模型

表3 彎坡組合路段運行速度預測模型

2 基于Logit模型的運行速度安全性研究

已有文獻針對車輛速度與道路安全之間的關系進行了研究,并對實際運行速度和期望速度模型進行了細化分析,闡明了車輛運行速度受道路條件、交通流、氣候條件等因素影響的規律。但對高速公路運行速度與事故嚴重程度的關系、高速公路安全受小車和大車運行速度及其他道路環境因素影響的研究較少。本文基于廣義有序Logit模型,以京滬(北京—上海)高速公路新沂至江都段2009—2011年的3 293起交通事故為例,對高速公路事故類型、事故嚴重程度與車輛運行速度的關系進行研究。該高速公路全長259.5 km,設計速度為120 km/h。

2.1 研究方法

序變量是對可能值進行排序的分類變量[14]。本文采用廣義有序Logit模型(GOLM)分析車速變量對事故的影響。有序離散結果模型(如有序Logit利潤模型)的主要假設是估計參數為常數,稱為平行回歸假設[15]。通過廣義有序Logit模型得到i級損傷的概率如下:

(12)

式中:P(*)表示特定損傷等級事故的發生概率;y為事故的損傷等級;i為事故損傷程度的特定類別;βi為指標對應的擬合系數;Xn表示車速變量;μi為第i級損傷對應的常量系數。

受限于固有的比例優勢假設,傳統的Logit分析無法涵蓋所有受傷嚴重程度,Wang X. S.[16]和Quddus M. A.[17]等對廣義Logit模型進行如下改進:

(13)

式中:β1為根據損傷嚴重程度確定的參數;X1、X2表示與受傷嚴重程度密切相關的自變量;β2為固定參數。

GOLM模型中使用的自變量見表4。其中交通事故嚴重程度遵循公安部的分級標準:輕微事故是指一次造成2人以下輕傷,或財產損失不超過1 000元的事故;一般事故是指一次造成1～2人重傷,或2人以上輕傷,或財產損失為1 000～30 000元的事故;重大事故是指一次造成1～2人死亡,或3～10人重傷,或財產損失為30 000～60 000元的事故;特大事故是指一次造成3人以上死亡,或10人以上重傷,或1人死亡同時8人以上重傷,或2人死亡同時5人以上重傷,或財產損失超過60 000元的事故。根據上述分級標準,京滬高速公路新沂至江都段2009—2011年的3 293起交通事故中,沒有一起是非常嚴重的事故。

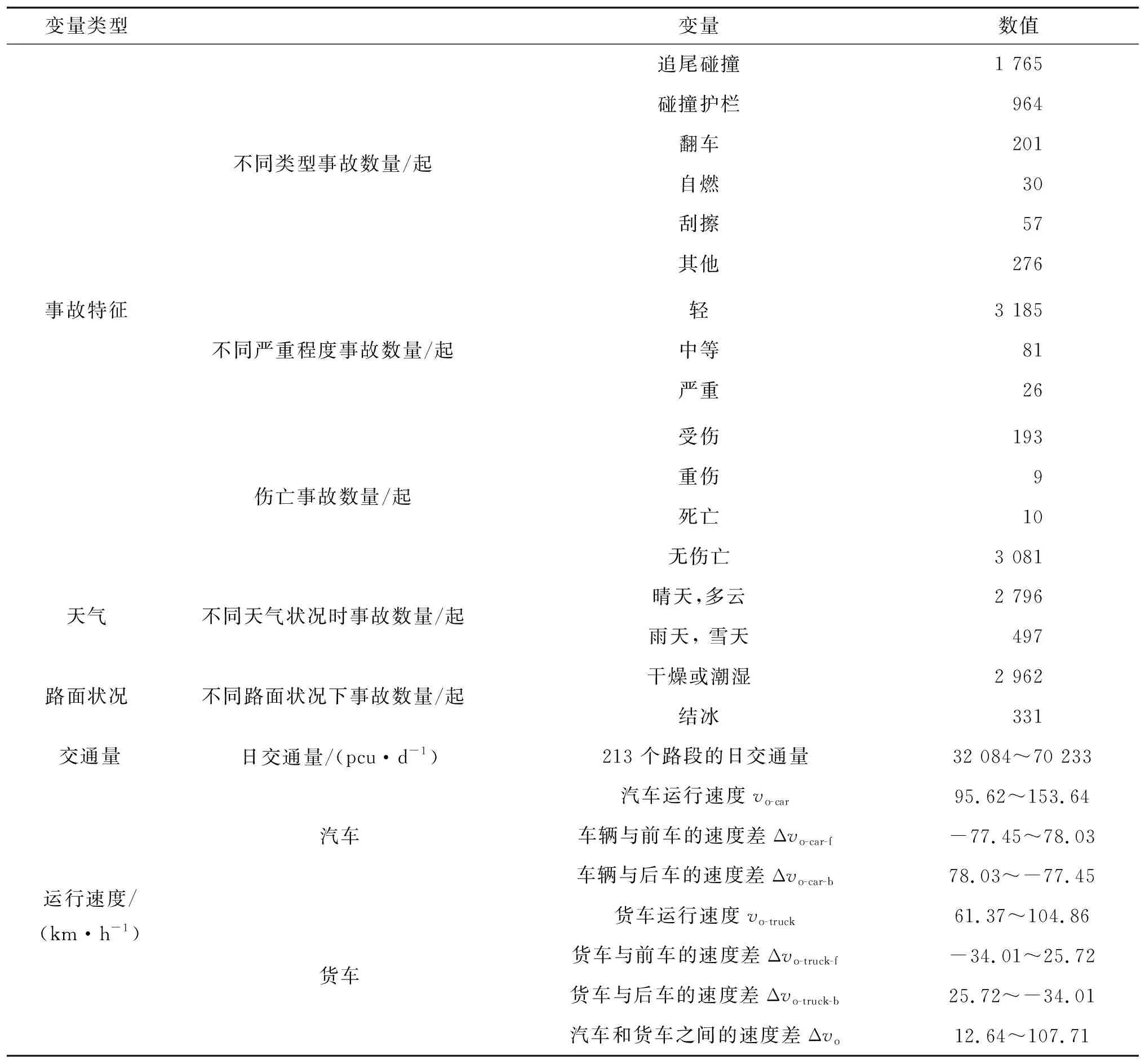
表4 GOLM模型中使用的自變量

由于數據信息有限,表4中交通量僅包括213個路段的日交通量。運行速度包括小型汽車和貨車的速度、相鄰路段之間速度差及每個路段內小型汽車和貨車之間速度差。相關研究表明,較高的速度方差會導致更多的事故[18]。

2.2 研究數據

(1) 道路設計施工圖。提供道路幾何要素的詳細信息,如橫斷面、水平線形、垂直線形、立交等。

(2) 事故記錄。事故記錄包含對每起事故發生時間、位置等的詳細描述,根據事故記錄,可以收集事故類型、事故嚴重程度、受傷或死亡人數、車輛類型等詳細信息。

(3) 道路管理機構報告的213個路段的日交通量。

(4) 依據表1～3中速度模型,按照不同的幾何特征分段計算小型汽車和貨車的運行速度。

(5) 根據實際運行速度調整期望速度。根據JTG B05—2015,汽車的期望速度為120 km/h,貨車的期望速度為80 km/h。當計算的車輛實際運行速度高于120 km/h、80 km/h時,使用期望速度值120 km/h、80 km/h。

3 模型計算結果分析

以事故類型和事故嚴重程度作為因變量,對自變量與因變量進行Pearson相關性分析,結果見表5。

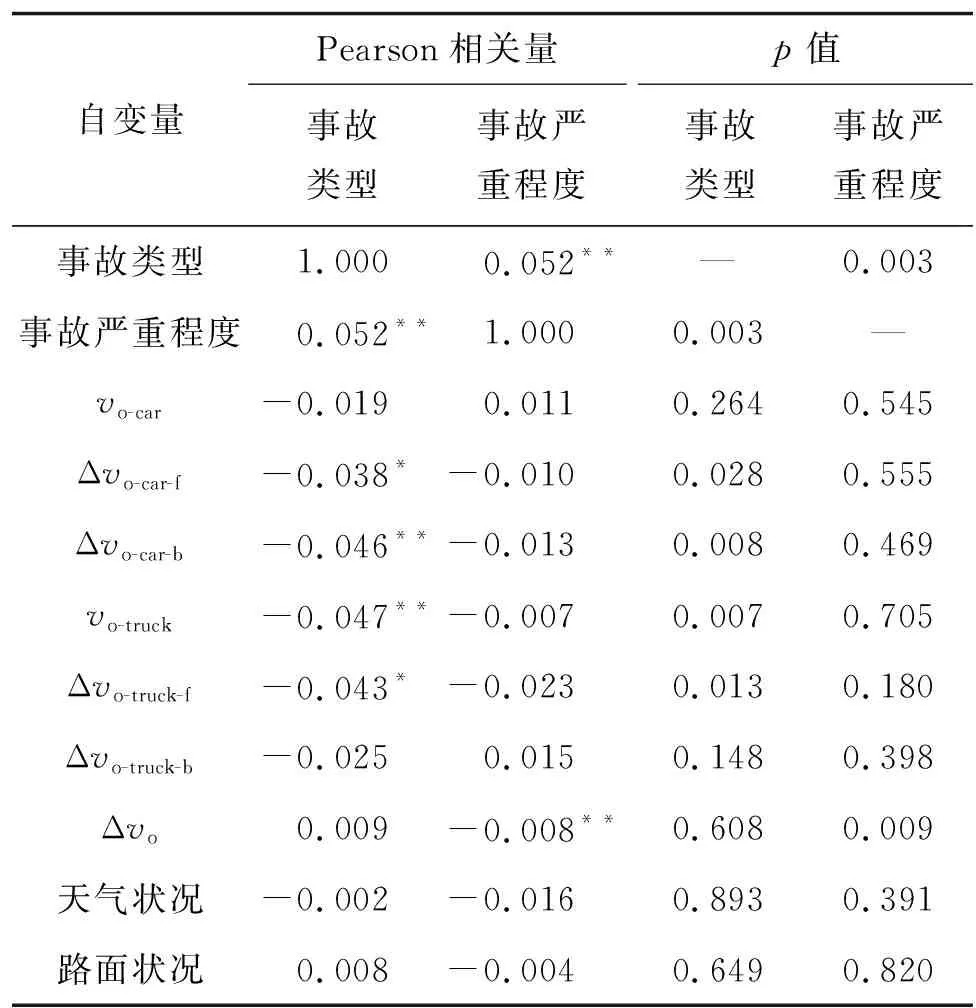
表5 自變量與因變量的Pearson相關性分析結果

由表5可知:事故類型與自變量的相關性優于事故嚴重程度。以事故類型為因變量的廣義有序Logit模型中,各參數的系數、標準誤差和p值見表6。

Baruya A.等研究傷害事故與車速之間的相關性,發現平均車速和速度差對事故的影響都很大,隨著平均車速的增加事故數量增加[19]。Ayati E.等認為平均車速增加,事故數量會隨著速度差的減小而減少[20]。Lassarre S.認為在相對固定的速度范圍內,車速變化對道路安全有顯著影響,車速值的影響較小[21]。Savolainen P.等認為致命事故率受車輛間速度差的影響較大[22]。由表5、表6可知:1)vo-car、Δvo-car-b、Δvo-truck-b(p<0.01)是影響事故類型的重要因素,與文獻[19-20]的研究結論相符。高速行駛時,視線變遠,視野范圍變窄,駕駛員反應變慢,更容易做出錯誤的決定。此外,由于多種幾何組合變化較多,在速度差較大的道路區間,對車輛速度的控制更困難,特別是車輛進入或駛出速度差較大的坡道時,發生事故的頻率更高。2) 貨車的運行速度不如速度差重要,與文獻[21-22]的研究結論一致。3)vo-car、Δvo-car-f、Δvo-car-b、Δvo-truck-b具有統計學意義,以Yv表示它們對因變量的影響,根據表6中的回歸結果,可得到式(14)。說明當小型汽車的實際運行速度和后段貨車的速度差較高時,對事故的影響將更大,與文獻[23]的研究結論一致。4) 對于事故嚴重程度,只有Δvo是重要參數,其他參數(如汽車或貨車速度)沒有顯著相關性。這一結果與Garber N. J.等的研究結論一致,他們研究發現事故率和平均速度之間沒有明顯的聯系[24]。5) 就天氣條件而言,雨雪天的安全風險比晴天、陰天高30.1%。因為雨雪天道路很滑,駕駛員的視力很差,安全風險增大。

Yv=0.011 20vo-car-0.009 52Δvo-car-b+

0.012 12Δvo-truck-b

(14)

4 結論與建議

本文研究速度及速度差對事故類型和事故嚴重程度的影響。以京滬高速公路新沂至江都段為例,根據道路幾何結構將其分割為213個不同路段,并計算每個路段的運行速度。采用廣義有序Logit模型對該路段2009—2011年的3 293起事故數據進行分析,量化運行速度、相鄰路段的速度差及不同車型之間速度差對事故類型和事故嚴重程度的影響。分析發現顯著的影響因素包括與相鄰路段的速度差、車輛運行速度和天氣條件。

可采取如下措施改善道路交通安全:1) 在匝道等運行速度由高到低的過渡區域,采取合理的減速措施,如設置減速帶、振動標記、光學標記、限速標志、安全警示牌等,若與相鄰路段的速度差過大,在相應位置安裝減速標志、警告標志等交通安全標志,提醒駕駛員提前減速,確保行車安全。2) 為減少汽車和貨車之間的干擾,建議采用不同車型的車道分配模式。設置交通標志和路面標記,提醒貨車司機在外車道行駛、汽車司機在內車道行駛。3) 平原地區公路的水平和垂直線形通常優于山區,長切線段會提高駕駛員的期望速度。可在這種路段設置限速標志、安全警告標志、減速帶等安全設施,提醒駕駛員注意安全,并嚴格執行限速,確保行車安全。

未來的研究方向如下:1) 利用更真實的事故數據研究影響交通事故的因素,包括駕駛員性別和年齡、實時交通量、事故發生位置、事故發生時間和天氣狀況等。2) 收集實時車速作為面板數據,并與計算的運行速度進行比較,研究實時車速對交通事故的影響。3) 根據實時車速建立模型預測事故,為道路設計、管理和駕駛教育方案制定提供更合理的指導。