基于灰色馬爾可夫模型的連續配筋混凝土復合式瀝青路面性能研究*
姚嘉昊, 趙健, 杜靜, 朱昂, 李江昆
(長沙理工大學, 湖南 長沙 410114)
連續配筋混凝土復合式瀝青路面(以下簡稱復合式瀝青路面)是將高強度CRC(連續配筋混凝土)板和柔性AC(瀝青混凝土)面層相結合的剛柔復合式路面結構,它綜合了不同路面材料的特性且能最大限度利用地方材料,具有整體強度高、行車舒適性好、使用壽命長、維修費用少等優點[1-2],是重載交通長壽命瀝青路面結構的發展方向。目前中國部分高速公路采用復合式瀝青路面對舊混凝土路面進行改造,研究復合式瀝青路面性能衰減規律,可為復合式瀝青路面養護決策提供依據[3-6]。程焰兵采用ABAQUS模擬了移動荷載作用下復合式瀝青路面的動力響應[7]。程小亮等對復合式瀝青路面設計方案進行了優化[8]。周婷針對復合式瀝青路面結構存在的層間滑移問題,通過層間黏層材料剪切疲勞試驗、層間剪應力有限元分析,提出了基于層間剪切疲勞的瀝青層厚度設計方法,完善復合式瀝青路面結構設計[9]。但缺乏針對復合式瀝青路面性能衰減規律的研究。
路面性能預測模型可以分為確定型和概率型兩類。確定型模型的預測結果是一個確定值,而瀝青路面性能衰減受荷載、環境、路面結構、交通量、養護水平等因素影響是一個動態過程,如果采用確定型模型預測路面性能衰減趨勢,無法反映瀝青路面性能動態變化的不確定性。概率型模型可預估瀝青路面性能的分布概率,其中應用最廣泛的是馬爾可夫模型[10]。本文依托湖南潭邵(湘潭—邵陽)高速公路K1054+000—K1100+500路段復合式瀝青路面,根據該路段2016—2021年路面狀況指數IPCI檢測數據,選取灰色馬爾可夫模型預測復合式瀝青路面的衰變趨勢。
1 灰色馬爾可夫模型
1.1 灰色GM(1,1)模型
灰色預測模型適用于數據量較少或數據不完全的情況,通過構建灰色預測模型,對某事物如路面性能的發展規律作出模糊性描述。其基本思想是對原始數據進行累加,以減小原始數據隨機性的影響,使其呈現明顯的變化規律[11]。
(1) 構建原始序列:
X(0)={X(0)(k);k=1,2,…,n}
(1)
式中:X(0)(k)為原始數據。
(2) 對原始序列進行累加,生成一次累加數據序列:
X(1)={X(1)(k);k=1,2,…,n}
(2)
式中:X(1)(k)為前k項原始數據的累加和。
(3) 確定灰色GM(1,1)模型參數。式(3)為灰色GM(1,1)模型。為確定模型參數u、a,按式(4)、式(5)構造矩陣B和向量Yn,采用最小二乘法按式(6)求解u、a。
(3)
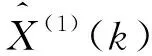
(4)
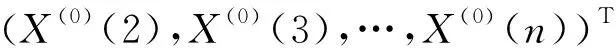
(5)
(6)
(4) 按式(7)求解預測數據。
(7)
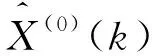
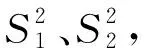
(8)
(9)
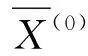
(10)
(11)
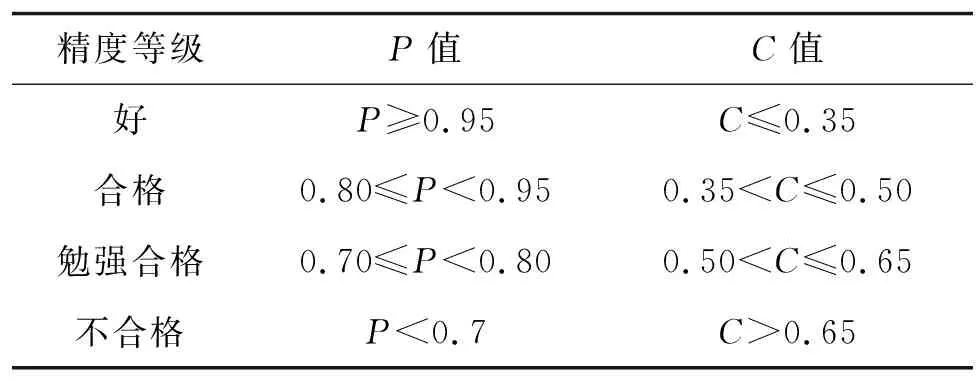
表1 模型精度等級劃分標準
1.2 馬爾可夫模型
馬爾可夫預測模型是概率型模型,其預測結果只與當前狀態有關,具有無后效性。其主要內容是構建狀態轉移概率矩陣,該矩陣表示某事物如某路段的路面性能在預定時間內從某一狀態轉移到另一狀態的概率。
為了使馬爾可夫模型適應路面性能預測,做如下假定:1) 狀態轉移概率不隨時間變化;2) 存在有限個路面性能狀態;3) 路面性能狀態轉移只與當前狀態有關,即具有無后效性。
馬爾可夫模型的數學表達式如下[12-13]:
P(xt+1=j|xt=it,xt-1=it-1,…,x1=i1)=
P(xt+1=j|xt=it)
(12)
式中:{xt,t=1,2,…}為一離散的隨機變量序列;t表示每一個變量值xt所對應的時間點;{it,t=1,2,…}表示不同時間點的狀態;P(xt+1=j|xt=it)為轉移概率。
由于系統中存在n種狀態,描述各種狀態轉移到其他狀態的概率矩陣如下:
(13)
式中:Pnn為系統各狀態轉移的概率。
狀態轉移向量如下:
X(n0+n)=X(n0)Pn
(14)
式中:X(n0)為當前時刻的狀態轉移概率向量;P為狀態轉移矩陣;X(n0+n)為預估n年后的狀態轉移概率向量。
2 實例分析
2.1 工程概況
2016年,潭邵高速公路K1054+000—K1100+500路段實施大修,將舊混凝土路面改造為復合式瀝青路面。收集該路段2016—2021年路面狀況指數IPCI檢測數據,運用灰色馬爾可夫模型對路面狀況指數IPCI衰減趨勢進行預測。
2.2 基于灰色GM(1,1)模型的路面狀況指數預測
2.2.1 數據處理與檢驗
以每公里檢測數據的平均值表示路面狀況指數IPCI,原始數據見表2,原始數據的累加數據見表3。
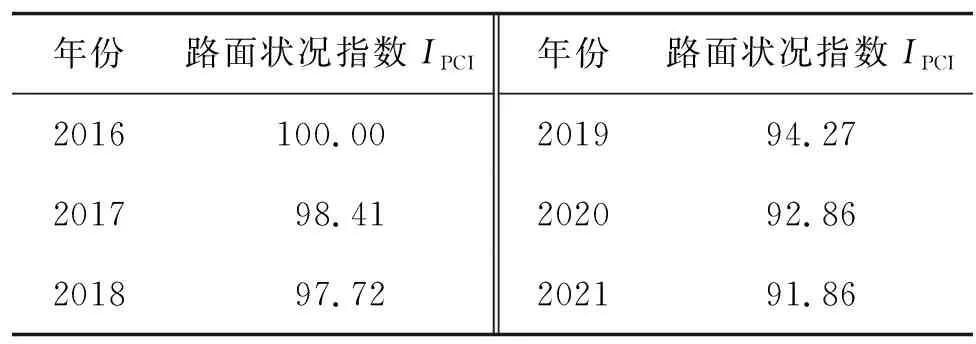
表2 2016—2021年路面狀況指數IPCI 檢測數據
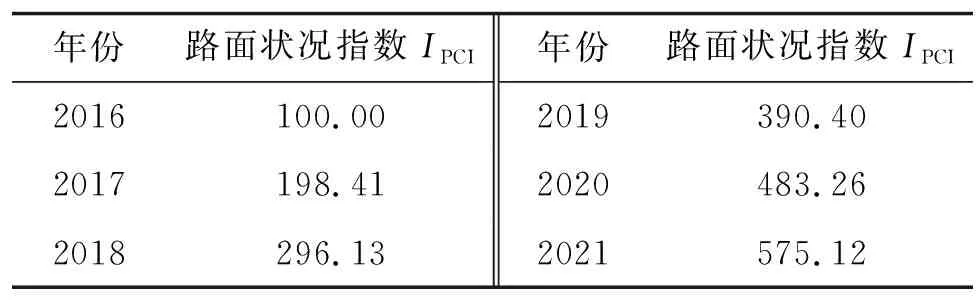
表3 原始檢測數據的累加數據
為保證灰色GM(1,1)模型預測結果的可靠性和穩定性,對原始數據進行可行性分析,包括準光滑性檢驗、準指數檢驗和級比檢驗,公式見式(15)~(17)。滿足以上檢驗標準,即可進行灰色GM(1,1)分析。檢驗結果見表4~6。
(15)
式中:ρ(k)為準光滑性檢驗指標;k=3,4,…,n。
(16)
式中:δ(k)為準指數檢驗指標;k=3,4,…,n。
(17)
式中:σ(k)為級比檢驗指標;k=2,3,…,n。
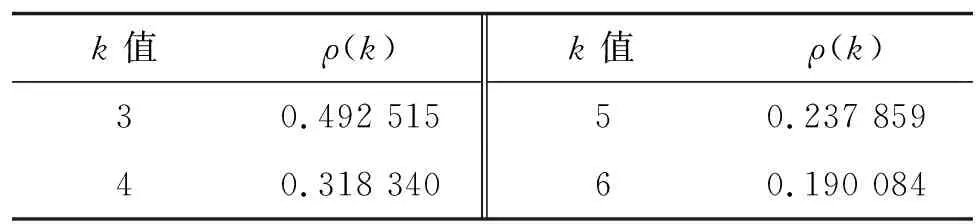
表4 路面狀況指數IPCI的準光滑性檢驗
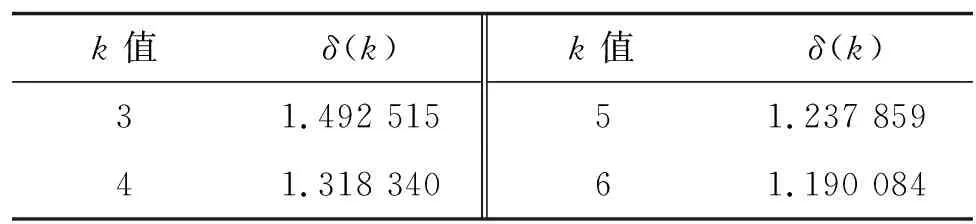
表5 路面狀況指數IPCI的準指數檢驗
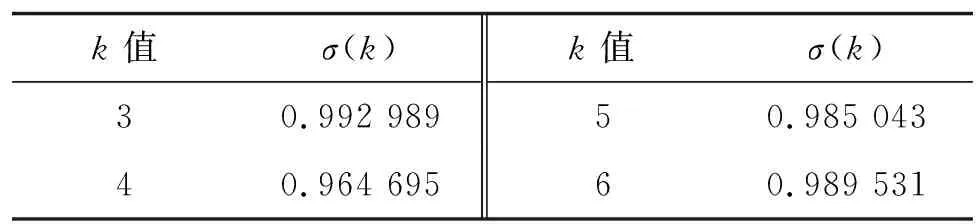
表6 路面狀況指數IPCI的級比檢驗
從表4~6可以看出:采用的原始數據滿足準光滑性檢驗和準指數檢驗要求;σ(k)在(-1.330 7,1.330 7)區間內,滿足級比檢驗要求。根據原始數據建立灰色GM(1,1)模型具有可行性。
2.2.2 建模過程
(1) 生成原始數據的累加序列:
X(1)=(100.00,198.41,296.13,390.40,483.26,
575.12)
(2) 構造矩陣B和向量Yn:
(18)
Yn=(98.41,97.72,94.27,92.86,91.86)T
(19)
(3) 按式(6)求解,得參數a=0.018 925 869、u=101.480 598。
(4) 建立灰色GM(1,1)模型如下:
5 362.005
(5) 按式(7)計算預測值,結果見表7。
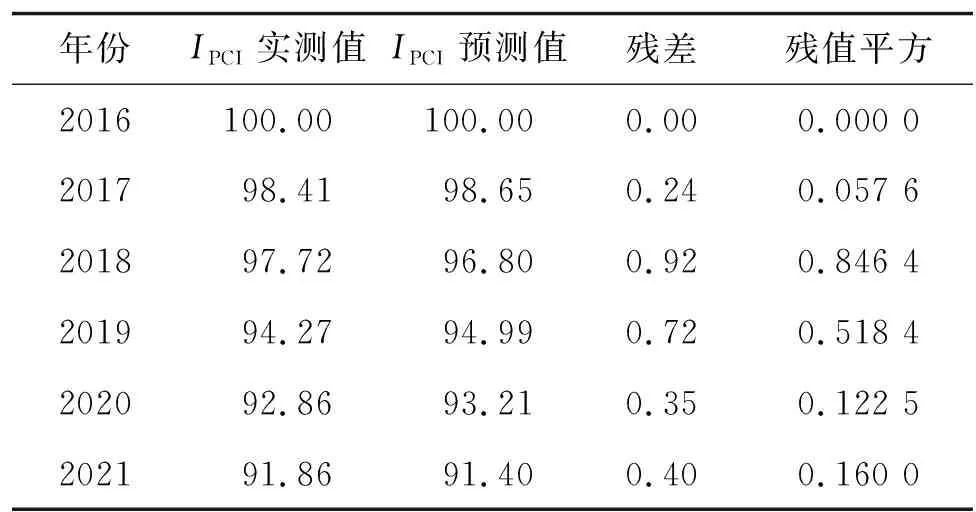
表7 灰色GM(1,1)模型的預測值
(6) 模型精度檢驗。按式(10)、式(11)計算,得C=0.18、P=1。依據表1,模型精度好,符合要求。
2.3 基于灰色馬爾可夫模型的路面狀況指數預測
(1) 根據表7中路面狀況指數IPCI預測值將路面狀況劃分為4種狀態,分別為非常好、好、一般、差(見表8)。

表8 路面狀態劃分
(2) 取4種狀態區間的中值,分別為97.5、92.5、87.5、82.5。
(3) 依據灰色GM(1,1)模型反算達到各狀態區間中值所需時間T,分別為2.76年、5.39年、8.35年、10.65年。以T+1帶入灰色GM(1,1)模型,求出一年后的灰色預測值作為正態分布期望值,分別為95.42、90.79、85.84、82.18。計算路面狀況指數IPCI實測值與預測值的殘差標準差作為正態分布的標準差,為0.58,在所有可能狀態上離散于正態分布。
(4) 計算轉移到各子狀態的概率,以P11計算為例,計算公式見式(20)。同理,計算其他狀態轉移概率,結果見式(21)。
φ(-0.724 14≤x<7.896 552)=0.766
(20)
(21)
(5) 灰色馬爾可夫模型預測。根據2021年路面狀況指數IPCI,路面狀況“好”,則初始向量為(0,1,0,0)。按式(22)計算,得2022年路面狀況指數IPCI預測值為90.36,路面狀況為“好”。同理,計算得2023年、2024年路面狀況指數IPCI預測值分別為89.94、89.54,路面狀況為“一般”。相比于前6年路面狀況指數IPCI實測值的平均衰減速率,2022—2024年的路面狀況指數IPCI預測值的平均衰減速率降低50%。
(22)
路面狀況指數IPCI衰減趨勢見圖1。由圖1可知:復合式瀝青路面路面狀況指數IPCI衰減曲線大致呈反S形。
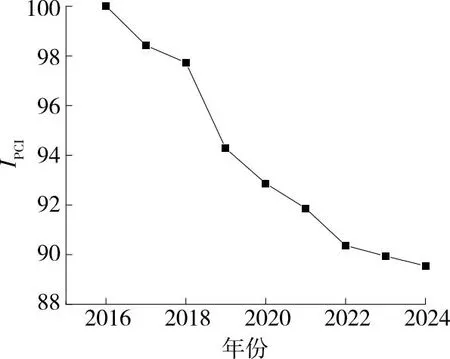
圖1 復合式瀝青路面路面狀況指數IPCI衰減曲線
3 結語
本文采用灰色馬爾可夫模型對潭邵高速公路K1054+000—K1100+500路段復合式瀝青路面路面狀況指數IPCI進行預測,得出2022年、2023年、2024年的預測值分別為90.36、89.94、89.54,復合式瀝青路面衰減曲線大致呈反S形。灰色馬爾可夫模型可以在較少數據的情況下進行建模且建模簡便,實用性強,便于工程應用分析,可為道路科學養護決策提供一定技術支持。

