一道高考線段比值問題的一般化推廣

福建省廈門第一中學(xué) (361003) 陳 恬

1.試題解析

2022年全國(guó)甲卷數(shù)學(xué)第16題考查解三角形、函數(shù)最值等內(nèi)容,考查直觀想象、數(shù)學(xué)運(yùn)算、邏輯推理等核心素養(yǎng).

圖1

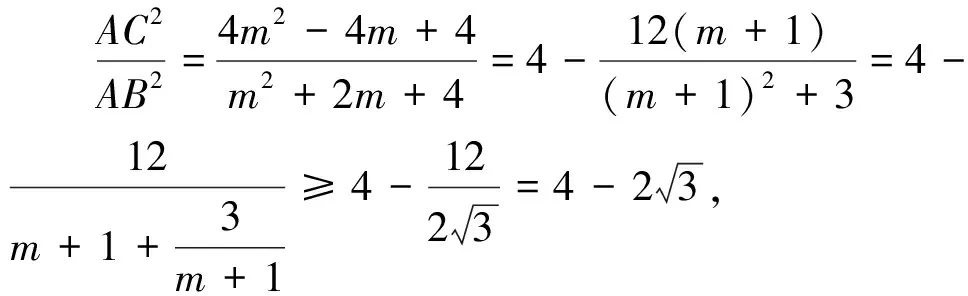
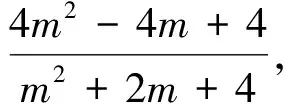
2.試題轉(zhuǎn)化

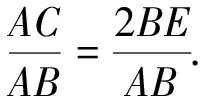
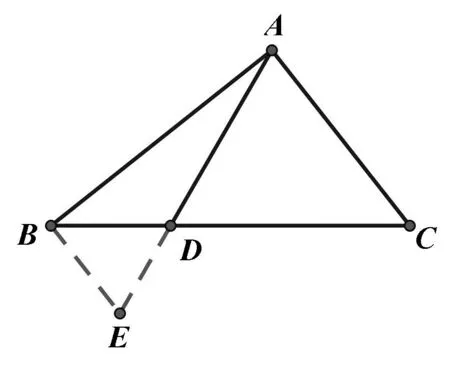
圖2

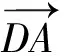
圖3

注意到此處要對(duì)2x-1的符號(hào)進(jìn)行討論:

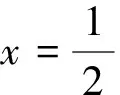
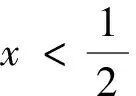
圖4

這個(gè)結(jié)論非常優(yōu)美,幾何構(gòu)造也非常簡(jiǎn)單,從直觀上很容易想到背后可能存在更一般化的幾何性質(zhì).進(jìn)而思考當(dāng)線段的比值改變或夾角改變的情況下,結(jié)論是否成立.

3.一般化推廣

3.1 推廣結(jié)論的驗(yàn)證

分析：由于給出的條件是一般化的,結(jié)論是否成立還不確定,想要從平面幾何直接處理是有難度的,采用解析幾何運(yùn)算來定量分析;又考慮到需要找到點(diǎn)A的位置,因此借助直線參數(shù)方程來解決.

解析：如圖5,以D為原點(diǎn),以BC為x軸,建立平面直角坐標(biāo)系.設(shè)B(-m,0),C(n,0).先考慮特殊情況:

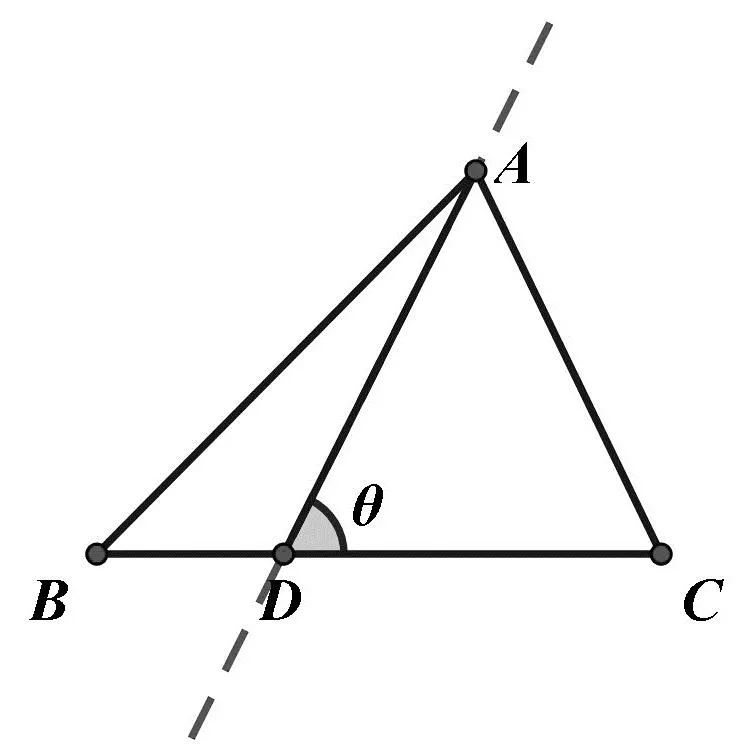
圖5

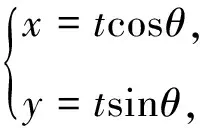
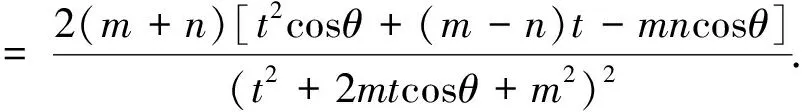
結(jié)合參數(shù)方程的幾何意義,進(jìn)而探究t1,t2的具體涵義.

我國(guó)歷史上最大的一部大型叢書是乾隆三十七年（1772年）下詔纂修的《欽定四庫(kù)全書》。《四庫(kù)全書》編成后，共抄寫七部，分別建立七座藏書樓進(jìn)行收藏，總稱為“四庫(kù)七閣”。 其中，紫禁城的文淵閣、奉天故宮（今沈陽(yáng)）的文溯閣、圓明園的文源閣、承德避暑山莊的文津閣被稱為“內(nèi)廷四閣”。 鎮(zhèn)江金山寺的文宗閣、江都大觀堂（今揚(yáng)州市）的文匯閣和杭州西湖行宮的文瀾閣，被稱為“江浙三閣”。

推廣結(jié)論如圖6,在△ABC中,已知邊BC上一點(diǎn)D,BD=m,CD=n,∠ADB=θ,其中m≠n且0°<θ<180°.則

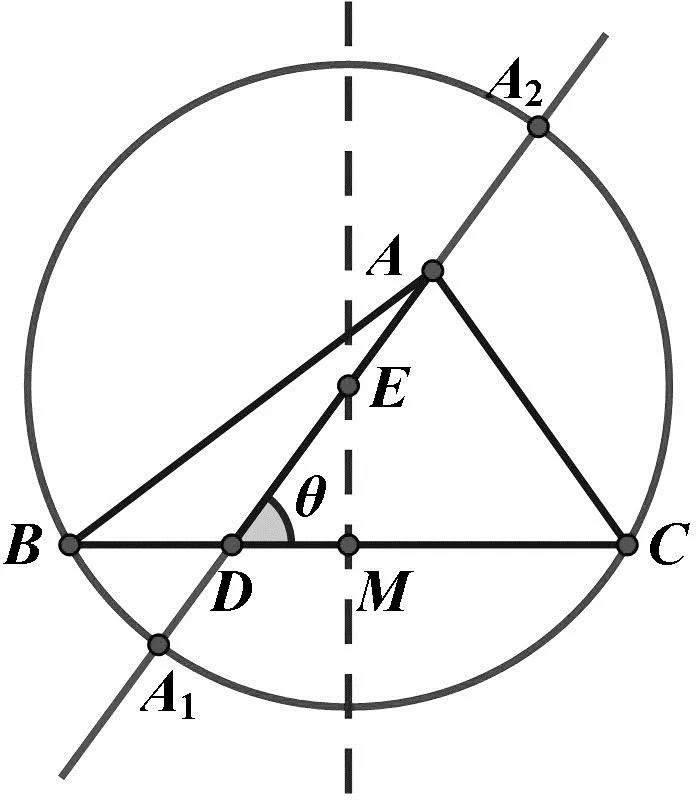
圖6

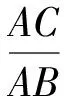
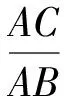
當(dāng)然,可以將θ為直角時(shí)的情況看作圓心E在無窮遠(yuǎn)處,半徑為無窮大,則A1對(duì)應(yīng)是D點(diǎn),A2對(duì)應(yīng)無窮遠(yuǎn)點(diǎn)處.

3.2 推廣結(jié)論的平幾探索

上述方法雖然能夠準(zhǔn)確得到取值的變化規(guī)律,但對(duì)于只求最值的問題來說相對(duì)復(fù)雜.在得到結(jié)論的基礎(chǔ)上,嘗試用平面幾何方法找出最值位置.

圖7

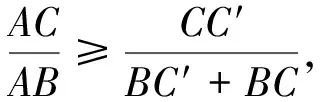
圖8

同理可得當(dāng)θ為鈍角時(shí)的情況.

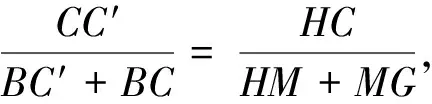
4 結(jié)語

直觀想象核心素養(yǎng)是高考考查的重要內(nèi)容,幾何中的最值問題往往存在一個(gè)更一般化的幾何性質(zhì)作為命題背景,教師與學(xué)生在日常教學(xué)中不應(yīng)只停留在解出問題的表面,還應(yīng)該鼓勵(lì)師生進(jìn)行深入探索,培養(yǎng)堅(jiān)忍不拔的探索精神,形成做研究的習(xí)慣,促進(jìn)數(shù)學(xué)學(xué)科素養(yǎng)的提升.