月面巡視器太陽能帆板功率衰減特性研究
可榮碩,鮑 碩,韓紹金,王曉雪,滕周勇,許 倩
(北京航天飛行控制中心,北京 100094)
0 引言
太陽能帆板是航天器能源系統的重要組成部分[1-2],其光電轉換效率受太陽入射角、太陽距離、遮擋、空間環境、太陽能帆板溫度等諸多因素影響。太陽能帆板的發電性能衰減一直是航天器在軌長期管理關注的重點[3-12]。特別對于“玉兔二號”等承擔地外天體表面巡視勘察的探測器[13],它們自身姿態受天體的表面地形影響,太陽能帆板轉動角度受活動機構約束。每次感知、移動、探測、數傳、出測控弧段和休眠喚醒都必須考慮太陽能帆板的功率輸出情況,以對未來的能源情況進行有效預估。因此太陽能帆板的功率衰減特性分析成為此類航天器必須特別關注的問題[14-20]。本文以“玉兔二號”巡視器為例,分析其自落月來近一年的功率衰減特性,以期為后續深空探測器能源分析和在軌長期管理提供參考。
1 太陽能帆板功率基本原理
根據太陽能帆板發電機理[21-22],太陽能帆板電壓為恒定值,功率衰減特性分析即對太陽能帆板電流進行分析。太陽能帆板輸出電流:
式中:S為帆板面積,m2;Ki為太陽能電池的電流轉換系數,其與太陽能電池溫度、性能衰減、表面灰塵等因素有關;i0為太陽常數,即垂直平面上,單位時間、單位面積內所接收的太陽輻射能量值,其與太陽相對距離平方成反比。
由式(1)可知太陽能帆板輸出電流與太陽能帆板面積、太陽與天體距離、太陽和帆板入射夾角密切相關。在研究功率特性時,為了避免不可控因素的影響,先結合發電原理對不可控因素可能造成的誤差進行分析;然后再對遙測數據進行篩選以盡可能消除誤差;最后對電流遙測進行日月距離和太陽入射角的歸一化,對處理后的數據進行分析,可以得到太陽能帆板的功率衰減規律。考慮理論研究通用性,試驗數據均用標稱單位表示。
2 電流誤差影響因素與數據處理原則
2.1 姿態誤差
由于探測器器上姿態測量設備存在誤差。姿態誤差會引起太陽入射角的計算誤差,月球車太陽能帆板的太陽入射角為60°~40°,入射角每變化1°,太陽能帆板輸出電流變化0.1I0,對應功率變化2~3P0,I0為單位電流,P0為單位功率。
為了消除姿態測量引起的誤差,選取了月午遙測數據,巡視器月午期間處于靜態定姿模式且基本處于同一姿態。
2.2 電流非線性誤差
器上太陽能帆板輸出電流遙測精度為0.07I0,實際輸出電流在2 個分程值之間頻繁跳動,以單日“玉兔二號”帆板輸出電流為例,如圖1 所示。
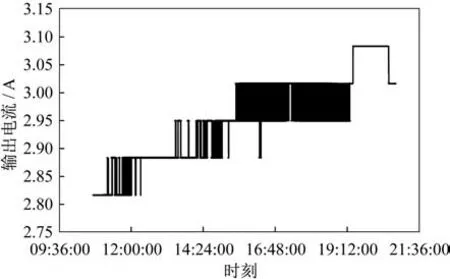
圖1 太陽能帆板電流變化Fig.1 Change of the solar panel current
為避免電流遙測精度內非線性變化帶來的誤差,在選取電流對應參數時,采用滯環方法,即隨著太陽入射角逐漸減小,太陽能帆板輸出電流逐漸增大,從I-0.7I0跳變為I并穩定時,記錄當前入射角記為λin。同理,隨著太陽入射角逐漸增大,太陽能帆板輸出電流逐漸減小,從I+0.7I0跳變為I并穩定時,記錄入射角記為λout,兩次入射角作為輸出電流為I的入射角,稱λin、λout為I的特征點,對應的時刻為特征時刻,如圖2 所示。
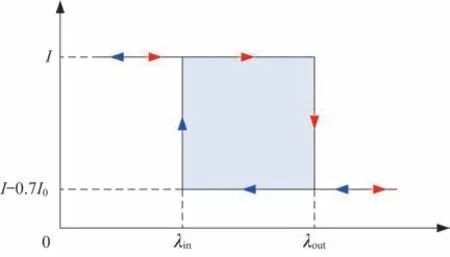
圖2 滯環方法Fig.2 Diagram of the hysteresis loop method
2.3 遮擋因素影響
考慮巡視器桅桿和云臺安裝高度高于太陽能帆板,為了防止桅桿及云臺投影遮擋太陽能帆板,造成太陽能帆板面積不一致,僅對朝向太陽一側的+Y太陽能帆板電流數據進行功率分析。
2.4 測控弧度限制
由于觀測弧度的限制,太陽帆板電流遙測數據有限且不連續。一方面,間斷且有限的遙測數據使得太陽能帆板的功率分析不能涵蓋連續的太陽入射角;另一方面,在利用滯環方法處理時,弧度結束前的短時間數據不能判斷電流I是否穩定,會造成λin、λout特征時刻的誤差。為此,在處理數據時選取共10 個月晝的數據進行分析,并且去除了測控弧度結束前1 h 的特征數據。
2.5 溫度影響
根據歷次月晝月午期間溫度遙測變化橫向比對,相同入射角條件下,帆板溫度相差小于5°,且無明顯規律,研究的電流數據所對應的太陽能帆板溫度差異較小,不考慮溫度差異對輸出電流的影響。
3 電流數據處理方法及分析
3.1 滯環方法處理遙測
為了避免電流遙測精度內非線性帶來的誤差,采用滯環的方法對遙測數據進行初步處理,首先根據遙測下傳時間利用JPL DE430 星歷計算巡視器當地太陽高度角、方位角;然后根據姿態和太陽能帆板展開角度換算成太陽入射角,其中垂直入射角度為0°。
滯環方法處理太陽入射角逐漸減小的遙測數據算法偽代碼見表1,其中太陽入射角逐漸增大的算法同理可得,算法的核心就是分成太陽入射角逐漸減小和逐漸增大兩個部分,在每個部分中找到每個電流分層值最后出現的時刻,在電流穩定進入下一個電流分層值時刻對應的入射角就是λin或者λout。

表1 滯環方法處理遙測Tab.1 Process of telemetry by the hysteresis loop method
根據上述算法處理出的有效數據如圖3 所示。
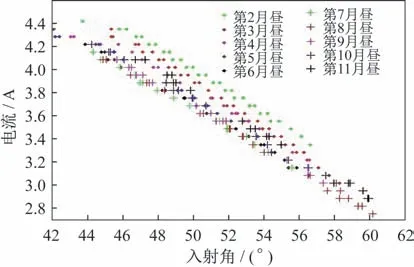
圖3 太陽能帆板電流與入射角的關系Fig.3 Relation between the solar panel current and the incident angle
整體上分析:1)隨著太陽入射角的逐漸增大電流值逐漸減小;2)太陽入射角在44°~60°范圍內,太陽能帆板輸出電流值在2.8I0~4.4I0變化;3)隨著“玉兔二號”在軌運行,同一太陽入射角下,太陽能帆板輸出電流值逐漸減小;4)由圖3 可知,第6、7 月晝電流值偏小,主要原因是日月距離在6、7 月份達到最大,電流值受日月距離影響,因此在本文第二小節進行了日月距離的歸一化處理。
3.2 距離歸一化
根據文獻[23],光照強度與月日距離平方成反比,并在試驗中得到了驗證。日月距離變化范圍在1.47 億~1.52 億km,距離的變化對于輸出電流影響最大約為9%,因此僅考慮輸出電流(功率)與入射角的關系,不能準確描述其發電能力。對電流I進行距離的歸一化,換算成同一距離R0=1.47×108km 得到歸一化電流I′。計算公式為
式中:I為原始電流值,A;r為對應的日月距離,km。
距離歸一化的結果如圖4 所示。
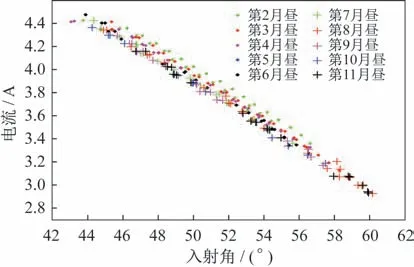
圖4 距離歸一化的電流與太陽能帆板入射角的關系Fig.4 Relation between the solar panel current and the incident angle after distance normalization
結合圖3、圖4 可知,隨著巡視器在軌時間積累,相同太陽入射角,同一距離下,太陽能帆板電流值逐漸減小,太陽能帆板功率逐漸衰減,從第2 月晝到第11 月晝電流值減少約0.2I0。
3.3 太陽入射角歸一化
進一步根據式(1)可知,太陽能帆板的電流值與太陽入射角的余弦值成正比關系,為了在同等條件下分析太陽能帆板的電流值,對電流值I′進行太陽入射角的歸一化得到I′。
式中:θ0=0°,即換算成太陽垂直入射時的電流值。
入射角歸一化得到的電流數據如圖5 所示,分析可得:1)理論上太陽入射角歸一化后,每個月晝不同入射角的電流值應基本相等,但是從圖5 可知,電流值在44°~60°入射角下電流值存在一定下降趨勢。根據崔鵬等[24]對“玉兔一號”的入射角效應分析,在大入射角下,實際的功率降低趨勢比余弦值的降低趨勢更為迅速,入射角60°附近與余弦值不一致系數將達到2%,即6I0的電流會存在0.12I0的電流差值,與圖5 的數據基本一致。2)在太陽入射角為44°~60°,整體上看太陽能帆板的功率逐月衰減,前6 個月的衰減趨勢大于后4 個月衰減。3)計算10 個月晝44°~60°電流的平均值,可以得到研究的近1 年巡視器太陽能帆板功率衰減了約2.5%。
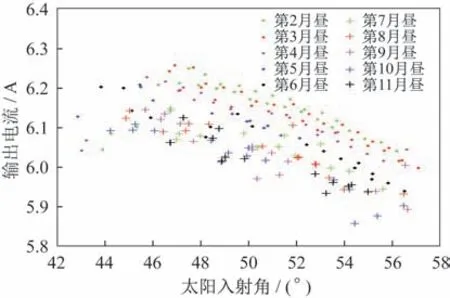
圖5 歸一化入射角之后電流的變化值Fig.5 Current after incident angle normalization
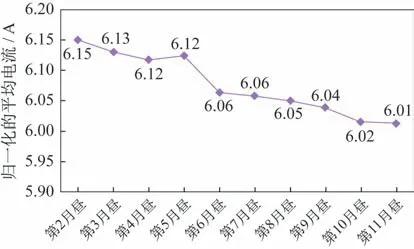
圖6 月晝歸一化后電流平均值Fig.6 Average current after lunar patrol normalization
4 結果驗證
巡視器月夜處于休眠狀態,當帆板發電電流達到喚醒電流時,巡視器自主喚醒,由巡視器喚醒特性可知,喚醒電流為恒定值[25],喚醒常數可以表示為
式中:n為月晝;SK1K2/Iw為喚醒常數;Iw為喚醒時刻電流,A;S為帆板面積,m2;K1為太陽能電池的電流轉換系數;K2為日月平均距離下的太陽常數。月晝喚醒常數及日月距離如圖7 所示。
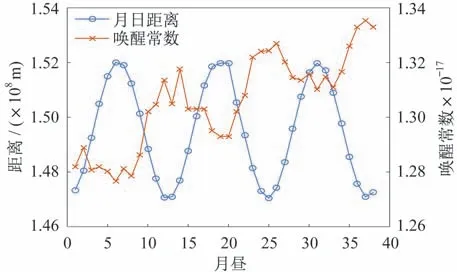
圖7 歷次喚醒常數統計Fig.7 Statistics of successive wake-up constants
由于在大入射角情況下太陽能帆板發電特性與入射角不是標準余弦關系,為減少入射角帶來的誤差,取第2 及13 月晝2 次月日距離相近的喚醒常數樣本,2 次常數的比值可以近似表示發電性能的衰減情況。計算得出衰減率為2.7%,與上述分析結論基本一致。
5 結束語
本文對地外天體巡視器的帆板功率衰減特性進行分析,針對系數遙測首先利用一種滯環的方法對大量的電流遙測進行數據處理;然后進行日月距離和太陽入射角的歸一化處理;最后擬合數據計算太陽能帆板的功率衰減。結果表明,巡視器近1 年來發電功率共衰減了2.5%,利用巡視器晝喚醒時刻的太陽入射角變化情況對衰減特性進行驗證可為后續巡視器長期管理提供參考。

