一種基于航跡特征的無人機與飛鳥目標雷達識別方法

管康萍，馮正康，馬小艷，張良俊，崔 杰，葉 舟

（1.中國人民解放軍93128 部隊，北京 100080；2.上海航天電子通訊設備研究所，上海 201109）

0 引言

隨著無人機（Unmanned Aerial Vehicle，UAV）領域技術的快速發展，因其具有成本低、體積小、操作簡單等優勢，已經廣泛應用于軍事和民用領域。但隨著非合作無人機黑飛、干擾等事件的頻發，已經成為一項重要隱患，而且在航空器起飛或飛行的過程中與鳥類相撞的事件也層出不窮，飛鳥的防范壓力也越來越大，這兩類目標都對機場、安保等重要場所產生嚴重的威脅［1-9］。一般根據不同的作戰環境要求，針對這兩者類型目標，在發現后需要采取不同的反制手段和措施，如機場一般在發現飛鳥后，會采取驅鳥設備將其驅趕，而對無人機目標則會采取預警、協調等措施，因此對無人機和飛鳥的識別極其必要。

目前，對無人機和飛鳥的監視和識別方法主要分為兩類，一類從目標回波特性角度出發，由于無人機多旋翼轉動與飛鳥翅膀扇動產生的回波信號存在特性差異，所以一般采用時頻分析算法提取兩者的微多普勒特征。法國航天航空研究中心采用DVB-T 信號進行了多旋翼無人機微多普勒測量實驗，荷蘭Robin公司雷達則采用發射調頻連續波形，同時具備無人機探測和識別的功能。在隨后多年發展中，國內外單位通過設計優化雷達工作系統、工作模式、發射接收波形、延長駐留時間等方法來進一步提取精細化特征，但實際應用到復雜多變的環境中，目前還是較為困難，尤其當目標處于遠距離時，兩者的回波特征微弱導致特征提取困難、時頻分辨力低等，限制了大范圍的應用與發展［10-15］。另一類方法則是從無人機與飛鳥的飛行軌跡特征方面出發，通過記錄大量歷史數據，熟悉了解飛鳥的活動規律和飛行軌跡，從數據層提取無人機與飛鳥的運動軌跡特征。目前采用多運動模型并通過計算模型間轉換頻率的方法來進行識別，也有利用航跡軌跡信息建立特征量并利用機器學習或深度學習的方法［16-22］來進行識別，這幾種方法都進一步驗證了該類方法的可行性。

本文提出的無人機與飛鳥目標雷達識別方法，與現有識別方法的不同點在于：1）未采用復雜的時頻分析方法，而是采用輕量性的航跡數據集，較大降低了雷達系統的識別成本，普適性強；2）為了更好地體現兩者飛行軌跡上的特征差異，采用支持向量機（Support Vector Machines，SVM）算法模型，提出時間相關的航向、速度震蕩頻率特征向量描述方法，并結合其他特征量，實現在線動態修正并預測，能夠更好地提高識別準確率。

1 特征分析

無人機與飛鳥目標雷達識別流程如圖1 所示，首先基于歷史雷達系統航跡數據分析和研究無人機與飛鳥在運動軌跡上的特征差異，提出以航跡層信息為基礎，建立航向角標準差、航向震蕩頻率、速度均值、速度標準差、速度震蕩頻率這5 個特征量。其次將模塊劃分為離線訓練和在線處理部分，離線訓練下將歷史樣本分為訓練、測試樣本，對訓練樣本采用支持向量機算法交叉訓練獲得最優超參數，并利用測試樣本驗證識別準確率。在線狀態下利用最優參數，根據雷達穩跟目標航跡實時計算特征量，利用預測模塊算法進行判別輸出。

圖1 無人機與飛鳥目標識別框Fig.1 Block diagram of UAV and bird target recognition

1.1 特征描述

從無人機與鳥類的活動軌跡來描述，一般飛鳥的飛行軌跡相對靈活且時間較短，而典型無人機作業一般是按照預先設定的航線任務飛行，通常分為連續直線飛行、航點懸停、折返飛行、多方位多點飛行等路線。因此該類無人機目標的飛行軌跡時間較長，且一般相對穩定，但如果是人工干預控制操作飛行，其在轉向、折返、懸停上則具有較高的自由度，將連續人工干預操作無人機機動飛行稱為強機動模式，按照航點任務作業稱為弱機動模式。

利用具備探測跟蹤無人機和飛鳥功能的某相控陣雷達系統平臺，通過大量實驗工作與歷史航跡數據記錄分析，典型的無人機和鳥類在航跡層級別的飛行軌跡如圖2、圖3 所示。從距離、方位角、航跡長度可以直觀體現出兩者的區別，完善數據庫，其中無人機航跡數據層中包含了大量無人機不同作業類型的航跡，例如手動操作、直線、8 字、折返、懸停飛行等不同軌跡。下面從運動軌跡的局部和總體特征分別描述無人機與飛鳥的特征量的差異，這些特征量分別是航向角標準差、航向震蕩頻率、平均速度、速度標準差、速度震蕩頻率。

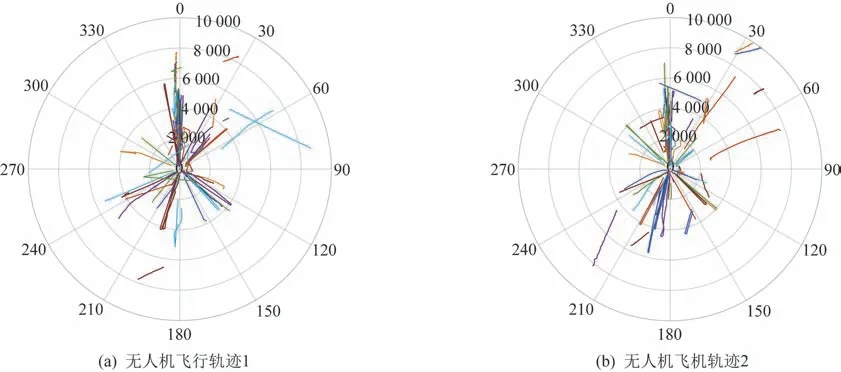
圖2 典型無人機飛行軌跡Fig.2 Typical flight trajectories of UAVs

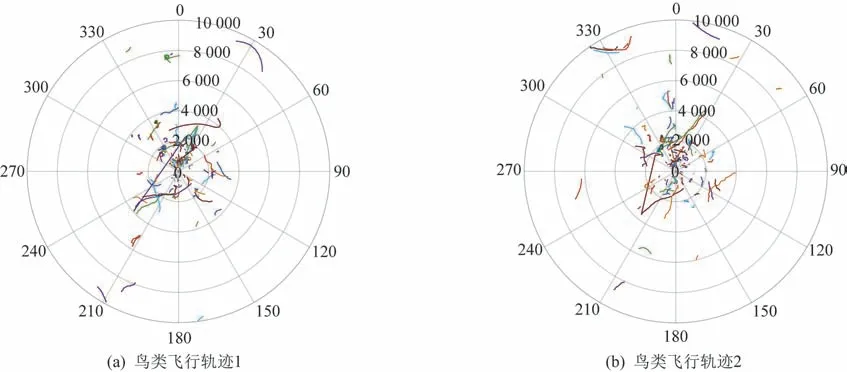
圖3 典型鳥類飛行軌跡Fig.3 Typical flight trajectories of birds

航向角標準差：對于一般飛鳥的軌跡，其方向性相對比較隨機，標準差變化范圍較大，而無人機在執行弱機動模式飛行時，其標準差值較小。對于這類可以通過對比航向角標準差的差異，較明顯地體現出兩者飛行軌跡的區別，而在強機動模式下時取值范圍較大，較難區分。

航向震蕩頻率：上述航向角標準差只能體現兩者的總體特征，并不能較好地描述局部航向變化特征。為此引入航向震蕩頻率表征兩者的區別，無人機在弱機動模式下其航向震蕩次頻率值較小，而在飛行過程中，如果只是部分時間人工干預控制操作讓其處于強機動模式飛行，隨著跟蹤次數增加，航向震蕩頻率值也會逐漸變小，但如果是一直處于強機動模式飛行，則航向震蕩頻率值一直處于較高的值。因此對于無人機，其航向震蕩頻率值總是處于較大或者較小值，而飛鳥的飛行軌跡較為靈活且相對平滑，加上一般雷達對其跟蹤時間較短，其航向震蕩頻率數值處于較小與較大范圍之間，所以航向震蕩頻率具備區分無人機與飛鳥的潛力。

平均速度：其對于區分飛鳥和低速無人機不太明顯，但是仍然可以作為區分一些大型無人機和飛鳥目標的特征，例如一般固定翼無人機的飛行速度遠超于飛鳥。

速度標準差：對于飛鳥而言，其速度相對比較穩定，其標準差的數值一般較小，而無人機由于其飛行相對自由，例如懸停、加速、減速等機動都會影響飛行速度，因此在其機動過程中標準差的數值相對較大，能夠作為區分無人機與飛鳥的一個特征。

速度震蕩頻率：對于飛鳥而言，其速度不會產生突變的情況，而在無人機轉向飛行或者懸停過程中，需要加速或者減速。上述速度標準差只能體現兩者的總體特征，并不能較好地描述局部速度變化特征，為此引入速度震蕩頻率來體現速度局部變化特征。一般飛鳥的速度震蕩頻率數值很小，而無人機在加速或減速過程中，雖然只需要較短的時間，但此時的速度震蕩頻率值相對較大。因此通過長時間積累，可以作為區分飛鳥與強機動模式下無人機的飛行特征。

1.2 特征計算

定義某條長度為N的航跡目標集合符號記為S={s(1)，s(2)，…，s(N)}，每個數據采樣點記為符號s，其中第i個航跡采樣點s(i)={r(i)，θ(i)，φ(i)，[v(i)]分別代表目標在該時刻的距離、方位角、俯仰角和速度。

1）航向角標準差

為方便計算航向角，將航跡數據集合下每個采樣點s(i)的距離、方位、俯仰(r(i)，θ(i)，φ(i))轉化為直角坐標系下(x(i)，y(i)，z(i))，轉換公式為

根據上一時刻s(i-1)和當前時刻s(i)算出直角坐標系下的位置信息x(i-1)、y(i-1)、x(i)、y(i)、計算當前i時刻的航向角，符號記為h(i)，計算公式為

其中，計算航向角時需考慮x(i)-x(i-1)、y(i)-y(i-1)值所處的象限區域，從而將-90°～90°的值域轉化為0°～360°，則航跡集合S航向角集合H為

要計算航向角的標準差，首先要計算航向角的均值，但是存在某些目標軌跡的航向角跨0°、360°或由于受測量角度誤差的影響，而導致產生的跨越情況，因此對于航向角不能采用常規均值方法計算。采用向量化的方法描述這類周期性角度的數據［23］，計算周期性數據均值與標準差的方法是首先將第i個航向角h(i)轉化為二維平面上的單位向量r(i)，該航向角在x軸坐標值對應于cosh(i)，y軸坐標值對應于sinh(i)，公式為

把H集合中N-1 個航向角轉換成矢量并且相加得到合成向量rs，計算公式如下，航向角均值hm和標準差hstd分別定義為

其中，航向角均值需要考慮rs所處的象限區域，將航向角均值轉化為0°～360°。

2）航向震蕩頻率

為了反映航向變化局部特征，引入航向震蕩頻率，首先對航跡目標集合S之間的相鄰航向角計算差值，記為符號dh(i)，公式為

并判斷角度差dh(i)與設定閾值γh之間的大小，計算出航向角之間的差異符號值O(i)，定義為

根據航向角符號值集合O正負符號變換關系，定義兩種航向震蕩模式［24］：

當滿足上述式（10）或式（11）時，判定處于震蕩模式并統計震蕩次數，符號記為Uh：

式中：γh為航向角差異判定的閾值，可以根據實際雷達測角誤差設定。

在得出航向震蕩次數后，定義航向震蕩頻率為

3）平均速度

航跡目標集合S的平均速度計算公式為

4）速度標準差

航跡目標集合S的速度標準差計算公式為

5）速度震蕩頻率

為了反映速度變化局部特征，引入速度震蕩頻率，在當前時刻i，取歷史L長度段樣本點的速度值，計算該長度下的速度均值vmL，定義為

計算當前點速度v(i)和歷史均值速度vmL之間的差值，符號記為τv(i)，定義為

設定速度變化閾值γv，當差值大于γv，則該點定義為速度震蕩，符號記為Uv(i)，定義為

其中，可根據實際雷達跟蹤數據率、跟蹤精度調整閾值γv和L長度，速度震蕩頻率定義為

最后得出航跡計算特征量為航向角標準差、航向震蕩頻率、速度均值、速度標準差、速度震蕩頻率，符號為G=[hstd，fh，vm，vstd，fv]，利用這5 個特征量可能在跟蹤開始階段誤判目標的類型，但隨著目標穩定跟蹤時間和次數的增加，時間相關的特征量值可以通過在線動態修正并重新對目標類型進行預測，識別的準確率也會逐步提高。

1.3 離線訓練與測試

1）模型選擇

在上述得到5 個特征量后，考慮樣本特征量非線性且為了防止過擬合，采用軟間隔的支持向量機算法［25］，其模型公式為

式中：w為超平面法向量；C為常數，且大于0；ξ為松弛變量；?(x)為映射函數；b為超平面的截距；xi為樣本矢量。

上式計算會引入核函數κ(xi，xj)，本文采用高斯核函數，公式為

式中：σ為高斯核函數的帶寬，后續采用序列最小優化（Sequential Minimal Optimization，SMO）算法求解模型。

2）訓練模型與驗證

在確定支持向量機模型后，不同大小的超參數對識別的準確性有較明顯的影響。在高斯核函數中需要調整的超參數是懲罰因子C和核函數的帶寬σ，首先利用隨機采樣法將航跡數據集分為訓練和測試樣本集，然后將訓練樣本數據集采用5折交叉訓練法，尋得最優超參數。獲得訓練模型和最優超參數后，再利用測試樣本集對模型進行驗證評估。其中測試樣本集數中無人機和鳥類航跡數量分別為114 和76 條，識別混淆矩陣見表1，其中準確識別率為87%，驗證了該方法的有效性。

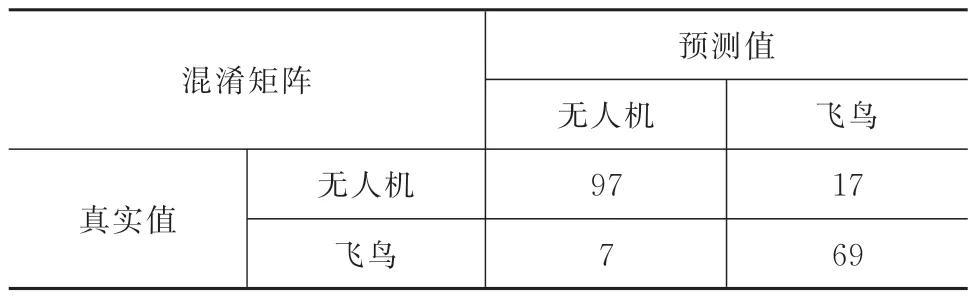
表1 識別混淆矩陣Tab.1 Identification confusion matrix

1.4 識別結果分析

通過對上述誤識別的無人機和飛鳥樣本進行分析，發現簡單平滑且軌跡持續較長的飛鳥與弱機動模式下無人機的特征相差較小，目前仍難以區分。后續為了進一步提高識別率，需要完善飛鳥數據庫樣本，更加仔細地提取與無人機的差異，如通過回波強度區分，通過某些地理區域內鳥類的活動節律進行統計，從而輔助提高決策的準確率。

2 實驗驗證

實驗過程中以某相控陣雷達系統為平臺，部署在飛鳥較為活躍的山林環境。無人機型號為大疆精靈4，考慮到實驗的完整性，無人機模擬了多次不同作業和人工操作飛行場景的任務，其中在某次跟飛實驗中，雷達目標跟蹤與識別的平面顯示器（Pixel Per Inch，PPI）畫面，如圖4、圖5 所示，圖中符號R、A、E、V、H分表代表距離、方位角、俯仰角、速度、高度。

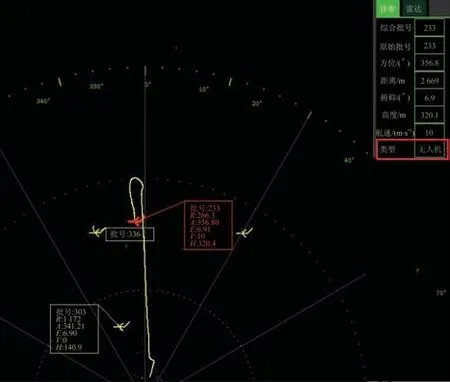
圖4 無人機目標跟蹤識別PPIFig.4 Tracking recognition PPI diagram for UAV targets

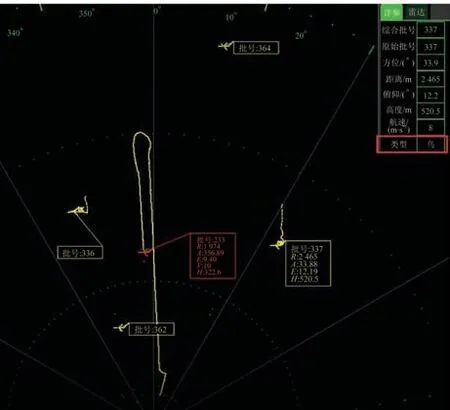
圖5 飛鳥目標跟蹤識別PPIFig.5 Tracking recognition PPI diagram for bird targets

由圖4、圖5 可見，無人機目標的批號為223，方位角在356°方向，運動軌跡為首先經過一段背離雷達方向的飛行，在到達指定航向任務點時拐彎調轉方向，并按照進入雷達的方向飛行，而飛鳥目標的批號為337，方位角在33°方向，飛行軌跡較為無序，雷達在穩定持續跟蹤情況下，均正確識別了無人機與飛鳥目標，實驗結果驗證了該方法在工程角度實現的輕量性與可行性。

3 結束語

本文分析了無人機與飛鳥在運動軌跡上的特征差異，基于大量歷史雷達探測航跡數據分析，提出了時間相關的航向、速度震蕩頻率特征量計算方法，并將機器學習領域的SVM 算法應用到實際雷達跟蹤識別處理中，通過離線和在線均驗證了識別分類的有效性和準確率，在工程角度上具有輕量性、實用性、適用性。