《反比例函數(shù)的圖象與性質(zhì)》課件設(shè)計

黃棟

特色與亮點

①課件利用幾何畫板取點，快速計算出對應(yīng)的函數(shù)值，并準確描點。這樣既能彌補學生動手畫圖時描點的不足，又能節(jié)約大量的時間。

②課件利用迭代法實現(xiàn)大量取點，無數(shù)個點合在一起，就形成了反比例函數(shù)的圖象。超大量的取點可以在視覺上給學生以沖擊，使學生正確認識反比例函數(shù)的圖象，并初步體會函數(shù)的可微性。

③課件通過圖形的動態(tài)演示，讓學生明白矩形的長與寬之間是一個連續(xù)的、平滑的變化過程，所以形成的曲線是光滑的曲線；整個滑動變化過程讓學生感受到函數(shù)圖象的連續(xù)性。

④課件以微視頻的形式呈現(xiàn)幾何畫板作圖，既解決了本節(jié)課的難點，又節(jié)約了大量的時間，并且此微課還可以在課后的復(fù)習中觀看學習。

制作背景

反比例函數(shù)是一種反映現(xiàn)實世界中數(shù)量關(guān)系的模型，在各領(lǐng)域應(yīng)用比較廣泛。通過反比例函數(shù)的學習，可以讓學生進一步體會各學科之間的聯(lián)系，感受數(shù)形結(jié)合的思想，并為二次函數(shù)的后續(xù)學習奠定基礎(chǔ)。

本章分為三節(jié)課：①通過現(xiàn)實問題，抽象出反比例函數(shù)的概念；②利用描點法，畫出反比例函數(shù)的圖象，研究圖象，得出性質(zhì)；③分析實際問題，建立反比例函數(shù)模型，發(fā)展函數(shù)的應(yīng)用意識。

初二的學生學習了變量之間的關(guān)系和一次函數(shù)，知道畫函數(shù)圖象的一般步驟，能畫出一次函數(shù)的圖象。但是，一次函數(shù)是一條直線，而反比例函數(shù)是雙曲線，原有的經(jīng)驗容易對現(xiàn)在的學習產(chǎn)生負遷移，所以筆者借助幾何畫板來輔助教學。

新課標對本節(jié)課的要求為：能畫出反比例函數(shù)的圖象，根據(jù)圖象和表達式探索并理解反比例函數(shù)的性質(zhì)。其中，正確畫出反比例函數(shù)的圖象是本節(jié)課的重點，而理解反比例函數(shù)的圖象是光滑的雙曲線為本節(jié)課的難點。

設(shè)計思路及內(nèi)容結(jié)構(gòu)

1.設(shè)計思路

①復(fù)習定義：利用路程問題復(fù)習反比例函數(shù)的定義；②回憶作圖：引導(dǎo)學生回憶畫一次函數(shù)圖象的步驟；③自主作圖：鼓勵學生按照自己的理解畫出反比例函數(shù)圖象；④投影討論：投影展示有代表性作品，并交流討論；⑤畫板呈現(xiàn)：幾何畫板迭代法繪制反比例函數(shù)圖象；⑥鞏固練習：根據(jù)所得經(jīng)驗加深對反比例函數(shù)圖象的認識；⑦交流性質(zhì)：比較討論圖象，得出性質(zhì)；⑧典例應(yīng)用：通過練習加深對性質(zhì)的理解；⑨課堂小結(jié)：回憶本節(jié)課所學知識；⑩課堂檢測：檢查本節(jié)課學生的掌握情況。

2.內(nèi)容結(jié)構(gòu)

（1）環(huán)節(jié)一：復(fù)習定義

課件：（出示問題）“如何表示所需時間？t是v的什么函數(shù)？反比例函數(shù)表達式的一般形式是什么？它另外的表現(xiàn)形式如何表示？”然后依次呈現(xiàn)問題答案以及反比例函數(shù)表達式的三種表現(xiàn)形式（如上頁圖1）。

目的：復(fù)習反比例函數(shù)的定義，引出下一步的探究任務(wù)是畫圖象；復(fù)習表達式的三種表現(xiàn)形式，其中xy=k的形式，為后面引入面積不變的矩形做鋪墊。

預(yù)期：在上一節(jié)課，學生已經(jīng)學習了反比例函數(shù)的定義，并且教材是用電學問題、路程問題等現(xiàn)實問題抽象出的反比例函數(shù)概念，所以此路程問題學生很容易解答。

①活動一：回憶作圖。

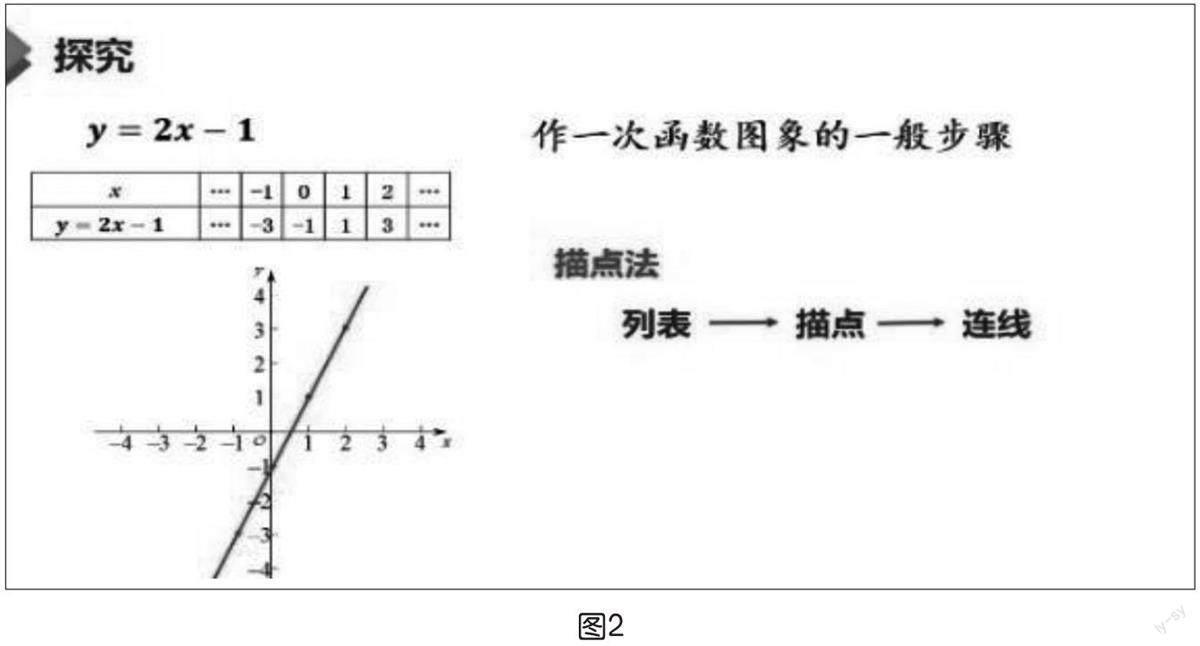
課件：（出示問題）我們?nèi)绾萎嫵鲞@個一次函數(shù)的圖象呢？顯示一次函數(shù)的表達式，點擊課件后依次呈現(xiàn)列表、坐標系中描點、連線；總結(jié)列表、描點、連線這種作圖方法為描點法（如圖2）。

目的：使學生認識到在畫函數(shù)圖象時，描點法是最基本的方法，從而為接下來嘗試畫反比例函數(shù)圖象做準備。

預(yù)期：（出示）畫任何未知函數(shù)圖象的最基本的方法是描點法。

②活動二：自主作圖。

目的：學生在動手畫圖的過程中，對畫函數(shù)圖象有進一步的理解與認識。

預(yù)期：學生對畫函數(shù)圖象的三個步驟的掌握還不夠熟練，所以難免會出現(xiàn)問題。教師關(guān)注作圖過程中出現(xiàn)的典型錯誤，利用投影儀的拍照功能，將有代表性的作品拍照，作為下一個環(huán)節(jié)探討的問題。

③活動三：投影展示。

課件：投影展示有代表性的作品，總結(jié)典型錯誤及應(yīng)對措施。（出示問題）到底該如何連線？

目的：通過投影展示典型問題，讓學生明確畫圖過程中的錯誤是什么原因造成的，該如何應(yīng)對，從而為后續(xù)作圖打下基礎(chǔ)。

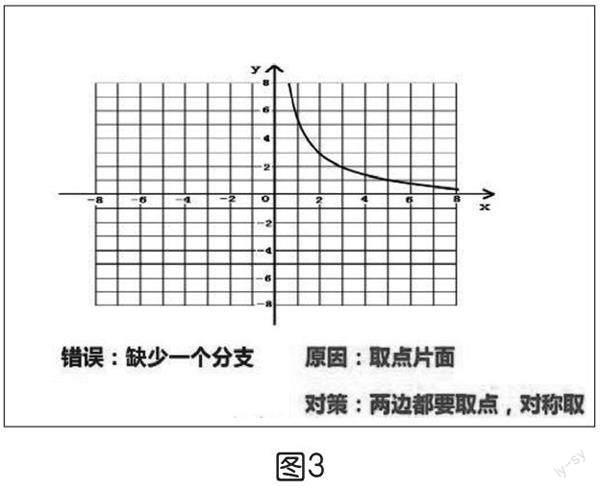
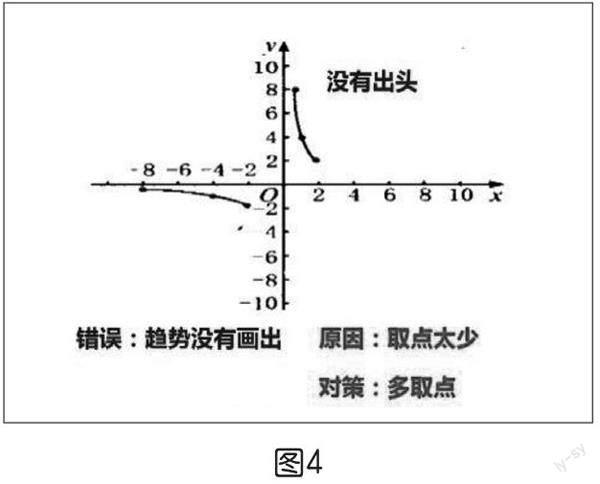
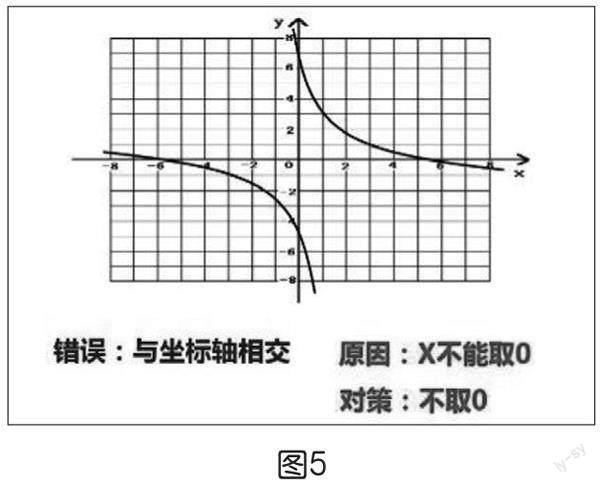
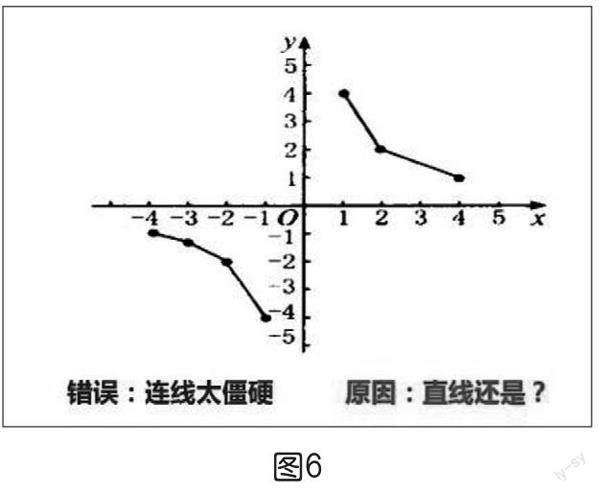
預(yù)期：若學生不會分析判斷，可以用問題的形式引導(dǎo)學生進行分析。（出示課件，如上頁圖3～圖6）圖3的問題是取點片面造成的，解決辦法：兩邊都要取點。圖4的情況是取點過少造成的，解決辦法：多取點。圖5的情況是取值范圍不當造成的，解決辦法：分析為什么不能與坐標軸有交點，明確自變量的取值范圍。圖6中學生可能會對“用光滑的曲線順次連接各點”有疑惑，出示新的問題：這些點之間該如何連線？從而進入下一環(huán)節(jié)。

④活動四：畫板呈現(xiàn)。

課件：視頻播放幾何畫板繪制反比例函數(shù)的圖象。

目的：利用幾何畫板動態(tài)大量取點，彌補手工畫圖象時描點較少的不足，從而讓學生正確認識反比例函數(shù)的圖象。

預(yù)期：在微課中，分析無法正確畫圖原因，逐次增加繪制點數(shù)進行畫圖，通過微課學習，學生能較好地理解并掌握圖象的形狀。

⑤活動五：鞏固練習。

目的：根據(jù)所得經(jīng)驗再次作圖，使學生進一步熟悉反比例函數(shù)的圖象，體會函數(shù)圖象與表達式之間的關(guān)系，感受數(shù)形結(jié)合的思想。

預(yù)期：有了之前的經(jīng)驗，學生在畫新圖象時，基本不會出現(xiàn)典型的問題，用時也會減少。

⑥活動六：交流性質(zhì)。

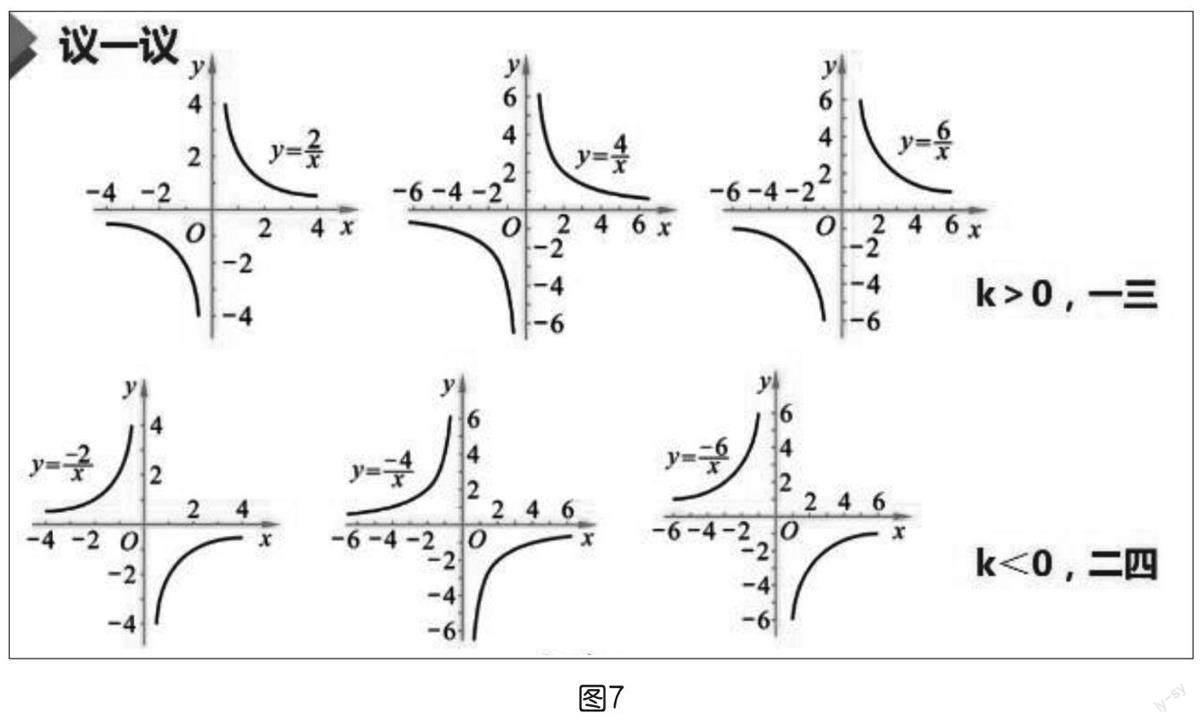
課件：出示多個反比例函數(shù)圖象（如圖7），供學生觀察分析。

目的：通過之前畫圖以及觀察分析，得出k與坐標系之間的關(guān)系。

預(yù)期：由于剛剛經(jīng)歷過畫反比例函數(shù)的圖象，外加在多個圖象的驗證下，學生較容易得出k與坐標系之間的關(guān)系。

⑦活動七：操作教具。

課件：利用教具，探討反比例函數(shù)圖象的中心對稱性與軸對稱性。

目的：通過動手操作，將同桌的圖象釘在一起，探討旋轉(zhuǎn)后圖象的重合情況，得出反比例函數(shù)的中心對稱性；然后折疊所畫圖象，探究圖象與自身重合的情況，得出反比例函數(shù)的軸對稱性。

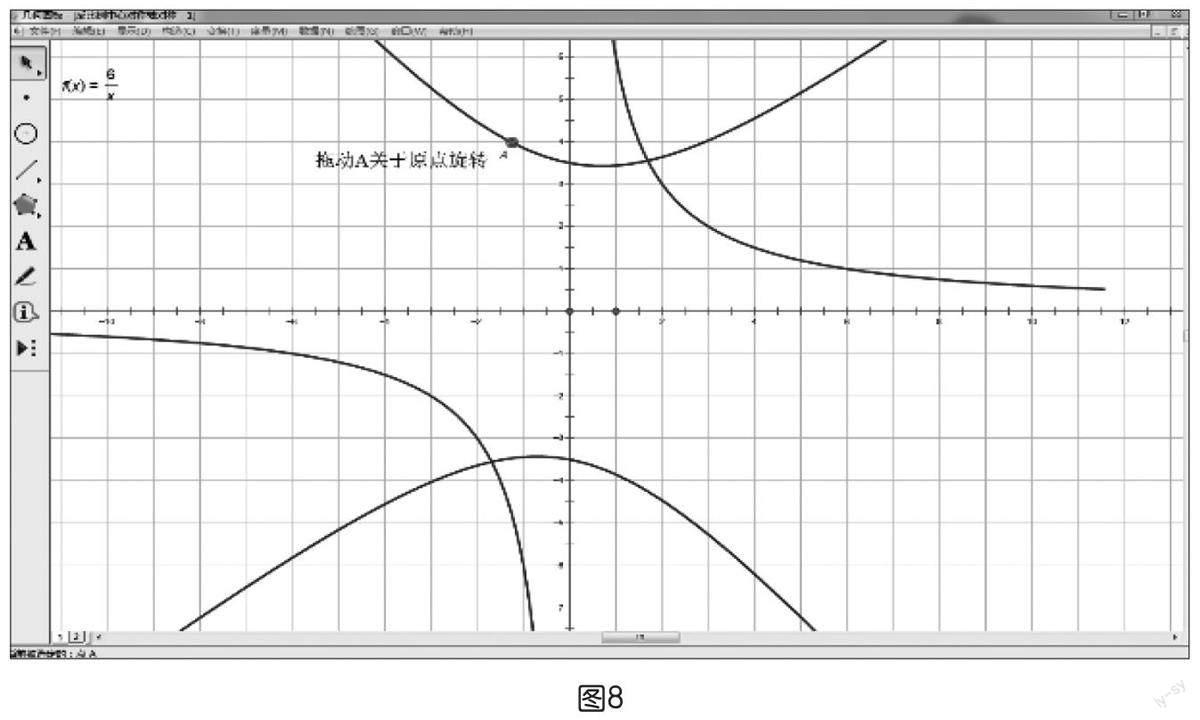
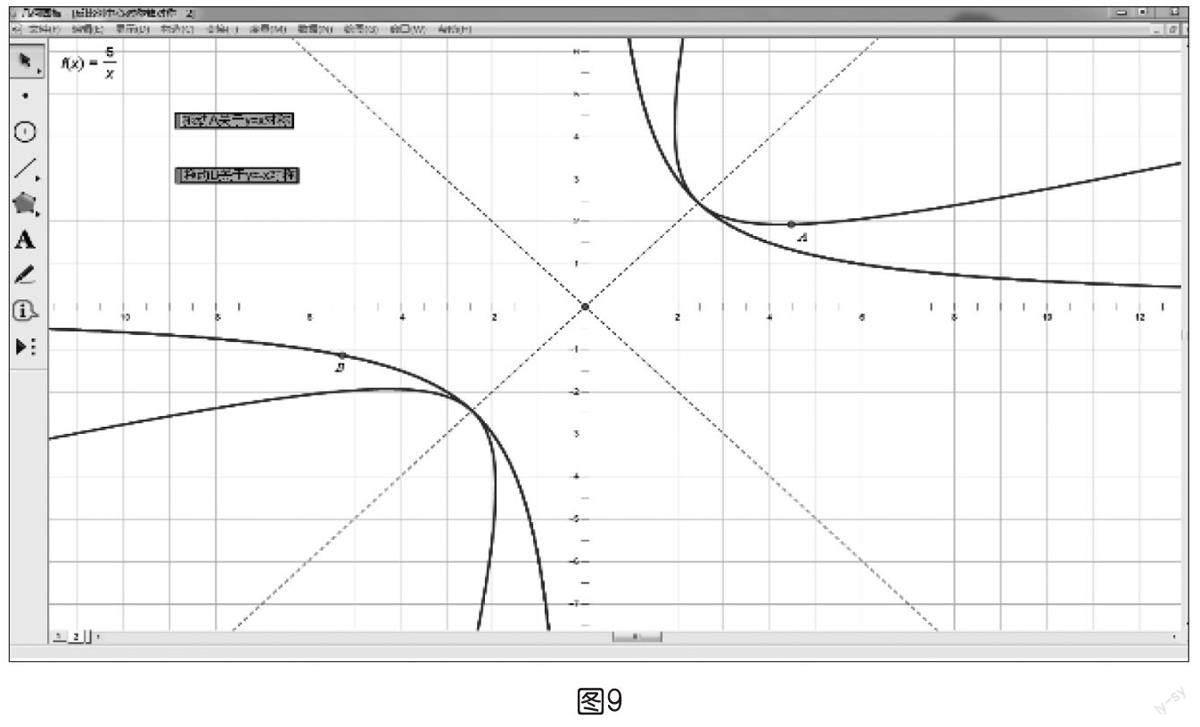
預(yù)期：若教具操作后效果不明顯，則出示如圖8、下頁圖9所示的幾何畫板進行動態(tài)演示。

（2）環(huán)節(jié)二：典例練習

課件：通過課件出示例題。

目的：通過練習，加強學生對反比例函數(shù)圖象與性質(zhì)的理解，形成相應(yīng)的技能。

預(yù)期：此環(huán)節(jié)是為了考查學生應(yīng)用所學知識解決問題的能力，并規(guī)范解題的步驟。

（3）環(huán)節(jié)三：課堂小結(jié)

課件：通過課件出示課堂小結(jié)板書。

目的：回顧探索畫函數(shù)圖象的過程，進一步感悟由函數(shù)圖象得出的性質(zhì)。

預(yù)期：引導(dǎo)學生回憶本節(jié)課的收獲——畫函數(shù)圖象的步驟、如何避免畫圖過程中典型的錯誤、反比例函數(shù)圖象的形狀、k與位置的關(guān)系，以及對稱性。

（4）環(huán)節(jié)四：達標測試（略）

（5）環(huán)節(jié)五：課后作業(yè)（略）

關(guān)鍵技術(shù)處理

1.幾何畫板利用參數(shù)變化取點

①建立適當大小的坐標系；②點型改為最小（大量取點，點太大重疊不美觀）；③新建參數(shù)（表示接下來從-5開始取點）；④參數(shù)屬性，改變以0.1單位，精確度改為十分之一（取決于前面

⑤利用點C、點B與坐標軸構(gòu)建矩形；⑥構(gòu)造四邊形內(nèi)部顏色（這樣圖形變化時會比較醒目）；⑦追蹤點C，然后在x軸上慢慢拖動點B；⑧點C的移動軌跡慢慢畫了出來。

4.以微視頻的形式呈現(xiàn)幾何畫板作圖

筆者利用Camtasia錄制幾何畫板的操作，并加上字幕輔助觀看；利用Pr剪輯視頻，在講解作圖原理部分常速播放，在操作部分加速播放。若用幾何畫板現(xiàn)場操作，即使再熟練，也需要一定量的時間。而用視頻的形式優(yōu)化了現(xiàn)場的操作，這樣能在較短時間內(nèi)給學生提供更多的函數(shù)描點的圖象，并多角度去分析圖象的特點。

幕前幕后

通過制作本次課件筆者體會到：①選題是創(chuàng)作多媒體課件最關(guān)鍵的一步，并不是每節(jié)課都適用于多媒體課件制作。應(yīng)認真研究教材與學生的特點，從大概念、大單元的角度去分析每一節(jié)課的重難點是什么、常規(guī)手段是否能夠解決、用什么信息技術(shù)手段可以突破。②運用多媒體軟件參與教學要適度，現(xiàn)代技術(shù)手段的實施一定是服務(wù)于學生的，而不是為了展示高科技，所以要掌握幾何畫板中的各種作圖技巧與相關(guān)數(shù)學原理的聯(lián)系。③在多媒體課件制作完成后，要通過上課驗證：信息技術(shù)是為了突破難點還是只是一個花邊效果？換成其他手段是否也能解決這個問題？學生的學習效果如何？通過收集反饋的信息，進行優(yōu)化修正，從而達到信息技術(shù)真正為課堂服務(wù)的目的。