表面粗糙度對(duì)橡塑O形圈往復(fù)密封性能的影響

梁鶴，王騰飛，王文中，郭玉龍

(1.北京理工大學(xué)機(jī)械與車(chē)輛學(xué)院，北京 100081；2.中國(guó)機(jī)械設(shè)備工程股份有限公司，北京 100073 )

橡塑密封件是液壓系統(tǒng)的重要零部件，密封件失效輕則引起液體泄漏造成一定的資源浪費(fèi)和環(huán)境污染，重則機(jī)器失效，甚至引發(fā)安全事故。密封的重要性已經(jīng)引起許多發(fā)達(dá)國(guó)家的高度重視，潤(rùn)滑設(shè)計(jì)是密封設(shè)計(jì)的關(guān)鍵基礎(chǔ)，良好的潤(rùn)滑性能對(duì)于提高液壓系統(tǒng)的使用壽命具有重要的作用。

20世紀(jì)中葉以來(lái)，國(guó)內(nèi)外學(xué)者對(duì)橡塑往復(fù)密封進(jìn)行了深入的研究。SALANT等[1]假設(shè)活塞桿表面在跑合后為光滑表面，建立了平均流量模型，開(kāi)展了粗糙度對(duì)密封性能影響的研究，發(fā)現(xiàn)粗糙度是決定密封是否泄漏的主要因素。NIKAS和SAYLES[2-4]分別針對(duì)矩形圈和U形圈建立了數(shù)值仿真模型，研究發(fā)現(xiàn)在粗糙表面接觸情況下由于液體膜受到粗糙表面的擾動(dòng)而存在較小的壓力波動(dòng)，串聯(lián)密封結(jié)構(gòu)在高溫條件下泄漏量非常小或?yàn)?。CRUDU等[5]結(jié)合數(shù)值仿真和實(shí)驗(yàn)，分析了粗糙度的幾何分布和波長(zhǎng)對(duì)密封性能的影響，研究發(fā)現(xiàn)粗糙度對(duì)密封潤(rùn)滑性能有顯著影響。SCARAGGI等[6]結(jié)合多尺度平均場(chǎng)模型進(jìn)一步完善了軟彈流平均流量模型，研究了各向異性粗糙表面對(duì)密封性能的影響，并與實(shí)驗(yàn)?zāi)Σ烈驍?shù)對(duì)比驗(yàn)證了模型預(yù)測(cè)結(jié)果的合理性。歐陽(yáng)小平等[7]建立多場(chǎng)耦合平均流量模型，研究了航空高壓往復(fù)密封，發(fā)現(xiàn)了高溫、高壓、高速都會(huì)加劇密封的泄漏和磨損。王冰清[8]結(jié)合仿真和實(shí)驗(yàn)，研究了非牛頓流體、熱效應(yīng)、液膜水污染等對(duì)密封性能的影響。XIANG等[9]開(kāi)發(fā)了效率更高的基于平均流量模型的流-固耦合算法，提高了計(jì)算效率。

上述數(shù)值仿真研究多采用平均流量模型，無(wú)法詳細(xì)考察粗糙表面真實(shí)形貌的具體細(xì)節(jié)對(duì)密封性能的影響。閆曉亮等[10]建立了一維確定性混合潤(rùn)滑模型，考慮粗糙表面的具體細(xì)節(jié)，分析了正弦粗糙表面的粗糙度幅值和波長(zhǎng)對(duì)密封性能的影響，研究發(fā)現(xiàn)粗糙度幅值增大有利于減小泄漏量，粗糙度幅值和波長(zhǎng)增大使摩擦因數(shù)減小。目前尚缺乏對(duì)三維非高斯粗糙表面真實(shí)形貌的研究，因此本文作者針對(duì)橡塑O形圈往復(fù)密封建立了三維確定性混合潤(rùn)滑模型，開(kāi)展了非高斯表面粗糙度、自相關(guān)長(zhǎng)度比值和紋理方向?qū)γ芊庑阅苡绊懙难芯浚芯拷Y(jié)果對(duì)密封的設(shè)計(jì)和使用提供理論指導(dǎo)。

1 混合潤(rùn)滑模型

橡塑O形圈屬于典型的非線(xiàn)性材料，其在外界壓力作用下產(chǎn)生毫米級(jí)的宏觀變形。相較于該變形量，潤(rùn)滑接觸產(chǎn)生的微米級(jí)微觀膜厚量級(jí)小很多，直接利用數(shù)值編程耦合求解該變形難度較大。因此在保證較高計(jì)算精度的前提下，文中模型結(jié)合有限元分析和混合潤(rùn)滑模型進(jìn)行求解：首先利用有限元分析求解獲得密封圈的宏觀變形；然后建立確定性混合潤(rùn)滑模型，以有限元計(jì)算得到的壓力分布和接觸寬度為初始條件，進(jìn)一步求解潤(rùn)滑接觸區(qū)的壓力和膜厚分布，從而計(jì)算密封性能的相關(guān)參數(shù)。

1.1 有限元模型

圖1所示為O形圈密封結(jié)構(gòu)，由溝槽、O形圈和柱塞桿組成。柱塞桿直徑D=32 mm，O形圈截面直徑Dseal=3.3 mm，選用丁腈橡膠材料，彈性模量E=25 MPa，泊松比υ=0.499，依據(jù)工程實(shí)際選擇O形圈初始?jí)嚎s率為15%。

圖1 O形圈受壓變形示意Fig.1 Schematic of compression deformation of O-ring

文中計(jì)算所用丁腈橡膠材料采用經(jīng)典的Mooney-Rivlin模型表征：

W=C10(I1-3)+C01(I2-3)+(J-1)2/d

(1)

式中：W為應(yīng)變能密度；I1、I2分別為應(yīng)變張量的第一和第二不變量；d為材料體積變化率；C10、C01和J為M-R參數(shù)，根據(jù)參考文獻(xiàn)[8]，設(shè)置其值分別為1.87 MPa、0.47 MPa和0.000 11。

首先采用有限元軟件計(jì)算密封靜接觸壓力。由其結(jié)構(gòu)特性可知，O形圈密封可以簡(jiǎn)化為二維軸對(duì)稱(chēng)模型。有限元網(wǎng)格劃分模型如圖2所示，對(duì)柱塞桿和溝槽采用映射化結(jié)構(gòu)網(wǎng)格，而對(duì)O形圈采用四邊形自由網(wǎng)格以保證計(jì)算收斂性，對(duì)O形圈與柱塞桿接觸部分進(jìn)行局部加密以提高計(jì)算結(jié)果的精度。設(shè)密封液體壓力為5 MPa，施加液體壓力前后靜接觸壓力分布psc如圖3所示，施加液體壓力后O形圈側(cè)面也發(fā)生擠壓，與柱塞桿的接觸壓力增大。

圖2 O形圈密封有限元網(wǎng)格模型Fig.2 Finite element mesh model of O-ring seal

圖3 施加密封壓力前后接觸壓力分布(MPa)Fig.3 Contact pressure distribution before and after application of sealing pressure(MPa)：(a)before application of pressure；(b) applied pressure of 5 MPa

將有限元計(jì)算所得O形圈的接觸壓力和接觸寬度作為潤(rùn)滑數(shù)值分析的初始值。因?yàn)橛湍ず穸葘?duì)O形圈的變形影響很小，文中忽略其對(duì)密封圈受壓載荷的影響，以有限元計(jì)算中O形圈的干接觸載荷作為潤(rùn)滑計(jì)算的載荷。

1.2 界面流體模型

由于柱塞桿的粗糙度值僅為O形圈粗糙度值的1/10[1]，因此文中忽略柱塞桿表面粗糙度，選用確定性模型對(duì)O形圈表面粗糙度展開(kāi)細(xì)致的研究。假設(shè)流體為層流，不考慮空化效應(yīng)，采用統(tǒng)一Reynolds方程系統(tǒng)法求解粗糙峰接觸區(qū)域接觸壓力和非接觸區(qū)域油膜壓力。接觸區(qū)域和非接觸區(qū)域通過(guò)臨界膜厚hlimit劃分，油膜厚度小于臨界膜厚時(shí)為接觸區(qū)域。溫詩(shī)鑄[11]提出邊界潤(rùn)滑膜厚范圍為0.005～0.01 μm，因此選取hlimit為0.005 μm。設(shè)p為潤(rùn)滑區(qū)域壓力分布，當(dāng)液膜厚度大于臨界膜厚時(shí)，壓力為液膜壓力pl，即p=pl，pl滿(mǎn)足雷諾方程：

(2)

式中：η為潤(rùn)滑油黏度 (Pa·s)；pl為液膜壓力(Pa)；u為平均速度，u=U/2，U為活塞桿運(yùn)動(dòng)速度(m/s)；x、y為坐標(biāo)變量(m)。

當(dāng)液膜厚度小于臨界膜厚時(shí)，壓力為接觸壓力pc，即p=pc，pc用式(3)求解。

(3)

O形圈密封為線(xiàn)接觸，由于其在軸向方向即x方向的接觸寬度遠(yuǎn)小于在周向方向即y方向的接觸長(zhǎng)度(如圖1所示)，為了提高計(jì)算效率和精度并同時(shí)考慮三維粗糙表面接觸情況，文中選用REN等[12]提出的三維線(xiàn)接觸潤(rùn)滑模型。假設(shè)粗糙度以及壓力和膜厚分布在y方向上周期性重復(fù)，從而沿y向截取較小一段為研究對(duì)象，模型不考慮柱塞桿曲率的影響，簡(jiǎn)化為三維平面線(xiàn)接觸。在x方向采用離散卷積和快速傅里葉變換算法(CD-FFT)，在y方向采用帶重復(fù)填充的離散卷積和快速傅里葉變換算法(DCD-FFT)。在y方向上的邊界采用周期性邊界條件，如式(4)所示。

(4)

1.3 粗糙表面生成模型

基于ZHANG等[13]的模型生成非高斯粗糙表面，通過(guò)高度標(biāo)準(zhǔn)差σ、自相關(guān)長(zhǎng)度β、峰度K和偏態(tài)S4個(gè)參數(shù)來(lái)描述表面特性。采用指數(shù)形式的自相關(guān)函數(shù)，函數(shù)表達(dá)式如式(5)所示。

(5)

式中：βx和βy分別為x方向和y方向的自相關(guān)長(zhǎng)度，βx=βy表示各向同性的粗糙表面。

令γ=βx/βy，γ>1時(shí)生成的粗糙表面為橫向紋理粗糙表面，γ值越大，粗糙峰長(zhǎng)寬比越小，沿x方向輪廓不平度間距的平均值相對(duì)越大。圖4所示為不同γ值的粗糙表面，γ=1時(shí)為各向同性粗糙表面，γ=10時(shí)為橫向紋理粗糙表面。

圖4 不同γ值的粗糙表面Fig.4 Rough surfaces with different γ values：(a)γ=1； (b)γ=10

文中選取βx=10，βy=400，生成紋理方向與y軸平行的粗糙表面，再通過(guò)對(duì)粗糙表面進(jìn)行旋轉(zhuǎn)，生成不同紋理方向的粗糙表面；柱塞桿運(yùn)動(dòng)方向?yàn)閤方向，設(shè)紋理方向與y軸夾角為θ，θ= 0時(shí)為橫向紋理。θ分別為0、π/2的粗糙表面如圖5所示。

1.4 膜厚方程

潤(rùn)滑液膜厚度根據(jù)如下方程計(jì)算：

h(x，y)=h0+s(x，y)+v(x，y)+σ(x，y)

(6)

式中：h0為O形圈和柱塞桿的接近距離；s(x，y)為表面幾何尺寸變化引起的液膜厚度變化；v(x，y)為液膜的產(chǎn)生引起的O形圈微觀變形；σ(x，y)為O形圈表面粗糙度。

在潤(rùn)滑計(jì)算中，v(x，y)是由于液膜的產(chǎn)生而引起的微小變形，可認(rèn)為其符合小變形理論[14]。因而文中采用下式計(jì)算O形圈微觀變形[15]：

(7)

1.5 耦合模型的計(jì)算流程

文中先根據(jù)密封的幾何、材料等參數(shù)建立二維軸對(duì)稱(chēng)有限元模型，計(jì)算得到接觸壓力分布和接觸寬度，然后代入確定性潤(rùn)滑模型求解得到壓力分布和膜厚分布，計(jì)算平均膜厚、摩擦力、泄漏率和接觸面積比。模型的計(jì)算流程如圖6所示。

圖6 數(shù)值求解流程Fig.6 The flow of numerical solution

2 結(jié)果與分析

文中選取如下參數(shù)：柱塞桿直徑D=32 mm，O形圈截面直徑Dseal=3.3 mm，O形圈彈性模量E=25 MPa，O形圈徑向壓縮量δ=0.496 mm，泊松比υ=0.499，Mooney-Rivlin參數(shù)C10=1.87 MPa，C01=0.47 MPa，J=0.000 11，介質(zhì)動(dòng)力黏度η=0.038 7 Pa·s，介質(zhì)黏壓系數(shù)α=2.0×10-8，密封壓力回程pseal=0.1 MPa，進(jìn)程pseal=5 MPa，干摩擦因數(shù)fc=0.2。

2.1 計(jì)算結(jié)果及驗(yàn)證

2.1.1 計(jì)算結(jié)果

模型在潤(rùn)滑計(jì)算過(guò)程中考慮了粗糙表面真實(shí)形貌對(duì)壓力和膜厚分布的直接影響，可以對(duì)壓力和膜厚分布的具體情況進(jìn)行分析。圖7所示為回程階段壓力和膜厚的三維分布，可知：與γ=1時(shí)相比γ=10時(shí)壓力和膜厚分布出現(xiàn)明顯的橫向紋理。圖8所示為γ=10時(shí)，不同粗糙度條件下y=0.14 mm處的壓力和膜厚截面分布，可知：Ra越大，壓力和膜厚的波動(dòng)越大。

圖7 壓力和膜厚三維分布 (U=0.3 m/s，Ra=0.4 μm)Fig.7 Three-dimensional distribution of pressure and film thickness (U=0.3 m/s，Ra=0.4 μm)：(a)pressure distribution when γ=1；(b)film thickness when γ=1；(c)pressure distribution when γ=10；(d)film thickness when γ=10

圖8 壓力和膜厚截面分布(U=0.3 m/s)Fig.8 Cross sectional distribution of pressure and film thickness(U=0.3 m/s)

2.1.2 計(jì)算結(jié)果驗(yàn)證

將文中模型密封液體壓力設(shè)置為6 MPa，采用文獻(xiàn)[16]的試驗(yàn)參數(shù)進(jìn)行計(jì)算，結(jié)果如圖9所示。可見(jiàn)，模型結(jié)果和文獻(xiàn)試驗(yàn)結(jié)果吻合較好，驗(yàn)證了文中模型的正確性。

圖9 模型計(jì)算結(jié)果驗(yàn)證Fig.9 Verification of model calculation results

進(jìn)一步，根據(jù)HOOKE和O′DONOGHUE[17]提出的軟彈流潤(rùn)滑接觸驗(yàn)證方法，對(duì)入口區(qū)和出口區(qū)壓力分布進(jìn)行驗(yàn)證，驗(yàn)證結(jié)果如圖10所示。可見(jiàn)文中數(shù)值仿真結(jié)果與文獻(xiàn)所給經(jīng)驗(yàn)公式計(jì)算結(jié)果基本吻合，證明了仿真計(jì)算結(jié)果的正確性。但因?yàn)榻?jīng)驗(yàn)公式基于赫茲接觸理論因而存在一定差異。

圖10 入口區(qū)和出口區(qū)壓力驗(yàn)證

2.2 表面粗糙度對(duì)密封性能的影響

柱塞桿運(yùn)動(dòng)速度分別取U=0.05 m/s和U=0.3 m/s，取自相關(guān)長(zhǎng)度比值γ=4，將Ra取不同值的粗糙表面代入潤(rùn)滑模型進(jìn)行計(jì)算，結(jié)果如圖11所示。其中平均膜厚是密封接觸區(qū)中心2/3區(qū)域(如圖8所示)的液膜厚度平均值，泄漏率為正值表示密封處于液體泄漏狀態(tài)，為負(fù)值表示密封處于液體泵回狀態(tài)。圖11 (a)給出了摩擦因數(shù)隨Ra值的變化，摩擦因數(shù)隨Ra值增加而增大，相同速度下回程摩擦因數(shù)小于進(jìn)程摩擦因數(shù)。圖11 (b) 反映了平均膜厚隨Ra值的變化，U=0.05 m/s時(shí)平均膜厚隨Ra增加先增大后減小，U=0.3 m/s時(shí)平均膜厚隨Ra增加而增大，相同速度下回程平均膜厚大于進(jìn)程平均膜厚。圖11 (c)反映了泄漏率隨Ra值的變化，U=0.05 m/s時(shí)回程和進(jìn)程泄漏率均為正值，密封始終處于泄漏狀態(tài)，回程泄漏率隨Ra值增加先增大后減小，進(jìn)程泄漏率隨Ra值增加先減小后增大；U=0.3 m/s時(shí)進(jìn)程泄漏率為負(fù)值，發(fā)生液體泵回，回程和進(jìn)程泄漏率的絕對(duì)值均隨Ra值增加而增大。圖11(d)反映了接觸面積比隨Ra值的變化，接觸面積比隨Ra值增加而增大，相同速度下回程接觸面積比小于進(jìn)程接觸面積比。

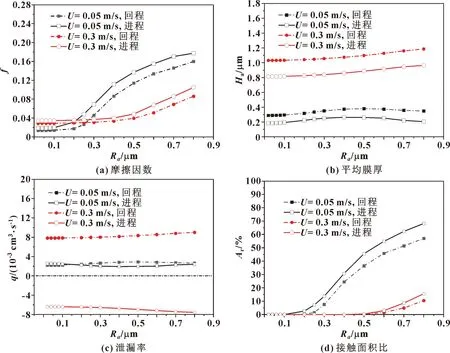
圖11 表面粗糙度值Ra對(duì)密封性能的影響Fig.11 Influence of surface roughness amplitude Ra on sealing performances：(a)friction coefficient； (b)average film thickness；(c)leakage；(d)contact area ratio

分析可知，粗糙度主要通過(guò)改變接觸面積比影響密封的摩擦因數(shù)，隨著Ra值的增加越來(lái)越多的粗糙峰發(fā)生接觸導(dǎo)致摩擦因數(shù)增大。接觸面積比小于40%時(shí)，Ra值增加引起流體動(dòng)壓效應(yīng)增強(qiáng)，使得平均膜厚和泄漏率增大。接觸面積比達(dá)到40%時(shí)，平均膜厚和泄漏率達(dá)到最大值，Ra值增加引起流體動(dòng)壓效應(yīng)減弱，平均膜厚和泄漏率開(kāi)始減小。U=0.05 m/s時(shí)進(jìn)程階段壓差引起的泊肅葉流和速度引起的庫(kù)埃特流方向相反，但泊肅葉流占據(jù)主導(dǎo)地位，使密封處于泄漏狀態(tài)，流體動(dòng)壓效應(yīng)增強(qiáng)時(shí)庫(kù)埃特流增強(qiáng)，對(duì)泊肅葉流的抵消作用增強(qiáng)，使泄漏率降低。

2.3 自相關(guān)長(zhǎng)度比值對(duì)密封性能的影響

由1.3節(jié)分析可知，γ>1時(shí)粗糙表面為橫向紋理，γ值越大，粗糙峰長(zhǎng)寬比越小，沿x方向輪廓不平度間距的平均值越大。柱塞桿運(yùn)動(dòng)速度取U=0.05 m/s，粗糙度取Ra=0.4 μm，計(jì)算不同γ值的粗糙表面對(duì)密封性能的影響，結(jié)果如圖12所示。在回程階段，隨著γ值的增加，摩擦因數(shù)和接觸面積比先迅速減小后緩慢增大，平均膜厚和泄漏率逐漸減小，泄漏率為正值，密封處于泄漏狀態(tài)。接觸面積比大于5%，明顯存在粗糙峰接觸，密封處于混合潤(rùn)滑狀態(tài)。在進(jìn)程階段，隨著γ值的增加，摩擦因數(shù)和接觸面積比先迅速減小后趨于平穩(wěn)，平均膜厚和泄漏率先減小后增大，泄漏率為正值，表明密封處于液體泄漏狀態(tài)，原因是壓差引起的泊肅葉流占據(jù)主導(dǎo)地位，速度引起的庫(kù)埃特流相對(duì)較弱，未發(fā)生液體泵回。接觸面積比大于15%，始終存在大量粗糙峰接觸，處于混合潤(rùn)滑狀態(tài)。

圖12 U=0.05 m/s時(shí)γ值對(duì)密封性能的影響Fig.12 Influence of different γ values on sealing performances at U=0.05 m/s：(a)friction coefficient； (b)average film thickness；(c)leakage；(d)contact area ratio

柱塞桿速度增加到U=0.3 m/s，計(jì)算不同γ值的粗糙表面對(duì)密封性能的影響如圖13所示。回程階段，不同γ值的粗糙表面對(duì)密封性能的影響規(guī)律與U=0.05 m/s時(shí)的影響規(guī)律基本相同，但影響幅度相對(duì)較小。由于接觸面積比較小，γ值由1增大到4時(shí)，接觸面積比降低了0.04%，平均膜厚上升了0.5%，摩擦因數(shù)降低了6%，泄漏率上升了0.3%。比較發(fā)現(xiàn)平均膜厚的變化大于接觸面積比的變化，不同γ值的粗糙表面主要通過(guò)增大平均膜厚從而改善密封的摩擦因數(shù)。進(jìn)程階段，不同γ值的粗糙表面對(duì)摩擦因數(shù)的影響規(guī)律與回程階段的影響規(guī)律相一致。此時(shí)泄漏率為負(fù)值，發(fā)生液體泵回，原因是此時(shí)速度較大，速度引起的庫(kù)埃特流占主導(dǎo)地位。

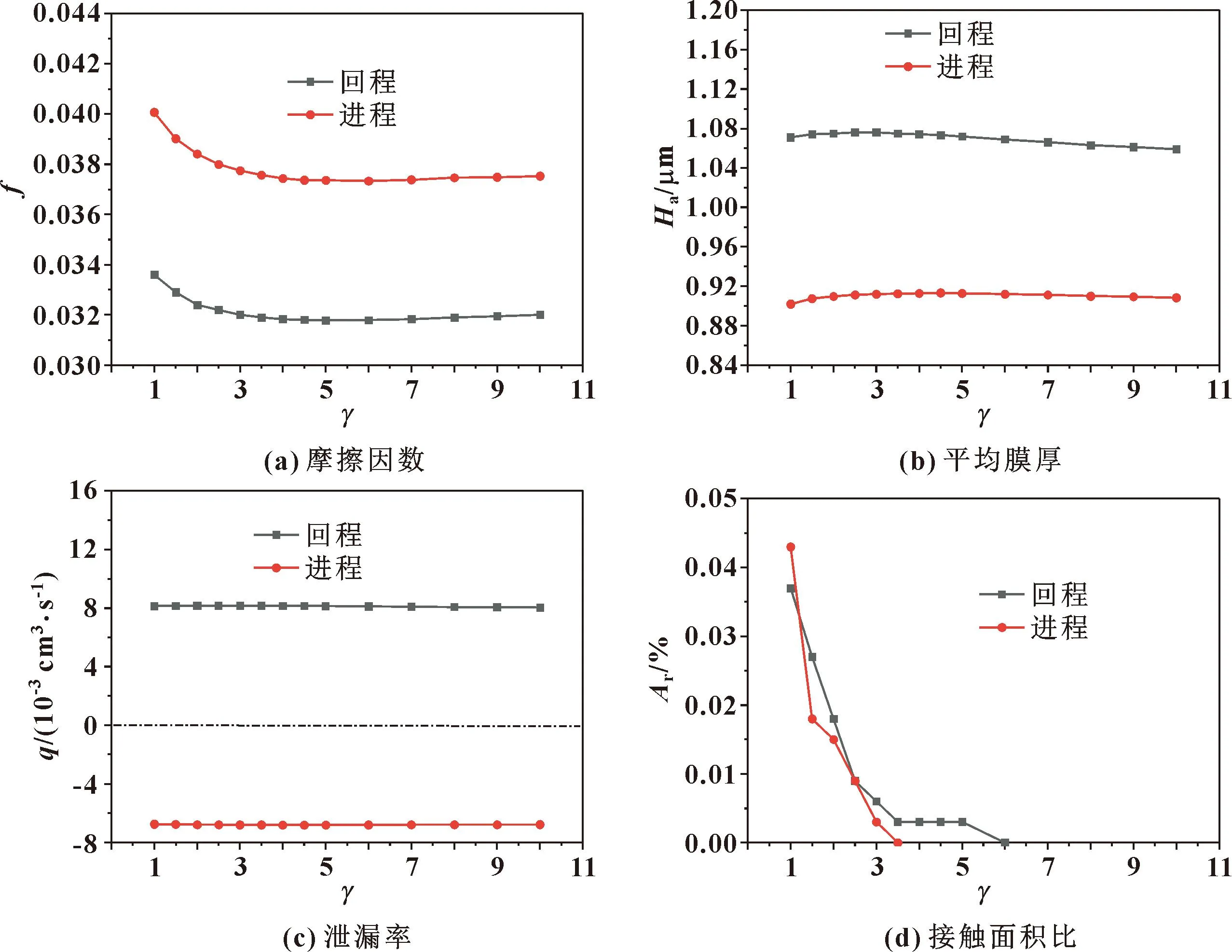
圖13 U=0.3 m/s時(shí)γ值對(duì)密封性能的影響Fig.13 Influence of different γ values on sealing performances at U=0.3 m/s：(a)friction coefficient； (b)average film thickness；(c)leakage；(d)contact area ratio

綜上分析可知，潤(rùn)滑狀態(tài)為混合潤(rùn)滑時(shí)，γ值對(duì)摩擦因數(shù)和泄漏率影響顯著。γ值主要通過(guò)影響接觸面積比改變密封的摩擦因數(shù)，同時(shí)通過(guò)影響平均膜厚改變泄漏率。

2.4 紋理方向?qū)γ芊庑阅艿挠绊?/h3>

取粗糙度值為0.4 μm，生成具有特定紋理方向的粗糙表面，其對(duì)密封性能的影響如圖14所示。圖14(a)和(e)所示為回程和進(jìn)程時(shí)不同紋理方向粗糙表面的摩擦因數(shù)，比較θ=0、π/10、π/4和π/2等4個(gè)紋理方向粗糙表面的摩擦因數(shù)可以發(fā)現(xiàn)，無(wú)論是進(jìn)程還是回程階段，橫向紋理粗糙表面(θ=0)的摩擦因數(shù)都要小于縱向紋理(θ=π/2)，這與ANGERHAUSEN等[18]的實(shí)驗(yàn)結(jié)果相一致；θ=π/10的斜紋理粗糙表面可獲得最小的摩擦因數(shù)；隨著速度增加，紋理方向?qū)δΣ烈驍?shù)的影響減小。圖14(b)和(f)所示為回程和進(jìn)程時(shí)不同紋理方向粗糙表面的平均膜厚，可見(jiàn)平均膜厚的變化規(guī)律與摩擦因數(shù)的變化規(guī)律基本相反，速度大于等于0.3 m/s時(shí)，橫向紋理粗糙表面的平均膜厚大于縱向紋理粗糙表面；θ=π/10的粗糙表面的平均膜厚最大；速度增大，紋理方向?qū)ζ骄ず竦挠绊憸p小。圖14(c)和(g)所示為回程和進(jìn)程時(shí)不同紋理方向粗糙表面的泄漏率，可見(jiàn)進(jìn)程階段速度大于等于0.3 m/s時(shí)泄漏率為負(fù)值，發(fā)生液體泵回；泄漏率的相對(duì)變化趨勢(shì)和平均膜厚的相對(duì)變化趨勢(shì)一致。圖14(d)和(h)所示為回程和進(jìn)程時(shí)不同紋理方向粗糙表面的接觸面積比，可見(jiàn)橫向紋理粗糙表面的接觸面積比小于縱向紋理粗糙表面；θ=π/10的粗糙表面的接觸面積比最小；速度大于0.3 m/s時(shí)，不同紋理方向粗糙表面的接觸面積比逐漸降為0，這與圖14(a)和(e)中相應(yīng)摩擦因數(shù)的變化規(guī)律相一致；回程的摩擦因數(shù)和接觸面積比相對(duì)進(jìn)程較小，平均膜厚相對(duì)進(jìn)程較大。綜上，不同紋理方向粗糙表面通過(guò)改變接觸面積比和平均膜厚來(lái)影響摩擦因數(shù)，通過(guò)改變平均膜厚來(lái)影響泄漏率。

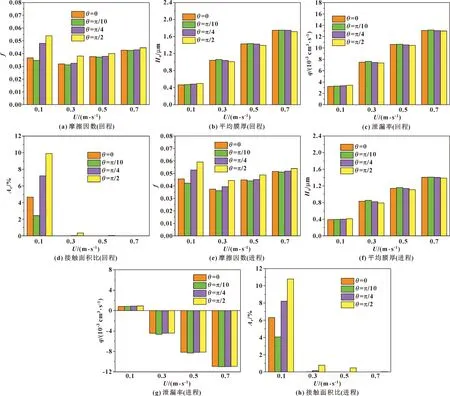
圖14 紋理方向?qū)γ芊庑阅艿挠绊慒ig.14 Influence of different texture directions on sealing performances：(a)friction coefficient at outstroke；(b)average film thickness at outstroke；(c)leakage at outstroke；(d)contact area ratio at outstroke；(e)friction coefficient at instroke；(f)average film thickness at instroke；(g)leakage at instroke；(h)contact area ratio at instroke

基于以上分析給出紋理方向?qū)γ芊饽Σ烈驍?shù)影響的解釋?zhuān)核俣葹?.1 m/s時(shí)，密封處于混合潤(rùn)滑狀態(tài)，橫向紋理粗糙表面和θ=π/10的粗糙表面的接觸面積比相對(duì)縱向紋理粗糙表面小，粗糙峰接觸相對(duì)較少，使其對(duì)液體的阻礙作用相對(duì)較弱，因而不具有平均膜厚上的相對(duì)優(yōu)勢(shì)，但較小的接觸面積使其具有較小的摩擦因數(shù)；速度為0.3 m/s時(shí)，密封處于由混合潤(rùn)滑向流體動(dòng)壓潤(rùn)滑的過(guò)渡區(qū)，粗糙峰處膜厚較小或發(fā)生接觸，橫向紋理粗糙表面連續(xù)的粗糙峰增強(qiáng)了其對(duì)液體的積聚作用，使平均膜厚增大，摩擦因數(shù)減小；速度為0.7 m/s時(shí)，密封處于流體動(dòng)壓潤(rùn)滑，粗糙峰處液膜厚度較大，連續(xù)的粗糙峰對(duì)液體的阻礙作用減小，不同紋理方向粗糙表面摩擦因數(shù)的差異減小。所以紋理方向通過(guò)改變粗糙表面的接觸特性和對(duì)液體的積聚特性2個(gè)因素來(lái)影響密封的摩擦因數(shù)，且速度不同，潤(rùn)滑狀態(tài)不同，2個(gè)因素的主次地位不同，速度較低時(shí)，接觸特性的作用處于主要地位，速度較大時(shí)，對(duì)液體的積聚特性的作用處于主要地位。

3 結(jié)論

針對(duì)橡塑O形圈往復(fù)密封，建立了三維確定性混合潤(rùn)滑模型，開(kāi)展了非高斯表面粗糙度、自相關(guān)長(zhǎng)度比值和紋理方向?qū)γ芊庑阅苡绊懙难芯俊Ｖ饕Y(jié)論如下：

(1)隨著粗糙度Ra的增大，潤(rùn)滑狀態(tài)由流體動(dòng)壓潤(rùn)滑轉(zhuǎn)變?yōu)榛旌蠞?rùn)滑時(shí)，摩擦因數(shù)明顯增大；低速時(shí)平均膜厚先增大后減小，低速回程時(shí)泄漏率先增大后減小，低速進(jìn)程時(shí)泄漏率先減小后增大，臨界接觸面積比約為40%。

(2)對(duì)于橫向紋理粗糙表面，當(dāng)潤(rùn)滑狀態(tài)為混合潤(rùn)滑時(shí)，回程階段摩擦因數(shù)隨γ值增加顯著降低后緩慢增加，進(jìn)程階段摩擦因數(shù)隨γ值增加顯著降低后趨于平穩(wěn)；回程階段泄漏率隨γ值增加而逐漸降低，進(jìn)程階段泄漏率隨γ值增加先降低后增加。可設(shè)計(jì)合適的γ值同時(shí)獲得較小的摩擦因數(shù)和泄漏率。

(3)對(duì)于不同紋理方向的粗糙表面，橫紋粗糙表面的摩擦因數(shù)小于縱紋粗糙表面，θ=π/10的粗糙表面可以獲得最小的摩擦因數(shù)。低速下θ=π/10的粗糙表面具有最好的接觸特性，接觸面積比最低，使摩擦因數(shù)最低；高速下θ=π/10的粗糙表面具有最好的液體積聚特性，平均膜厚最大，使摩擦因數(shù)最低。