函數展開計數在CLUTCH方法中的初步應用

黃金龍,曹良志,賀清明,秦 帥,吳宏春

(西安交通大學 核科學與技術學院,陜西 西安 710049)

核數據是核反應堆中子學計算的重要輸入參數,其敏感性分析結果可反映對響應參數敏感的核數據,進而對核反應堆堆芯設計和不確定度量化[1]等有重要的指導意義。反復裂變幾率(IFP)方法[2]被眾多蒙特卡羅程序用于k特征值對核數據的敏感性分析[3-6],該方法的主要缺點是,內存占用與每代模擬粒子數呈正比,當每代模擬粒子數較大時,內存占用甚至不可接受。Kiedrowski在MCNP中提出稀疏矩陣[7]存儲方式,以降低IFP方法的內存使用。數據表明,采用稀疏矩陣方法可降低10～100倍的內存,但內存占用量依舊較大。Perfetti[8]提出CLUTCH方法[9-10]可在不損失結果精度的前提下,顯著降低內存占用。CLUTCH方法需要劃分網格來統計權重函數,且網格的大小[8]推薦為1 cm3,對于大規模問題(如壓水堆全堆問題),需要劃分大量網格來統計權重函數,在網格數量較多的情況下,保證權重函數收斂所需的粒子數是不可接受的。因此,本文將使用函數展開計數(FET)方法[11]對權重函數進行統計,提高統計權重函數的精度和效率,從而實現對大規模問題的高效率、高精度的連續能量核數據敏感性分析。

本文在蒙特卡羅程序NECP-MCX[12]上實現基于網格和函數展開計數方法的CLUTCH方法(CLUTCH-Mesh和CLUTCH-FET),以進行k特征值對核數據敏感性分析。以IFP方法[13]的計算結果為參考解,在Godiva、Flattop和AP1000全堆問題上對CLUTCH-Mesh和CLUTCH-FET方法進行驗證,并比較兩種方法的計算精度和效率。

1 理論方法

基于一階微擾理論,k特征值對核數據的靈敏度系數S可表示為:

Sk,Σx(r,E)=

(1)

其中:Σx(r,E)為x反應道在位置r處能量為E的宏觀截面;F為裂變項算子;S為散射項算子;T為碰撞項算子;ψ為中子通量;ψ*為共軛通量;〈,〉表示在相空間中積分。

由式(1)可看出,靈敏度系數是反應率和共軛通量的乘積,反應率在蒙特卡羅計數中容易統計,共軛通量可用IFP和CLUTCH方法求解。

1.1 CLUTCH方法

基于Contributon理論[14],相空間中某點P0處的共軛通量表達式為:

(2)

其中:Qs(P0)為粒子進入P0時的權重;χ(r,E)為r處出射能量為E的裂變譜;ν(E′)為入射能量為E′的裂變中子數;Σf(r,E′)為位置r處能量為E′的裂變截面;Ω′和Ω分別為中子的入射方向和出射方向;ψ(r,Ω′,E′|P0)為從P0點產生的中子在(r,Ω′,E′)處產生的中子通量;G(P0→r)為轉移函數,表示從P0處轉移到r處的中子通量;I*(r)為r處的權重函數。

權重函數I*(r)可根據未歸一的裂變譜的靈敏度系數求解,表達式為:

(3)

其中:D為式(1)的分母項;式(3)的分母表示初始代r處產生的裂變中子數,分子表示初始代由r處產生的裂變中子,經過幾個蒙特卡羅代的模擬后,在漸近代產生的中子數,因此,I*(r)為初始代r處平均產生的1個裂變中子在漸近代所產生的中子數。由于I*(r)只與空間位置有關,因此,通常基于空間網格對I*(r)進行統計且可在非活躍代統計得到。空間網格需要足夠精細,以準確描述權重函數的空間分布,同時需要模擬足夠多的粒子,以保證權重函數收斂。Perfetti[8]推薦,網格大小約為1 cm3,每個包含燃料的網格有1 000個非活躍代中子歷史,可保證權重函數足夠精細和收斂。以AP1000全堆問題為例,為保證網格大小約為1 cm3,需采用320×320×400的網格,為保證每個包含燃料的網格有1 000個非活躍代中子歷史,若每代模擬的中子數為106,則需要模擬的非活躍代數為28 581代,計算代價很大。因此,本文將使用函數展開計數方法對權重函數進行統計。

1.2 函數展開計數方法

1) FET系數求解

蒙特卡羅統計目標量φ(ξ)可用任意正交完備的基函數展開[11],表示為:

(4)

其中:ξ為歸一化后的相空間位置;n為函數展開階數;an為n階函數展開系數;φn為n階展開函數;ρ(ξ)為ξ處的權重函數。

根據基函數的正交性,可求解an:

(5)

其中,Γ為正交區域。

基于碰撞估計器,可得到an的估計表達式:

(6)

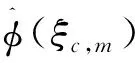
基于函數展開計數方法對式(3)進行統計時需分兩步:1) 初始代用函數展開計數方法統計裂變中子的分布,即統計分母,并保存函數展開系數;2) 由于初始代的裂變中子分布已得到,即式(3)的分母已知,再用函數展開計數方法對式(3)進行統計。

2) 勒讓德多項式

勒讓德多項式[15]是在區間[-1,1]上的正交多項式,n階勒讓德多項式可表示為:

(7)

其在區間[-1,1]上的正交性表示為:

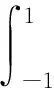
(8)

以基于勒讓德函數對三維空間變量φ(x,y,z)的函數展開為例進行說明。φ(x,y,z)可表示為:

(9)

其中:i,j,k分別為x,y,z方向展開系數索引;I,J,K分別為x,y,z方向展開階數;fi,j,k為函數展開系數,根據式(8)所示勒讓德函數的正交性,fi,j,k可根據式(10)求得。

(10)

基于碰撞估計器,可得到fi,j,k的估計式:

(11)

在非活躍代基于勒讓德多項式對權重函數進行函數展開計數,將得到的各階展開系數代入式(9),在活躍代即可得到空間各位置處的權重函數,將得到的權重函數代入式(2),用于共軛通量的求解,進而由式(1)計算得到靈敏度系數。

2 數值結果

基于上述理論方法在NECP-MCX中實現基于網格和函數展開計數的CLUTCH方法,用于k特征值對核數據的敏感性分析,并與IFP方法的計算結果比較,對比CLUTCH-Mesh和CLUTCH-FET方法的計算精度以及效率,其中計算效率用品質因子(FOM)衡量,品質因子的定義如式(12)所示。

(12)

其中:R為蒙特卡羅統計量的相對統計標準差;T為蒙特卡羅計算時間。品質因子越大,則計算效率越高。本文選取Godiva、Flattop和AP1000全堆問題進行驗證,使用ACE格式的ENDF/BⅦ.0數據庫。

2.1 Godiva問題

Godiva基準題[16]是一個均勻裸球裝置,材料為高濃鈾,半徑為8.741 cm,如圖1所示。靈敏度系數計算采用2 000個蒙特卡羅代,其中活躍代設為1 000代,每代模擬粒子數為105,塊的大小設置為10代。由于Godiva屬于一維問題,因此只需在半徑方向上對權重函數進行統計。

圖1 Godiva基準題Fig.1 Model for Godiva problem

選用不同展開階數的勒讓德多項式對權重函數進行統計,得到不同展開階數下CLUTCH-FET方法計算的靈敏度系數,如表1所列,其中Ave和RSD分別為靈敏度系數均值和相對統計漲落。

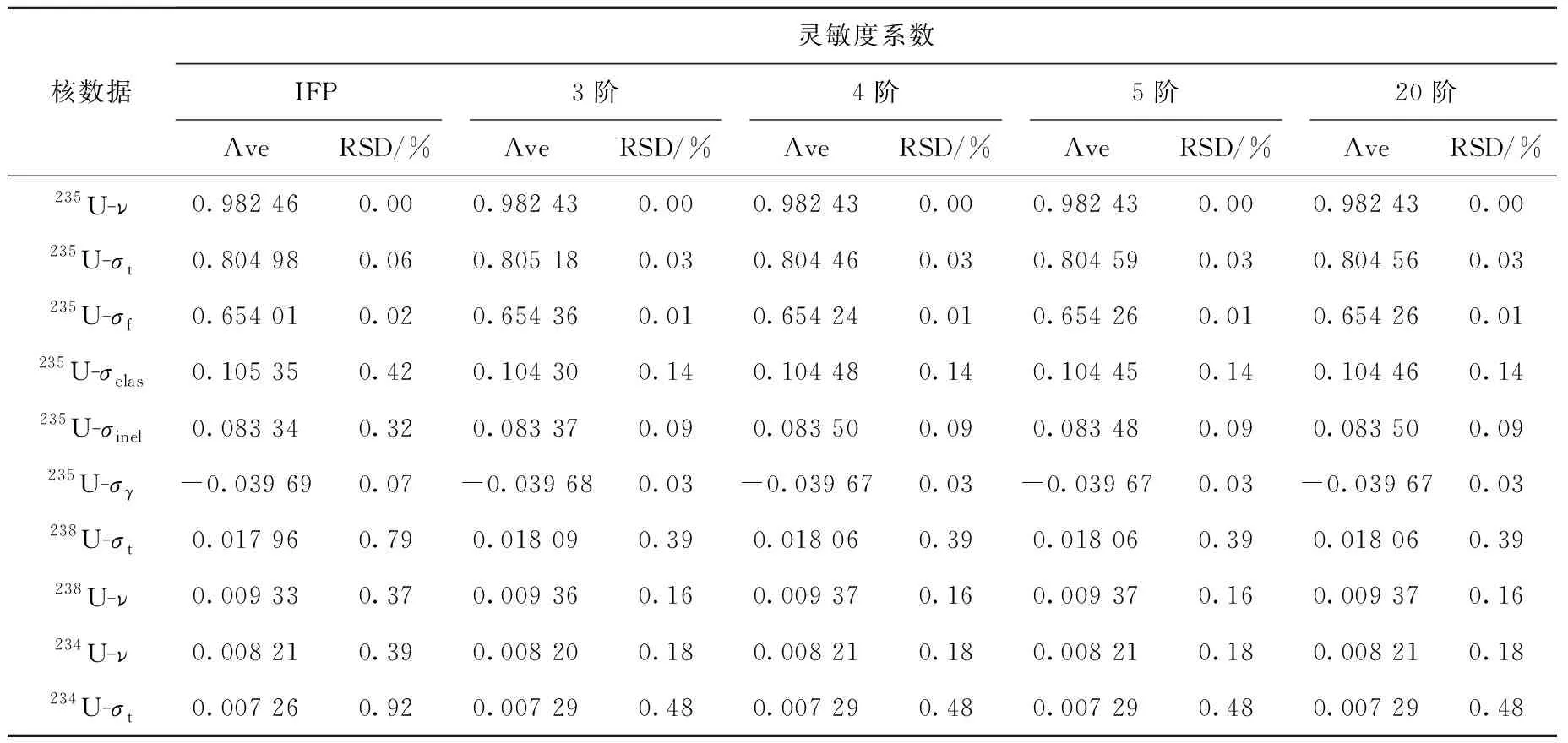
表1 Godiva問題中不同展開階數下CLUTCH-FET方法計算的靈敏度系數Table 1 Sensitivity coefficient of CLUTCH-FET method under different expansion orders for Godiva problem

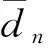
(13)

其中:m為反應道序號;M為反應道總數,即M=10;dn,m為勒讓德階數取n階時第m個反應道的靈敏度系數計算結果與參考解之間的差異,表示為:

(14)

其中:Aven,m和RSDn,m分別為展開系數階數取n的第m個反應道的靈敏度系數的均值和相對統計漲落;AveIFP,m和RSDIFP,m分別為IFP方法的第m個反應道的靈敏度系數的均值和相對統計漲落。

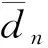
圖2 Godiva問題中不同展開階數下CLUTCH-FET方法計算的靈敏度系數與參考解間的差異Fig.2 Difference between sensitivity coefficients calculated by CLUTCH-FET under different expansion orders and reference for Godiva problem

CLUTCH-Mesh方法在半徑方向上劃分16等分作為統計權重函數的網格。CLUTCH-FET方法采用4階勒讓德多項式對權重函數在半徑方向上的分布進行統計,兩種方法求得的權重函數分布如圖3所示,IFP、CLUTCH-Mesh和CLUTCH-FET方法計算得到的靈敏度系數列于表2,FOM值示于圖4。

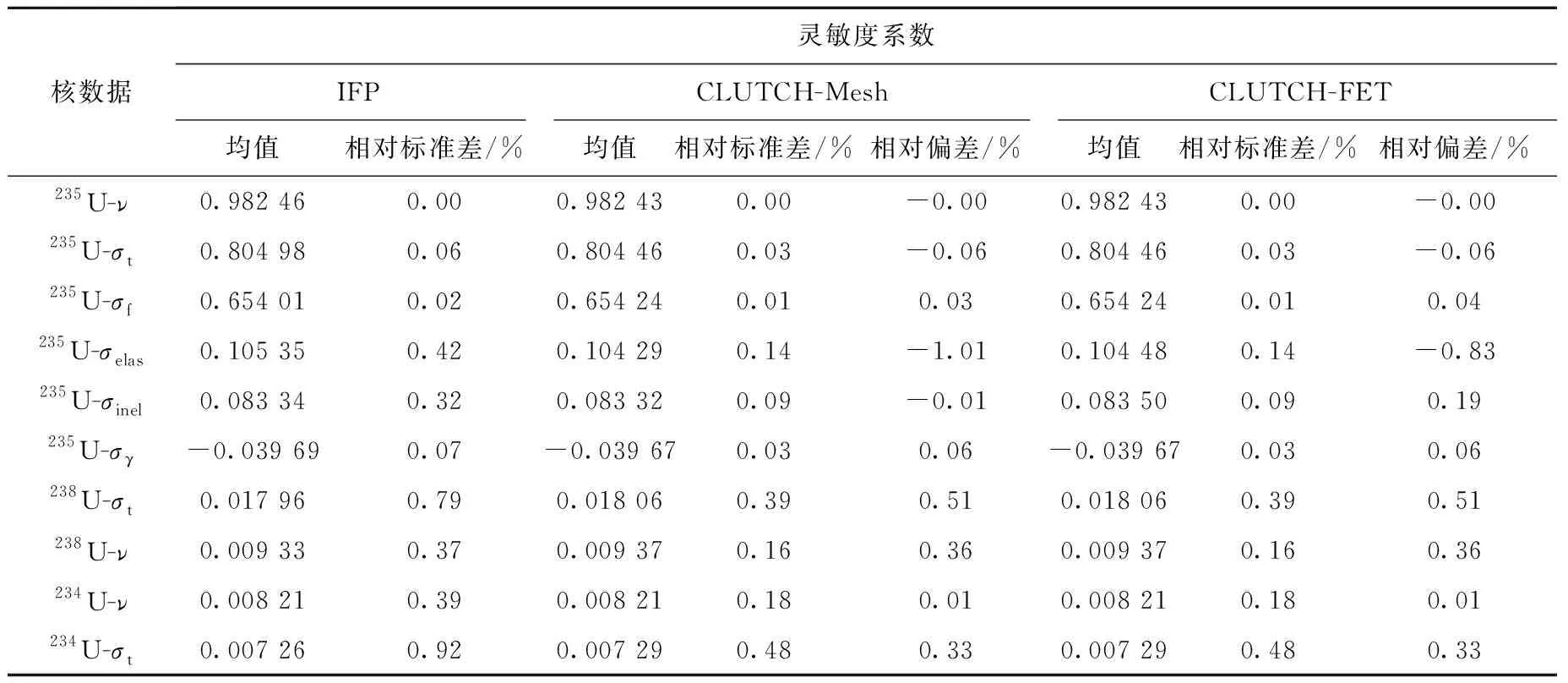
表2 Godiva問題靈敏度系數計算結果Table 2 Sensitivity coefficient result for Godiva problem

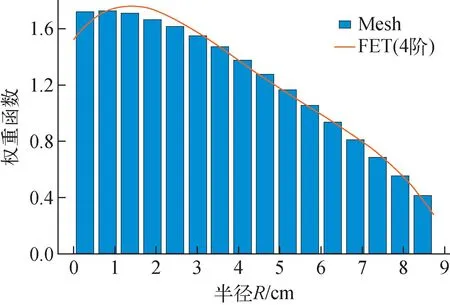
圖3 Godiva問題權重函數分布Fig.3 Distribution of importance weighting functions for Godiva problem

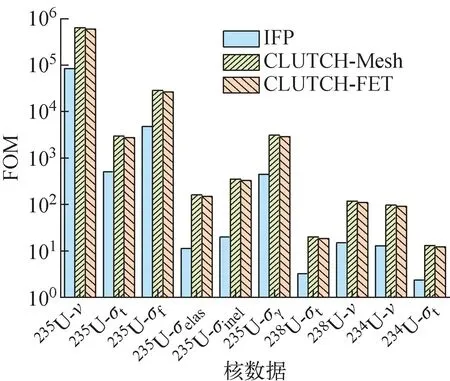
圖4 Godiva問題FOM值對比Fig.4 Comparison of FOM values for Godiva problem

圖3表明,基于網格和基于函數展開計數方法計算得到的權重函數符合得較好,隨著半徑的增大,權重函數的數值逐漸減小。表2顯示,CLUTCH-Mesh和CLUTCH-FET方法的計算結果與IFP方法計算結果的相對偏差基本小于1%,表明了兩種方法的準確性。通過對比圖4所示FOM值,可看出, CLUTCH-Mesh和CLUTCH-FET方法計算得到的靈敏度系數的FOM值相近,CLUTCH-Mesh方法計算得到的FOM值略高于CLUTCH-FET方法,兩種CLUTCH方法的FOM值普遍高于IFP方法,表明CLUTCH-Mesh和CLUTCH-FET方法相比于IFP方法計算效率有較大提升。同一方法、不同核數據的FOM值也有較大差異,這與不同反應道發生的概率有關。

2.2 Flattop問題

Flattop基準題[16]布置如圖5所示,裝置中心材料是钚合金,反射層材料是鈾,堆芯半徑為4.533 2 cm,反射層外徑為24.142 cm。CLUTCH-Mesh方法采用半徑方向均分48份一維球狀網格,CLUTCH-FET方法在半徑方向上全局和分段進行函數展開計數,其中全局函數展開計數表示在半徑方向上對[0 cm,24.142 cm]進行勒讓德函數展開,展開階數分別取5、10、15、20階,分段函數展開計數表示在半徑方向上分別對[0 cm,4.533 2 cm]和[4.533 2 cm,24.142 cm]進行勒讓德函數展開,得到兩套函數展開系數,展開階數均為4階,其他計算參數與Godiva問題相同。得到的權重函數沿半徑的分布如圖6所示,3種方法計算的靈敏度系數列于表3,FOM值示于圖7。

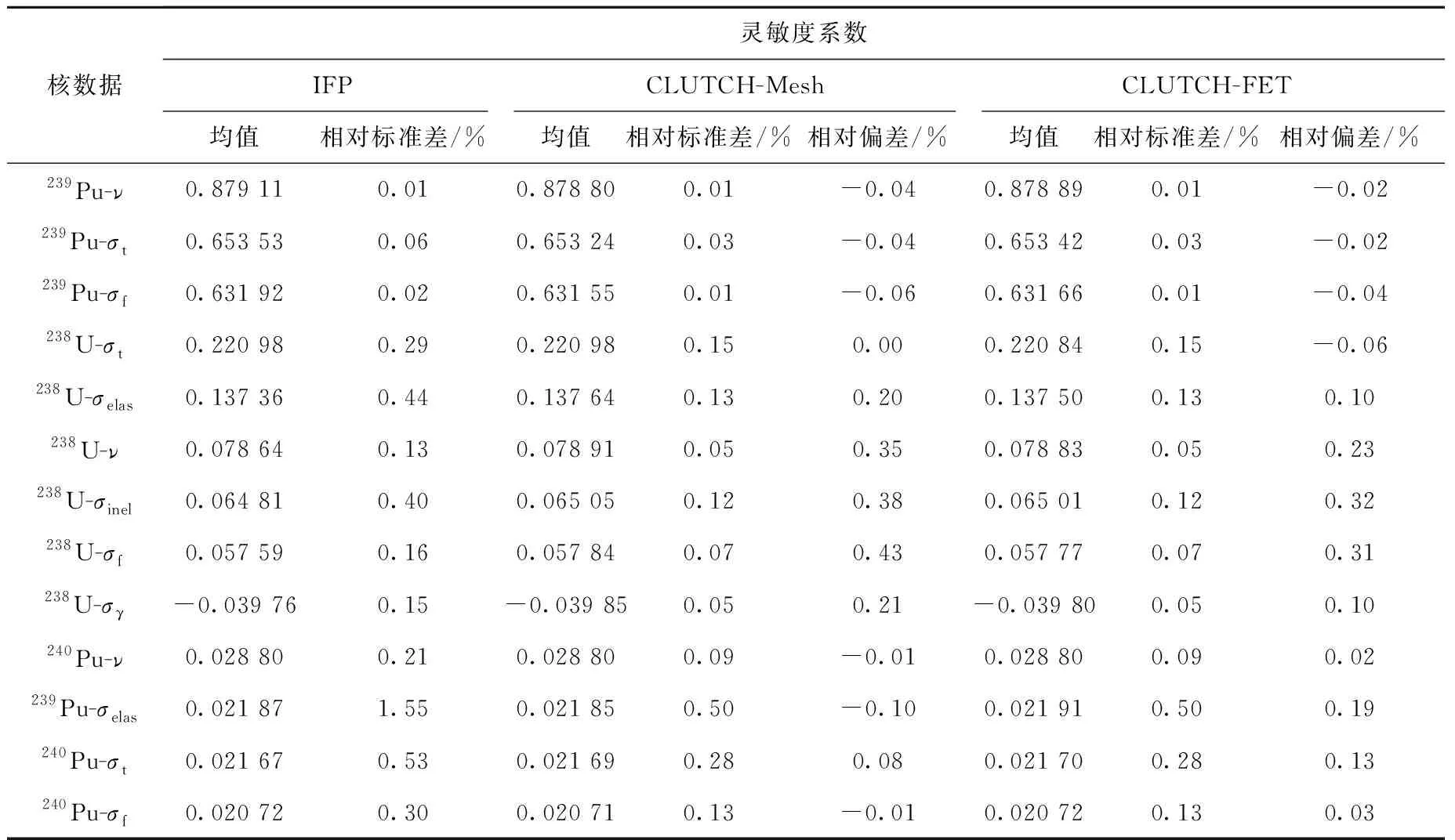
表3 Flattop問題靈敏度系數計算結果Table 3 Sensitivity coefficient result for Flattop problem

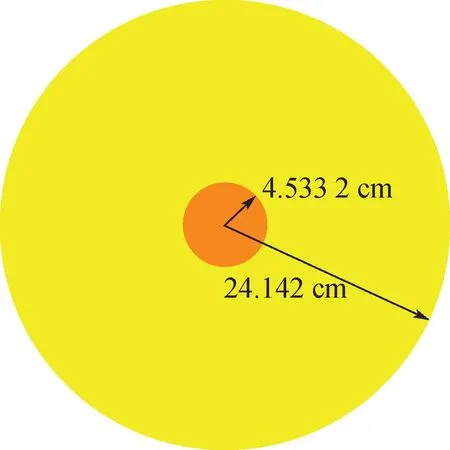
圖5 Flattop基準題Fig.5 Model for Flattop problem

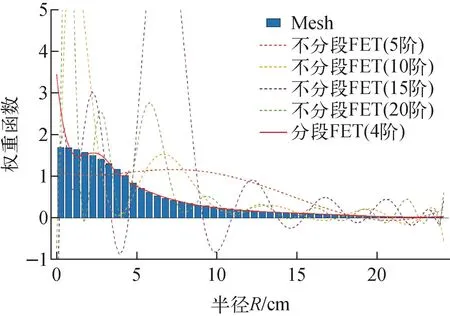
圖6 Flattop問題權重函數分布Fig.6 Distribution of importance weighting functions for Flattop problem

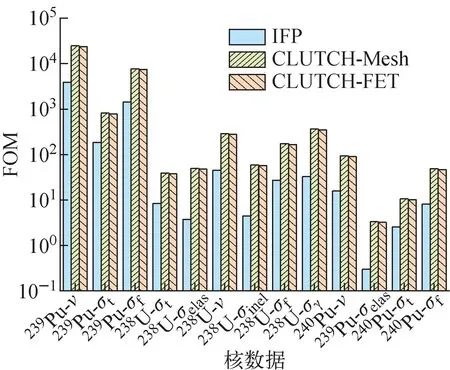
圖7 Flattop問題FOM值對比Fig.7 Comparison of FOM values for Flattop problem

圖6表明,權重函數在半徑方向上的變化達到上百倍,若不進行分段函數展開計數,展開階數取20階,仍無法準確統計出權重函數的分布,因此需要進行分段函數展開計數,才能較好地擬合權重函數的分布。結果顯示,分兩段進行函數展開計數,展開階數取4階時,便可得到較好的權重函數分布結果。因此,當權重函數變化較大時,分段進行函數展開計數較全局函數展開計數的效果更好。一般函數展開計數的分段選在材料分界處,保證每段函數展開計數區域內權重函數的梯度不大,以得到更精確的權重函數。圖6還表明,分段進行權重函數展開計數時,在區間邊界處會出現間斷,但由于權重函數僅在燃料區域有意義,且研究結果[8]表明靈敏度系數的計算對權重函數的精度要求為10%～20%,因此權重函數在區間邊界處的間斷性對靈敏度系數的計算影響較小。由表3可看出,基于CLUTCH-Mesh方法和CLUTCH-FET方法計算的靈敏度系數與IFP結果的相對偏差均小于1%,且兩種方法的計算偏差數值相近,表明兩種方法具有較高的精度且精度相近。圖7表明,基于CLUTCH-Mesh方法和CLUTCH-FET方法計算得到的靈敏度系數的FOM值相近,且普遍高于IFP方法的FOM值,表明兩種CLUTCH方法的計算效率比IFP方法更高。

2.3 AP1000全堆問題

AP1000堆芯布置如圖8所示,采用15×15的燃料布置,共157個燃料組件,控制棒處于全提狀態。在統計權重函數時,CLUTCH-Mesh方法采用340×340×400的立方體網格,以保證網格的大小約為1 cm3,CLUTCH-FET方法對每個燃料組件分別進行函數展開計數,即采用157套函數展開計數,每個燃料組件內,x、y方向各選取4階勒讓德函數展開計數,由于燃料區域的材料在z方向沒有變化,因此在z方向不分段,由于z方向燃料區域較長,適當選取高階展開系數,選取10階勒讓德函數展開計數。每代模擬的粒子數為106,其他計算參數同Godiva問題。IFP、CLUTCH-Mesh和CLUTCH-FET方法計算的靈敏度系數列于表4,FOM值對比示于圖9。

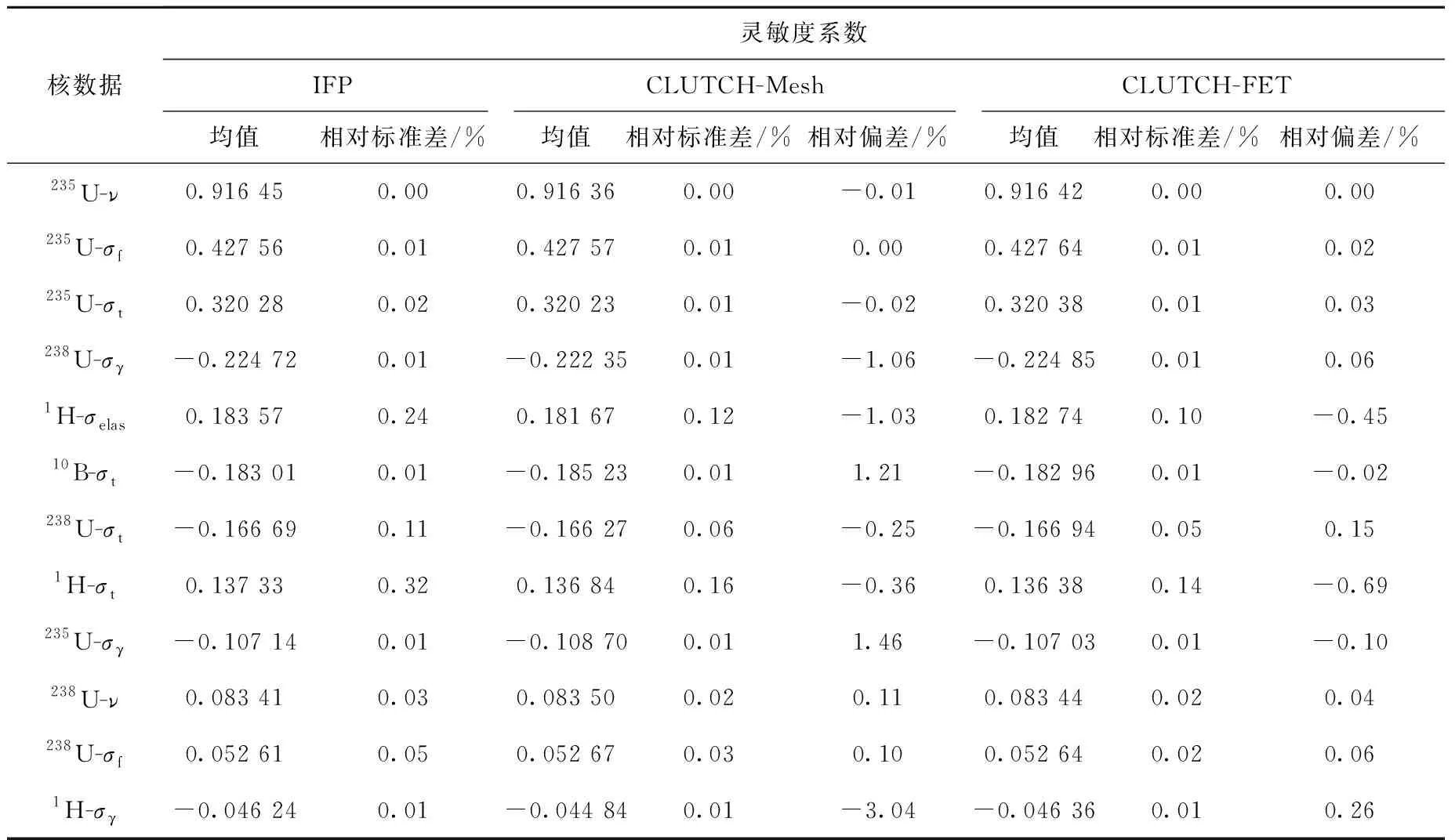
表4 AP1000全堆問題靈敏度系數計算結果Table 4 Sensitivity coefficient result for AP1000 problem

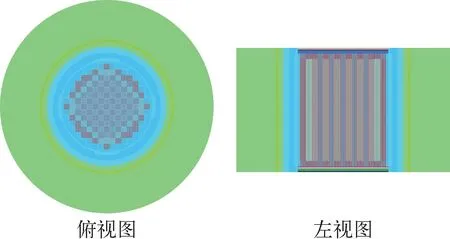
圖8 AP1000堆芯布置Fig.8 AP1000 core layout

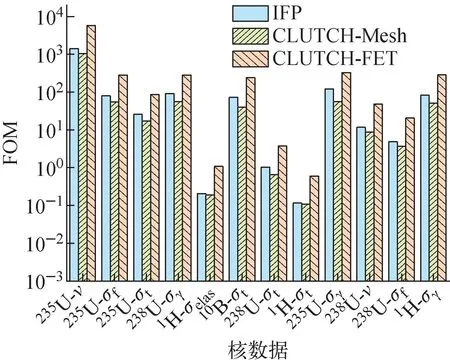
圖9 AP1000問題FOM值對比Fig.9 Comparison of FOM values for AP1000 problem

表4表明,在當前計算條件下,CLUTCH-Mesh方法計算得到的238U-σγ、1H-σelas、10B-σt、235U-σγ和1H-σγ的靈敏度系數的計算相對偏差較大,均大于1%,1H-σγ的甚至達到-3.04%,這是由于AP1000全堆問題規模較大,需要劃分足夠精細的網格才能準確描述權重函數的空間分布,網格數的增多使得每個網格統計得到收斂的權重函數所需的粒子數增多,根據前文結果,在當前網格設置下,每代模擬106個粒子,需要28 581代的非活躍代模擬才能使權重函數收斂,而本次計算僅采用1 000代非活躍代,權重函數未收斂,導致靈敏度系數的計算相對偏差較大。而在當前計算條件設置下,CLUTCH-FET方法計算得到的靈敏度系數的相對偏差均小于1%,表明CLUTCH-FET方法具有較高的精度。對比圖9所示的FOM值,發現CLUTCH-FET方法的FOM值普遍高于CLUTCH-Mesh和IFP方法,CLUTCH-Mesh方法的FOM值最低,這是由于CLUTCH-Mesh方法中網格數達到千萬級別,對于數據量在千萬級別的數組進行規約和運算非常耗時,導致CLUTCH-Mesh方法的FOM值比CLUTCH-FET方法小。相較于IFP方法和CLUTCH-Mesh方法,CLUTCH-FET方法的FOM值分別最大提高了5.2倍和6.0倍。

3 結論

本文分別基于網格和函數展開計數方法對CLUTCH方法中的權重函數進行了統計,函數展開計數選取的基函數為勒讓德多項式,在Godiva、Flattop和AP1000全堆問題上進行了驗證,并將兩種CLUTCH方法(CLUTCH-Mesh和CLUTCH-FET)計算得到的靈敏度系數與IFP方法進行了比較。結果表明,對于Godiva和Flattop問題,CLUTCH-Mesh和CLUTCH-FET方法具有和IFP方法相當的精度,且相較于IFP方法,兩種CLUTCH方法的計算效率有顯著提升。對于AP1000全堆問題,因該問題規模較大,統計權重函數所需的網格數較多,導致權重函數難收斂,從而使得CLUTCH-Mesh方法的計算精度下降,表明CLUTCH-Mesh方法不適用于大規模問題的靈敏度系數求解。而在選取合適的函數展開階數的條件下,CLUTCH-FET方法的計算精度與IFP方法相當,計算效率有所提升,其品質因子較IFP方法最大提高了5.2倍,較CLUTCH-Mesh方法最大提高了6.0倍,表明CLUTCH-FET方法適用于大規模問題的靈敏度系數求解。Flattop問題的權重函數分布結果表明,分段進行函數展開計數的效果較不分段的效果好。