點探測器敏感性關聯抽樣計算方法

李 瑞,付元光,鄧 力,許海波

(1.中物院高性能數值模擬軟件中心,北京 100088;2.北京應用物理與計算數學研究所,北京 100094)

在反應堆輻射屏蔽設計中,常需要通過改變屏蔽體尺寸、材料密度與組分實現屏蔽方案的優化。在此過程中,掌握這些因素導致的輻射劑量率變化規律可有效提高屏蔽方案優化效率。另外,核數據本身的不確定性會對輻射屏蔽模擬結果的準確性造成影響,在屏蔽方案的評估中也需要加以考慮。當不同屏蔽方案的差異較小時,上述計算輻射劑量率變化的問題可視為微擾問題。

反應堆輻射屏蔽模擬一般采用離散縱標(SN)方法與蒙特卡羅(MC)方法。其中SN方法屬于確定論方法,在計算微擾問題時可直接采用兩次獨立計算并做差的方式進行。但是,由于SN方法對于復雜幾何處理能力有限,并存在射線效應等問題,其計算精度一般低于MC方法。與SN方法相比,MC方法可處理比較復雜的幾何體,采用的連續能量核反應截面也更適用于核數據擾動分析。但MC方法的計算量巨大,特別是對于輻射屏蔽這一類深穿透問題,需要使用降方差技巧才能得到統計收斂結果。然而,在微擾問題計算中,由于輻射劑量率本身的改變就很小,如果采用直接MC模擬方法計算,則對于其統計收斂性要求更加苛刻,導致時間開銷進一步增加。因此,為排除隨機漲落的影響,MC方法一般在與參考系統相同的隨機序列下完成微擾系統的模擬,常見的方法包括關聯抽樣[1]與微分算符[2]。

近年來,采用伴隨通量作為重要性的降方差技巧在MC輻射屏蔽模擬中被廣泛研究,如針對單一目標的CADIS算法[3]以及多目標的FW-CADIS算法[4]。這些算法的實質是基于粒子權重的賭/分裂以及偏倚抽樣的組合。另一方面,在MC輻射屏蔽模擬中,常采用點探測器計數方法提高計數率。

MCNP軟件[5]基于微分算符法,提供了體平均通量及其衍生計數的敏感性計算功能。Perel等[6]在此基礎上研究了點探測器計數的敏感性計算方法。與體平均通量這一類徑跡長度估計方法不同,點探測器計數采用了下次事件估計方法[7],需要額外考慮虛粒子的模擬過程。在Perel等[6]展示的算法中,需多次遍歷粒子的徑跡歷史貢獻。在采用權重賭/分裂技巧的屏蔽問題模擬中,次級粒子的數目很多且平均粒子隨機游動鏈較長,這種算法的性能開銷會很大。本工作基于關聯抽樣算法架構,利用單因素擾動系統將系統擾動因素局限在可通過一個擾動權重描述的簡單情形,在此基礎上以隨輸運過程實時更新的方式代替頻繁的粒子歷史遍歷。另外,將擾動權作為粒子擴展屬性也可避免對次級粒子徑跡的回溯需求,從而降低算法的實現難度。

1 算法介紹

關聯抽樣算法的重點在于采用與原系統相同的隨機序列模擬擾動系統的輸運與計數統計過程。在形式上,擾動系統粒子隨機游動過程與原系統是完全相同的,統計差異僅體現在粒子權重上。本工作基于三維粒子輸運模擬軟件JMCT開展算法研究[8]。

對于輻射屏蔽問題,點探測器計數估計量[6]可表示為:

(1)

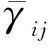
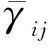
(2)

式中:δ為克羅內克函數,表示僅當虛粒子飛行方向朝向點探測器時觸發計數;Ωd為虛粒子飛行方向矢量;Rd為點探測器的位置矢量;R為隨機游動鏈中粒子的位置矢量;Ps為粒子發生反應時在點探測器方向發射粒子的概率,即指向概率;Σt為總反應截面;s為虛粒子到達探測器過程中經歷的徑跡段長度。

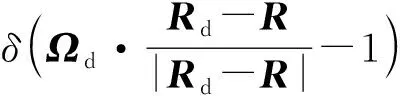
式(1)中的Pik(Ek)為粒子隨機游動鏈中徑跡段的產生概率,按照Perel等[6]對于徑跡段指標的約定,每個徑跡段以碰撞或源抽樣事件開始,因此點探測器計數是在徑跡段開始處觸發的。由于虛粒子與實際碰撞或源抽樣過程是獨立的,因此影響第k個徑跡段點探測器計數的所有徑跡段k∈lin(j)并不包括k徑跡段本身[6]。因此,對于首個點探測器計數,僅依賴徑跡段0,為保證形式上的一致性,將徑跡段指標定義進行簡單擴展,擴展之后的徑跡段概率為:

(3)

Q為輻射屏蔽計算中的外源分布,源粒子的位置屬性指標為0,能量與方向指標為1。由于粒子從R0飛行到R1過程中,其能量與方向是不變的,因此E1與Ω1分別對應了第2個徑跡段開始之前粒子的能量與飛行方向。對于k>1的情況,位置屬性指標與徑跡段的關系以此類推。

T為輸運核,表示粒子飛行至下一次碰撞的概率,其形式為:

T(Rk,Ek,Ωk;Rk-1)=

(4)

Cx為各類反應的碰撞核,如式(5)所示。

Cx(Rk-1,Ek,Ωk;Ek-1,Ωk-1)=

(5)

式中:Σt為宏觀總截面;Σx為宏觀反應截面;νx為反應發生后產生的次級粒子數目,主要用于中子誘發裂變、(n,xn)以及中子產光等反應過程。

(6)

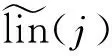
(7)

式(6)所示為權重技巧下的點探測器計數形式。當系統存在擾動時,基于關聯抽樣計算點探測器計數對應變化量Δ(Td)的過程為:

Δ(Td)=Est*[Td]-Est[Td]=

(8)

式中,上標*表示擾動系統相關項。

式(8)對應的隨機游動過程與式(6)類似,唯一的區別就是引入了擾動權乘子

(9)

(10)

(11)

根據式(8)～(11)可構建點探測器擾動量的關聯抽樣算法。僅需要在原系統隨機游動模擬過程中更新并統計擾動權對應的計數即可,算法流程如圖1所示。

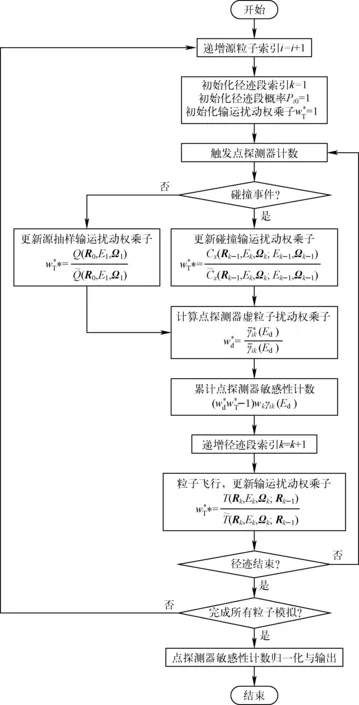
圖1 點探測器擾動關聯抽樣計算流程Fig.1 Flowchart of point detector perturbation based on correlated sampling

另一方面,為完成點探測器擾動的模擬,對于每一個擾動因素,都需要建立與原系統結構相同的統計計數。結構相同是指點探測器的數目、能量區間劃分、時間區間劃分都相同。具有相同結構的擾動系統計數可通過對原系統計數進行克隆得到。所有擾動系統克隆計數的總內存使用量M如式(12)所示。

(12)

式中:Np為擾動系統總數;Nd為點探測器計數數目;Mi為每個點探測器計數的內存使用量。

JMCT中允許在一次模擬中同時分析多個擾動因素,這些擾動因素包括核素截面與材料密度的變化,以及針對擾動因素的能量區間劃分。在本工作中,將某一能量區間內具有單一核素與反應道擾動或材料密度擾動的系統定義為單因素擾動系統。因此,一次MC模擬過程中,可存在多個單因素擾動系統。擾動系統對應的計數內存與內部狀態是獨占的,有效地避免了不同擾動因素在計算流程上相互干擾。對于每個單因素擾動系統,可通過擴展固定數目為1的粒子屬性即可完成輸運擾動權乘子的管理。此外,JMCT允許定義擾動所在幾何體與材料,從而限制擾動的空間范圍。

2 計算結果

利用勞倫斯利弗莫爾國家實驗室(Lawrence Livermore National Laboratory, LLNL)的脈沖球形實驗裝置對算法進行正確性檢驗。該實驗探測D-T脈沖中子在半徑為20.96 cm的石墨球中輸運后的時間泄漏譜,裝置如圖2所示。其中D-T中子源發生器通過孔道經-x方向放置于x=-0.131 cm處。D-T中子能量介于13.20～15.11 MeV區間內,具體分布依賴于出射角度。實驗中,NE-213探測器與-x軸呈30°角,距離石墨球心776 cm。文獻[9]給出了該模型相應的MCNP程序[5]輸入文件。

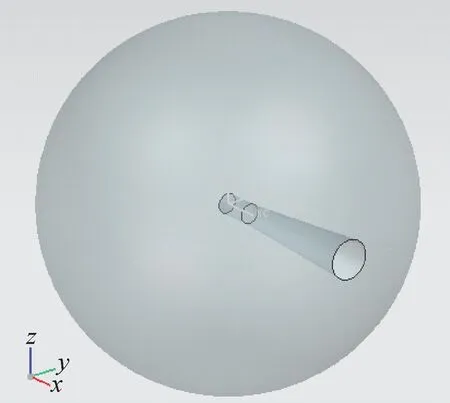
圖2 脈沖球形實驗裝置模型Fig.2 Model of pulsed sphere experiment device

JMCT首先基于該模型進行了泄漏譜的計算,作為對比的實驗值來自文獻[10]。JMCT整體計算結果與Perel等[6]工作符合良好,如圖3所示。

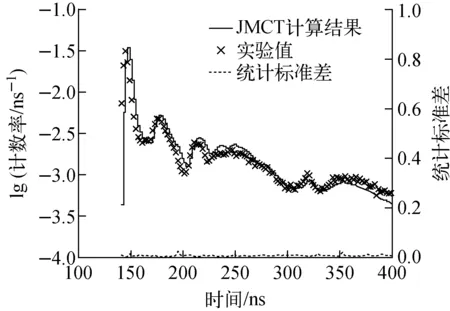
圖3 脈沖球形實驗裝置時間泄漏譜計算結果Fig.3 Calculation result of time leakage spectrum for pulsed sphere experiment device

在此基礎上,對14.918～15.296 MeV區間內的(n,n′1)反應截面引入+1%的擾動,計算時間譜的變化。由于該實驗裝置中D-T中子在石墨球中平均運行2.9個自由程,因此擾動引起的時間泄漏譜變化主要集中在0～2次散射對應的時間區間上。JMCT計算結果如圖4所示。其中由于(n,n′1)反應截面的增加導致擾動系統的總截面變大,進而造成點探測器直穿項計數降低。另外,散射截面的貢獻會由于散射截面的增加而變大,其中一次散射的貢獻最為顯著。將JMCT點探測器直穿項和一次散射峰的變化與Perel等[6]工作中微分算符計算結果進行定量對比,相對偏差均在5%以內,如表1所列。

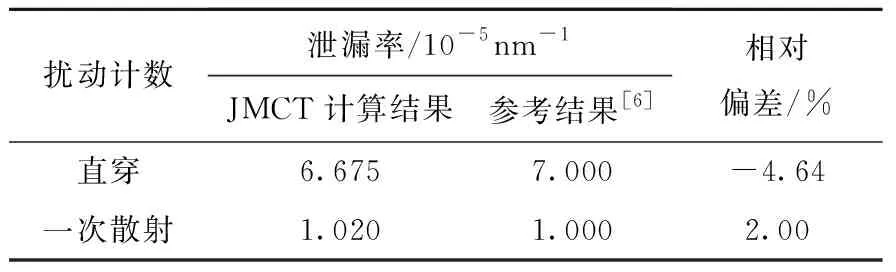
表1 時間泄漏譜擾動結果對比Table 1 Comparison of time leakage spectrum perturbation

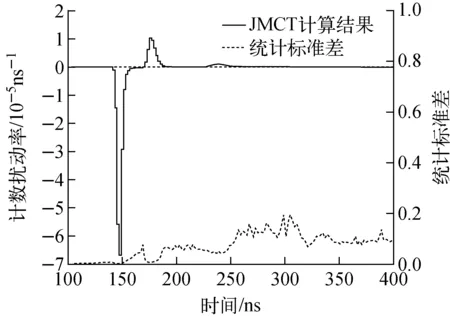
圖4 脈沖球形實驗裝置時間泄漏譜擾動計算結果Fig.4 Calculation result of time leakage spectrum perturbation for pulsed sphere experiment device

針對反應堆輻射屏蔽問題,采用NUREG/CR-6115屏蔽基準題[11]驗證使用降方差技巧的點探測器敏感性計算結果。通過在壓力容器材料中引入+1%的核子密度擾動,計算壓力容器外中子能譜的擾動。為保證計算收斂,該模擬采用了CADIS降方差方法[3],其中伴隨通量來自JSNT[12]計算。在4×108粒子歷史規模下,JMCT壓力容器外表面中子能譜與文獻[11]中的DORT結果對比如圖5所示。

圖5 壓力容器外表面中子能譜計算結果Fig.5 Calculation result of neutron energy spectrum on outer surface of pressure vessel

這里采用直接MC模擬作為參考對比,關聯抽樣的計算結果如圖6所示。結果表明,兩者在趨勢上是符合的,即1～2 MeV能量區間的中子通量下降,而1 MeV能量以下的中子通量增加。導致這一現象的原因主要有2個:一方面是由于壓力容器材料對快中子的慢化作用導致高能中子慢化為低能中子;另一方面,壓力容器內的Fe等核素對快中子的輻射俘獲較低能中子更加顯著。在該算例中,為避免兩次直接MC模擬的統計誤差掩蓋真實擾動,要求各能群統計標準差均低于0.02,兩次MC計算共耗時4 286.2CPU小時,關聯抽樣計算耗時4.1CPU小時。

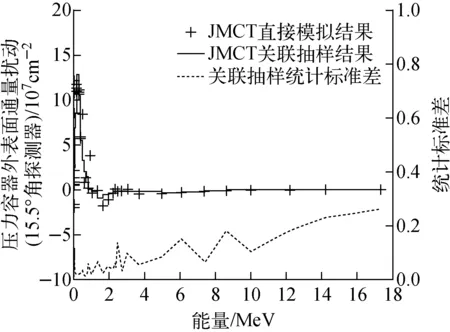
圖6 壓力容器外表面中子能譜擾動計算結果Fig.6 Calculation result of neutron energy spectrum perturbation on outer surface of pressure vessel

3 結論

脈沖球形實驗裝置計算結果表明,基于關聯抽樣的點探測器敏感性計算方法可達到與Perel等[6]工作中微分算符方法相當的計算精度,說明了算法對輸運與計數過程的微擾描述是正確的。在NUREG/CR-6115屏蔽基準題模擬中,CADIS降方差技巧的使用一方面對源抽樣與輸運過程進行了偏倚,另一方面也會在權重輪盤賭過程中產生大量的次級粒子。本工作利用單因素擾動系統的概念將擾動因素進行了規范化,在每個單因素擾動系統內,以粒子擴展屬性的方式實現了擾動權乘子的更新。這一方法解決了權重技巧下輸運與計數過程的微擾描述問題,并且利用次級粒子的存庫與獲取順序避免了敏感性統計中對粒子歷史進行頻繁的回溯,從而降低了算法的運行時間開銷。