項目學(xué)習(xí)中發(fā)展數(shù)學(xué)“三會”
——以“變裝的易拉罐”為例

景昱波, 戴秀梅

(1.杭州市觀成武林中學(xué),浙江 杭州 310000;2.杭州市拱墅區(qū)教育研究院,浙江 杭州 310000)

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2022年版)》提出,在數(shù)學(xué)學(xué)習(xí)過程中,學(xué)生不僅需要獲得“四基”,提升“四能”,還需要培養(yǎng)“三會”的核心素養(yǎng)[1]．核心素養(yǎng)的培養(yǎng)需要教師更新教學(xué)方式,而數(shù)學(xué)項目學(xué)習(xí)正是重要的載體．其以真實問題解決為導(dǎo)向,整合數(shù)學(xué)與其他學(xué)科的知識和方法,讓學(xué)生從數(shù)學(xué)的角度觀察與分析、思考與表達(dá)、解決與闡釋現(xiàn)實生活現(xiàn)象,體會數(shù)學(xué)的價值,發(fā)展應(yīng)用和創(chuàng)新意識．?dāng)?shù)學(xué)項目學(xué)習(xí)的特征可概括為:情境的真實性、問題的挑戰(zhàn)性、過程的完整性、成果的創(chuàng)新性、學(xué)科的融合性[2]．但如何設(shè)計和實施核心素養(yǎng)導(dǎo)向下的數(shù)學(xué)項目學(xué)習(xí),對一線教師來說仍存在困難．

本文基于對核心素養(yǎng)導(dǎo)向下的數(shù)學(xué)項目學(xué)習(xí)的理解,開展案例實踐,并給出相應(yīng)的教學(xué)思考,意在為一線教師的項目學(xué)習(xí)教學(xué)提供借鑒．

1 項目前期分析

1.1 項目內(nèi)容

生活中有兩種不同的易拉罐,二者容量一樣,價格不同,學(xué)生自然會提出驅(qū)動性問題“為什么價格不同”．學(xué)生通過小組交流,自主提出兩個研究思路:1)價格不同可能和包裝用料相關(guān);2)價格不同可能和外觀設(shè)計相關(guān)．在問題的分析與解決過程中,促使學(xué)生將現(xiàn)實生活與數(shù)學(xué)建立聯(lián)系,通過建立數(shù)學(xué)模型來解決問題．本項目融合數(shù)學(xué)、物理、美術(shù)等學(xué)科,以跨學(xué)科的形式進(jìn)行學(xué)習(xí),打破學(xué)科界限,學(xué)生在項目學(xué)習(xí)過程中,完善知識結(jié)構(gòu),提升綜合應(yīng)用能力,從而發(fā)展核心素養(yǎng)．基于以上分析,本項目的教學(xué)重點是:建立現(xiàn)實問題與數(shù)學(xué)的聯(lián)系,利用數(shù)學(xué)建模解決問題．

1.2 學(xué)情分析

本項目實施對象是九年級學(xué)生．在知識能力上,學(xué)生已經(jīng)學(xué)習(xí)過圓、黃金比以及函數(shù)等相關(guān)知識,具備相應(yīng)的基礎(chǔ)知識．在探究能力上,學(xué)生具備合作學(xué)習(xí)的活動經(jīng)驗．但學(xué)生在數(shù)據(jù)測量時不夠嚴(yán)謹(jǐn);在模型推導(dǎo)過程中容易出錯,以及對如何建立模型和研究函數(shù)模型存在疑問．基于以上分析,本項目的教學(xué)難點是:數(shù)學(xué)模型的建立與利用模型分析問題．

1.3 學(xué)習(xí)目標(biāo)

1)通過比較不同易拉罐的價格和外觀,從數(shù)學(xué)角度分析和思考,培養(yǎng)學(xué)生數(shù)學(xué)分析的能力;

2)通過建立數(shù)學(xué)模型和制定假設(shè)解決問題,培養(yǎng)學(xué)生解決問題的能力;

3)通過不斷優(yōu)化模型,對模型的準(zhǔn)確性進(jìn)行評估,培養(yǎng)學(xué)生的實踐意識和反思能力;

4)通過設(shè)計易拉罐的外觀,激發(fā)學(xué)生的創(chuàng)造力和創(chuàng)新思維．

1.4 教學(xué)活動結(jié)構(gòu)設(shè)計

項目學(xué)習(xí)對初中生來說是新鮮的,學(xué)生會懷有很大的熱情,對此教師需要圍繞驅(qū)動性問題和學(xué)習(xí)目標(biāo)制定教學(xué)活動．在教學(xué)活動中應(yīng)鼓勵學(xué)生以小組合作的形式,親歷發(fā)現(xiàn)、提出、分析、解決問題的過程．

本項目的教學(xué)結(jié)構(gòu)如圖1所示:

圖1

2 項目實施過程

2.1 真實情境,問題驅(qū)動

圖2

在超市購買飲料時,可選擇如圖2所示的摩登罐或普通罐,二者飲料容量都是330 ml,而摩登罐(圖2(a))3元/罐,普通罐(圖2(b))2.5元/罐．

問題1通過這個真實情境,你認(rèn)為我們可以研究什么?

師生活動在了解了情境后,自然會提出驅(qū)動性問題“為什么價格不同”.

問題2請同學(xué)們先獨立思考,再以小組討論的方式想想導(dǎo)致二者價格不同的原因.

師生活動學(xué)生通過交流得到2個統(tǒng)一的研究思路(假設(shè)飲料成份相同):

1)價格不同可能和包裝用料相關(guān);

2)價格不同可能和外觀設(shè)計相關(guān)．

教學(xué)說明學(xué)生基于真實情境,自主提出驅(qū)動性問題,這一過程是培養(yǎng)學(xué)生“如何從數(shù)學(xué)的角度發(fā)現(xiàn)和提出問題”的最佳路徑．隨后學(xué)生通過獨立思考與合作交流,進(jìn)一步提出該問題的研究思路,為后續(xù)“如何從數(shù)學(xué)的角度分析問題和解決問題”指明方向．

2.2 問題分析,提出假設(shè)

問題3先從思路“價格不同可能和包裝用料相關(guān)”展開研究,你認(rèn)為怎樣用料會導(dǎo)致價格不同?

師生活動學(xué)生認(rèn)為在容量相同的情況下,可能與用料的材質(zhì)或多少相關(guān)．

教師可組織學(xué)生查閱相關(guān)資料,從資料中可知2種易拉罐的材質(zhì)都是鋁合金,于是確定價格不同可能和材料用量不同相關(guān)．

問題4如何獲得2種易拉罐的鋁合金材料用量?

師生活動師生共同探討,制定方案．

方案1學(xué)生對易拉罐的高、直徑、厚度進(jìn)行測量,分別計算用料體積、質(zhì)量和價格．

方案2學(xué)生通過稱一稱獲得用料的質(zhì)量,計算價格．

2.2.1 方案1的實施過程

追問1在測量的過程中會遇到什么困難?

學(xué)生提出以下困難:

1)易拉罐并非標(biāo)準(zhǔn)圓柱體,在罐身與上下底面連接處存在弧形,且上下底面的形狀不同;

2)易拉罐底面直徑的測量存在難度,需確保所測弦過圓心;

3)易拉罐的厚度不易測量,并且罐身與上下底面厚度不同．

結(jié)合實際情況提出模型假設(shè):

1)假設(shè)2種易拉罐都是圓柱體;

2)假設(shè)易拉罐均由相同的鋁合金材料制作;

3)假設(shè)易拉罐的上下底面都為圓形,且形狀大小無差別;

4)假設(shè)易拉罐罐身的厚度相同,上下底面的厚度相同．

方案1中的符號說明如表1所示:

表1 方案1中的符號說明

教學(xué)說明學(xué)生通過查閱資料明確研究對象．師生共同探討制定2種研究方案．進(jìn)一步,學(xué)生思考方案1數(shù)據(jù)測量過程中的問題,從而提出合理假設(shè),用符號表示,并為后續(xù)建立模型奠定基礎(chǔ)．

問題5結(jié)合大家提出的測量過程中的困難,該如何測量高度、直徑和厚度?

師生活動學(xué)生很容易獲得高度,并通過小組合作獲得了如下4種測量底面直徑的思路:

思路1將罐底描在紙上,利用圓的軸對稱性,對折即可．

思路2利用圓的周長公式C=πd,將紙繞罐身一圈測量周長,求直徑．

思路3利用圓周角定理的推論(90°的圓周角所對的弦為直徑)確定直徑．

思路4利用三角板與直尺制作簡易卡尺,測量直徑．

最終通過查閱文獻(xiàn)資料獲得易拉罐的制作工藝和材料厚度．

方案1中的數(shù)據(jù)結(jié)果如表2所示:

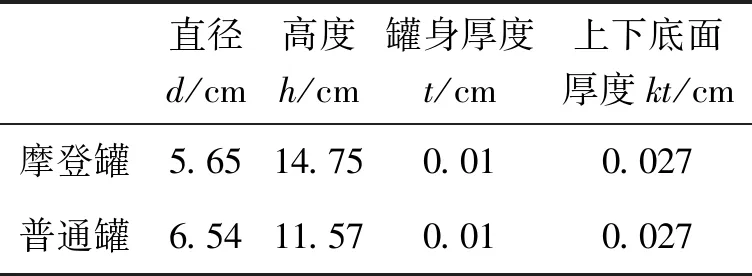
表2 方案1中的數(shù)據(jù)結(jié)果

模型建立由圓柱體的底面半徑r、高h(yuǎn)、罐身厚度t、上下底面厚度kt,計算用料體積

V=2πr2kt+2πrht;

(1)

由鋁合金的密度ρ,計算制作用料質(zhì)量

m=ρV;

(2)

最后結(jié)合鋁合金的單價P,可得用料總價

W=Pm.

(3)

問題6在利用模型解決問題前,還需要什么數(shù)據(jù)?

師生活動學(xué)生查閱資料可得鋁合金密度為2.7 g/cm3,單價為25元/kg．

學(xué)生將數(shù)據(jù)代入模型,結(jié)果如表3所示:

表3 代入模型后的結(jié)果

2.2.2 方案2的實施過程

學(xué)生通過稱重,得到數(shù)據(jù)結(jié)果如表4所示:

表4 方案2的數(shù)據(jù)結(jié)果

結(jié)論1普通罐的鋁合金用料價格反而比摩登罐的高,可知摩登罐比普通罐定價高和用料無關(guān)．

教學(xué)說明本環(huán)節(jié)是對研究思路1的探究．學(xué)生通過查閱資料或是小組討論獲得數(shù)據(jù),通過數(shù)學(xué)模型得到摩登罐比普通罐定價高和用料無關(guān)的結(jié)論．教師在教學(xué)過程中需通過有效問題進(jìn)行引導(dǎo),并給學(xué)生思考與交流的時間,學(xué)生定將還教師無限的可能．

2.3 優(yōu)化模型,解決問題

問題7再從“價格不同與外形設(shè)計理念相關(guān)”展開研究,摩登罐的設(shè)計特殊在哪里?

師生活動學(xué)生通過獨立思考與小組交流,獲得如下2種想法:

想法1摩登罐的長、寬比例更加協(xié)調(diào),符合大眾的審美.

想法2由于摩登罐的用料比普通罐少,說明在材料的利用率上更高．

問題8結(jié)合所測數(shù)據(jù),思考摩登罐的長、寬比例為何更加協(xié)調(diào),其背后是否蘊(yùn)含數(shù)學(xué)知識?

問題9能否利用數(shù)學(xué)知識說明摩登罐的設(shè)計材料利用率更高?

師生活動利用所測數(shù)據(jù),計算發(fā)現(xiàn)摩登罐的實際容量L1=370 ml,而普通罐的實際容量L2=389 ml.因此,摩登罐的空間利用率高于普通罐．

追問2當(dāng)摩登罐的實際容量固定時,易拉罐的高度h與底面半徑r是否具有函數(shù)關(guān)系?

追問3能否將模型(1)轉(zhuǎn)化成V關(guān)于r的函數(shù)模型?利用函數(shù)模型說明摩登罐的設(shè)計更有優(yōu)勢.

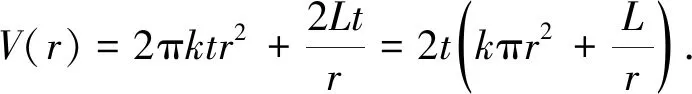
(4)

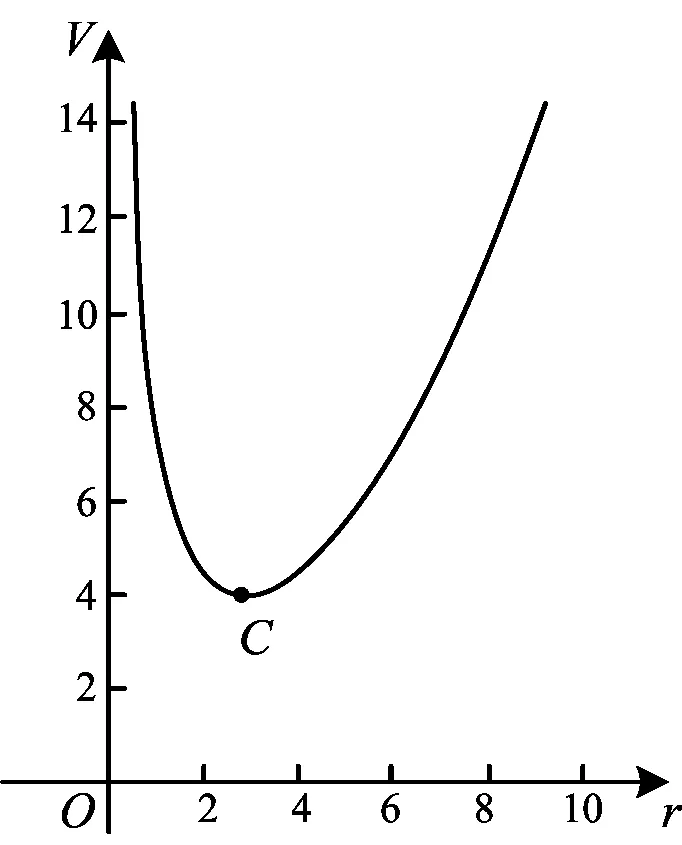
圖3

將摩登罐的數(shù)據(jù)帶入函數(shù)模型,學(xué)生利用GeoGebra軟件繪制函數(shù)圖象(如圖3),并找到相應(yīng)的極值點C的橫坐標(biāo)為r=2.794,可知其近似等于摩登罐的半徑2.825,因此摩登罐的設(shè)計是在以實際容量為370 ml基礎(chǔ)上的最優(yōu)設(shè)計．

教師可適當(dāng)普及高中知識,利用導(dǎo)函數(shù)得到極值點的橫坐標(biāo)．對原函數(shù)求導(dǎo)可得

利用摩登罐的數(shù)據(jù)驗證:摩登罐在實際容量為370 ml且k=2.7時,最優(yōu)解為r=2.794,h=15.08,這與實際r=2.825,h=14.75接近,因此摩登罐的設(shè)計符合最優(yōu)尺寸設(shè)計．

結(jié)論2摩登罐不僅設(shè)計理念與黃金比相關(guān),且在用料上少于普通罐,材料利用率和空間利用率更高.利用函數(shù)模型也可求得摩登罐的設(shè)計接近最優(yōu)尺寸設(shè)計,設(shè)計理念更加環(huán)保．因此,師生一致認(rèn)為摩登罐定價高,是因為隱藏其中的設(shè)計價值.

教學(xué)說明本環(huán)節(jié)是對研究思路2的探究．學(xué)生思考交流得到2種想法,通過分析測量數(shù)據(jù)發(fā)現(xiàn)設(shè)計理念與黃金比相關(guān);再從材料利用率著手,將已有模型轉(zhuǎn)化成函數(shù)模型,運用軟件繪制函數(shù)圖象,研究函數(shù)性質(zhì),符合函數(shù)學(xué)習(xí)的一般思路,真正做到學(xué)以致用;隨后教師立足高觀點,利用函數(shù)模型分析最優(yōu)設(shè)計,并驗證摩登罐接近最優(yōu)設(shè)計．在教學(xué)過程中教師需引導(dǎo)學(xué)生解釋數(shù)學(xué)結(jié)論的現(xiàn)實意義,從而解決驅(qū)動問題．

2.4 交流展示,遷移應(yīng)用

為了進(jìn)一步鞏固項目學(xué)習(xí)中獲得的經(jīng)驗與方法,將成果進(jìn)行課后延伸,教師需要布置與項目學(xué)習(xí)相關(guān)的子任務(wù)給學(xué)生課后研究學(xué)習(xí)．本項目教師給出了2個子任務(wù)“黃金比在生活中的應(yīng)用”與“能否設(shè)計一款300 ml液體容量的易拉罐使得材料最省”,這2個子任務(wù)的完成有助于提升學(xué)生綜合素養(yǎng)和數(shù)學(xué)建模的能力,發(fā)展創(chuàng)新意識與應(yīng)用意識．

子任務(wù)1的交流展示學(xué)生自主完成“黃金比在生活中的運用”作業(yè),并組織班級內(nèi)交流展示．發(fā)現(xiàn)黃金比主要涉及以下內(nèi)容:

1)人體結(jié)構(gòu).人體結(jié)構(gòu)中有許多比例關(guān)系接近0.618,如人有20顆乳牙、32顆恒牙,其比例接近黃金比;人的正常體溫37℃,而人在24℃的環(huán)境下新陳代謝和生理機(jī)能都處于最佳狀態(tài),其比例也接近黃金比．

2)自然現(xiàn)象.有些植莖上,2張相鄰葉柄的夾角是137°28′,圓周是360°,360°-137.5°=222.5°,而137.5∶222.5≈0.618,研究發(fā)現(xiàn),這種角度對植物通風(fēng)和采光效果最佳．

3)藝術(shù)創(chuàng)作.西方藝術(shù)家非常注重把和諧的比例關(guān)系融入藝術(shù)作品中.例如,名畫《蒙娜麗莎的微笑》《維特魯威人》.又如,著名的雕塑《維納斯》《大衛(wèi)》．

4)建筑設(shè)計.帕特農(nóng)圣廟的外部建筑結(jié)構(gòu)完全按照黃金矩形設(shè)計,給人莊嚴(yán)肅穆的感覺和美的享受.埃及金字塔、上海東方明珠塔、埃菲爾鐵塔等都符合黃金比例.

5)工業(yè)設(shè)計.以logo設(shè)計為例,許多品牌的標(biāo)志均利用黃金圓環(huán)進(jìn)行設(shè)計,如蘋果手機(jī)、麥當(dāng)勞等.

子任務(wù)2的遷移應(yīng)用學(xué)生在研究子項目2“能否設(shè)計一款300 ml液體容量的易拉罐使得材料最省”時自主提出了以下3個問題:

1)為什么易拉罐的設(shè)計都是圓柱形的,而非立方體形狀?

2)為什么易拉罐的實際容量要高于液體容量?

3)如果采用更先進(jìn)的制作材料和工藝,會不會用料更省?

評注采取小組合作的形式展開交流:對于問題1),從數(shù)學(xué)角度可知,平面中等面積情況下,圓的周長最小,于是在等體積的柱體情況下,橫截面為圓形用料最少;從物理角度可知,易拉罐多數(shù)裝碳酸飲料,當(dāng)受到外力時,圓形的表面受力均勻,不易變形,方便運輸．

對于問題2),碳酸飲料在運輸過程中,搖晃會產(chǎn)生膨脹,為其預(yù)留一定的氣體空間較為合理,這也是為何易拉罐實際容量要大于液體容量的原因．

學(xué)生選擇不同容量的易拉罐,通過數(shù)據(jù)計算或測量(見表5),得到至少預(yù)留液體容量的10%比較合理．

表5 不同容量的易拉罐的相關(guān)數(shù)據(jù)

因此,模型優(yōu)化為

對于問題3),學(xué)生通過查詢文獻(xiàn)資料,獲知現(xiàn)在國際上最先進(jìn)的制作工藝的鋁材厚度為0.254mm．

將數(shù)據(jù)代入優(yōu)化后模型可得

圖4

利用GeoGebra軟件繪制函數(shù)圖象(如圖4),獲得極值點的橫坐標(biāo)r≈2.74．

教學(xué)說明學(xué)生課后進(jìn)一步研究學(xué)習(xí),逐漸產(chǎn)生富有創(chuàng)造性的想法,并形成獨創(chuàng)性的項目成果．不僅有對于黃金比在生活中的運用的研究報告,還有對于模型的遷移運用,這些創(chuàng)造性成果不僅促進(jìn)了學(xué)生對項目的深度理解,還豐富了項目學(xué)習(xí)的評價方式．

3 若干反思

研究表明數(shù)學(xué)項目學(xué)習(xí)對于學(xué)生數(shù)學(xué)知識的學(xué)習(xí)以及非智力層面均有積極意義,但對于課堂教學(xué)以及教師自身都提出了一定的挑戰(zhàn),從而引發(fā)了相關(guān)思考．

3.1 關(guān)于項目學(xué)習(xí)與傳統(tǒng)課堂教學(xué)關(guān)系的思考

數(shù)學(xué)項目學(xué)習(xí)是以真實情境為背景、以項目任務(wù)來推動學(xué)習(xí),數(shù)學(xué)知識的學(xué)習(xí)貫穿其中,即前者是“明線”,后者是“暗線”．研究表明,它為學(xué)生的思考與探究提供了學(xué)習(xí)環(huán)境,“做中學(xué)”更能凸顯數(shù)學(xué)與生活的聯(lián)系,從而加深知識的理解,發(fā)展核心素養(yǎng)．但是數(shù)學(xué)知識之間是具有內(nèi)在聯(lián)系的,而非項目學(xué)習(xí)中相對零散的數(shù)學(xué)知識．從核心素養(yǎng)角度來看,模型觀念、數(shù)據(jù)觀念、應(yīng)用意識、創(chuàng)新意識的確在項目學(xué)習(xí)中能夠得到較好的發(fā)展,但是抽象能力、運算能力、幾何直觀、推理能力這類高層次學(xué)科素養(yǎng)難以適應(yīng)這種活潑的教學(xué)形式,日常授課更需要傳統(tǒng)的課堂教學(xué)．因此,項目學(xué)習(xí)不是對傳統(tǒng)課堂教學(xué)的一種顛覆,而是一種很好的補(bǔ)充．

3.2 關(guān)于項目學(xué)習(xí)中教師自身的思考

項目學(xué)習(xí)對教師提出了更高的要求,在傳統(tǒng)課堂中教師更多的是知識的傳授者,而在項目學(xué)習(xí)中教師還是項目的設(shè)計者和學(xué)生研究的促進(jìn)者、合作者．由于數(shù)學(xué)項目學(xué)習(xí)往往是以跨學(xué)科的形式呈現(xiàn),因此需要教師具有更多的知識儲備與更高的科研能力．項目學(xué)習(xí)的設(shè)計先要挑選真實情境下合適的主題,并以核心素養(yǎng)為導(dǎo)向設(shè)計教學(xué)目標(biāo),再基于學(xué)情設(shè)計具有一定開放性、指向不同水平層次的驅(qū)動性問題,結(jié)合驅(qū)動問題與教學(xué)目標(biāo)設(shè)計師生協(xié)作的教學(xué)活動,最后還需要設(shè)計“全程式”的評價體系．面對如此巨大的挑戰(zhàn),教師要提升學(xué)習(xí)能力與合作意識,一方面,積極參加各類數(shù)學(xué)項目學(xué)習(xí)的培訓(xùn),充分利用各種資源,提升理論基礎(chǔ)與實踐經(jīng)驗;另一方面,加強(qiáng)學(xué)科間教師交流,集團(tuán)隊的力量開發(fā)高質(zhì)量的項目學(xué)習(xí)課程,從而真正通過項目學(xué)習(xí)發(fā)展核心素養(yǎng)．