基于相場模型的再生冷卻推力室熱機疲勞壽命分析

孫 燊 易 敏

(南京航空航天大學 航空航天結構力學及控制全國重點實驗室,江蘇 南京 210016)

0 引言

可重復使用運載器具有高效、經濟、環保等特點,是目前航天技術發展的重要方向[1]。2015年以來,美國私人航天公司SpaceX回收并重復使用獵鷹9號運載火箭,國外研究機構不斷突破,以求擺脫單次使用運載火箭高昂費用對空間探索的制約。我國一方面密切追蹤國外先進技術發展[2-3],另一方面努力推進自身關鍵技術攻關。可重復使用運載器技術既能降低空間運輸成本,貫徹可持續發展戰略,又是彰顯綜合國力、搶占空間優勢的必要工具。液體火箭發動機作為動力裝置,其耐久性和可靠性是保障運載器可重復使用的關鍵。推力室喉部結構是液體火箭發動機的核心部件,在服役過程中會經歷復雜、交變的熱機載荷作用,不均勻的溫度分布、局部的塑性應變更會加快結構的疲勞失效。因此,對推力室喉部結構進行傳熱分析和疲勞壽命預測具有重要意義。

推力室在工作時會經歷急速的升溫與降溫,在局部會發生較大的熱變形,分析結構承受的熱載荷需要計算結構的傳熱情況和溫度分布。推力室內壁需要承受高溫燃氣的沖刷作用,冷卻劑在冷卻通道中逆流降溫。多種材料分別具有不同的物性,對傳熱分析的計算結果提出很高的要求。吳峰等應用湍流模型進行了三維數值模擬,計算了再生冷卻推力室通道的流動與傳熱[4]。韓煒對推力室的再生冷卻情況進行了三維數值模擬,得到了內壁面上溫度分布一般規律[5]。吳有亮等提出了推力室準二維傳熱計算的通用方法,相較于三維計算,降低了計算時間,極大地提升了計算效率[6]。根據傳熱分析得到的溫度分布可以計算結構中的熱本征應變,可仿真模擬燃氣溫度和燃氣壓強載荷的共同作用效果,并預估推力室使用壽命。孫冰等對推力室結構進行了三維瞬態熱分析,并根據應力應變分布預測了結構危險點的失效情況[7-9]。徐紹桐等建立了推力室壁在燃氣/冷卻液溫度和燃氣壓強載荷下的二維彈塑性計算模型,提高了失效行為模擬的計算速度[10]。張明等通過數值計算研究了變截面冷卻通道的傳熱情況[11]。目前,推力室疲勞壽命預測的研究主要是基于損傷力學計算損傷的累積,或者根據應力-應變法計算材料的疲勞壽命,較少從斷裂力學出發預測壽命。

傳統方法處理斷裂問題往往將界面作為一個突變的量來處理,突變問題的數值奇異性增加了問題的求解難度。在材料斷裂的界面,數值上難以進行微分算法,材料參數需要考慮因材料破壞而損失的剛度。相場模型通過引入在界面處急劇變化但連續的相場變量——序參量來描述不同的相[12-14],斷裂序參量在整個計算區域上是連續變化的,因此相場模型中不再需要采用特殊的數學方法追蹤界面的幾何形態,也避免了追蹤斷裂面所引起的誤差。相場斷裂方法可以反映加載過程中斷裂序參量的演化,直觀地觀察到裂紋的演化。Francfort等[15]通過對Griffith斷裂理論[16]及變分公式的研究,提出了準靜態脆性斷裂的相場模型。Miehe等提出了應變張量的譜分解方法,用以區分壓縮和拉伸對應的應變能,并且推廣到熱-彈-塑性耦合的斷裂問題[17-19]。文獻[20-21]通過修正斷裂相場模型中的斷裂韌性,實現對疲勞斷裂問題的相場模擬。

本文使用相場疲勞斷裂模型對再生冷卻推力室喉部結構進行有限元模擬,通過熱傳導方程考慮溫度載荷引入的熱本征應變,得到結構的溫度和應力/應變分布情況,根據相場序參量的變化分析結構的疲勞斷裂過程,研究推力室結構在服役過程中的失效行為和熱機疲勞壽命。

1 熱力耦合疲勞相場模型

1.1 熱力耦合模型

銑槽式再生冷卻推力室采用等肋寬的薄壁結構,其喉部自內向外分別為內壁、冷卻通道和外壁,冷卻通道使用肋片進行強化傳熱。推力室中實際發生的熱量傳遞包括:燃氣對內壁的加熱、冷卻劑對冷卻通道的對流換熱。考慮熱載荷對受力的單向耦合,采用穩態熱平衡方程對溫度場進行傳熱分析,熱傳導的控制方程為無熱源的導熱微分方程,即

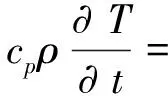
(1)

式中:cp為定壓比熱容;ρ為材料密度;T為結構溫度;t為時間;?為哈密頓算子;λ為材料熱導率。

發動機推力室在工作過程中同時受到溫度載荷和機械載荷的作用。結構的總應變εtotal由熱應變εth、彈性應變εela、塑性應變εpla和蠕變應變εcr構成,即

εtotal=εth+εela+εpla+εcr

(2)

熱應變與溫度的變化成線性關系,即

εth=αthΔTI

(3)

式中:αth為線膨脹系數;ΔT為相對參考溫度的溫度變化量;I為二階單位張量。

1.2 塑性模型

在分離彈性應變和塑性應變時,使用von Mises屈服準則來判斷材料是否達到屈服,屈服條件表達式為

(4)

式中:f為屈服函數;s為偏應力張量;a為背應力張量,即屈服面中心;σy為屈服應力。

達到屈服面后塑性應變產生,塑性應變沿著屈服面梯度方向增加,即

(5)

式中:dλ為塑性乘子,即等效塑性應變增量;σ為應力張量。

1.3 蠕變應變模型

計算蠕變應變時,考慮陳化理論,即Norton定律。在蠕變過程中,時效、擴散和恢復等因素影響蠕變行為,其中時間是最大的影響因素。Norton模型的表達式為

(6)

1.4 斷裂相場模型

定義相場序參量c表示材料的斷裂情況,如果材料完好未損壞,則c為 1;如果存在裂紋,則c為 0。因此,變量c可以看作是損傷力學模型中的損傷參數。斷裂模型中總自由能密度由彈性應變能、塑性應變能和斷裂界面能組成,表達式為

ψ=ψela+(1-c)2ψpla+ψc

(7)

假定彈性應變中只有拉伸分量驅動裂紋擴展,將彈性應變譜分解為

εela=PΛPT

(8)

式中:Λ=diag(λ1,λ2,λ3)是與彈性應變張量相似的對角陣,λ1、λ2、λ3為彈性應變的特征值;P為特征矩陣。

根據譜分解,彈性應變的正負分量為

εela+=PΛ+PT

εela-=PΛ-PT

(9)

彈性應變能密度分解為驅動裂紋擴展的拉伸部分ψela+和不可驅動裂紋擴展的壓縮部分ψela-,表達式為

(10)

根據Borden的塑性斷裂相場模型[22],塑性應變能密度表達式為

(11)

裂紋的相場演化方程表示為

(12)

式中:η為動力學系數;l0為界面寬度尺寸;G為臨界斷裂能密度;ψh為驅動裂紋擴展的歷史變量,即

(13)

1.5 考慮疲勞的相場模型

推力室結構在工作過程中會經歷周期性的熱應力或熱應變,單次循環載荷作用下,應力水平可能遠低于使材料斷裂的臨界應力,但是仍會經歷往復循環的塑性變形。因此,需要考慮循環載荷下的相場疲勞斷裂模型。通過引入疲勞退化函數,對材料的斷裂韌性進行修正,使其在循環載荷下不斷衰減,模擬結構在疲勞載荷下的斷裂失效。采用的退化函數為

(14)

(15)

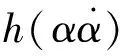
(16)

疲勞斷裂的相場演化方程表示為

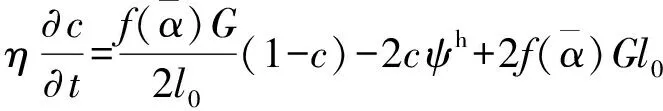
(17)

2 計算結果與討論

推力室喉部為環形對稱結構,選取1/2冷卻再生通道截面作為計算模型,結構的幾何特征與邊界條件如圖1所示。

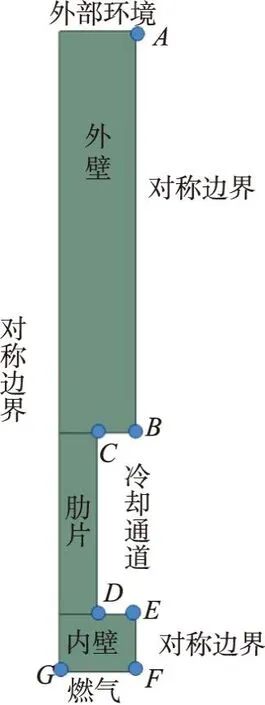
圖1 模擬結構幾何示意圖Fig.1 Geometry of the structure

本文在 MOOSE(Multiphysics Object-Oriented Simulation Environment)框架下進行模擬,通過編寫有限元程序,利用PETSc求解器和Libmesh庫進行并行計算。為了提高計算效率,使用二維平面應變結構進行模擬。本文采用四邊形網格進行網格劃分。模型網格基礎尺寸為0.1 mm,在肋片和內壁進行加密,尺寸最小為0.01 mm,網格數量為16 305。對于網格無關性驗證,進行了6 495、16 305和29 888不同單元數量的測試,3種網格的溫度分布基本一致,第一種網格與后兩種網格所獲得的應力/應變分布有明顯差別,后兩種網格所獲得的結果基本一致,故本文結果皆是基于第二種網格(16 305單元)得到的。計算采用單向耦合求解,在每一個時間步,先進行傳熱計算,得到溫度分布后,將溫度轉化為熱應變,代入力學方程求解應力/應變和斷裂相場值,然后進行下一時間步的計算。模型的兩邊設置為對稱邊界。發動機工作過程分為啟動-熱試車-后冷-關機4個階段,各階段時長分別為5、300、20、600 s,環境溫度為295.15 K。結構的溫度邊界條件和壓力邊界條件參見文獻[23]。

結構的內壁和肋片材料為NARloy-Z銅合金,外壁材料為1Cr21Ni5Ti。NARloy-Z銅合金性能參數參照Esposito 在高低溫環境下的單軸拉伸試驗數據[24],蠕變模型使用Ellis得到的不同溫度、不同應力水平下的蠕變試驗數據[25]。相場疲勞斷裂模型的參數見表1。為了獲得相場模型參數,根據材料的屈服強度、抗拉強度和伸長率等參數先進行不同參數下的單軸拉伸計算測試,選取能實現吻合實驗結果的模型參數,再進行推力室受載計算。

表1 NARloy-Z合金參數Tab.1 Parameters of NARloy-Z alloy

2.1 溫度分布結果

不同階段下結構的溫度分布如圖2所示。在熱試車階段,結構的升溫比較明顯,最高溫度出現在內壁下表面,G點溫度最高可達881.17 K。

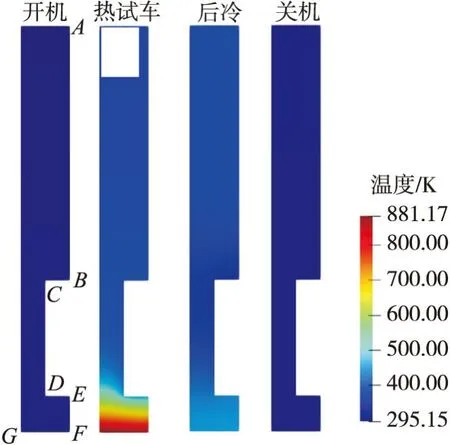
圖2 各階段溫度分布Fig.2 Temperature distribution at different stages

選取結構上7個參考點的溫度變化曲線,如圖3所示。可以看出:自下而上,內壁溫度最高,肋片次之,外壁溫度最低。由于內壁與肋片的材料熱導率高于外壁,外壁上參考點的升溫速率也明顯慢于其他兩部分。外壁上B、C兩點的溫度基本一致。

圖3 各參考點溫度變化Fig.3 Temperature evolution of reference points

2.2 單次工作結構應力/應變分析

推力室單次工作各階段結構的應力/應變分布如圖4和圖5所示。在開機階段,結構升溫幅度較小,整體的壓應力和壓應變的數值較低。由于肋片膨脹受到內、外壁的限制,整體處于壓應力水平。在熱試車階段,結構整體升溫,受熱膨脹,由于受到對稱邊界的限制,結構整體表現為受壓。肋片膨脹受到外壁限制,C處會產生較高的壓力。該階段下,結構內壁下表面溫度最高,G點受到左側邊界的限制,受到的壓應變最大,最高達到1.34%。在后冷階段,結構彈性變形恢復,內壁由于壓載較大,降溫后有殘余的塑性變形。內壁下表面F點和G點分別表現為殘余拉應變和殘余壓應變。F點受到拉伸載荷,殘余應變約為1%。在關機階段,結構的溫度分布與后冷階段相差不大,結構最終的受載情況和殘余應變與后冷階段基本一致。

圖4 各階段應力分布Fig.4 Stress distribution at different stages

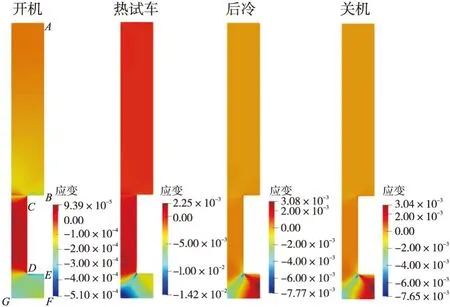
圖5 各階段應變分布Fig.5 Strain distribution at different stages

根據應力和應變分布圖,確定D、E、F、G這4點在工作過程中受到的局部應力-應變較大,為服役危險點。這4點的應力、應變曲線如圖6所示。4個點在循環中都經歷壓應力變為拉應力,D、E、G點始終受到壓應變,F點最終由壓應變轉變為拉應變。

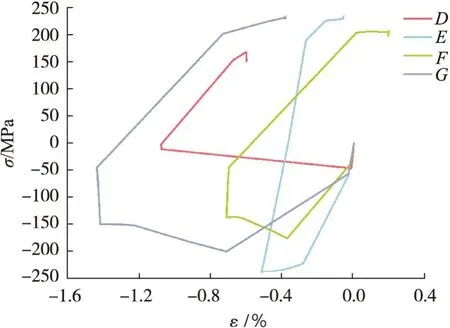
圖6 單次工作中4個特征點的應力-應變曲線Fig.6 Stress-strain curves of four points during single cycle

2.3 10次循環結構應力/應變分析

對10個工作循環下的推力室喉部結構進行仿真。根據單次循環應力應變分析,結構的危險點位于內壁下表面的F和G點,循環仿真后重點關注F和G點的應力應變情況。F點和G點10次循環的應力應變曲線分別如圖7和圖8所示。隨著循環數的增加,F、G兩點表現為應力控制的非對稱循環加載,并且每次循環結束殘余應變值不斷增加。其中,F點為拉伸應變,G點為壓縮應變。F、G兩點殘余應變發展曲線如圖9所示。

圖7 F點10次循環應力-應變響應Fig.7 Stress-strain response of point F in 10 cycles

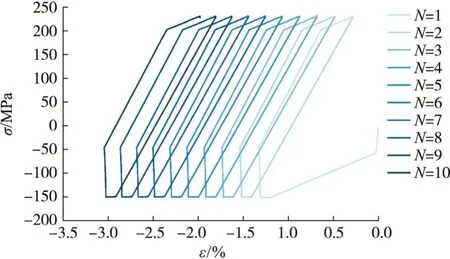
圖8 G點10次循環應力-應變響應Fig.8 Stress-strain response of point G in 10 cycles

圖9 F、G點10次循環殘余應變的變化Fig.9 Residual strain evolution at F and G in 10 cycles

2.4 結構疲勞失效分析

由于單次循環結構承受的最大應力小于材料斷裂破壞的臨界應力,結構中的斷裂序參量增長較小。循環加載并計算結構的斷裂序參量,直至結構中出現序參量值達到0.95則停止計算。最終發現,91個循環后結構失效,計算停止,F點斷裂序參量最先達到臨界值c=0.95,表明結構的疲勞壽命為91次循環,失效點位于內壁下表面F點。

單次循環后的序參量分布如圖10所示。圖10表明,結構中內壁下表面中心點F序參量最大,在單次工作結束后,F點的損傷最大,但此時序參量的值還處于很低的水平,對結構的承載能力影響不大,不會使應力衰減,仍可以進行多次循環工作。結構在內壁下表面受到的溫度載荷最高,并且F點由于對稱邊界受到約束,在溫度恢復常溫后,受到的拉應力最大,所以序參量演化最快。根據應力分布云圖,在結構變截面處,即C、D點會出現應力集中。C點受到的溫度載荷較低,所以溫度載荷恢復后受到的載荷水平較低,沒有出現損傷。D點受到的溫度載荷較高,相場值為6×10-7,但與F點相比仍較低,因此結構并未在變截面處出現裂紋。

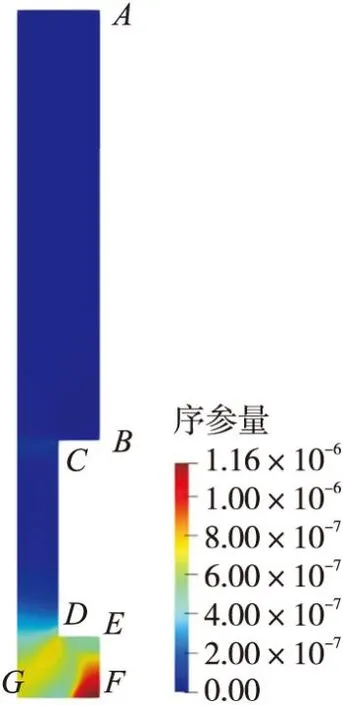
圖10 單次工作后相場序參量分布Fig.10 Distribution of phase-field order parameter after 1 cycle

10次循環后的序參量分布如圖11所示,結果與單次循環相似,仍在F點序參量值最高。

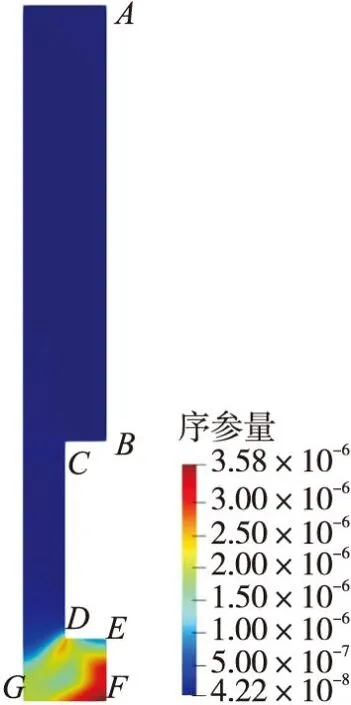
圖11 10次工作后相場序參量分布Fig.11 Distribution of phase-field order parameter after 10 cycles

結構中的斷裂序參量演化如圖12所示。隨著循環數增加,下表面的斷裂序參量值不斷上升,并且EF邊界明顯快于內壁其他區域,從F點到E點從大到小基本呈線性分布。

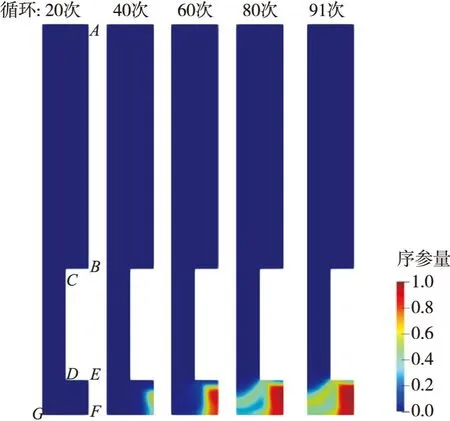
圖12 相場序參量演化Fig.12 Evolution of phase-field order parameter

結構失效破壞時的徑向位移如圖13所示。疲勞破壞時,EF邊界明顯向下凹陷,內壁不斷變薄,最終在F點處斷裂失效。

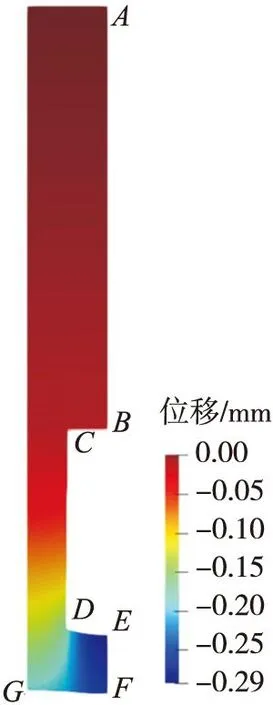
圖13 結構破壞時的徑向位移Fig.13 Radial displacement at failure

3 結論

本文采用熱-彈-塑性耦合的疲勞斷裂相場模型,分析了火箭發動機再生冷卻推力室結構在循環運行過程中的溫度、應力和應變分布及變化,根據斷裂序參量的演化,分析了熱機疲勞破壞行為并計算了結構的疲勞壽命,主要結論如下。

1)推力室結構在工作過程中熱量自下而上傳導,溫度逐漸降低。結構升溫降溫產生的塑性變形是導致結構疲勞失效的主要因素。

2)結構內壁部分變形較大,隨著循環次數增加,F點和G點分別不斷累積殘余正應變和殘余壓應變。

3)F點受到殘余正應變積累,驅動裂紋擴張的拉伸應變能不斷增加,最終導致結構發生疲勞破壞。內壁中心受到殘余正應變,使內壁向下表面塌陷,壁面變薄。