空間多目標掠飛觀測接近軌道設計方法 *

劉育昊，張兵，方子今

（1. 航天科工空間工程發展有限公司，北京 100854；2. 航天科工第二研究院 研究生院，北京 100854）

0 引言

隨著空間目標的日益增多以及空間環境的日漸復雜，各國對于空間態勢感知能力的要求越來越高，而空間目標天基觀測系統是未來空間態勢感知的重要發展方向［1］。前人在天基空間目標觀測領域也做了很多的研究。文獻［2］研究了對于一個確定目標找到一條燃料最優轉移軌道采用機動變軌方式進行觀測的問題，該方法存在觀測效率低，付出代價大的缺點。文獻［3］研究了采用不變軌的方式對多個目標進行抵近，問題在于它采用雙星基準確定初軌的方式，該定軌方式對于前2 個目標的觀測屬于一個軌道周期內完成觀測，并不滿足全局最優，且該方式對于目標的位置與時間要求較高。此外，它簡單地滿足了距離約束，并未考慮天光地影條件以及相對角速度約束對于觀測效果的影響。

為了獲得更好的觀測效果，在滿足天光地影約束條件以及相對角速度約束條件下，觀測距離越近越好。在一次空間觀測任務中，航天器所帶燃料十分有限，而最為節省燃料的方式就是航天器在自身軌道上自然飛行的同時實現對目標的觀測［4-9］。

本文重點研究了在滿足天光地影約束條件和相對角速度約束條件下，從優化軌道六根數的角度出發，對多目標進行近距離掠飛觀測的軌道設計方法，解決了在空間天基領域觀測效率低、效果不好的問題。

1 空間多目標觀測模型

1.1 求解兩軌道面目標的最近距離

1.1.1 理論最近距離求解

如圖1 所示，假設航天器A和目標衛星T1的軌道均為近圓軌道。航天器A的軌道面P與目標衛星T1軌道面P1存在交線L1，理論上當航天器A與目標衛星T1同時運行到交線的同一端的時候，它們之間的距離將達到最小值，此時的最小值只是理論上的最小值，航天器和衛星要經過長時間的在軌運行，利用軌道高度差產生的周期差，才可能使它們同時到達交線位置。然而從實際情況來說，通常是不能同時運行到交線上的，總是會差一些相位，即得不到這個理論最小值，所以我們需要計算在一定的時長內，航天器與目標所能達到的最近距離［3］。

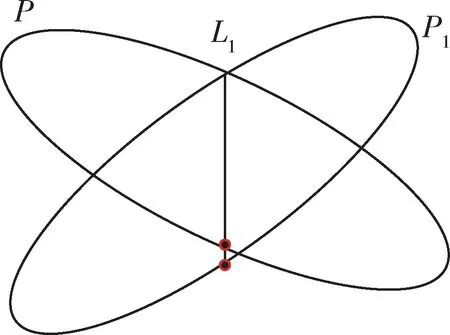
圖1 兩軌道面日標最近距離示意圖Fig. 1 Schematic diagram of the nearest distancebetween targets on two orbit planes

根據以上分析可知，航天器與目標之間的最近距離在它們軌道面交線得到，由此可以得到一個一定時長內航天器與目標最近距離的求解方案：在一定時長內，求出航天器位于軌道面交線上的各個時刻以及這些時刻目標在軌道上所對應的位置，然后求出這些位置點與地心連線與交線夾角的角度，最小角度所對應目標點的位置即為這段時間內航天器與目標最近距離所對應的位置，公式推導如下。

由軌道根數可得軌道面的法向矢量為

假設航天器軌道面與目標衛星軌道面的法向矢量分別為n1和n2，由此可以得到兩軌道面的交線矢量為

偏心率單位矢量為

當航天器與目標衛星同時到達交線位置時，由交線矢量RC及偏心率單位矢量e可求得航天器與目標衛星的真近點角f1和f2分別為

假定航天器與目標衛星在各自軌道上真近點角分別為f1和f2處的地心矢量分別為R1和R2，此時航天器與目標衛星理論上的最近距離為

因為2 個軌道面有2 個交點，將f1和f2加上180°后，依舊利用式（5）即可求得航天器與目標衛星在交線另一端的最近距離理論值Rmin，由此即可得到航天器與目標衛星的理論最近距離。

1.1.2 實際最近距離求解

以上計算的是航天器與目標衛星理論上的最小距離，而在實際運行當中幾乎不可能達到理論上最小值所對應的位置。接下來是對限定時間內，航天器與目標衛星實際所能達到最近距離的求解。

將航天器在交線處的真近點角轉化成偏近點角：

將偏近點角再轉化為平近點角：

航天器在軌道上的平動速度為

式中：μ為地心引力常數；a1為航天器軌道半長軸；e1為偏心率矢量e1的大小。

由此可以得到航天器通過交線位置的時刻為

式中：tp1為航天器通過近地點的時刻。

在t1基礎上加上航天器周期的整數倍即可得到航天器每次通過交線處的時刻為t1i(i=0，1，2，…，Imax)，其中，Imax為限定時間內，航天器在軌道上運行的最大圈數。通過所求得的t1i可以求得目標衛星在對應時刻的平近點角，進而可得到對應的真近點角f2i。

接下來計算在一定的時間內，每次航天器運行到交線位置上時，目標衛星與交線位置處的真近點角之差，并找出這個差值的最小值fmin以及當差值最小時所對應的時刻tmin為

此時，找出fmin所對應的真近點角，得出目標衛星在它軌道上真近點角為處的地心矢量，進而得到航天器與目標衛星實際上的最近距離為

1.2 天光地影光照條件

為了獲得對空間目標的良好觀測效果，除了要滿足適宜的距離約束以外，良好的光照條件也是必不可少的條件。首先，目標不能處于地球的陰影之中，即要滿足地影光照條件約束；其次，觀測航天器要在目標的順光位置進行觀測［10］。

1.2.1 地影光照條件約束

光學觀測要求目標是被照亮的，不能被地球遮擋住太陽的光線。設地心慣性坐標系中，目標的位置矢量為rT，太陽位置矢量為rsun，RE是地球半徑。令

則

依如下判斷方法判斷空間目標是否處于地影之中：當D＞0 時：空間目標在地影之外，滿足地影觀測條件。當D≤0 時：當≥H2時，目標衛星在地影之外，滿足觀測條件；當＜H2時，目標衛星在地影之內，不滿足觀測條件。

地影光照條件示意圖如圖2 所示。

圖2 地影光照條件示意圖Fig. 2 Schematic diagram of ground shadow illumination conditions

1.2.2 天光光照條件約束

為了保證航天器對目標良好的觀測效果，除了目標要處于地影之外，觀測器與目標衛星的相對位置也很重要，即觀測器要處于順光位上進行觀測。此時觀測器-目標衛星-太陽之間的相角αsun小于某個門限值（＜90°）。如果相角太大，則說明此時觀測衛星是在背光的位置對目標進行觀測，此時目標觀測面沒有光線反射，顯得比較暗，觀測困難，對于設備的識別能力以及觀測精度都有很大的影響，沒有辦法保證良好的觀測效果。

根據上述所說，給出一個合理的可觀測時刻觀測器-目標衛星-太陽的太陽相角值是十分必要的。太陽角光照條件約束的示意圖如圖3所示。

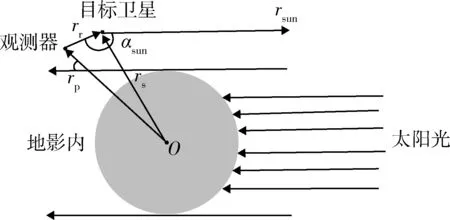
圖3 太陽角光照條件示意圖Fig. 3 schematic diagram of solar angle illumination conditions

已知地心慣性系中衛星到目標的矢量為

因此，太陽相角αsun可由式（17）求得：

1.3 坐標系轉換

在進行1.2 里光照條件的判定時，要計算特定時刻的太陽矢量rsun。首先計算出的太陽矢量rsun是在慣性坐標系中的，而進行天光地影光照條件判斷的時候，需要將rsun轉移到軌道坐標系中。

如圖4 所示，地心慣性坐標系Oxyz定義為：原點O位于地球中心，x軸指向春分點，z軸指向地球的北極，y軸與x軸和z軸組成右手坐標系。軌道坐標系(O0x0y0z0)定義為O0原點位于衛星質心，z0軸與衛星的矢徑共線并指向地心，x0軸位于軌道平面內，與衛星運動方向相同，y0軸同理與x0軸和z0軸組成右手坐標系［11］。

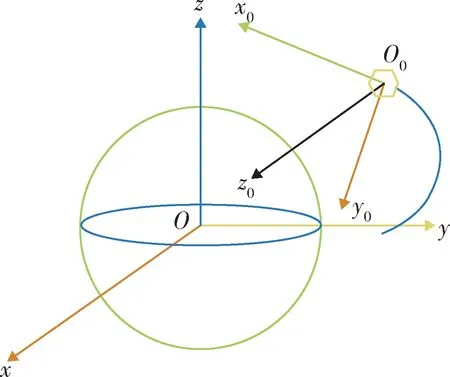
圖4 慣性坐標系和軌道坐標系Fig. 4 Inertial and orbital coordinate systems

本文采用間接轉換法進行坐標轉換，根據衛星軌道根數計算慣性坐標系到軌道坐標系的姿態轉換矩陣，從而實現坐標系的轉換。該方法的數學表達式如下：

式中：Lx，Lz分別為繞x，z軸旋轉的旋轉矩陣；u，i和Ω分別為衛星開普勒軌道參數中的緯度幅角、軌道傾角和升交點赤經；L001為坐標軸的反向矩陣，且

1.4 瞬時相對角速度計算

在進行天基觀測的時候，觀測器與目標衛星在滿足了良好光照條件和距離約束的情況下，還需滿足相對角速度的約束才能實現良好的觀測效果。如果相對角速度過大，超過了某一最大限定值wmax，觀測器對于目標衛星將來不及進行調姿觀測，同樣無法獲得良好的觀測效果。因此，為了保證良好的觀測效果，對于觀測器與目標衛星相對角速度的約束也是十分必要的。

如圖5 所示，假設觀測器在某時刻t相對于地心的位置矢量為r1，目標衛星相對于地心的位置矢量為r2，二者的相對位置矢量為rT1=r2-r1。經過一個極短時間Δt后，在t+ Δt時刻，觀測器相對于地心的位置矢量為，目標衛星相對于地心的位置矢量為，二者的相對位置矢量為=。此時視線角變化為

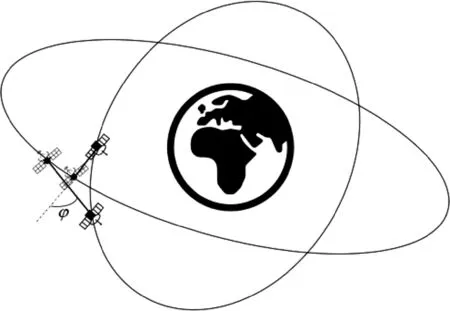
圖5 相對角速度計算示意圖Fig. 5 Schematic diagram of relative angular velocity calculation

此時可計算出瞬時相對角速度為

當w≤wmax時，可視為觀測器在時刻t對目標衛星的觀測符合相對角速度約束。

2 粒子群優化算法

為了找到對于多個目標觀測距離最小的軌道，就要對觀測器軌道的初始狀態進行優化，即對觀測器軌道的初始六根數進行優化從而確定初始軌道以實現觀測器對多個目標衛星的觀測。粒子群算法（partical swarm optimization，PSO）是用于解決優化問題的典型算法。基本思想是通過群體中個體之間的協作和信息共享來尋找最優解［12-13］。

在PSO 中，每個優化問題的潛在解都是搜索空間中的一只鳥，抽象為粒子，每個粒子都有一個由目標函數決定的適應值，以及決定它們飛行的方向和距離。PSO 具有實現容易、精度高、收斂快等優點。

2.1 確立目標函數

有m個目標分別在各自的軌道上運行，觀測器也在自己的軌道上運行。觀測器有自己的最大觀測距離Rmax，在一定的時間內，觀測器有機會接近目標。當觀測器與目標的距離在Rmax之內，且滿足1.2中的天光地影條件和1.4 中的相對角速度約束時，即可視為觀測成功，而當觀測距離越近的時候可視為觀測效果最好。設對第1 個目標的觀測距離為R1，對第m個目標的觀測距離為Rm，目標函數設為

當以上目標函數取得最小值的時候，即可認為實現了對該m個目標的最佳觀測。

2.2 算法流程

粒子群算法由隨機解出發，通過迭代來尋找最優解。每個粒子在搜索空間中單獨搜尋最優解，并將其記為當前個體極值與整個粒子群里的其他粒子共享，找到最優的個體極值作為整個粒子群當前的全局最優解，粒子群中所有粒子根據自己當前的個體極值與當前的全局最優解來調整自己的位置和速度。

首先，要設置粒子的最大速度區間，防止超出最大的空間。位置信息即為整個搜索空間，即為觀測器軌道六根數的范圍。在任務開始時刻的軌道高度范圍設置為目標軌道高度上下最大觀測距離的范圍內。因目標衛星軌道為近圓軌道，觀測器軌道也應為近圓軌道，所以偏心率設置為一個接近于0 的極小數即可。軌道傾角的搜索范圍設置為0°～90°。升交點赤經的搜索范圍為0°～360°。因軌道為近圓軌道，近地點幅角的意義不是很大，因此設定為0°～360°之內的任意數即可。以上5 個根數可將觀測器的軌道確立下來，真近點角的意義是觀測器在任務開始時在軌道上的位置，搜索范圍也為0°～360°即可。由此可將搜索空間確立下來。在速度區間與搜索空間上隨機初始化粒子的速度與位置，設置群體規模為m。

個體極值為每個粒子找到的歷史上最優的位置，并從這些個體歷史最優解中找到一個全局最優解，并與歷史最優解比較，選出最優解作為當前歷史最優解［14-16］。

速度與位置的更新公式如下：

式中：w為慣性因子；Ci為加速常數；x1和x2為[0，1]上的隨機數；Pid為第i個變量的個體最優解；Pgd表為當前全局最優解；Xid為個體最優解對應的粒子的位置。

當達到最大迭代次Gmax時，停止尋優。算法流程圖如圖6 所示。

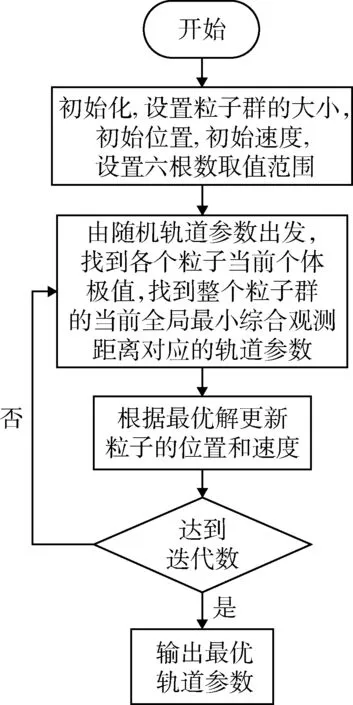
圖6 粒子群算法流程圖Fig. 6 Flow chart of particle swarm optimization

3 仿真校驗

3.1 仿真條件

任務背景是有3 顆低軌衛星在軌飛行，觀測器本身在自身軌道上飛行，目標衛星在2022-01-01 T 00：00：00 的軌道參數如表1 所示。觀測器的最大觀測距離為30 km，最大的觀測太陽角為90°，最大相對角速度為10 （°）/s。任務時長為2 個月，要設計一個觀測器的觀測軌道，使得觀測器在軌飛行2 個月的時間里對于3 個目標的綜合觀測距離最小。太陽矢量的計算以2021-01-01 T 00：00：00 的太陽矢量參數為基準進行遞推計算。

表1 目標軌道根數Table 1 Orbit parameters of the target

3.2 仿真結果與分析

設置好粒子群算法參數，慣性因子w設置為0.9，加速常數C1和C2設置為0.5，種群大小設置為50，迭代次數設置為25，在觀測器六根數的可取范圍內進行尋優。

目標函數為3 顆衛星觀測距離的均方根，目標函數隨迭代數的變化如圖7 所示。

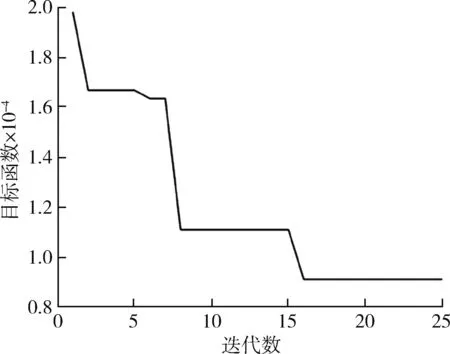
圖7 綜合距離迭代圖Fig. 7 Iterative graph of comprehensive distance

最終優化出的最優觀測距離為9.127 5 km，優化出的最優結果所對應的觀測器在2022-01-01 T 00：00：00 所對應的軌道根數如表2 所示。

表2 觀測器軌道根數Table 2 Orbit alparameters of the observer

達到對3 個目標綜合觀測距離最小的情況下，對各個目標的具體觀測數據如表3 所示。

表3 對各個目標的觀測數據Table 3 Observation data of each target

在綜合最優觀測距離情況下，目標與觀測器的軌道位置如圖7 所示。

由圖7 綜合距離變化圖可以看出，結果收斂效果良好，最終的綜合距離優化結果在10 km 以內，能夠在完全不變軌的情況下實現對3 個目標的較近距離觀測，且完全滿足天光地影觀測條件，能夠獲得較為良好的觀測效果。由圖8 目標與觀測器的軌道位置圖可知，對目標的近距離觀測只能在兩軌道的“十字路口”附近實現，符合實際。

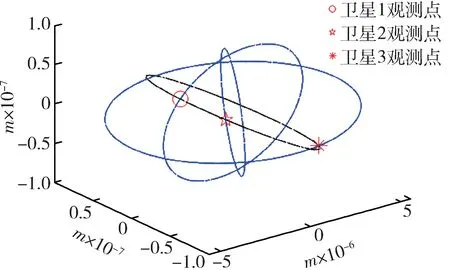
圖8 目標與觀測器軌道位置圖Fig. 8 Orbit diagram of target and observer

由表2 可以得到，最優的觀測器軌道高度會比目標的軌道高度偏移一定的距離，這個距離不能太小也不能太大，太小將會導致觀測器軌道周期與目標軌道的周期差太小，不容易通過周期差來消除相位之間的差距，太大將會導致觀測器對于目標軌道的可視范圍變小從而觀測成功的機率變小且觀測距離變大而導致觀測效果的降低。目標的軌道傾角都比較大，所以在極地附近，目標會稍顯密集，當觀測器軌道傾角比較大的時候，“十字路口”會出現極地附近，更容易觀測到目標。

4 結束語

針對空間目標的觀測效率低，觀測效果不好，燃料不夠等問題，本文基于粒子群算法對觀測器軌道的六根數進行優化，提出一種多目標掠飛觀測接近軌道的設計方法，利用觀測器軌道與目標軌道高度之差而產生的周期之差抵消交線處相位與目標相位之差，以實現以消耗時間為代價，在不變軌消耗燃料的情況下實現對多個空間目標的近距離觀測。最后利用Matlab 仿真來驗證方法的合理性。本文對空間目標觀測的研究可以為我國未來空間觀測領域研究提供一定的理論基礎。