新能源并網點阻抗比對臨界短路比的影響分析

李勝男，何鑫，張丹，鄧燦

（1.云南電網有限責任公司電力科學研究院，云南 昆明 650217；2.云南電力調度控制中心，云南 昆明 650011）

0 前言

近年來我國隨著新型電力系統的建設，新能源發電占總發電量的比例日益增高。根據國家能源局的統計數據，2023年底我國以風電和光伏為代表的新能源裝機容量已突破10億千瓦。當前，大規模新能源發電、柔性直流輸電等電力電子設備接入系統存在規模受限、暫態過電壓、控制失穩等問題，其嚴重程度與系統的電壓支撐強度密切相關。短路比(Short Circuit Ratio, SCR)是目前最常用的系統電壓支撐強度衡量指標[1]，可衡量換流器接入規模與交流側短路容量的相對大小，能夠簡單直觀地反映系統的相對強弱。臨界短路比(Critical Short Circuit Ratio, CSCR)為系統臨界穩定時的SCR，表示系統SCR穩定運行時的下限值[1]，SCR與CSCR的差值越大，代表系統的電壓穩定裕度越大。文獻[2]提出新能源和直流并網系統的電壓支撐強度，分別取2和3作為系統強弱的分界值。文獻[3]使用臨界值為2的改進多饋入有效短路比來衡量含靜止同步補償器系統的電壓支撐強度。目前，國家強制性標準GB38755-2019《電力系統安全穩定導則》明確要求新能源場站短路比應達到合理水平[4-6]，文獻[7-8]利用電壓靈敏度方法，求得新能源CSCR的值為。文獻[9]通過新能源多場站接入系統模型推導和仿真，得到多場站臨界短路比的穩定性指標為2.0~2.5。文獻[10-11]定義了場站相關短路比臨界值為1。但無論是哪種CSCR的定義方法，其臨界狀態均為靜態電壓穩定極限，當傳輸功率小于P-V曲線“鼻尖點”處傳輸功率極限即可說明系統電壓支撐強度良好。因此文獻[12]提出當SCR大于2時系統較強，反之則系統較弱，這是由不同傳輸功率下取得的CSCR最大值再額外保留一定裕度得到的。但現有研究中各種方法構建的新能源并網CSCR基本都是綜合表征，忽略了實際并網點等值阻抗角度的影響。首先，多新能源場站接入系統實際運行中，新能源場站需要提供無功功率用以補償新能源場站內集電線、站外送出線路的部分無功損耗[7]；其次，云南風光資源分散，大量新能源需通過110 kV線路或35 kV外送，線路電阻分量較大，當一個片區多個新能源場站集中并網上送時，各場站并網點母線節點間阻抗角及初始相位角均可能存在較大差異。忽略了系統等值阻抗電阻部分影響及各場站之間電壓相角相同的假設，無法反映新能源發電設備的無功輸出、新能源場站內不同節點之間各電氣量幅值、相位差的區別。

為此，本文在短路比和阻抗比計算的基礎上，以一個簡單的算例演示了阻抗比對穩定的影響，直觀地給出了這種簡單系統的定量分析結果，推導給出阻抗比與最大傳輸功率的關系、與交流系統參數的關系，最后給出臨界短路比和阻抗比的關系，量化阻抗比對臨界短路比的影響。

1 短路比與阻抗比計算

1.1 短路比和阻抗比的定義

短路比目前是衡量交直流系統電壓支撐強度的有效指標，電力系統網絡某點的短路容量等于該點三相短路電流與額定電壓的乘積，是系統強度的標志。電力電子設備接入后的電壓支撐強度可以通過交流系統短路容量與設備額定容量的比值大小，即短路比（short circuit ratio，SCR）進行衡量：

式中：Sac為交流系統短路容量，單位為MVA；PN為該節點的設備容量，單位為MW。式中，PN可以看做這個節點的最大功率。

在開路電壓（即等值內電勢）為1.0 p.u.的前提下，短路比可以表示為

進而，若選取標幺基準功率為換流器額定功率PN，即PN為1.0 p.u.，短路比可以寫為：

由上式可知，短路比在一定基值選取的前提下，是一個只由系統等值阻抗的模值表示的參數。但由實際系統的方程可知，一個交直流系統的穩定性不僅僅與戴維南等值阻抗的模值有關，與阻抗相角也息息相關。評估電壓支撐強度時主要考慮阻抗幅值的影響，針對大規模新能源并網系統送、受端距離較遠或新能源接入低電壓等級電網的情形，電阻影響較大，電壓支撐強度的量化評估需綜合考慮阻抗幅值與相角的影響。為此需要引入阻抗比的定義：

阻抗比（impedance ratio, IR）為交流系統戴維南等值電抗與戴維南等值電阻之間的比值，描述了系統阻抗角。阻抗比指標以及其與阻抗角之間的關系為：

式中：X為系統戴維南等值電抗；R為戴維南等值電組；φ為系統戴維南等值阻抗角。高壓系統中，元件電阻通常小于其電抗，分析時可忽略電阻的影響。但是新能源通常經35 kV或110 kV線路接入系統，此時電阻相對電抗已經不可忽略，部分35 kV電壓等級的線路電阻甚至大于電抗，阻抗比較小，忽略電阻將增大分析誤差。

1.2 阻抗比對穩定影響的簡單算例推導

為了說明這個情況，這里采用一個很簡單的算例。例如圖1所示的系統：

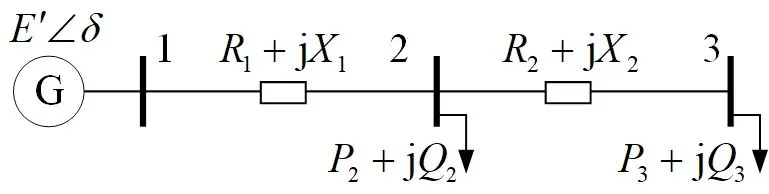
圖1 簡單電力輸電網絡

假設在該算例中，發電機采用經典模型，負荷采用恒阻抗模型。潮流計算中，節點1設定為電壓相位參考節點，發電機內節點電勢保持恒定。它所采用的方程描述如下：

對同步發電機：

網絡方程這里不消去任何節點，最直觀的表示如下：

發電機方程：

負荷方程：

算例說明：

首先，本算例中只有一個同步發電機，故本算例不用于同步穩定性問題的分析，同步穩定性問題分析中需要至少包含2個同步發電機，才能夠出現功角問題。其次，在后面的分析中，設定Pm是常數，意味著原動機的出力也是恒定的，故不考慮調頻問題。本算例既然不關系同步穩定性和頻率穩定性，那就只關系到潮流和電壓問題。

在圖1所示線路的阻抗的模值不變的基礎上，適當提高線路的阻抗比，將線路阻抗比X/R=2提高到X/R=4。此時可計算得R1+jX1=0.0016+j0.0065。重復計算該算例，得到如表1所示的結果。

表1 線路阻抗比增加后的潮流

表1與表2對比，在線路阻抗比增加后，節點2、3的節點電壓有所增加，而節點相角差也有所增加。

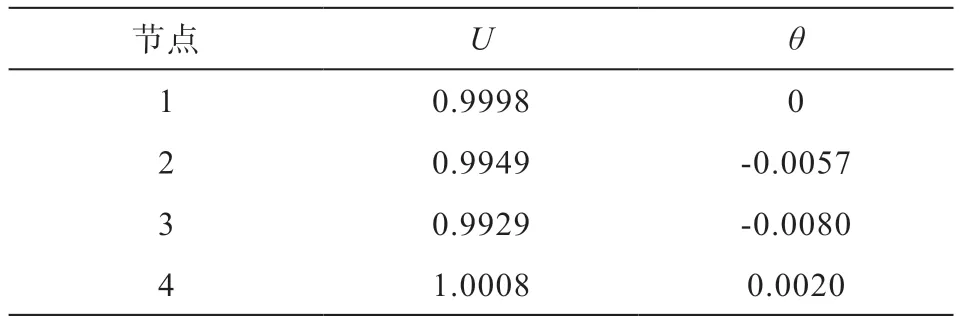
表2 阻抗比增加后節點2負荷增加0.5倍的潮流

表3 阻抗比增加后節點3負荷增加0.5倍的潮流

(1)對節點2的負荷增加0.5倍，即取P2+jQ2=(0.4+j0.2)*1.5，其他數據不變，潮流結果如下：

(2)對節點3的負荷增加0.5倍，即取P3+jQ3=(0.4+j0.2)*1.5，其他數據不變，潮流結果如下：

在此算例中的給定數據條件下，節點電壓增加（即節點間電壓差減小），而節點相角增加。但在改變負荷取值時，又會得到不同的結果。

經過理論推導發現，阻抗比和潮流結果并非是單一線性的關系，阻抗比對潮流結果的影響，還取決于負荷值PL+jQL、線路阻抗的模值|Z|和發電機暫態電動勢E'。在不同的取值下，線路阻抗比變化對潮流結果的影響不是單調的。但仍都會導致節點電壓和相角發生改變，從而使系統穩定性發生改變。

由此可見網架結構相同，但是阻抗參數的變化導致穩定性結果是不同的。為此開展阻抗比研究。

2 阻抗比與交流系統功率和參數的關系

2.1 阻抗比對最大傳輸功率的影響

電力網絡之間能夠傳輸的最大有功功率是衡量系統電壓穩定性的方法之一，一般來說，能夠傳輸的有功功率越大，說明了系統的電壓穩定性越強。因此，研究阻抗比對交直流系統之間最大功率傳輸，可以研究阻抗比對交直流系統電壓支撐強度的影響。

這里采用如圖2所示的簡化系統進行分析：

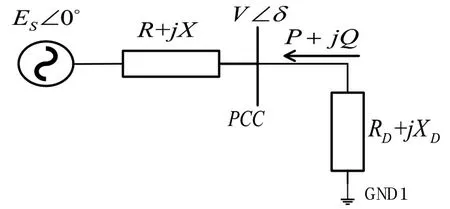
圖2 簡化交直流系統

圖中Es∠0°為戴維南等效電動勢；R+jX為戴維南等效阻抗，也可以寫成|ZN|∠φ；V∠δ為交直流連接母線電壓；P+jQ為交直流之間傳輸的功率，當換流器為逆變器時，功率流向如圖中所示，當換流器為整流器時，功率流向與圖中相反；RD+jXD為直流系統等值阻抗。

我們先考慮當換流器為新能源發電設備逆變器的情況，即有功P是流向交流系統的，則對PCC點列功率方程有：

即：

將R+jX寫成|ZN|∠θ，則上式可改寫為：

由cos2(φ+δ)+sin2(φ+δ)=1聯立實部虛部方程，得到關于并網點電壓平方的一元二次方程：

對上式求解，得到并網點電壓方程為：

式中：?為一元二次方程判別式；λ、μ為計算因子，λ=(PR+QX)/E2，μ=(PX-QR)/E2。

當?=0時，并網點電壓有唯一物理解，對應于系統臨界穩定狀態。此時，最大傳輸功率Pmax及并網點臨界電壓Ucri分別為：

不妨取k=X/R，由知，

代入整理有：

由式（19）可得，?Pmax/?k的正負與無功Q的取值有關，當Q＞0時，顯然有?Pmax/?k＜0，即最大傳輸有功隨阻抗比的增大而減小；當Q＜0時，?Pmax/?k取決于Q與E的取值，因此不方便判斷正負；但在實際新能源接入系統中，對新能源接入的電壓控制，使得我們往往認為只輸出有功功率P，即Q=0。在此前提下，對上式重新推導，得到：

研究式的單調性，求解得到?Pmax/?k＜0，即最大傳輸有功隨阻抗比的增大而減小，與Q＞0時結論一致。

2.2 交流系統參數對阻抗比的影響

阻抗比作為一個穩態下的交流系統等效參數，求解過程可以按照穩態運行下的戴維南等值推導。具體的影響阻抗比的參數有很多，但尋找一個對阻抗比影響最大的參數，對于調節阻抗比，進而得到一個系統更為優秀的電壓支撐強度，提高電壓穩定性，具有重要工程意義。

這個問題本質上就是求解阻抗比對系統參數p的靈敏度d(X/R)/dp。事實上：

所以問題可以轉化為求解系統的戴維南等值阻抗及求戴維南等值阻抗對系統參數的靈敏度?(ZN)/?p。

假設換流器并聯母線為節點i，ZN可以系統穩態情況下的戴維南等值電路表達，如圖3所示。

圖3 戴維南等值電路圖

圖4 CSCR對IR的導數

圖5 阻抗比對臨界短路比的影響

ZN=eiT-1ei，其中表示節點等值導納矩陣，ei表示第i個標準規格化的單位列向量，即單位矩陣的第i列。

又=I,則有：

將代入式中去，可以得到：

在式（24）的求解過程中，有對矩陣求逆的過程，在大系統中，這勢必會影響計算速度，這里采取LU分解和前推回代法，對式（24）的等式右邊按照從右往左的順序依次求解，可以大大減少計算量。

進而有：

進而將式（25）代入式（24）和式（21）中，可以計算得交流系統阻抗比對節點j負荷變化的靈敏度。

3 阻抗比與新能源并網臨界短路比的關系

系統臨界穩定時對應的短路比為臨界短路比，因短路比指標構建方法多樣，臨界短路比存在計算不統一的問題。系統靜態電壓失穩源于潮流超過系統最大傳輸功率，各種靜態電壓指標本質上以達到最大傳輸功率作為電壓崩潰的臨界點，臨界短路比的計算與最大傳輸功率密切相關。由上一節推導，最大傳輸功率與阻抗比有關，因此可以構建臨界短路比與阻抗比的關系。

我們這里提出另一種簡化臨界短路比求法：由式（2）知，短路比為關于PN的單調減函數。當在系統無功水平一定的情況下（新能源接入系統時一般認為是0），結合最大傳輸功率Pmax，在開路電壓為1.0 p.u.的前提下，根據短路比的定義可以求取該系統的臨界短路比為：

不妨令E、均取為1，將式（20）代入式（27），得到：

由2.1節討論得知，在新能源接入系統中，最大傳輸功率Pmax隨阻抗比的增大而減小，因此對于基于最大傳輸功率求得的臨界短路比，阻抗比越大，臨界短路比就越大，即電壓支撐強度隨著CSCR與IR關系阻抗比增大而減弱。

先增大后降低，事實上，當IR＞5時，其對臨界短路比的導數已經小于0.1，說明當阻抗比大于5時，阻抗比對臨界短路比的影響較小，即阻抗比對電壓支撐強度影響較小，此時采用短路比衡量電壓支撐強度可以忽略阻抗比的影響。

4 結束語

本文介紹了衡量新能源接入系統電壓支撐強度的輔助指標——阻抗比的定義和推演，所得結論如下：

1）與短路比類似，阻抗比對系統電壓支撐強度的影響也可以用最大傳輸功率來衡量，在新能源接入的情況下，阻抗比越大，最大傳輸功率越小，但在交直流連接的研究中，阻抗比和最大傳輸功率沒有明確的單調性關系，需根據實際情況的其他參數取值具體分析。

2）根據阻抗比與最大傳輸功率的關系，推導了阻抗比對系統參數靈敏度的求解方法，進一步得到阻抗比與臨界短路比的關系，闡明了阻抗比與短路比之間的聯系。最后，對實際系統中如何合理高效地應用阻抗比指標作為臨界短路比補充判據提供了借鑒。