城市軌道交通線路建設(shè)時(shí)序研究

葛馨茹

摘 要：為合理決策軌道交通建設(shè)時(shí)序，將城市軌道交通線路建設(shè)時(shí)序的確定視為多因素決策問題，提出基于Pythagorean模糊熵的優(yōu)劣解距離法。將傳統(tǒng)的一次性靜態(tài)建設(shè)時(shí)序確定過程轉(zhuǎn)化為多次動(dòng)態(tài)決策，綜合考慮決策者在不同時(shí)段對(duì)決定線路建設(shè)時(shí)序的各影響因素重視程度不同，為影響因素指標(biāo)賦權(quán)，計(jì)算各時(shí)段未確定建設(shè)時(shí)序的線路與理想解的綜合貼近度，進(jìn)而確定線路建設(shè)時(shí)序。應(yīng)用所提出的決策方法確定重慶市城市軌道交通第四期規(guī)劃線路建設(shè)時(shí)序，與實(shí)際規(guī)劃時(shí)序基本一致。

關(guān)鍵詞：城市軌道交通 線路動(dòng)態(tài)建設(shè)時(shí)序 Pythagorean模糊熵 TOPSIS模型

城市軌道交通建設(shè)具有周期性長(zhǎng)、成本較高、建成后調(diào)整難度大等特性，合理且具有前瞻性的線網(wǎng)規(guī)劃至關(guān)重要。目前，國(guó)內(nèi)外學(xué)者對(duì)于城市軌道交通項(xiàng)目建設(shè)時(shí)序確定的研究相對(duì)較少。概括來講，已有的研究思路主要?dú)w為兩類，一類是引入某種思想或是基于某種決策方法，量化各線路的重要程度，進(jìn)而對(duì)其建設(shè)優(yōu)先級(jí)加以排序；另一類是從線網(wǎng)整體角度分析，構(gòu)建成本—效益模型，計(jì)算不同建設(shè)順序所對(duì)應(yīng)的成本與效益，選擇綜合效益最大的建設(shè)方案。文獻(xiàn)[1]引入格序決策理論，依據(jù)灰色關(guān)聯(lián)分析法，比較各條線路與理想方案的綜合偏差大小，確定建設(shè)時(shí)序。文獻(xiàn)[2]對(duì)線路各站點(diǎn)建立節(jié)點(diǎn)重要性指標(biāo)，量化加權(quán)累加得到各線路重要度，依據(jù)評(píng)價(jià)結(jié)果確定建設(shè)時(shí)序。文獻(xiàn)[3]基于累計(jì)前景理論，構(gòu)建成本-效益最大化優(yōu)化模型，計(jì)算不同建設(shè)時(shí)序的線網(wǎng)建設(shè)方案的綜合前景值，確定最優(yōu)建設(shè)時(shí)序方案。盡管現(xiàn)有研究成果可以一定程度上幫助軌道交通建設(shè)時(shí)序決策者有效度量線網(wǎng)中各線路的相對(duì)重要性，但多關(guān)注靜態(tài)層面，確定建設(shè)時(shí)序時(shí)沒有考慮線路逐漸網(wǎng)絡(luò)化的動(dòng)態(tài)過程，忽視優(yōu)先建設(shè)線路對(duì)其余規(guī)劃線路的影響。

因此，本文將傳統(tǒng)的一次性靜態(tài)建設(shè)時(shí)序確定過程動(dòng)態(tài)化，將其轉(zhuǎn)化為多次動(dòng)態(tài)決策，且考慮不同建設(shè)時(shí)段決策者對(duì)各影響因素重視程度的差異，對(duì)規(guī)劃線路的建設(shè)時(shí)序進(jìn)行綜合確定，使決策結(jié)果更貼近工程實(shí)際。

1 建設(shè)時(shí)序影響因素指標(biāo)體系構(gòu)建

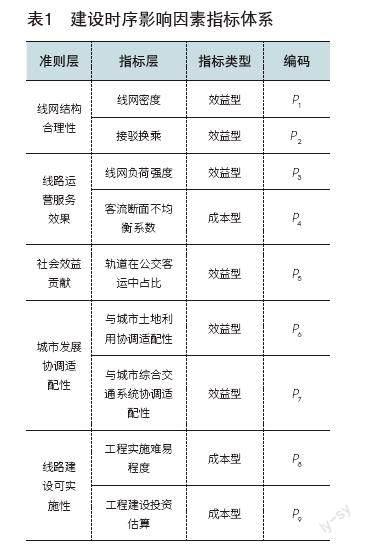
合理的構(gòu)建線路建設(shè)時(shí)序影響因素指標(biāo)體系是科學(xué)確定建設(shè)方案的前提，對(duì)影響因素的選取既要全面分析，又不應(yīng)繁復(fù)冗雜。本文重點(diǎn)梳理提煉文獻(xiàn)[4-6]中的共性指標(biāo)，并結(jié)合上海、北京、西安、柳州等城市軌道交通線網(wǎng)規(guī)劃綜合評(píng)價(jià)中所采用的指標(biāo)體系，從線路的結(jié)構(gòu)性、線路運(yùn)營(yíng)后對(duì)居民出行需求的滿足性、線路建設(shè)的可實(shí)施性、線路建設(shè)對(duì)社會(huì)效益的貢獻(xiàn)情況以及線路建設(shè)與城市發(fā)展的協(xié)調(diào)適配性等角度，構(gòu)建線路建設(shè)時(shí)序影響因素指標(biāo)體系，具體各級(jí)評(píng)價(jià)指標(biāo)如表1所示。

2 線路建設(shè)時(shí)序動(dòng)態(tài)決策模型構(gòu)建

城市軌道交通線路建設(shè)時(shí)序的確定可以歸結(jié)為多屬性決策問題。考慮到在線路成“網(wǎng)”過程的不同階段中，決策者對(duì)于線路建設(shè)時(shí)序各影響因素指標(biāo)的重視程度并非一成不變，而是動(dòng)態(tài)變化的，采用Pythagorean模糊熵構(gòu)建非線性規(guī)劃模型[15，16]，確定隨著建設(shè)優(yōu)先級(jí)較高線路的建成，不同階段線路建設(shè)時(shí)序各影響因素指標(biāo)的權(quán)重，得到各階段相應(yīng)的決策矩陣，應(yīng)用理想解法計(jì)算各線路在不同建設(shè)階段的正負(fù)理想解距離，依據(jù)與理想方案貼進(jìn)度大小確定線路建設(shè)時(shí)序。

2.1 線路建設(shè)時(shí)序決策問題描述

假設(shè)城市軌交線網(wǎng)規(guī)劃近期建設(shè)n條線路，線路集為，建設(shè)時(shí)段為，不同建設(shè)時(shí)段權(quán)重集，線網(wǎng)建設(shè)時(shí)序影響因素集為，影響因素權(quán)重集。用Zij表示線路li中第j項(xiàng)影響因素相對(duì)應(yīng)的評(píng)價(jià)值，其中，。那么線路集L的原始各影響因素評(píng)價(jià)矩陣為。

通常各影響因素的評(píng)價(jià)值量綱不同，對(duì)其加以無量綱標(biāo)準(zhǔn)化處理。

2.2 確定指標(biāo)權(quán)重

線路建設(shè)時(shí)序各影響因素權(quán)重的設(shè)定，除了要兼顧各影響因素指標(biāo)間的客觀內(nèi)在聯(lián)系與專家的自身經(jīng)歷和主觀經(jīng)驗(yàn)，還需考慮到建設(shè)優(yōu)先級(jí)較高的線路實(shí)施運(yùn)營(yíng)后，對(duì)未建設(shè)的既有規(guī)劃線路后續(xù)建設(shè)時(shí)序的影響。本文引入Pythagorean模糊數(shù)的概念，用表示線路在建設(shè)時(shí)序影響因素下的指標(biāo)評(píng)價(jià)值，其中tm時(shí)段線路li對(duì)影響因素pj的滿意度用表示，線路li對(duì)影響因素pj的不滿意度用表示。

2.2.1 確定建設(shè)時(shí)段權(quán)重

本文對(duì)線路不同建設(shè)時(shí)段賦權(quán)重點(diǎn)考慮城市發(fā)展現(xiàn)狀及近期規(guī)劃，淡化對(duì)遠(yuǎn)期城市發(fā)展規(guī)劃的考量，參照文獻(xiàn)[7]，應(yīng)用泊松分布法逆形式確定權(quán)重。

則有不同建設(shè)時(shí)段權(quán)重集，其中表示tm時(shí)段的時(shí)間權(quán)重，約束條件為：。

2.2.2 確定不同時(shí)段建設(shè)時(shí)序影響因素

對(duì)于城市軌道交通線路建設(shè)時(shí)序的確定，各影響因素評(píng)價(jià)指標(biāo)的重要程度不同，在線路網(wǎng)絡(luò)化過程的不同時(shí)段，決策者對(duì)線路建設(shè)時(shí)序決策屬性的重點(diǎn)也會(huì)有所改變，因此對(duì)不同時(shí)段不同影響因素指標(biāo)賦予的權(quán)重也有一定的差別。本文對(duì)不同時(shí)段建設(shè)時(shí)序各影響因素權(quán)重的具體計(jì)算過程如下：

建立建設(shè)過程中tm時(shí)段的Pythagorean模糊決策矩陣。

計(jì)算建設(shè)過程中tm時(shí)段線路建設(shè)時(shí)序影響因素的Pythagorean模糊熵。

其中，表示對(duì)線路j屬性決策猶豫度，

構(gòu)建各時(shí)段線路建設(shè)時(shí)序影響因素權(quán)重的最優(yōu)化模型。

式中，表示tm時(shí)段線路建設(shè)時(shí)序影響因素pj對(duì)應(yīng)的屬性權(quán)重，約束條件為：。

2.3 建設(shè)時(shí)序決策矩陣

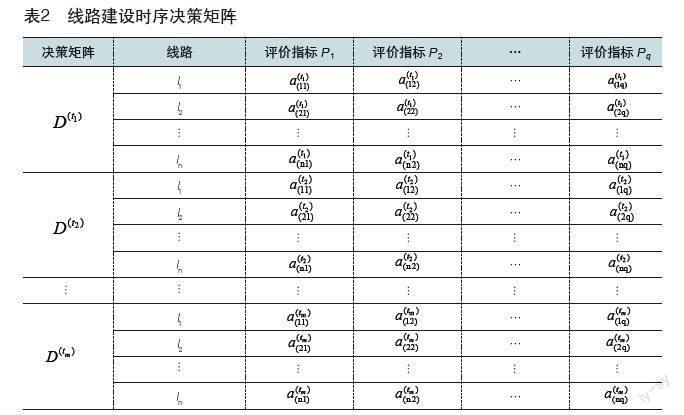
依照城市軌道交通線路建設(shè)各時(shí)段的Pythagorean模糊決策矩陣，整理可得到n條規(guī)劃線路q個(gè)影響線路建設(shè)時(shí)序指標(biāo)的m個(gè)時(shí)段的Pythagorean模糊決策矩陣，如表2所示。

2.4 線路建設(shè)時(shí)序排序決策步驟

（1）將線路建設(shè)中各時(shí)段的Pythagorean模糊矩陣整理為Pythagorean綜合模糊矩陣。

（2）依照式（3）計(jì)算建設(shè)時(shí)段權(quán)重。

（3）分別計(jì)算各時(shí)段Pythagorean模糊加權(quán)決策矩陣的正理想解方案與負(fù)理想解方案，其中。

（4）分別計(jì)算規(guī)劃中尚未確定建設(shè)時(shí)序的各條線路li在某一相同時(shí)段評(píng)價(jià)值到正理想解方案M+與負(fù)理想解方案M-的距離，本文采用歐氏距離（Euclidean distance）來度量。

（5）分別計(jì)算規(guī)劃中尚未確定建設(shè)時(shí)序的各條線路li在同一時(shí)段評(píng)價(jià)值與理想解的綜合貼進(jìn)度Ci，按照Ci數(shù)值大小排序來確定各條線路的建設(shè)時(shí)序。

3 實(shí)例分析

2020年，《重慶市城市軌道交通第四期建設(shè)規(guī)劃（2020～2025年）》獲國(guó)家發(fā)展和改革委員會(huì)批復(fù)。本文選取其中規(guī)劃第一批需要建設(shè)的9條線路（4號(hào)線西延伸段、6號(hào)線重慶東站延伸段、7號(hào)線一期、8號(hào)線一期、15號(hào)線、17號(hào)線一期、18號(hào)線渝中區(qū)延伸段、24號(hào)線一期、27號(hào)線），參照重慶市統(tǒng)計(jì)局公示的資料及各線路工程可行性客流預(yù)測(cè)與分析報(bào)告獲取交通影響指標(biāo)數(shù)據(jù)，應(yīng)用本文所構(gòu)建的動(dòng)態(tài)決策模型確定線路建設(shè)順序。

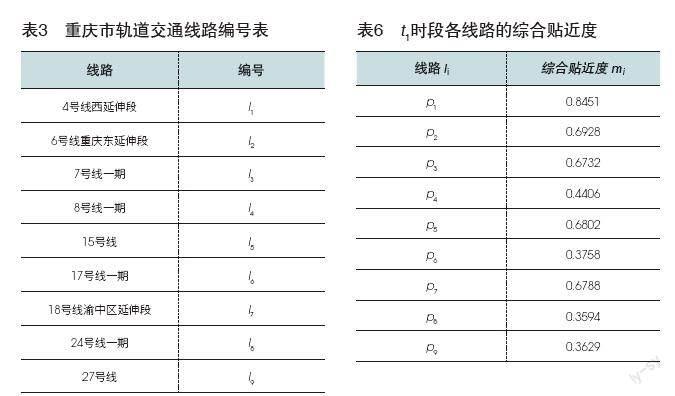
對(duì)9條線路進(jìn)行編號(hào)，如表3所示。

對(duì)線路建設(shè)時(shí)序影響因素指標(biāo)進(jìn)行無量綱標(biāo)準(zhǔn)化計(jì)算，按照式（4）、（5）、（6），得到各時(shí)段影響因素的權(quán)重，本文將這9條規(guī)劃線路建設(shè)時(shí)序劃分為4個(gè)階段，計(jì)算t1～t4各時(shí)段的Pythagorean綜合模糊矩陣，結(jié)果如表4所示。

依據(jù)式（3），令，計(jì)算得到不同建設(shè)時(shí)段權(quán)重，如表5所示。

依據(jù)各時(shí)段Pythagorean模糊加權(quán)決策矩陣和Pythagorean模糊數(shù)的基本運(yùn)算，計(jì)算時(shí)序加權(quán)矩陣，依據(jù)式（7）、（8）、（9），首先計(jì)算t1時(shí)段，規(guī)劃中各條線路l1到正理想解方案M+與負(fù)理想解方案M-的距離，計(jì)算與理想解的綜合貼近度Ci，如表6所示。

由t1時(shí)段各線路綜合貼進(jìn)度大小可知線路l1最為貼近理想解，確定最先建設(shè)線路l1。接下來計(jì)算t2時(shí)段尚未確定建設(shè)時(shí)序的各條線路li到正理想解方案M+與負(fù)理想解方案M-的距離，計(jì)算與理想解的綜合貼進(jìn)度Ci，直至t4時(shí)段。

將計(jì)算得到的各條線路li在某一相同時(shí)段評(píng)價(jià)值與理想解的綜合貼度Ci，按照綜合貼進(jìn)度Ci數(shù)值大小排序來確定各條線路的建設(shè)時(shí)序?yàn)椋簂1>l2l3l5l7> l4> l6l8l9。

《重慶市城市軌道交通第四期建設(shè)規(guī)劃（2020～2025年）》中實(shí)際規(guī)劃情況為：規(guī)劃4號(hào)線西延伸段、6號(hào)線重慶東站延伸段于2023年建成，7號(hào)線一期、15號(hào)線、18號(hào)線渝中區(qū)延伸段于2024年建成，8號(hào)線一期于2025年建成，17號(hào)線一期、24號(hào)線一期和27號(hào)線于2026年建成。

4 結(jié)語(yǔ)

（1）本文將城市軌道交通線路建設(shè)時(shí)序的確定轉(zhuǎn)化為多因素動(dòng)態(tài)決策問題，提出基于Pythagorean模糊熵的優(yōu)劣解距離法，計(jì)算各時(shí)段各線路與理想解的綜合貼近度，排序確定線路建設(shè)時(shí)序。

（2）對(duì)線路建設(shè)時(shí)序影響因素指標(biāo)賦權(quán)，兼顧各影響因素指標(biāo)間的客觀內(nèi)在聯(lián)系及專家的主觀經(jīng)驗(yàn)，并考慮到線路網(wǎng)絡(luò)化過程的不同建設(shè)時(shí)段，決策者對(duì)各影響因素重視程度不同，引入Pythagorean模糊數(shù)的概念，為不同時(shí)段影響因素指標(biāo)賦權(quán)。

（3）考慮到線路網(wǎng)絡(luò)化過程中，建設(shè)優(yōu)先級(jí)較高的線路實(shí)施運(yùn)營(yíng)后，對(duì)未建設(shè)的既有規(guī)劃線路后續(xù)建設(shè)時(shí)序的影響，將傳統(tǒng)的一次性靜態(tài)建設(shè)時(shí)序確定過程轉(zhuǎn)化為多次動(dòng)態(tài)決策，逐步計(jì)算未確定建設(shè)時(shí)序的規(guī)劃線路與理想解的綜合貼進(jìn)度，選擇相對(duì)較為迫切的建設(shè)線路。

（4）應(yīng)用所提出的線路建設(shè)時(shí)序決策方法，確定重慶市城市軌道交通第四期規(guī)劃線路建設(shè)時(shí)序，與實(shí)際規(guī)劃時(shí)序基本一致，驗(yàn)證本文所提出的決策方法具有實(shí)際應(yīng)用價(jià)值。

（5）本文所提出的城市軌道交通線路動(dòng)態(tài)建設(shè)時(shí)序確定方法只能判斷各線路的建設(shè)先后順序，無法確定規(guī)劃線路的建設(shè)時(shí)機(jī)，還有待后續(xù)深化研究。

參考文獻(xiàn)：

[1]張桐，金鍵，沈犁，等.基于灰色格序決策理論的城市軌道交通建設(shè)項(xiàng)目時(shí)序確定方法[J].城市軌道交通研究，2016，19（10）：102-105+133.

[2]張鹍鵬.節(jié)點(diǎn)重要度理論下的軌道交通線路建設(shè)時(shí)序模型分析[J].現(xiàn)代電子技術(shù)，2021，44（23）：126-129.

[3]郭延永，劉攀，吳瑤.基于累計(jì)前景理論的城市軌道交通建設(shè)時(shí)序[J].交通運(yùn)輸系統(tǒng)工程與信息，2013，13（04）：29-35.

[4]孫然然，陳家旭，李曉璐，張彭，朱廣宇.面向運(yùn)營(yíng)安全的城市軌道交通線網(wǎng)性能綜合評(píng)價(jià)[J].科學(xué)技術(shù)與工程，2020，20（36）：15067-15073.

[5]呂穎.都市圈綜合軌道交通線網(wǎng)布局評(píng)價(jià)指標(biāo)研究[J].鐵道標(biāo)準(zhǔn)設(shè)計(jì)，2021，65（04）：25-30+35.

[6]石紅國(guó)，賀玉姣.基于D-S證據(jù)理論的城市軌道交通線網(wǎng)規(guī)劃評(píng)價(jià)研究[J].鐵道運(yùn)輸與經(jīng)濟(jì)，2018，40（02）：87-93.

[7]陳德江，王君，張浩為.基于直覺模糊多屬性決策的動(dòng)態(tài)威脅評(píng)估模型[J].計(jì)算機(jī)科學(xué)，2019，46（04）：183-188.