核心素養(yǎng)下“四維一體”教學(xué)設(shè)計(jì)研究

江蘇省高淳區(qū)教師發(fā)展中心(211300) 夏繼平

義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2022 版)明確指出數(shù)學(xué)課程要培養(yǎng)學(xué)生的核心素養(yǎng).初中階段,核心素養(yǎng)主要表現(xiàn)為:抽象能力、運(yùn)算能力、幾何直觀、空間觀念、推理能力、數(shù)據(jù)觀念、模型觀念、應(yīng)用意識(shí)、創(chuàng)新意識(shí).課標(biāo)教學(xué)建議要求制訂指向核心素養(yǎng)的教學(xué)目標(biāo),以“四基”、“四能”為載體,開展以學(xué)生為中心能引發(fā)學(xué)生思考的各類教學(xué)方式進(jìn)行教學(xué).在關(guān)注“四基”、“四能”的同時(shí),特別關(guān)注核心素養(yǎng)的相應(yīng)表現(xiàn),進(jìn)行維度多元的評(píng)價(jià)[1].所以新課標(biāo)是從教、學(xué)、評(píng)三個(gè)方面全面提升的育人要求.在這樣的背景下,以課程目標(biāo)、教學(xué)目標(biāo)、學(xué)習(xí)目標(biāo)、作業(yè)目標(biāo)為一體的“四維一體”教學(xué)改革就是值得探索的落實(shí)新課標(biāo)要求的有力抓手.

“四維”就是指“課程目標(biāo)的落實(shí)”、“教學(xué)目標(biāo)的設(shè)計(jì)”、“作業(yè)目標(biāo)的匹配”、“學(xué)習(xí)目標(biāo)的達(dá)成”.就是從教學(xué)評(píng)的一致性出發(fā),打通新課標(biāo)落實(shí)的最后一公里,努力提升教師教學(xué)目標(biāo)、作業(yè)目標(biāo)、學(xué)習(xí)目標(biāo)與新課程目標(biāo)的吻合度,從而提質(zhì)增效,聚焦核心素養(yǎng)培養(yǎng),落實(shí)新課標(biāo)育人目標(biāo).下面結(jié)合七年級(jí)“利用基本模型計(jì)算角度”案例來說明:

教材蘇科版第七章三角形內(nèi)角和

課程目標(biāo)

1.理解三角形內(nèi)角、外角、中線、高線、角平分線等概念.

2.探索并證明三角形內(nèi)角和定理.掌握它的推論:三角形的外角等于于它兩個(gè)不相鄰的兩個(gè)內(nèi)角和.

3.圖形與幾何強(qiáng)調(diào)通過實(shí)驗(yàn)探究、直觀發(fā)現(xiàn)、推理論證來研究圖形,在學(xué)習(xí)的過程中提升學(xué)生幾何直觀、抽象能力、推理能力素養(yǎng).

可以看出課程標(biāo)準(zhǔn)中知識(shí)目標(biāo)很少也簡(jiǎn)單,素養(yǎng)目標(biāo)寬泛且深遠(yuǎn).在教學(xué)過程中如何落實(shí)課程目標(biāo),把素養(yǎng)目標(biāo)具象化,最終落實(shí)到學(xué)生身上,這就需要教師根據(jù)學(xué)情制定適宜的教學(xué)目標(biāo).

教學(xué)目標(biāo)

1.通過例1 中8 字型、A 型圖的學(xué)習(xí)理解三角形內(nèi)角和定理,滲透幾何直觀素養(yǎng).

2.通過例2 中鏢型圖的探究培養(yǎng)學(xué)生的自主實(shí)踐、操作能力,在觀察、猜想、推理、交流的過程中發(fā)展歸納能力,提升幾何直觀、推理能力的素養(yǎng).

3.通過變式練習(xí)鞏固、檢驗(yàn)?zāi)Ｐ偷耐茖?dǎo)應(yīng)用,幫助學(xué)生進(jìn)一步理解研究相關(guān)三角形內(nèi)角和定理和推論,以及解決問題的方法和轉(zhuǎn)換、類比的思想方法等,提升學(xué)生的幾何直觀、抽象能力、推理能力素養(yǎng).

例1.(1)如圖1,∠A,∠B,∠C,∠D之間有什么關(guān)系?

(2)如圖2,∠B,∠C,∠D,∠E之間有什么關(guān)系?

設(shè)計(jì)意圖完成三角形內(nèi)角和定理的知識(shí)目標(biāo),為引出“鏢形”問題作鋪墊.同時(shí)也是為了增強(qiáng)學(xué)生的圖形分析意識(shí),滲透幾何直觀和推理能力的素養(yǎng).考慮到問題較基礎(chǔ),所以可請(qǐng)班上基礎(chǔ)較弱或數(shù)學(xué)學(xué)習(xí)信心不足的人回答,并加以鼓勵(lì)肯定,增強(qiáng)他們的學(xué)習(xí)興趣.

例2.探究:如圖,我們將圖①所示的凹四邊形稱為“鏢形”.

求證:∠BDC=∠A+∠B+∠C.

你有幾種辦法? 請(qǐng)?jiān)趫D中示意出你的想法,并選擇其中一種進(jìn)行證明,寫出詳細(xì)證明過程.

小結(jié):____.

設(shè)計(jì)意圖角度計(jì)算是三角形內(nèi)角和幾何問題中的基本題型,很多學(xué)生在遇到問題后有很多想法但比較慌亂,或者說沒有清晰的解題思路.通過對(duì)8 字型A 型圖模型的情境探究,引出了飛鏢型的探究問題,課堂設(shè)計(jì)的問題要求學(xué)生盡可能多的想一想你有哪些分析方法,引導(dǎo)學(xué)生總結(jié)我是怎么思考的,師生共同歸納出對(duì)角度問題的探究中的一些常見思路與想法.

1.利用三角形內(nèi)角和解決問題;

2.利用三角形外角定理解決問題;

3.利用平行轉(zhuǎn)換角;

4.利用8 字型飛鏢型等模型解決問題等方法.

本題對(duì)學(xué)生理解課程目標(biāo)中三角形內(nèi)角、外角、角平分線、三角形內(nèi)角和定理及其推論有很大幫助.教學(xué)活動(dòng)時(shí)注重前提情境(學(xué)生思維中已有經(jīng)驗(yàn)也可稱為情境)分層設(shè)問,啟發(fā)引導(dǎo)各層學(xué)生說出觀察、猜想、推理、歸納等關(guān)鍵行為動(dòng)詞,進(jìn)而總結(jié)出對(duì)角度問題的探究中的一些常見思路與想法.這樣幾何直觀、抽象能力、推理能力的素養(yǎng)就伴隨著各類行為動(dòng)詞及技能方法在各層學(xué)生的思維中悄無聲息的種下、發(fā)芽、生長(zhǎng).美國課程學(xué)家古德萊德曾提出,課程的實(shí)施是一個(gè)不斷設(shè)計(jì)、多層轉(zhuǎn)化的過程,從課程標(biāo)準(zhǔn)規(guī)定的課程,到學(xué)生實(shí)際體驗(yàn)的課程,關(guān)鍵的一步在于教師對(duì)于課程的設(shè)計(jì)和實(shí)施.換句話說,落實(shí)課程的育人價(jià)值,滲透課程核心素養(yǎng)要求,關(guān)鍵在于提升教師教學(xué)設(shè)計(jì)與實(shí)施和課程目標(biāo)的吻合度.從“照著書教”,轉(zhuǎn)向“照著人教”.尊重各層學(xué)生學(xué)習(xí)規(guī)律,改變教學(xué)策略,逆向設(shè)計(jì)、精準(zhǔn)教學(xué)、聚焦素養(yǎng)、科學(xué)評(píng)價(jià).

變式練習(xí)

1.如圖①,求五角星中∠A,∠B,∠C,∠D,∠E的度數(shù)的和是____.

2.如圖②當(dāng)點(diǎn)A移動(dòng)到線段BE上,求∠CAP,∠B,∠C,∠D,∠E的度數(shù)的和是____.

3.如圖③當(dāng)點(diǎn)A移動(dòng)到如圖所示的位置,求∠CAP,∠B,∠C,∠D,∠E的度數(shù)的和是____.

設(shè)計(jì)意圖本題是五角星及它的變式模型,它的功能之一是幫助學(xué)生加深對(duì)角度問題的探究中的一些常見思路與想法的理解.了解轉(zhuǎn)換、類比等的思想方法,提升學(xué)生的幾何直觀、抽象能力、推理能力素養(yǎng).功能之二是教師通過觀察、提問、個(gè)別輔導(dǎo)等手段檢測(cè)教學(xué)目標(biāo)設(shè)置是否合理? 是否達(dá)成? 各層學(xué)生對(duì)教學(xué)目標(biāo)是否掌握? 及學(xué)生個(gè)人的學(xué)習(xí)目標(biāo)是否達(dá)成? 即學(xué)生學(xué)習(xí)目標(biāo)和教師的教學(xué)目標(biāo)“吻合度”是否一致? 對(duì)部分未達(dá)標(biāo)的學(xué)生教師可的通過引導(dǎo)啟發(fā)以及學(xué)生的合作交流等教學(xué)手段助其達(dá)成.功能之三是為教師精準(zhǔn)確定作業(yè)目標(biāo)鋪墊.

作業(yè)目標(biāo)

1.通過作業(yè)第1-3 題(略)的練習(xí),鞏固課堂學(xué)習(xí)中的探究模型,提升學(xué)生幾何直觀素養(yǎng).

2.通過作業(yè)第4 題的練習(xí),掌握內(nèi)角和定理及其推論應(yīng)用,能夠利用模型等方法解決問題,發(fā)展學(xué)生模型意識(shí)和推理能力.

3.通過作業(yè)第5 題的練習(xí),掌握角度計(jì)算常見模型及思維方式,提升學(xué)生的推理能力.

作業(yè)4.如圖,求圖中∠A,∠B,∠C,∠D,∠E,∠F的度數(shù)的和是____.

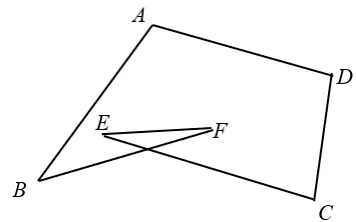
說說你的收獲:____.

作業(yè)5.如圖,我們將圖①所示的凹四邊形稱為“鏢形”.

(1)在“鏢形”圖中,∠A、∠B、∠C和∠BDC之間有怎樣的數(shù)量關(guān)系?

請(qǐng)加以證明.

利用“鏢形”圖的結(jié)論解決下列問題:

(2) 如圖②所示,BE平分∠ABD的外角∠DBM,CE平分∠ACD的外角∠DCM,BE、CE交于點(diǎn)E,若∠A=70°,∠BDC=150°,則∠BEC=____°;

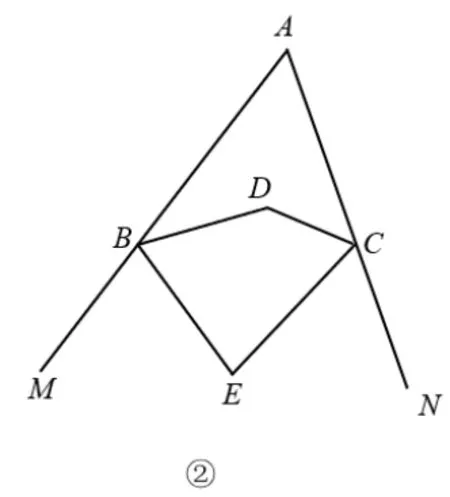
(3)如圖②所示,D是平面內(nèi)一點(diǎn),BE平分∠ABD的外角∠DBM,CE平分∠ACD的外角∠DCM,BE、CE所在直線相交于點(diǎn)E,若∠A=m°,∠BDC=n°,則∠BEC與∠BDC、∠A的數(shù)量關(guān)系為____(用含m,n的代數(shù)式表示).

設(shè)計(jì)意圖為了進(jìn)一步提升學(xué)生角度計(jì)算的能力,發(fā)展其幾何直觀和推理素養(yǎng).同時(shí)結(jié)合課堂教學(xué)中的學(xué)生表現(xiàn),精準(zhǔn)施測(cè),編制了5 道作業(yè)題.前3 題的設(shè)計(jì)是課堂學(xué)習(xí)知識(shí)模型的簡(jiǎn)單應(yīng)用,屬于屬于理解鞏固的范疇.第4 題的設(shè)計(jì)是檢測(cè)學(xué)生對(duì)角度的探究能否靈活的應(yīng)用內(nèi)角和定理及其推論的應(yīng)用,能夠利用模型等方法解決問題.作業(yè)第5題是一道綜合題,第一小問是對(duì)飛鏢形模型的證明對(duì)前面的探究有一個(gè)規(guī)范的書寫,第2 小問是對(duì)在飛鏢形的基礎(chǔ)下結(jié)合兩外角角平分線進(jìn)行一個(gè)特殊位置的計(jì)算,既是對(duì)模型的綜合應(yīng)用,也是整體思想的一個(gè)應(yīng)用.第3 小問是一個(gè)一般性的問題,通過D點(diǎn)把不同的位置,探究三角形之間的關(guān)系,是對(duì)角度計(jì)算方法的綜合應(yīng)用,對(duì)學(xué)生抽象、推理能力提升有很大的幫助.當(dāng)然本題難度較大,因此對(duì)不同層次的學(xué)生應(yīng)有不同的要求.

學(xué)習(xí)目標(biāo)學(xué)習(xí)目標(biāo)是學(xué)生通過學(xué)習(xí)所期望達(dá)到的最終目標(biāo),它是教學(xué)的起點(diǎn)和歸宿,在方向上學(xué)活動(dòng)展開起著指導(dǎo)作用,同時(shí)也是教學(xué)評(píng)價(jià)的基本依據(jù).學(xué)習(xí)目標(biāo)是不同層次的學(xué)生視角預(yù)設(shè)的,它是動(dòng)態(tài)的,不斷隨生成變化的,所以學(xué)習(xí)目標(biāo)的達(dá)成表現(xiàn)在整個(gè)教學(xué)過程中.回答的是:學(xué)生習(xí)什么? 學(xué)到什么程度? 用什么條件去學(xué)? 的問題.

本節(jié)課作業(yè)設(shè)計(jì)也是圍繞作業(yè)目標(biāo)展開的,作業(yè)目標(biāo)又是學(xué)生學(xué)習(xí)目標(biāo)、教師教學(xué)目標(biāo)以及課程目標(biāo)的落實(shí),反之則學(xué)生學(xué)習(xí)目標(biāo)、教師教學(xué)目標(biāo)、課程目標(biāo)又指引著作業(yè)目標(biāo)的設(shè)定.總之,課程目標(biāo)、教學(xué)目標(biāo)、學(xué)習(xí)目標(biāo)、作業(yè)目標(biāo)四維一體,相輔相成,相互影響,相互制約.但最終指向的就是引導(dǎo)教師向心中有人、手中有術(shù)的新型的育人方式轉(zhuǎn)變.這也是立德樹人的必然要求.