一道課本例習題變式探究

湖北省武漢市魯巷中學(430074) 熊燕

1 原題再現

例題1 (人教版教材九年級上冊P87 例4)

如圖1,⊙O的直徑AB為10cm,弦AC為6cm,∠ACB的平分線交⊙O于點D,求BC,AD,BD的長.

圖2

例題2 (人教版教材九年級上冊P90 第14 題)

如圖3,A,P,B,C是⊙O上的四個點,∠APC=∠CPB=60°,判斷ΔABC的形狀,并證明你的結論.

圖3

解析ΔABC是等邊三角形.證明如下:在⊙O中,∠BAC與∠CPB是弧BC所對的圓周角,∠ABC與∠APC是弧AC所對的圓周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴ΔABC是等邊三角形.

2 變式探究

變式1 如圖1,⊙O的直徑AB,弦AC,∠ACB的平分線交⊙O于點D,連接BC,AD,BD.求證:CA+CB=

證法一:如圖4 所示,延長CB至E,使得BE=AC,∵AB是直徑,∴∠ACB=∠ADB=90°.∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠AOD=∠BOD.∴AD=BD.又根據圓內接四邊形對角互補,∴∠CAD+∠CBD=180°,又∵∠CBD+∠EBD=180°,∴∠CAD=∠EBD,∴ΔCAD～=ΔEBD(SAS),∴CD=DE,CA=BE,∠ACD=∠BED.又∵∠ACB=∠ACD+∠BCD=90°,∴∠BED+∠BCD=90°,即∠CDE=90°,∴ΔECD是等腰直角三角形,∴CE=CB+BE=CB+CA=

圖4

(也可以如圖5 所示,延長CA至E,使得AE=CB,可證明ΔCBD～=ΔEAD,則CB=AE,再證明ΔECD是等腰直角三角形,CE=CA+AE=即CA+CB=

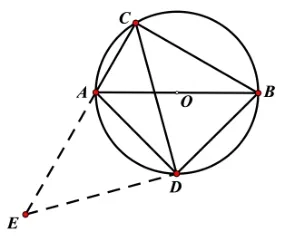
圖5

評析:從幾何圖形的變化角度思考,旋轉構造三角形全等;從等式的變化角度思考,線段的補短(線段CB往B端補短);從的數值角度思考,構造等腰直角三角形.

證法二:如圖6 所示,延長線段BC至E,使得CE=AC,連接AE.∵AB是直徑,∴∠ACB=∠ADB=∠ACE=90°.∴ΔACE是等腰直角三角形,∴∠E=∠CAE=45°,AE=∴CA+CB=CE+CB=BE,∵CD平分∠ACB,∴∠ACD=∠BCD=45°,又弧AC=弧AC,∴∠EBA=∠CDA,∠E=∠ACD=45°,∴ΔEAB～ΔCAD,即∴CA+CB=BE=

圖6

(也可以如圖7 所示,延長AC至E,使得CE=CB,可證明ΔECB是等腰直角三角形,則CA+CB=CA+CE=AE,再證明ΔCBD～ΔEBA,則即CA+CB=

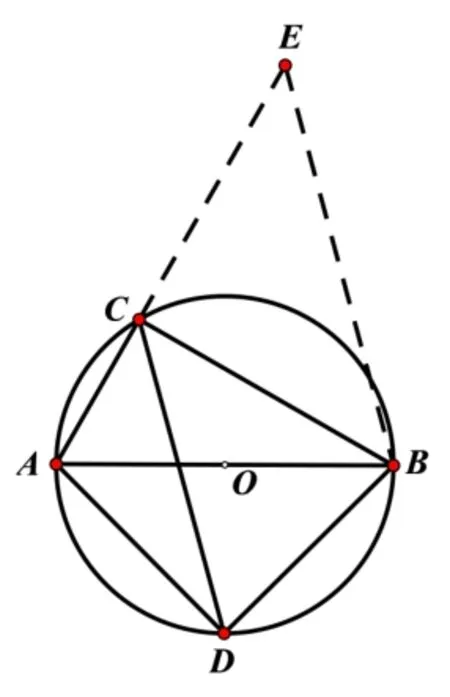
圖7

評析:從等式的變化角度思考,線段的補短(線段CB往C端補短);從的角度思考,構造等腰直角三角形;從幾何圖形的變化角度思考,旋轉構造三角形相似.

證法三:如圖8 所示,過點D分別作DE⊥CA,DF⊥CB于點E,點F,則∠AED=∠BFD=∠CFD=90°,∵AB是直徑,∴∠ACB=∠ADB=90°.∵CD平分∠ACB,∴∠ACD=∠BCD,AD=BD,DE=DF.∴RtΔADE～=RtΔBDF.∴∠ADE=∠BDF,AE=BF,又∠AED=∠ACB=∠CFD=90°,∴四邊形CEDF是矩形,又DE=DF,∴四邊形CEDF是正方形.∴CD=∴CA+CB=CE-AE+CF+BF=2CE=

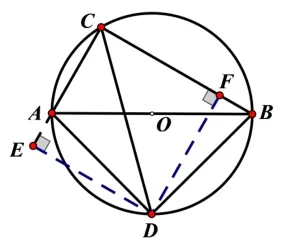
圖8

評析:當角平分線構成的等量關系與圓的知識結合時,可以轉化成“等角、等弧、等弦”互化問題,聯想角平分線性質“作垂線構全等”.

變式2 如圖9,⊙O的直徑AB,弦AC,AD,BD,BC,CD,且AD=BD,AC＜BC.求證:CB-CA=

圖9

證法一:如圖10,在線段BC上取點E,使BE=AC,連接DE.∵AB是直徑,∴∠ACB=∠ADB=90°.∵弧CD=弧CD,∴∠CAD=∠EBD.又∵AD=BD,∴ΔCAD～=ΔEBD(SAS).∴CD=DE,∠ADC=∠BDE,又∠ADB=∠BDE+∠ADE=90°,∴∠CDE=∠CDA+∠ADE=90°,∴ΔCDE是等腰直角三角形,CE=∴CB-CA=CB-BE=CE=

圖10

評析:從幾何圖形的變化角度思考,旋轉構造三角形全等;從等式的變化角度思考,線段的截長(線段CB截取BE);從的數值角度思考,構造等腰直角三角形.

證法二:如圖11,在線段BC上取點E,使CE=AC,連接DE.∵AB是直徑,∴∠ACB=∠ADB=90°.∵AD=BD,CE=AC,∴ΔADB和ΔCDE是等腰直角三角形,∠BAD=∠DBA=∠CAE=∠CEA=45°,且AB=,∴∠AEB=135°.又∵弧BD=弧BD,∴∠BCD=∠BAD=45°.∴∠ACD=∠ACB+∠BCD=135°,又∵弧AC=弧AC,∴∠ABE=∠ADC,∴ΔEAB～ΔCAD,即∴CB-CA=CB-CE=BE=

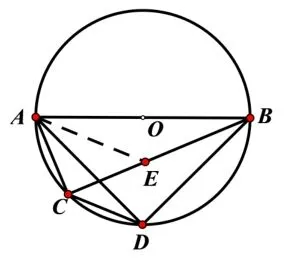
圖11

評析:從等式的變化角度思考,線段的截長(線段CB截取CE);從的角度思考,構造等腰直角三角形;從幾何圖形的變化角度思考,旋轉構造三角形相似.

變式3 已知等腰直角ΔABD是⊙O的內接三角形,∠ADB=90°.AD=BD,點C是⊙O上的點,AC＜BC.請判斷線段CA,CB,CD之間的數量關系,并說明理由.

分析根據點C是⊙O上的動點,可分兩種情況進行討論:

(1)當點C和點D分別位于直徑AB兩側時,如圖1 所示,則可證明:CA+CB=

(2)當點C和點D分別位于直徑AB同側時,如圖8 和圖12 所示,則可證明:|CB-CA|=

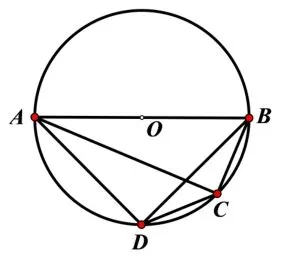
圖12

點評在數學解題活動過程中,對原題進行有層次地推進應用變式,使學生在解決問題活動中發現多個臺階或者多種途徑,從而形成多層次的活動經驗系統,培養學生的應用意識與創新意識.

變式4 (2022 年湖北省武漢市九年級元調數學第20 題)如圖3,A,P,B,C是⊙O上的四個點,∠APC=∠CPB=60°.(1) 判斷ΔABC的形狀,并證明你的結論.(2) 證明:PA+PB=PC.

解析(1)ΔABC是等邊三角形.證明如前面例2.

(2) 如圖13 所示,在PC上取點D,使PD=PA,連接AD.∵∠APC=60°,∴ΔAPD是等邊三角形.∴PA=DA,∠PAD=60°.又∵ΔABC是等邊三角形,∴AB=AC,∠BAC=60°,∴∠PAD=∠BAC=60°,∴∠BAP=∠CAD,∴ΔABP～=ΔACD,∴PB=DC,∴PA+PB=PC.

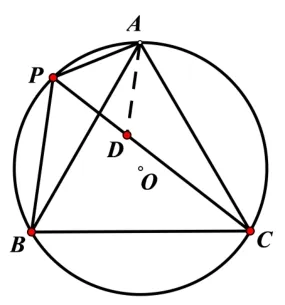
圖13

(也可以在PC上取點D,使CD=PB,連接AD.可證明ΔABP～=ΔACD,則PA=DA.再證明ΔAPD是等邊三角形,則PD=PA,∴PC=PD+DC=PA+PB.)

變式5 已知等邊ΔABC是⊙O的內接三角形,點P是⊙O上的點(不與A,B,C三點重合).請判斷線段PA,PB,PC之間的數量關系,并證明你的結論.

分析根據點P是⊙O上的動點,可分三種情況進行討論:

(1) 當點P在弧AB上時,如圖13 所示,則PC=PA+PB.(2) 當點P在弧BC上時,如圖14 所示,則PA=PB+PC.(3)當點P在弧AC上時,如圖15 所示,則PB=PA+PC.

圖14

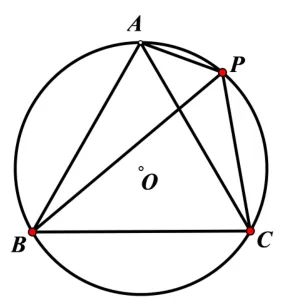
圖15

證明方法與變式4 類似.

變式6若A,P,B,C是⊙O上的四個不同點,AB=AC,∠BAC=α.請判斷線段PA,PB,PC之間的數量關系(用含α的式子表示),并證明你的結論.

分析根據點P是⊙O上的動點,可分三種情況進行討論:

(1)當點P在弧AC上時,如圖16 所示,則PB-PC=

圖16

解法一如圖17 所示,在線段PB上取點D,使AD=AP,連接AD.∵AB=AC,∴∠ABC=∠ACB,又∵弧AB=弧AB,∴∠APB=∠ACB,即∠ABC=∠APB.在等腰ΔABC和ΔADP中,∠BAC=∠DAP=α,∴∠BAD=∠CAP,又AB=AC,AD=AP,∴ΔABD～=ΔACP,∴BD=PC,PB-PC=PB-BD=PD,在等腰ΔADP中,過點A作AE⊥PD于點E,則∠DAE=∠PAE=∠DAP=α,∴PE=DE=PA×sin.∴PB-PC=2PA×sin

圖17

圖18

(2)當點P在弧AB上時,如圖19 所示,則PC-PB=2PA×sin.證明方法類似(1).

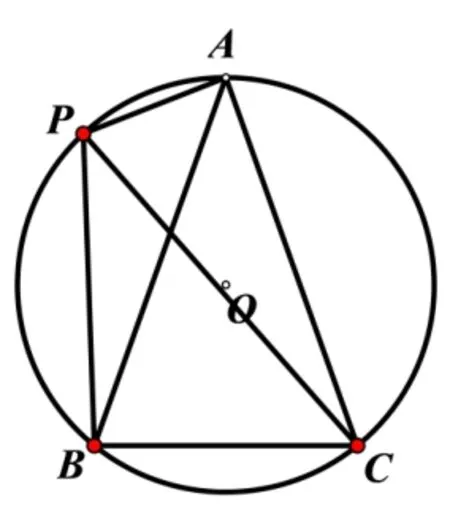
圖19

圖20

圖21

圖22

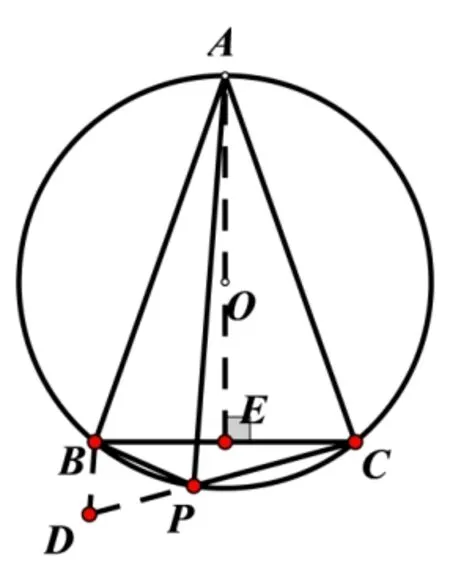
圖23

圖24

圖25

圖26

3 結語

教材中的例習題是解題的素材,要深入理解教材中習題,并引導學生深入分析,之后再進行解題的反思與歸納,從而提升學生的歸納能力.習題變式探究教學是促進有效數學學習的重要途徑,通過對數學對象(數學概念、定理、公式等)從不同角度、不同層次、不同背景進行合理的變式探究,有意識地引導學生拾級而上,從“變”的現象中發現“不變”的本質,從“不變”中探求規律,從而深化對數學知識的理解,將特殊問題一般化,使零散知識規律化,改善學生對數學的認知結構,提高識別、應變、概括能力,達到學生能“發現問題、提出問題并解決問題”的目的,從而提高應用創新能力,提升學生的數學核心素養.

總之,例習題變式探究訓練要求學生所做的習題不在于多而在于精,千題萬題源于母題(課本原題),引導學生跳出題海,融會貫通,舉一反三.習題變式探究教學使教師和學生在低消耗、低成本的教學過程中,達到教學的最優化和效果的最大化.