考慮不同充電策略的鋰電池健康狀態區間估計

張孝遠, 張金浩, 楊立新

(河南工業大學 電氣工程學院,鄭州 450001)

在碳達峰、碳中和目標背景下,電動汽車得到大力發展.鋰離子電池作為電動汽車的核心部件之一,使用量呈現井噴式增長.與此同時,由鋰離子電池健康狀態(State of Health, SOH)劣化引發的安全問題日益凸顯,在一定程度上限制了電動汽車行業的發展.SOH通過百分比的形式量化電池的老化情況,是評價電池老化程度的綜合評價標準[1].合理精確的SOH估計有助掌握電池的衰減情況,對電池安全使用、維護管理和經濟性評估都有十分重要的意義[2-3].

SOH無法通過傳感器直接測量,現有SOH評估方法主要分為模型法和數據驅動法[4].模型法基于電化學機理建立物理等效電路模型來描述鋰離子電池SOH的變化,模型參數可依據電池的不同衰退情況而變化,但鋰電池內部化學變化是一個動態、非線性的復雜電化學系統,建立準確的電化學模型非常困難[5].相較之下,數據驅動法無需考慮電池內部復雜的電化學機理,僅基于大量充放電數據提取能夠表征電池SOH的特征參數,即可建立特征參數與SOH之間的定量映射關系.因此,基于數據驅動的鋰電池SOH估計得到眾多研究者的青睞[6-7].

數據驅動法一般包含特征參數選取和SOH回歸估計兩大步驟.提取出能夠充分表征SOH的特征參數是近年來的一個研究熱點,文獻[8]中從充放電曲線中獲取增量容量(Incremental Capacity, IC)曲線,研究了IC曲線隨循環次數的變化趨勢,并驗證IC峰值、IC峰值位置等特征與SOH之間的相關性,但不同型號電池的IC峰值數量并不一致,所用特征并不適用于所用電池.文獻[9]中進一步研究不同型號電池包含多個IC峰值的情況.但在IC曲線的提取過程中必須設計復雜的濾波算法來平滑原始電壓測量值,同時,IC峰值位置會隨著電池老化而逐漸偏移;并且要獲得所有老化周期下的IC特性,需要在較大的電壓范圍內進行采樣,十分耗時.針對這個問題,文獻[10]中從放電電壓曲線及溫度曲線中獲取放電平均電壓和平均溫度作為外部特征,估算SOH.但在實際應用中,電池放電深度不一致導致平均電壓變化且溫度受環境影響較大.為此,文獻[11]中選擇從恒壓充電曲線中獲取平均電流等作為外部特征,并用等效電路模型表征恒壓曲線中的電池老化現象.上述鋰電池特征參數提取的最新研究較大程度上推動了基于數據驅動的鋰電池SOH估計的發展.但上述研究有一個共性不足——都是基于恒流恒壓充電策略下進行的鋰電池充放電實驗,所用數據均為單一充電策略下所得數據,未考慮不同充電策略或鋰電池實際放電情況等問題,在實際應用中缺乏普適性.研究高效準確的適用不同充電策略的鋰電池特征參數選擇方法是迫切的現實需求.

獲得與SOH高度相關的特征參數之后,需要建立所獲取特征參數與SOH之間的映射關系,其本質是一類多元回歸問題.諸多機器學習方法可以用于解決這類問題.反向傳播(BP)神經網絡、支持向量機、高斯回歸、決策樹等方法相繼被用來建立SOH的回歸估計模型[4].如文獻[12]中搭建BP神經網絡對鋰電池SOH進行在線估計;文獻[3]中采用粒子群優化的支持向量回歸模型實時估計不同老化狀態下的電池SOH;文獻[13]中基于高斯過程回歸(Gaussian Process Regression, GPR)建立SOH估算模型,取得較精確的估算精度;文獻[10]中搭建布谷鳥搜索支持向量模型實現鋰離子電池的SOH快速估計.結合前述特征參數選取方法,上述回歸估計模型在特定條件下能夠較為精確地估計SOH值,但上述研究所采用的SOH估計模型均為點估計方法.實際工作環境中鋰電池剩余容量存在容量回升效應[14],隨著循環次數的推移,鋰電池剩余容量會有一定幅度的波動甚至上升,導致在某一時刻的SOH估計結果無法充分揭示SOH的退化趨勢.同時,在實際運行中電動汽車工作環境復雜、負載波動較大,導致鋰電池退化模式不固定,SOH估計結果具有一定的不確定性[15],傳統點估計方法無法對鋰電池退化過程進行合理量化.

針對鋰電池SOH估計的不確定性量化估計問題,近年來有研究人員提出兩類方法來構建電池SOH的預測區間.第一類為理論方法,基于以下假設:預測誤差遵循具有零均值的確定分布,通常為正態分布或拉普拉斯分布[16].文獻[17]中開發了一個基于平均熵和相關向量機的多步預測模型,并將其應用于電池的SOH評估和剩余壽命預測,該方法基于高斯分布構造95%的預測結果置信區間.但實測的鋰電池充放電數據涉及復雜過程和噪聲干擾,很難確保滿足高斯假設.第二類為神經網絡方法,該類方法無需考慮誤差分布,因此受到研究者青睞.如文獻[18]中構建了一個改進的上下邊界估計神經網絡對鋰電池SOH進行區間估計.但此算法需要大量數據集進行訓練,而鋰電池全生命期,即SOH從100%退化到80%,一般循環次數不超過 2 000,屬于典型的小樣本問題,這類方法效果有限.

針對當前有關鋰電池SOH估計方面的研究在特征參數選取普適性和SOH估計不確定性量化兩方面的不足,提出一種適用于多種充電策略的鋰電池SOH不確定量化估計方法.該方法充分考慮當前常用充電策略下充放電曲線的變化,從電壓、電流及IC曲線中提取出多個外部特征,再通過交叉驗證方法自動選取出適用于不同充電策略的個性化最優特征組合.首次提出使用支持向量分位數回歸(Support Vector Quantile Regression, SVQR)模型進行鋰電池SOH區間估計.所采用的SVQR方法利用分位數回歸(Quantile Regression, QR)模型解決了區間分布問題,同時,支持向量回歸(Support Vector Regression, SVR)模型在小樣本充放電數據下具有較好的泛化性能.將所提方法在常用的3種不同充電策略的鋰電池數據集上進行驗證,并與QR、分位數回歸神經網絡(Quantile Regression Neural Network,QRNN)及GPR進行對比,驗證了所提方法的優越性.

1 所提方法的總體框架

所提方法的總體流程如圖1所示,分為離線訓練和在線評估兩個階段.在離線訓練階段,首先從循環電壓曲線、電流曲線及IC曲線中提取多個通用特征參數,然后采用交叉驗證方法自動選擇與SOH相關性最好的最優特征參數組合,并將其輸入SVQR模型進行訓練.在線階段將充放電數據輸入訓練好的SVQR模型,實現電池SOH的在線區間估計,從而給出鋰電池使用安全指導建議.

圖1 所提SOH區間估計方法流程Fig.1 Flow chart of the proposed SOH interval estimation method

2 考慮不同充電策略的鋰電池SOH 區間估計方法

2.1 鋰電池常用充電策略及其特點

鋰電池充電速度是制約電動汽車進一步發展的主要瓶頸之一[19].人們希望提高充電速度,但充電速度的提高會造成溫度的快速升高和電池壽命的快速衰退.因此,探索能夠兼顧充電快速性、溫度控制與合理壽命預期的充電策略一直是一個研究熱點[20].目前鋰電池充電策略已由最初的恒壓充電、恒流充電,發展到恒壓恒流充電結合的多階段充電[21].結合當前鋰電池充電策略發展的現狀,重點考慮如下3類常用的充電策略.第一類為恒流恒壓(Constant Current Constant Voltage, CC-CV)充電.CC-CV充電第一階段以恒定電流充電;當電壓達到預定值時轉入第二階段進行恒壓充電,此時電流逐漸減小;當充電電流下降到0時,蓄電池完全充滿.該充電策略可有效避免電池極化效應,但充電時間較長;第二類為恒流(Constant Current, CC)充電.CC充電采用恒定電流對電池進行充電.由于電流一般較大,電池會快速達到截止電壓,充電時間較短,但控制不得當則會增大電芯的極化;第三類為兩階段快速充電(Two Step Fast Charge, 2-step).該充電策略歷經兩個充電階段.充電過程可表達為“C1(Q1)-C2”,其中C1和C2分別代表兩個充電階段,Q1代表充電電流切換時電池的荷電狀態(State of Charge, SOC),第一個階段采用恒流充電至SOC為Q1結束;第二個階段采用CC-CV方式直至電池充滿.上述3種充電策略的電壓變化曲線如圖2所示.

圖2 不同充電策略下電壓變化Fig.2 Voltage change of different charging strategies

2.2 SOH特征選擇

鋰電池充放電曲線中蘊含豐富的電池老化信息.圖3為某單體電池不同循環次數下電壓、電流變化曲線.可見,隨著循環次數增多,充放電電壓曲線和電流曲線也隨之變化,充放電曲線的形狀與電池的老化情況高度相關.如何從充放電曲線中提取出與SOH高度敏感的特征參數是SOH估計的關鍵.但不同充電策略所對應的敏感特征參數可能不同,很難找到普適于多個充電策略的特征參數.當前有關鋰電池SOH估計方法大多針對某一特定充電策略,沒有考慮充電策略的不同及其進一步發展.為此,提出一種更泛化的特征參數提取流程.首先,充分分析不同充電策略的單體電池在不同循環次數下電壓、電流、IC曲線變化特性,并參考文獻[2,6,15]中的結論,從IC曲線提取IC曲線峰值(PIC)、IC曲線峰值對應電壓(UIC)、IC曲線峰左斜率(kL)、IC曲線峰右斜率(kR) 4個特征,如圖4(a)所示;從電流曲線提取CV充電下降到給定電流所用時間(tD)和CV充電過程最后階段的平均電流(IA),如圖4(b)所示;從電壓曲線提取CC充電上升到給定電壓所用時間(tU)和單次循環后靜置時間內的電壓回升數值(UV),如圖4(c)所示.然后,為了適應不同充電策略,采用交叉驗證方法自動選擇針對特定充電策略的個性化最優特征參數.交叉驗證方法在上述所提取的通用特征集中遍歷所有可能的特征參數組合, 然后對各個特征組合的估計結果進行排序以選出最優特征參數組合.

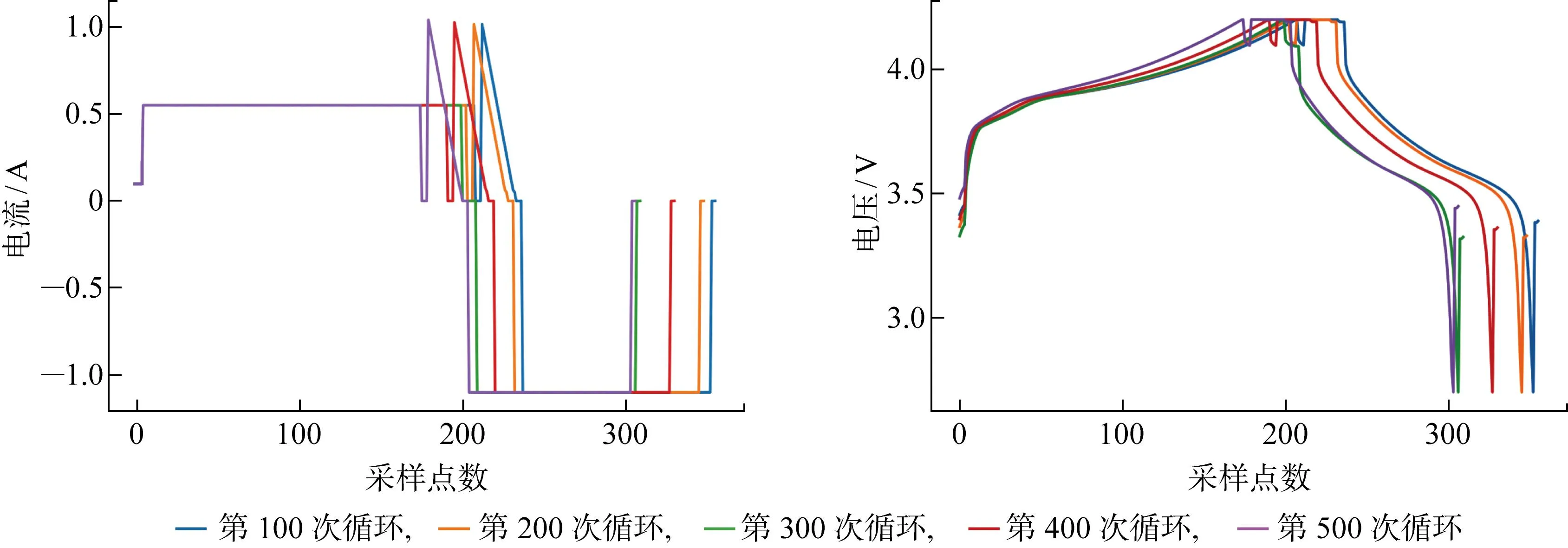
圖3 某單體電池充放電曲線在不同循環周期下的變化情況Fig.3 Change of voltage and current in charging and discharging of a single battery of different cycles

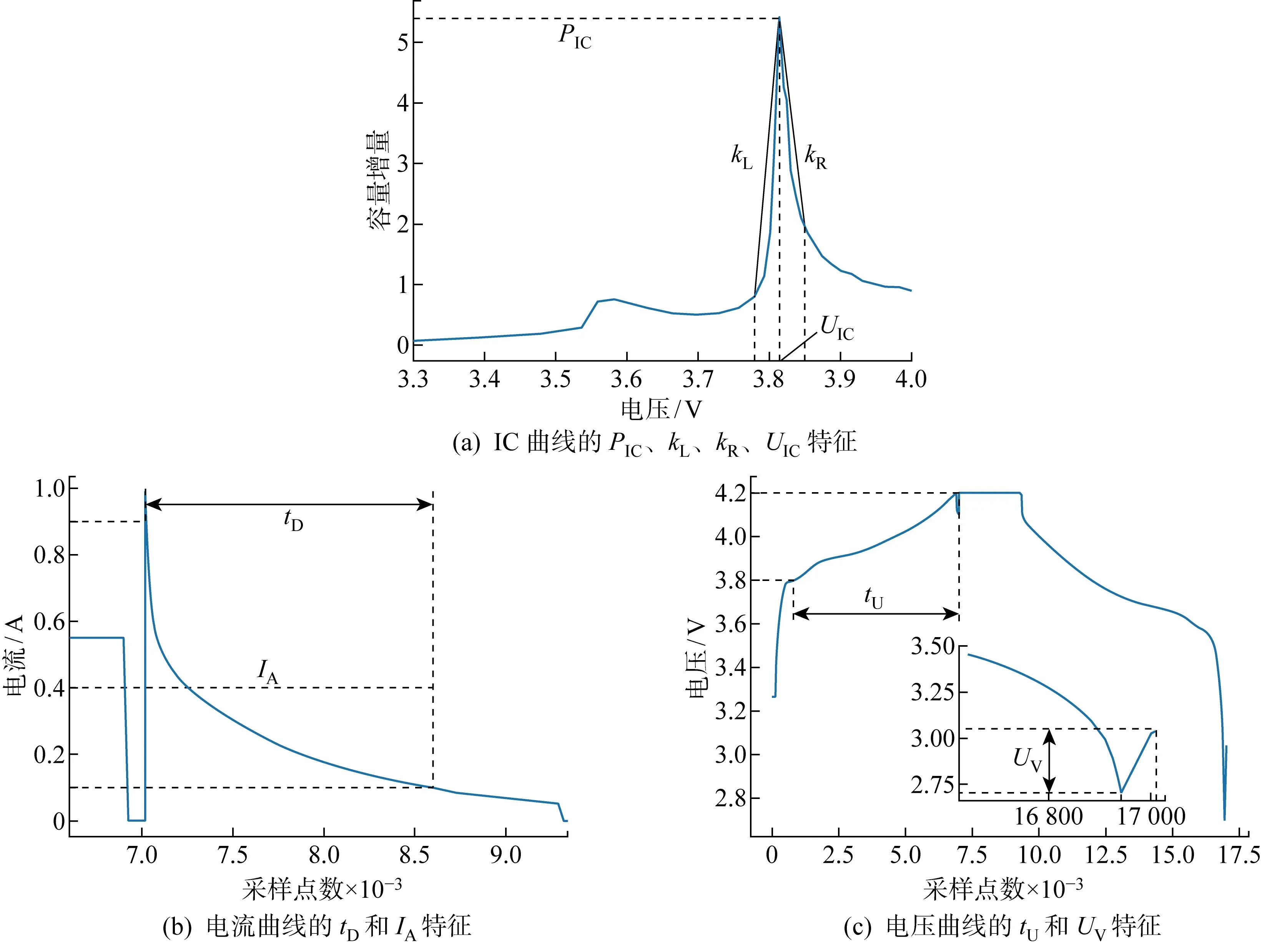
圖4 電流、電壓和IC曲線的提取特征Fig.4 Extracted features from current, voltage, and IC curve

2.3 分位數回歸

i=1, 2, …,t;τ=τ1,τ2, …,τM

(1)

式中:xi=[xi,1xi,2…xi,d]為包含d個分量的獨立變量,xi,j是xi的第j個分量,j=1, 2, …,d;yi為對應xi的因變量;qτ(xi)為因變量yi在自變量xi下的第τ分位數,對于任意分位數0<τ<1,β(τ)=[β1(τ)β2(τ) …βd(τ)]′為τ分位數下的回歸系數.β(τ)的估計值通過最小化檢驗函數ρτ(σ)獲得.

(2)

檢驗函數ρτ(σ)為一分段線性函數,定義為

ρτ(σ)=σ(τ-I(σ))

(3)

式中:I(σ)為一個指示函數,定義為

(4)

2.4 支持向量分位數回歸

(5)

(6)

s.t.yi-wTφ(xi)-b≤ξi

Shim等[25]采用半參數方法通過構造拉格朗日函數的方法對式(6)優化問題進行求解,即

(7)

(8)

式中:xs、xt為任意變量;σK為核函數的寬度.采用廣義近似交叉驗證準則[26]獲得最優超參數組合,即

(9)

3 實驗設計

3.1 實驗設置

采用3個具有不同充電策略的公開數據集來驗證所提方法的有效性.分別為馬里蘭大學高級生命周期工程中心公開數據集(簡稱CALCE)[27]、牛津電池老化數據集(簡稱Oxford)[28]和麻省理工-斯坦福-豐田研究中心電池數據集(簡稱TRI)[29].3個數據集的基本信息如表1所示,更為詳細的信息可參閱文獻[27-29].圖5分別以每個數據集中的1個電池為例,展示3個數據集各自電池容量隨循環次數的變化情況.可見盡管電池容量都隨循環次數增加而下降,但不同數據集的變化情況不同.

表1 3個數據集的基本信息Tab.1 Basic information of three datasets

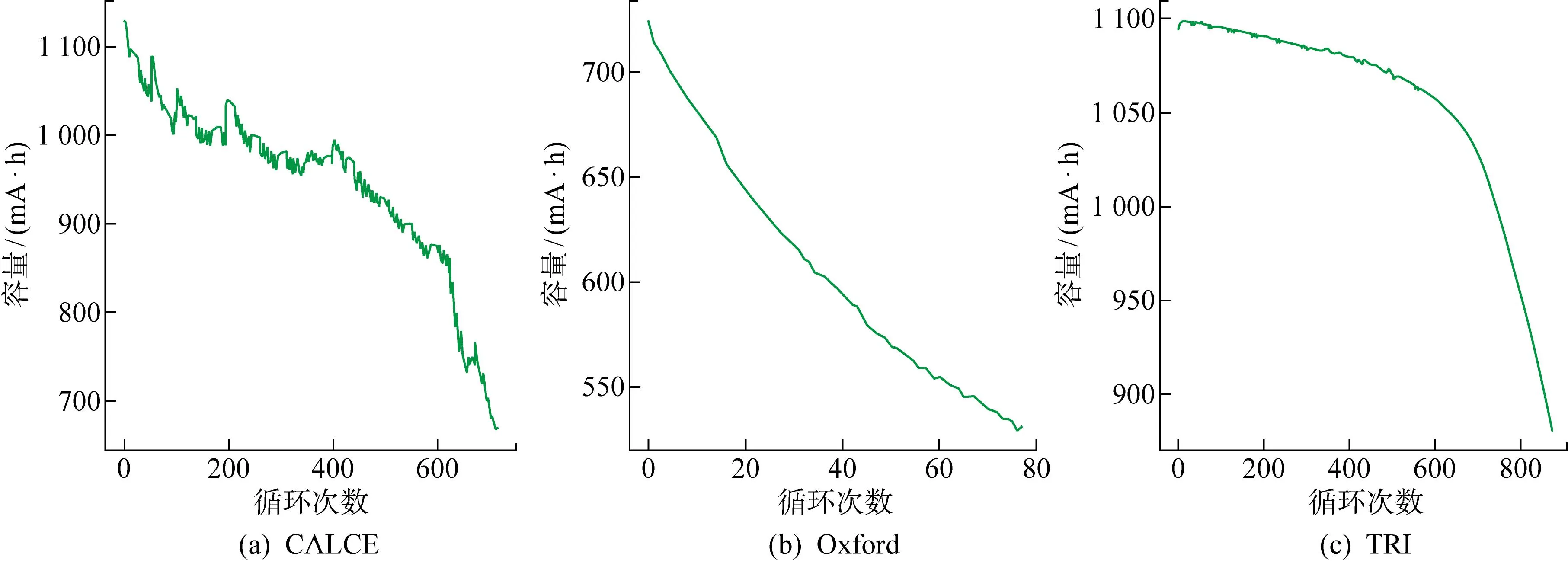
圖5 CALCE、Oxford、TRI數據集電池容量變化Fig.5 Battery capacity change of CALCE, Oxford and TRI datasets

在每個數據集中選用1個放電程度較深的單體電池充放電數據作為訓練集,在其余單體電池中任選3個作為測試集來驗證所提方法的性能.所選訓練集和測試集的情況如表2所示.

表2 訓練集和測試集情況Tab.2 Basic information of training set and test set

3.2 參與比較的方法

所提方法的優勢在于兩個方面:①可以適用于不同的充電策略;②采用的SVQR方法可以在小樣本數據集上更好地進行SOH區間估計.第一個優勢顯而易見,如文獻[13-14]的方法都針對某一特定充電策略,在遇到不同充電策略時所提取的特征參數不再適用.為此,在實驗部分重點論證所采用的SVQR相比于其他區間預測方法的優越性.首先對比SVQR與QR、QRNN,QR把分位數的概念融入普通的線性回歸中,本質上是一種線性方法;QRNN將分位數概念與神經網絡結合以解決非線性回歸問題.此外,最近GPR被報道在處理鋰電池SOH區間估計方面具有優秀性能[15],因此還將SVQR方法與GPR方法進行對比.

3.3 評價指標

為全面驗證所提方法的性能,采用如下3個指標來評價SOH區間估計結果的優劣:平均區間分數(Average Interval Score, AIS)[30]、平均預測區間中心偏差(Mean Prediction Interval Center Deviation, MPICD)[31]以及平均絕對百分比誤差(Mean Absolute Percentage Error,MAPE)[32].上述指標包含對估計結果區間寬度、區間覆蓋率以及估計偏差等信息的衡量,各自定義如下:

(1) AIS指標.AIS指標定義為所有區間估計點的區間分數均值,可綜合衡量區間覆蓋率和區間寬度,其值越大越優,按下式計算.

(10)

式中:α為置信區間寬度;Ntest為測試集電池循環次數;S(α)(xi)為第i個估計區間的區間分數,定義為

S(α)(xi)=

(11)

(2) MPICD指標.MPICD表示預測區間中心位置與實際值的偏差,該值越小越優,按下式計算.

(12)

(3) MAPE指標.MAPE按下式計算,該指標可衡量預測區間的寬度信息,狹窄的區間比寬大的區間更好.

(13)

式中:Li、Ui分別為預測下限和上限.

4 實驗結果與分析

經過特征提取和交叉驗證特征自動優選過程,最終對CALCE數據集選擇IC曲線峰值、IC曲線峰值對應電壓、IC曲線左斜率、CC充電上升到給定電壓所用時間、CV充電下降到給定電流所用時間5個特征;對Oxford數據集選擇IC曲線峰值、IC曲線左斜率、IC曲線右斜率3個特征;對TRI數據集選擇IC曲線峰值、IC曲線右斜率、CV充電下降到給定電流所用時間3個特征.為了實驗對比的公平性,其余3種方法在評估時針對不同的數據集采用與SVQR方法同樣的特征參數.表3～5分別展示所提方法與QR、QRNN和GPR方法分別在CALCE、Oxford和TRI數據集中各自任選的3個單體電池上的SOH評估結果,其中用粗體標出的為最優結果.圖6～8分別展示4種方法在3個數據集中CS35、Cell7、b0c32這3個電池上的SOH估計效果.

首先,從圖6～8和表3～5可以看出,在所有數據集上,對于所有的評價指標QRNN與QR結果比較接近,但都遠劣于SVQR;QRNN略優于QR,這印證了QR本質上是線性回歸方法,其在處理鋰電池SOH非線性估計上性能不足.而QRNN性能遠劣于SVQR,這充分印證了在本文數據集的量級上,SVQR處理小樣本非線性問題時具有更好的泛化能力.其次,在所有實驗中SVQR方法的結果與GPR接近,但在多數電池上多數指標都優于GPR方法.尤其在MAPE指標方面,SVQR方法在所有數據集上全優于GPR.AIS指標方面,SVQR方法在Oxford和TRI數據集上均取得最好結果,僅在CALCE數據集上,劣于GPR方法;MPICD指標方面,SVQR方法在CALCE和Oxford數據集上除Cell7電池外,均明顯優于GPR,僅在TRI數據集上略劣于GPR.文獻[15]報道,GRP方法是目前處理鋰電池SOH估計的最優方法.但實際上,GPR需要假設數據服從高斯分布,而實測的鋰電池充放電數據涉及復雜過程和噪聲干擾,很難確保滿足高斯假設.本文所提SVQR則無需此假設,這可以解釋上述實驗中SVQR總體優于GPR的原因.另外值得指出的是,實驗采用同一充電協議下的某一放電深度較深電池的全生命期循環充放電數據來訓練SVQR模型,用同數據集中其他電池來測試,這與其他多數研究采用同一電池的部分充放電數據來預測其剩余循環的退化情況相比更有實際意義.上述結論充分證明本文方法在SOH估計方面的優勢.

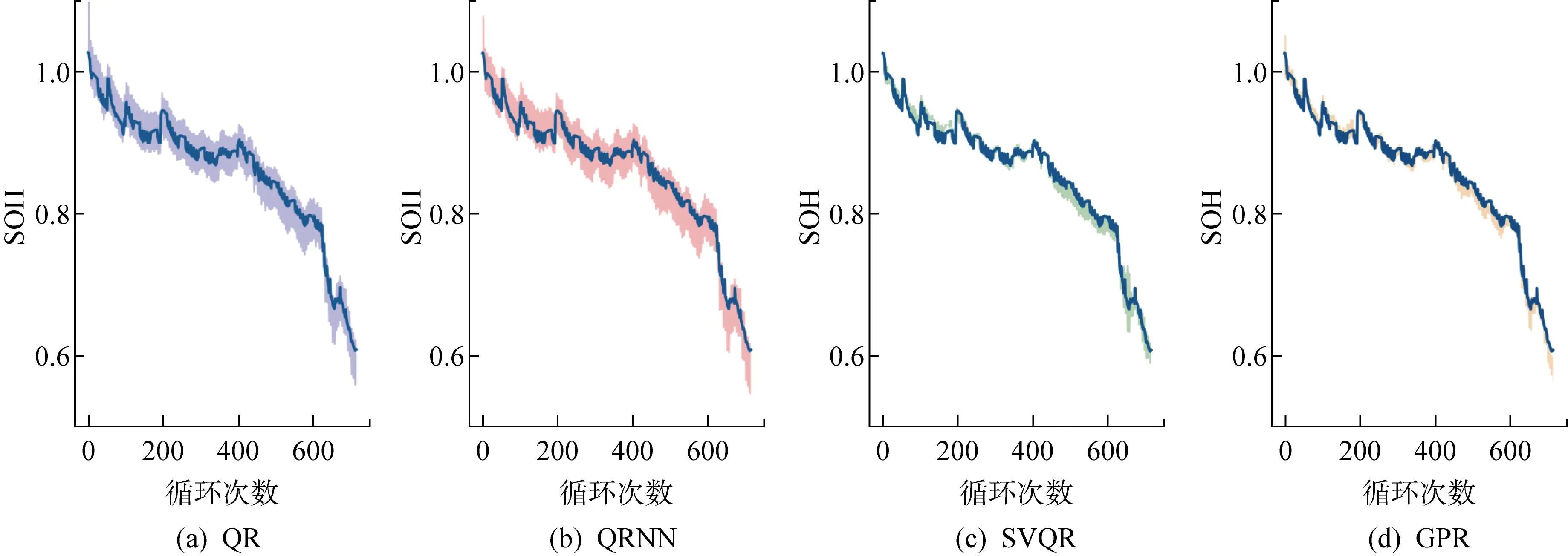
圖6 4種方法在CALCE數據集CS35電池的SOH區間估計對比結果Fig.6 Comparison of four methods for estimating SOH interval of CS35 battery in CALCE dataset

圖7 4種方法在Oxford數據集Cell7電池的SOH區間估計對比結果Fig.7 Comparison of four methods for SOH interval estimation of Cell7 battery in Oxford dataset

圖8 4種方法在TRI數據集b0c32電池的SOH區間估計對比結果Fig.8 Comparison of four methods in estimating SOH interval of b0c32 battery in TRI dataset

表3 CALCE數據集3個單體電池的SOH估計對比結果Tab.3 Comparison of SOH estimation of three single cells in CALCE dataset 10-3

5 結論

提出一種考慮不同充電策略的鋰電池剩余容量SVQR區間估計方法.該方法在離線階段,從鋰電池充放電電壓、電流及容量增量曲線中獲取多個特征,并采用交叉驗證方法自動選擇最優特征組合.選取放電程度較深的單體電池循環充放電數據訓練SVQR模型.在SOH在線估計階段,采用和訓練模型相同的特征作為模型輸入,對服役中的鋰電池進行SOH區間估計.最后在3個采用不同充電策略的數據集驗證所提方法,并與QR、QRNN和GPR方法進行對比,可得出以下結論:

(1) 在不同充電策略下,利用相同外部特征對于鋰電池SOH的估計結果也不同.采用兩步特征提取策略,即首先針對不同充電策略提取足夠多特征,再選取針對不同電池及充電策略的個性化特征參數,可以顯著提高電池SOH估計的精度,且具有良好的普適性.

(2) 神經網絡類方法的訓練需要較大數據集樣本,但在樣本量有限的鋰電池充放電數據集中神經網絡類算法估計效果有限.而SVQR利用SVR算法適用于小樣本數據集的特點,即使是在小樣本條件下也可以較好地在置信區間內估計鋰電池SOH.

(3) 相較于文獻報告的當前最優的GPR方法,所提SVQR方法無需原始數據服從高斯分布,可在一定置信區間內實現較好的SOH估計結果,具有更好的適應性和魯棒性.