一種整數(shù)抽取結(jié)合小數(shù)插值重采樣技術(shù)研究
單長勝,尹曙明,鄭哲,郝利云
(1.北京空間信息傳輸中心,北京 102300;2.北京理工大學(xué),北京 100081)
0 引 言
射頻直采是指將天線接收到的射頻信號經(jīng)過限幅、濾波、放大后直接送入高速ADC 采樣,其降低了系統(tǒng)的硬件復(fù)雜度,減少了模擬器件引入的噪聲,改善了通道的一致性。近年來隨著相控陣?yán)走_(dá)、高速信號轉(zhuǎn)換及信號處理等技術(shù)的飛速發(fā)展,促進(jìn)了射頻直采技術(shù)的逐步工程應(yīng)用。然而射頻直采信號數(shù)據(jù)率極高,導(dǎo)致后續(xù)信號傳輸與處理難度大幅上升[1]。數(shù)字重采樣技術(shù)是緩解數(shù)字信號處理壓力的重要手段,采用數(shù)字重采樣技術(shù)可以降低射頻信號采樣率,進(jìn)而有效地實現(xiàn)信號的傳輸、處理和存儲。
數(shù)字重采樣可分為整數(shù)倍重采樣與分?jǐn)?shù)倍重采樣兩類[2]。整數(shù)倍重采樣包括整數(shù)倍抽取與內(nèi)插,相關(guān)理論成熟。分?jǐn)?shù)倍重采樣包括簡單分?jǐn)?shù)重采樣與基于小數(shù)插值的數(shù)字重采樣。簡單分?jǐn)?shù)重采樣采用抽取級聯(lián)內(nèi)插的方式實現(xiàn)分?jǐn)?shù)倍采樣率轉(zhuǎn)換,但該方法僅適用于分子分母較小的場景,無法解決固定射頻采樣率下精確變采樣率變換的需求;基于小數(shù)插值的數(shù)字重采樣方法多采用分段多項式插值逼近理想低通濾波器,對信號直接進(jìn)行小數(shù)插值,從而實現(xiàn)任意倍采樣率轉(zhuǎn)換。基于小數(shù)插值的數(shù)字重采樣方法靈活性高、適用性強,在信號處理領(lǐng)域得到了廣泛應(yīng)用。整數(shù)倍重采樣只適用于射頻采樣率與目標(biāo)采樣率成整數(shù)倍的場景,具有很大的局限性。簡單分?jǐn)?shù)重采樣實現(xiàn)簡單,但無法處理大分子分母的復(fù)雜分?jǐn)?shù)倍重采樣。基于小數(shù)插值的數(shù)字重采樣方法理論上雖然可以實現(xiàn)任意倍采樣率轉(zhuǎn)換,然而對射頻采樣信號直接進(jìn)行小數(shù)插值時,需要在射頻采樣率下對信號進(jìn)行實時處理,難度大,尤其是當(dāng)射頻采樣頻率幾個GHz 時,往往需要幾十路進(jìn)行并行處理,且每路均需小數(shù)插值運算,將直接導(dǎo)致工程中幾乎無法實現(xiàn)。此外,基于小數(shù)插值的數(shù)字重采樣方法多采用Farrow 結(jié)構(gòu)實現(xiàn),然而Farrow 結(jié)構(gòu)內(nèi)插濾波器面對大抽取因子時,帶外噪聲濾除能力差,低信噪比條件下將直接導(dǎo)致重采樣輸出信號品質(zhì)惡化。綜上,本文提出了一種整數(shù)抽取結(jié)合小數(shù)插值重采樣法來實現(xiàn)任意倍數(shù)字重采樣方法的轉(zhuǎn)換。
1 整數(shù)抽取結(jié)合小數(shù)插值的數(shù)字重采樣方法
考慮到直接采用并行結(jié)構(gòu)小數(shù)插值數(shù)字重采樣將極大的消耗資源[3],且無用的帶外噪聲抑制差,本文給出一種整數(shù)抽取結(jié)合小數(shù)插值的數(shù)字重采樣方法。采用該方法首先可有效地降低數(shù)據(jù)率,減少并行處理難度,節(jié)省乘法器資源;其次,采用該方法因先進(jìn)行了整數(shù)抽取,直接地降低了小數(shù)插值的輸入數(shù)據(jù)率,從而將Farrow 結(jié)構(gòu)內(nèi)插濾波器頻率響應(yīng)降低,可提高對帶外噪聲的濾除能力。整數(shù)抽取結(jié)合小數(shù)插值的數(shù)字重采樣結(jié)構(gòu)如圖1所示。

圖1 整數(shù)抽取結(jié)合小數(shù)插值數(shù)字重采樣示意圖
圖1中,x(NsnTs),x((Nsn+1)Ts),…,x((Nsn+N- 1)Ts)為輸入數(shù)據(jù),h(Ns∕2 - 1)…h(huán)(j)…h(huán)(0)為半帶濾波器系數(shù),g(nThb)為半帶抽取后輸出,c0(-N∕2),c0(-N∕2 + 1),…,cM(N∕2 - 1) 為小數(shù)延時濾波器系數(shù),un為當(dāng)前輸入采樣點時刻與下一個重采樣點輸出時刻的時間間隔除以輸入采樣周期。log2D級整數(shù)抽取采用半帶濾波器對多路并行信號進(jìn)行抽取濾波。濾除大量帶外噪聲的同時將射頻采樣率fs降為fhb;多級整數(shù)抽取后,在低采樣率下采用Farrow 結(jié)構(gòu)將小數(shù)插值采樣率變換為目標(biāo)采樣率fsb。fs、fhb與fsb滿足
2 整數(shù)抽取結(jié)合小數(shù)插值重采樣理論模型
假設(shè)Thb=DTs,Tsb=(1 +p)Thb,則Tsb=D(1 +p)Ts。其中D為整數(shù),0 <p<1,Ts、Thb與Tsb分別為射頻采樣周期、多級抽取濾波后采樣周期以及基帶采樣周期。x(nTs)經(jīng)抗混疊濾波器濾波得到
其中,hD(t)為抗混疊濾波器沖激響應(yīng),等效為多級濾波器級聯(lián),即濾波器頻率響應(yīng)HD(ejw)滿足下式:
式中,Hhbi(ejw)為第i級抗混疊濾波器頻率響應(yīng),將x'(nTs)進(jìn)行D倍抽取得到
經(jīng)抽取后采樣率變?yōu)閒hb,采用Farrow 結(jié)構(gòu)進(jìn)行1 +p倍的小數(shù)插值,因此采用分段多項式插值逼近理想低通濾波器時,分段多項式間隔變?yōu)門hb。其基函數(shù)化為
對g(nThb)進(jìn)行小數(shù)插值可以得到
式中,N′1= -N∕2,N′2=N∕2 - 1。將式(4)代入式(8)可以得到
上式即為整數(shù)抽取結(jié)合小數(shù)插值數(shù)字重采樣理論模型[4-5]。
2.1 整數(shù)抽取結(jié)合小數(shù)插值參數(shù)遞推解算方法
多級整數(shù)抽取后,一般并行多路信號只剩一路。直接進(jìn)行串行時間參數(shù)遞推即可。由式(9)可知,輸出采樣點所需時間參數(shù)um為
同樣采取在小數(shù)插值輸入時鐘域下更新時間參數(shù)un,則將Tsb=(1 +p)Thb代入下式:
由un的物理意義可知,un∈[0,1 +p),因此上式可以轉(zhuǎn)化為
2.2 多級整數(shù)抽取濾波器選擇
典型的多級抽取濾波采用CIC 作為前級濾波器,因其系數(shù)全為1,無乘法計算,但當(dāng)處理射頻直采信號時,將CIC放在第一級會存在以下問題:
1)反饋遞歸結(jié)構(gòu)并行實現(xiàn)難度大及數(shù)據(jù)溢出
CIC 的典型結(jié)構(gòu)由積分器和梳妝濾波器構(gòu)成,如圖2給出的CIC濾波器的3級級聯(lián)結(jié)構(gòu)。積分器是一種帶有反饋的遞歸結(jié)構(gòu),F(xiàn)PGA 實現(xiàn)時無法使用并行的方法降低積分器的工作頻率,這就決定了該結(jié)構(gòu)極其不適用于射頻直采輸出高速率信號的前級濾波。在數(shù)字濾波過程中,積分器不斷累加,積分器輸出信號逐漸增大,存在輸出信號位寬確定的情況下數(shù)據(jù)溢出的問題,需要采用等時間間隔的復(fù)位在數(shù)據(jù)溢出前對積分部分的寄存器進(jìn)行復(fù)位,增加了濾波器設(shè)計的復(fù)雜度。

圖2 CIC抽取濾波器三級級聯(lián)結(jié)構(gòu)
2)CIC通帶衰減問題
CIC 濾波器的直接實現(xiàn)結(jié)構(gòu)雖然不存在反饋遞歸結(jié)構(gòu),但單級CIC 濾波器阻帶衰減小,無法有效地濾除帶外量化噪聲及其他噪聲,若采用多級級聯(lián)方式,通帶衰減又會增大,當(dāng)寬帶信號經(jīng)過CIC 低通濾波,可能會造成信號頻譜的惡化,尤其是對于調(diào)制信號來說,惡化的頻譜會嚴(yán)重影響系統(tǒng)的性能[6]。通常采用CIC 濾波器與內(nèi)插二階多項式(Interpolated Second Order Polynomial, ISOP)級聯(lián)的方法減少通帶的衰減。但通過級聯(lián)ISOP補償濾波器改善通帶衰減,就必須付出更多的級數(shù),這樣就失去了CIC 濾波器相對于半帶濾波器和FIR濾波器的最大優(yōu)勢。
綜上,射頻直采信號采用CIC作為多級抽取濾波器有著諸多劣勢。而半帶濾波器不存在反饋結(jié)構(gòu),可以通過并行處理及流水線技術(shù)實現(xiàn)高速抽取濾波,且其近一半系數(shù)為零,減少了近3∕4 的乘法運算和近一半的加法運算,另外,半帶濾波器還具有通帶平坦度高、阻帶衰減大的優(yōu)點,在進(jìn)行抽取濾波運算時,不會造成信號頻譜的惡化及重疊。因此,綜合考慮本文采用半帶濾波器作為多級抽取濾波器。
3 仿真驗證
仿真實驗1:輸入帶寬為8 MHz,載波中心頻率2 250 MHz 線性調(diào)頻信號,以射頻采樣率3 GS/s 采樣輸出16 路并行信號,對16 路并行信號正交下變頻后,首先以7級14階半帶濾波器對其進(jìn)行128倍抽取濾波,將采樣率降到23.437 5 MS/s;然后經(jīng)3階拉格朗日插值的Farrow 結(jié)構(gòu)將采樣率轉(zhuǎn)換為20.48 MS/s。仿真結(jié)果如圖3所示。
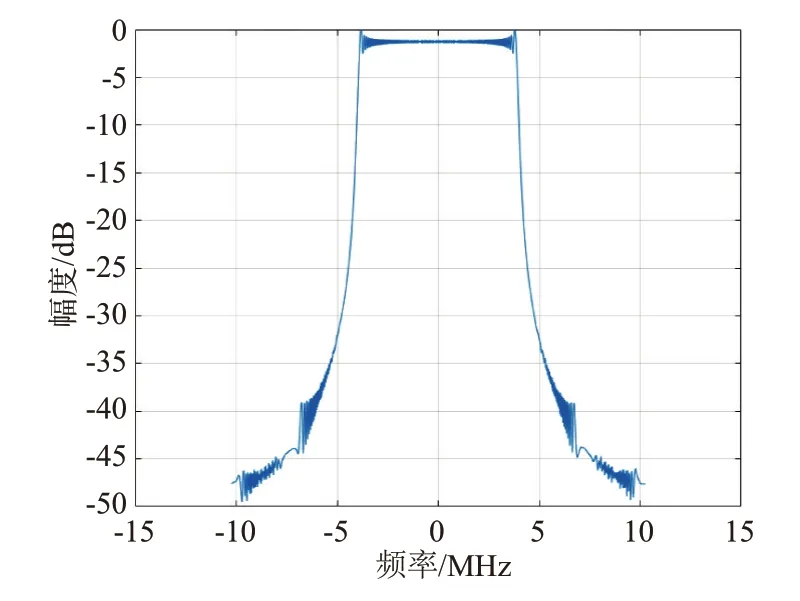
圖3 整數(shù)抽取結(jié)合小數(shù)插值重采樣輸出信號頻譜
實驗表明,整數(shù)抽取結(jié)合小數(shù)插值的重采樣方法,有效融合了整數(shù)采樣技術(shù)的成熟高效優(yōu)勢和小數(shù)插值的靈活性優(yōu)勢,兼顧了射頻直采的復(fù)雜性和靈活性需求,具備工程可行性。
仿真實驗2:分別輸入信噪比為30,10,0和-10 dB 的線性調(diào)頻信號,信號參數(shù)及抽取濾波操作與實驗1 相同,在4 種信噪比下的仿真結(jié)果如圖4所示。
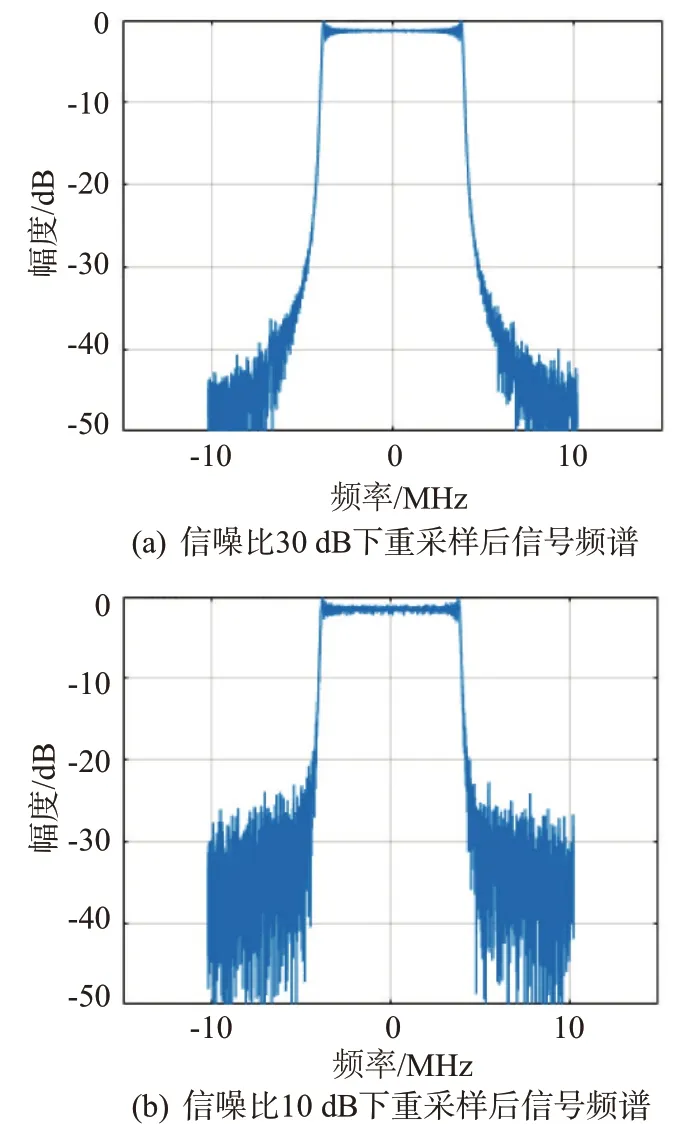
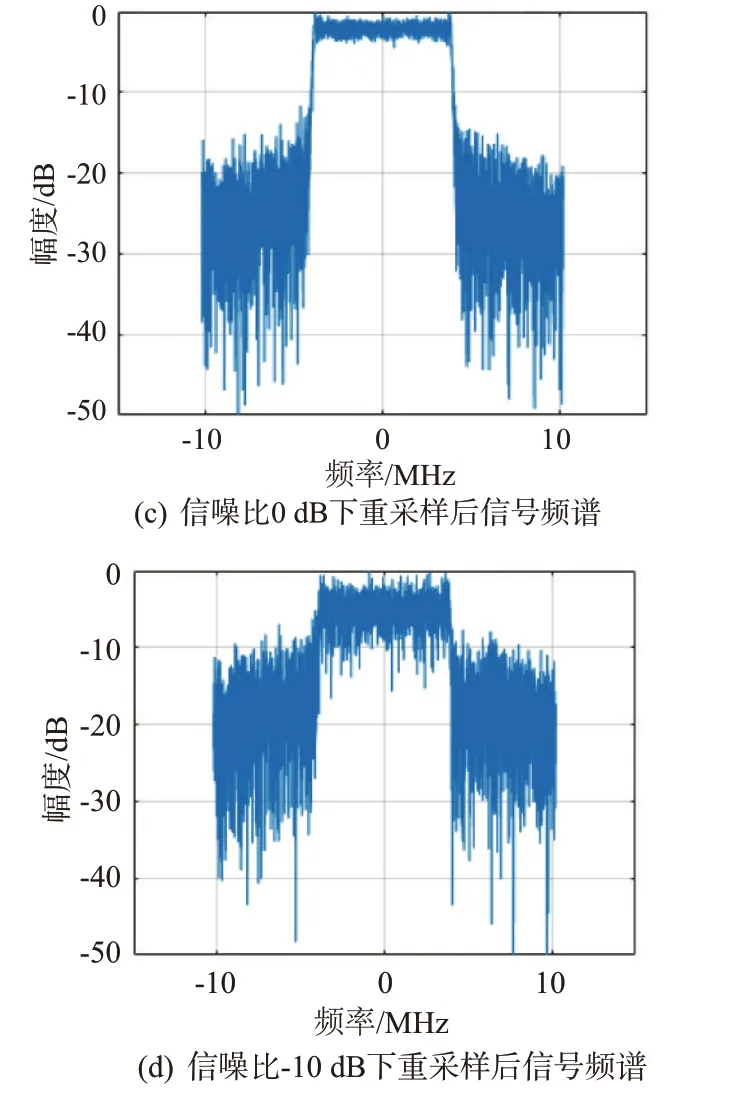
圖4 不同信噪比下整數(shù)抽取結(jié)合小數(shù)插值重采樣輸出信號頻譜
實驗表明,本方法在0 dB 信噪比情況下,仍具備較好的重采樣輸出信號品質(zhì),可應(yīng)用于低信噪比條件下的信號采樣。
4 結(jié)束語
本文針對射頻高速率采樣需求,開展了數(shù)字重采樣技術(shù)研究,提出一種整數(shù)抽取結(jié)合小數(shù)插值的數(shù)字重采樣方法。由理論與仿真結(jié)果可知,該方法可以實現(xiàn)射頻信號復(fù)雜分?jǐn)?shù)倍數(shù)字重采樣精確調(diào)整。且通過整數(shù)抽取將小數(shù)插值濾波器的輸入采樣率降低,使得Farrow 內(nèi)插濾波器的頻率響應(yīng)零點接近于目標(biāo)采樣率,改善了帶外噪聲濾除能力。在信噪比相同的情況下,整數(shù)抽取結(jié)合小數(shù)插值的數(shù)字重采樣輸出信號質(zhì)量更好。
與傳統(tǒng)整數(shù)結(jié)合簡單分?jǐn)?shù)抽取相比,該方法可實現(xiàn)大范圍精確變采樣率變換,具有更大的普適性。與直接小數(shù)插值方式進(jìn)行變采樣率相比,可極大地降低后續(xù)信號處理的并行度,且改善了帶外噪聲。

