含氫儲能的獨立微電網IGDT魯棒規劃

肖白,韓康琦,張曉華

(1. 東北電力大學電氣工程學院,吉林省吉林市 132012; 2. 國網吉林省電力有限公司延邊供電公司,吉林省延吉市 133000)

0 引 言

隨著經濟的快速發展,能源危機和環境污染問題日益突出,如何提高能源利用效率、發掘可再生能源、推進可再生能源生產是亟需解決的關鍵問題[1]。在此背景下,以可再生能源和儲能技術構建的微電網逐漸興起,微電網技術成為促進可再生能源接入和消納的重要手段[2-3]。

在微電網規劃設計階段,有效合理地配置內部設備的容量可以確保微電網發揮良好的運營效果[4]。文獻[5]計及了可靠性成本,使用改進二階振蕩粒子群算法求解系統容量配置。文獻[6]以系統年均總費用和可再生能源利用率為目標函數,建立了微電網容量隨機優化配置模型。文獻[7]討論了蓄電池充放電次數和深度對壽命的影響,研究并網型微電網的容量配置。然而,以上研究中微電網的儲能主要依賴于電池,但其壽命短暫且價格昂貴,存在環境污染,使微電網的發展受到一定限制。

已有研究發現氫儲能有著清潔、高效、能量密度大、容量大的優點,兩者具有一定的互補特性[8-9]。文獻[10]提出一種電-氫混合儲能孤島直流微電網能量管理方法,引入成本和等效氫耗最小算法,對系統進行優化控制。文獻[11]針對具有電解制氫的獨立微電網,在限制最大容量和碳排放上進行了優化。文獻[12]分析電熱聯供和氫儲能的優勢,提出了一種以氫儲能作為能量轉換樞紐的園區綜合能源系統優化配置模型。文獻[13]引入階梯碳交易機制,研究了含氫儲能的并網型微電網的容量優化問題。但上述研究均是在確定性場景下進行的,并未考慮風光不確定性[14]對規劃結果的影響。

而現如今,對不確定性問題的研究方法主要有魯棒規劃法[15]和隨機規劃法[16],但都存在一定局限性,前者需要精確的不確定集合,后者則依賴確定的概率分布且計算量過大。對此,文獻[17]提出了信息間隙決策理論(information gap decision theory,IGDT),其無需知道不確定參數的詳細概率分布,能夠在保證求解結果不遜于預設目標的情況下,最大化不確定變量的波動范圍,從而可最大化規避不確定性對求解結果的影響。文獻[18]建立IGDT魯棒與機會模型,解決電力系統調度中的“奈特式不確定性”問題。目前,基于IGDT的不確定性處理在機組組合[19-20]、虛擬電廠優化[21-22]等方面展開,但是用于微電網規劃方面的研究較少。

此外,對于含高滲透比例可再生能源的微電網而言,通過給予用戶一定的經濟激勵,鼓勵用戶自主參與需求響應(demand response,DR),有助于協調源荷,減少系統儲能需求,提升經濟效益[23-25]。文獻[26]建立了動態電價經濟模型,減少發電和負荷曲線之間的不匹配。文獻[27]針對多微網系統,建立了自主競價機制的分布式需求響應模型。然而,目前關于微電網優化規劃的研究大多只考慮不確定性或DR,在同時考慮不確定性和激勵型DR方面相對薄弱。而在對獨立微電網進行規劃時,若同時考慮風光出力不確定性和激勵型DR,能夠在保證供電可靠性的前提下進一步提高經濟性。

綜上所述,本文提出一種基于IGDT的含氫儲能的獨立微電網優化規劃方法。首先,建立含氫儲能的獨立微電網基本結構,并對其運行原理加以說明;其次,針對風光出力的不確定性,引入IGDT進行模擬,以微電網年投資成本和年運行成本之和最小為目標,建立綜合考慮不確定性和激勵型DR的雙層魯棒優化規劃模型來計算微電網的最優規劃結果;最后,以某地區微電網為例來驗證本文模型的有效性與合理性。

1 含氫儲能的獨立微電網模型

1.1 獨立微電網的結構

本文所提獨立微電網結構包括光伏陣列(photovoltaic cell, PV)、柴油機組(diesel generator, DEG)、風電機組(wind turbine, WT)、負荷和由儲氫罐、燃料電池和電解槽組成的氫儲能系統。氫儲能系統、風電機組和光伏陣列通過不同的變流器接入到交流母線上。用戶負荷由可時移負荷和剛性負荷組成。微電網結構如圖1所示。

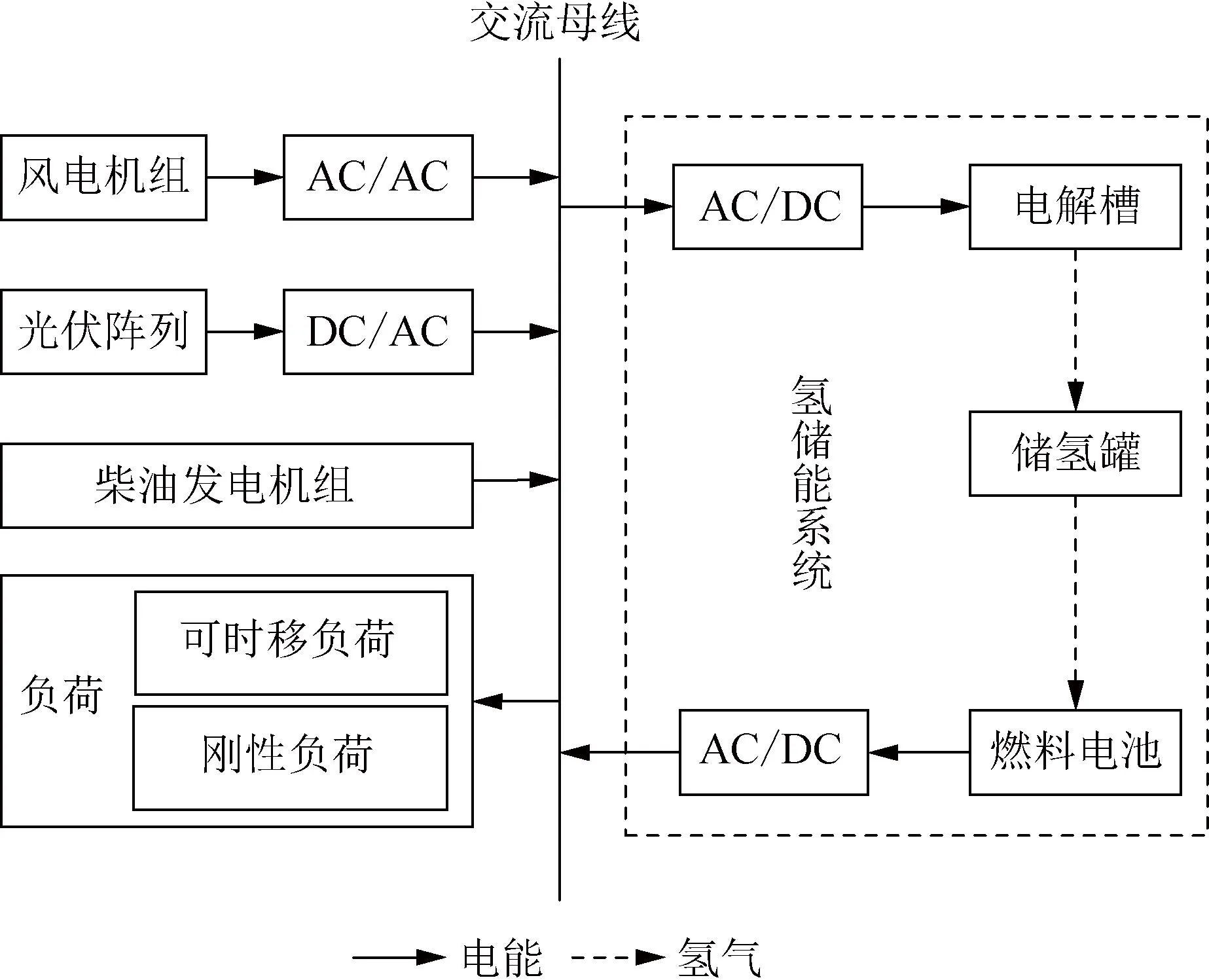
圖1 獨立微電網結構

1.2 氫儲能系統的運行原理及簡化數學模型

微電網內的柴油機發電機組、風電機組和光伏陣列的簡化數學模型參照文獻[28]建立的模型,此處不再贅述。

本文所建電解槽-儲氫罐-燃料電池模型與電池儲能的原理相同。當風光發電功率超過負荷需求時,利用電解槽將剩余電能用于電解水,將產生的氫氣儲存在儲氫罐中,增加了電負荷,提升可再生能源的利用率。在風光發電功率不足以滿足負荷需求的情況下,燃料電池利用儲氫罐中的氫氣作為燃料發電,產生電能以滿足負荷需求,大大增強了系統的可靠性。

1)電解槽數學模型。

常采用堿式電解槽,將水電解產生氫氣和氧氣。其輸出功率為:

Pel,out=ηelPel,in

(1)

式中:Pel,in為電解槽的輸入功率;Pel,out為電解槽的輸出功率;ηel為電解槽的效率,本文取60%。

電解槽的輸入功率最大值受其容量與儲氫罐剩余儲能容量的限制。電解槽的最大輸入功率為:

(2)

(3)

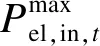
2)燃料電池數學模型。

燃料電池通過燃燒氫氣和氧氣釋放能量。其輸出功率為:

Pfc,out=ηfcPfc,in

(4)

式中:Pfc,out為燃料電池的輸出功率;Pfc,in為燃料電池的輸入功率;ηfc為燃料電池的工作效率,本文取65%。

燃料電池的最大輸出功率也受其容量與儲氫罐剩余容量的限制,可用式(5)、(6)表示。

(5)

(6)

3)儲氫罐數學模型。

儲氫罐既可以存儲電解槽產生的氫氣,又可以為燃料電池提供氫氣。其數學模型為:

(7)

式中:ηtank為儲氫罐的工作效率,本文取為50%。

2 基于IGDT的獨立微電網運行場景構建

為應對風光出力的隨機性和間歇性,本文采用IGDT來模擬風光出力波動幅度的不確定性,其目的為在滿足預設目標的前提下,研究不確定參數對微電網的影響,量化不確定參數的預測值和實際值之間的誤差[29]。其包括風險規避魯棒模型和風險投機機會模型2種,本文考慮IGDT魯棒模型,減少風光出力不確定性的不利影響。

2.1 不確定集構建

首先,IGDT的典型模型[30]為:

(8)

式中:Y為不確定參數;y為決策變量;F(Y,y)為目標函數;H(Y,y)、G(Y,y)分別為等式約束和不等式約束。

在IGDT中,采用包絡邊界不確定性模型[31]進行建模,其表達式為:

(9)

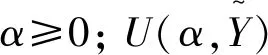
2.2 獨立微電網運行場景構建

當有不確定因素時,保守的決策者為了能實現某一最低目標,將最大化不確定參數的不利擾動,可建立具體模型為:

(10)

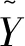
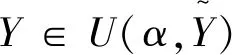
本文不確定參數為風電和光伏兩者的出力,其波動范圍為:

(11)

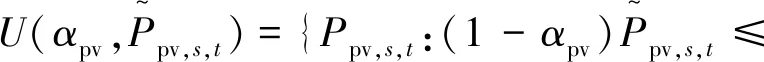
(12)

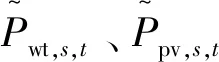
在風光的實際出力小于預測值的環境下,柴油機組和氫儲能系統將承擔系統的功率缺額。但系統的發電總成本勢必將會隨之增加,且功率缺額越多,發電總成本增加越大。因此,當風光的實際出力遠小于預測值時,系統運行成本最大。其取值為:

(13)

(14)

傳統的IGDT方法只適用于單因素參數不確定性。本文同時考慮了風光兩者的不確定性。為消除兩者權重帶來的主觀性,本文提出采用熵權法[32-33]來計算兩者的權重,對其不確定性因素進行重要性評價。其數學表達式為:

(15)

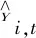
將各不確定變量看作是系統不確定性的指標,使用風光的預測值計算相應的熵權。根據熵權,計算出相應不確定變量在總不確定度中所占的比例:

(16)

3 計及IGDT的獨立微電網雙層魯棒優化規劃模型

本文構建的雙層優化規劃模型中,外層優化模型負責求解長時間尺度的規劃問題,以微電網綜合成本等年值最小為目標;內層優化模型負責短時間尺度的運行問題,以微電網年運行成本最低為目標。內外雙層相互迭代獲得最優規劃結果。

3.1 外層優化模型

3.1.1 目標函數

外層以微電網的綜合成本等年值Z最低為目標。外層優化的決策變量集合x為燃料電池、電解槽、儲氫罐和光伏陣列、風電機組的額定容量。在確定性場景中,外層預期目標成本函數為:

(17)

式中:Zinv為設備投資成本等年值;Zope為系統年運行成本。

由2.2節得,當風光出力朝不利方向發展時,引入IGDT后,微電網決策者所能接受的最大悲觀運行成本和總成本可改寫為:

Z′ope=(1+μ)Zope

(18)

(19)

式中:Z′ope為決策者可接受的最大悲觀運行成本;Z′為微電網綜合成本等年值。

Zinv主要包括各設備的年平均投資成本和年維護成本,計算公式為:

(20)

(21)

式中:k為設備類型,k=1,2,…,5分別表示風電機組、光伏陣列、電解槽、燃料電池和儲氫罐;R為等年值算子;L為系統運行年限;Zf,k第k類設備的單位容量初始投資成本;Zm,k為設備的年維護成本;εk為設備的安裝數量或容量;λ為貼現率。

3.1.2 外層優化模型約束條件

受場地建設面積影響,各類設備投建容量的不等式約束為:

(22)

式中:Cde,N、Cwt,N、Cpv,N分別為柴油機組、風電機組和光伏陣列的額定裝機容量;上標min和max代表最小值和最大值。

3.2 內層優化模型

3.2.1 目標函數

當外層將決策變量x傳遞給內層后,內層以考慮風光出力不確定性的運行場景下系統年運行成本最低為目標進行優化,年運行成本包括燃料成本和DR補償成本。內層的決策變量為一年各時段風電機組、光伏陣列、柴油發電機組和氫儲能系統的充放電功率。內層優化模型為:

Z′ope=min(Zfuel+Zdr)

(23)

式中:Zdr為年負荷轉移補償成本;Zfuel為柴油機組全年燃料成本。

因太陽輻照強度、風速和負荷具有季節性的特點,本文將全年氣象數據和負荷數據分為3類,包括夏季60天、冬季120天、春秋季185天,每類可用一個典型日代表,利用k-means聚類算法得到夏、冬、春秋季典型日的風速、太陽輻照強度和負荷曲線來代替該季節下各天的風速、太陽輻照強度和負荷數據。由此,式(23)可改寫為:

(24)

式中:S為一年中的典型日個數,s=1,2,…,S;ns為一年中第s個典型日的天數;Zdr,s和Zfuel,s為第s個典型日的負荷轉移補償成本和柴油機組燃料成本。

1)柴油發電機組燃料成本。

(25)

(26)

2)激勵型DR成本。

對于獨立微電網而言,其不與大電網相連,主要用于偏遠地區供電,建設成本較高。本文引入激勵型DR,以各時刻的可再生能源發電量和負荷需求兩者的差值絕對值之和最小作為激勵型DR的優化目標,通過調整用戶可轉移負荷的用電時間,使運行周期內的新能源出力曲線和負荷曲線在時序上更貼近,從而促進可再生能源消納,提高微電網的經濟性。激勵型DR表達式為:

(27)

式中:Ppv,s,t、Pwt,s,t分別為第s個典型日t時刻光伏陣列、風電機組的輸出功率;PL0,s,t、PL1,s,t分別為激勵型DR前、后t時刻的負荷功率;ΔPL,s,t為第s個典型日t時刻的負荷轉移量,大于0為負荷轉入,小于0為負荷轉出。

考慮DR后,成本主要為調整可時移負荷需要給予用戶的補償成本,如式(28)所示。

(28)

式中:Cdr為單位電量負荷的轉移補償成本。

3.2.2 內層優化模型約束條件

1)功率平衡約束。

系統功率平衡約束為:

Pel,in,s,t+PL1,s,t=Ppv,s,t+Pwt,s,t+Pde,s,t+Pfc,out,s,t

(29)

2)分布式電源出力約束。

柴油發電機組、風電機組和光伏陣列滿足的約束條件為:

(30)

3)氫儲能系統約束。

儲氫罐、燃料電池和電解槽的功率上下限約束如式(31)、(32)、(33)所示;儲氫罐的荷電狀態上下限約束如式(34)所示;儲氫罐的荷電狀態在一個運行周期內始末相等,如式(35)所示。

(31)

(32)

(33)

(34)

SSOC,tank,t0=SSOC,tank,tN

(35)

式中:SSOC,tank,s,t為典型日s內t時段儲氫罐的荷電狀態;SSOC,tank,t0、SSOC,tank,tN分別為一個運行周期內始末的儲氫罐荷電狀態;t0和tN分別為運行周期的始末時段。

4)柴油發電機組發電量占比約束。

對于獨立微電網,國家規定柴油發電機組發電量占比不應超過20%[34],如式(36)所示。

(36)

5)負荷轉移約束。

負荷轉出或轉入只能在同一個運行周期內,即轉移時段應滿足:

(37)

式中:t0為負荷轉入時段;t1為負荷轉出時段;Tn為第n個運行周期。

各個時刻的負荷轉移量不能超過最大負荷轉移量,且應滿足一個運行周期內DR前、后總負荷需求不變,如式(38)所示。

(38)

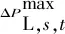
綜上所述,可得計及IGDT的獨立微電網雙層優化規劃模型為:

(39)

3.3 雙層優化規劃模型求解

本文的外層優化模型采用帶有精英保留策略的遺傳算法[35-36]進行求解,在外層模型中遺傳算法的染色體可以精準對各設備容量編碼;內層模型屬于多約束線性模型,可通過Cplex求解器實現高效求解。求解流程如圖2所示。

4 算例分析

本文選取某地區一年的氣象及負荷數據來驗證本文模型的正確性。該地區所用的風光和負荷的小時級數據均為實際測量數據,全年風速、太陽光照強度和負荷隨時間變化的曲線見附錄圖A1。通過k-means算法聚類得到的春秋、夏和冬不同季節段典型日的風速、太陽輻照強度和負荷曲線分別見附錄圖A2。

4.1 方案設置

為驗證本文所提模型的優越性,考慮以下5種方案進行比較:

方案1：不考慮風光出力不確定性和激勵型DR。

方案2：考慮風光出力的不確定性,不考慮激勵型DR。

方案3：根據方案2獲得的容量配置結果在風光出力不確定性場景下的一個應用,為對比說明,將此應用場景設置為方案3。

方案4：在方案2容量配置的基礎上考慮激勵型DR計算最優運行成本。

方案5：同時考慮風光出力的不確定性和激勵型DR計算最優容量配置和運行成本,即本文所提方法。

4.2 方案結果對比

經計算得到的5種方案下微電網的容量配置和成本計算結果對比如表1所示。其中預期目標成本值Z和最大悲觀成本Z′均為等年值。

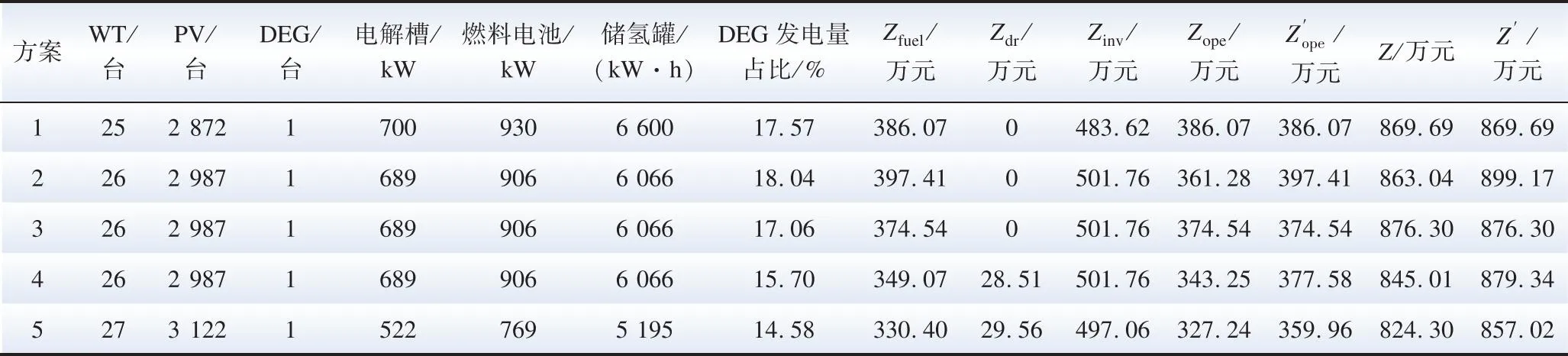
表1 不同方案的容量配置和成本計算結果

4.2.1 風光不確定性對容量配置和成本的影響分析

1)方案1和方案2對比分析。

對比方案1和方案2,可以發現方案2考慮不確定性后的最大悲觀成本比方案1多了29.48萬元。

這是因為在方案1確定性場景下,微電網按照風光預測值進行規劃投資,即風險規避系數和不確定參數均為0。方案2引入IGDT模擬風光不確定性后,計算得到不確定參數α為9.43%,可以理解為生成的規劃方案在規劃期內能夠承受的風光最大波動范圍是9.43%,即系統承受風光不確定性的魯棒性水平是9.43%。此時,微電網決策者要承擔規避系數為10%的投資預算。

2)方案2和方案3對比分析。

根據方案2的計算結果,方案3取α為4%。由表1可知,在相同的容量配置結果下,一方面方案3的總成本Z比方案2在確定性場景下的預期目標成本值Z增加13.26萬元,這是因為在不確定環境中,風光出力會朝著不利的方向發展,為了滿足微電網的功率缺額,必須增加柴油發電機的出力,結果導致了微電網的運行成本大幅增加。另一方面,方案3比方案2的最大悲觀成本Z′少22.87萬元,這是因為風光在一定范圍內任意波動時,所得的魯棒解均能滿足決策者能夠接受的最大悲觀成本,表明決策解具有良好的適應性。

以夏季典型日為例,將方案2在確定性場景下運行情況與方案3運行情況作對比,如圖3、4所示。

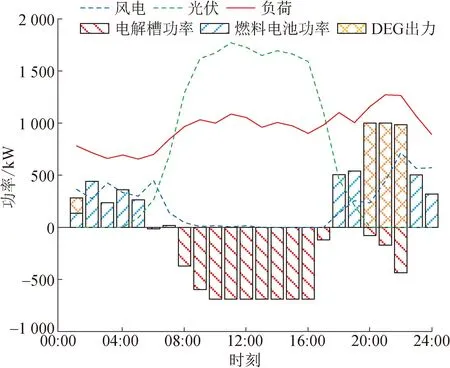
圖3 方案2在夏季典型日確定性場景下微電網的運行結果

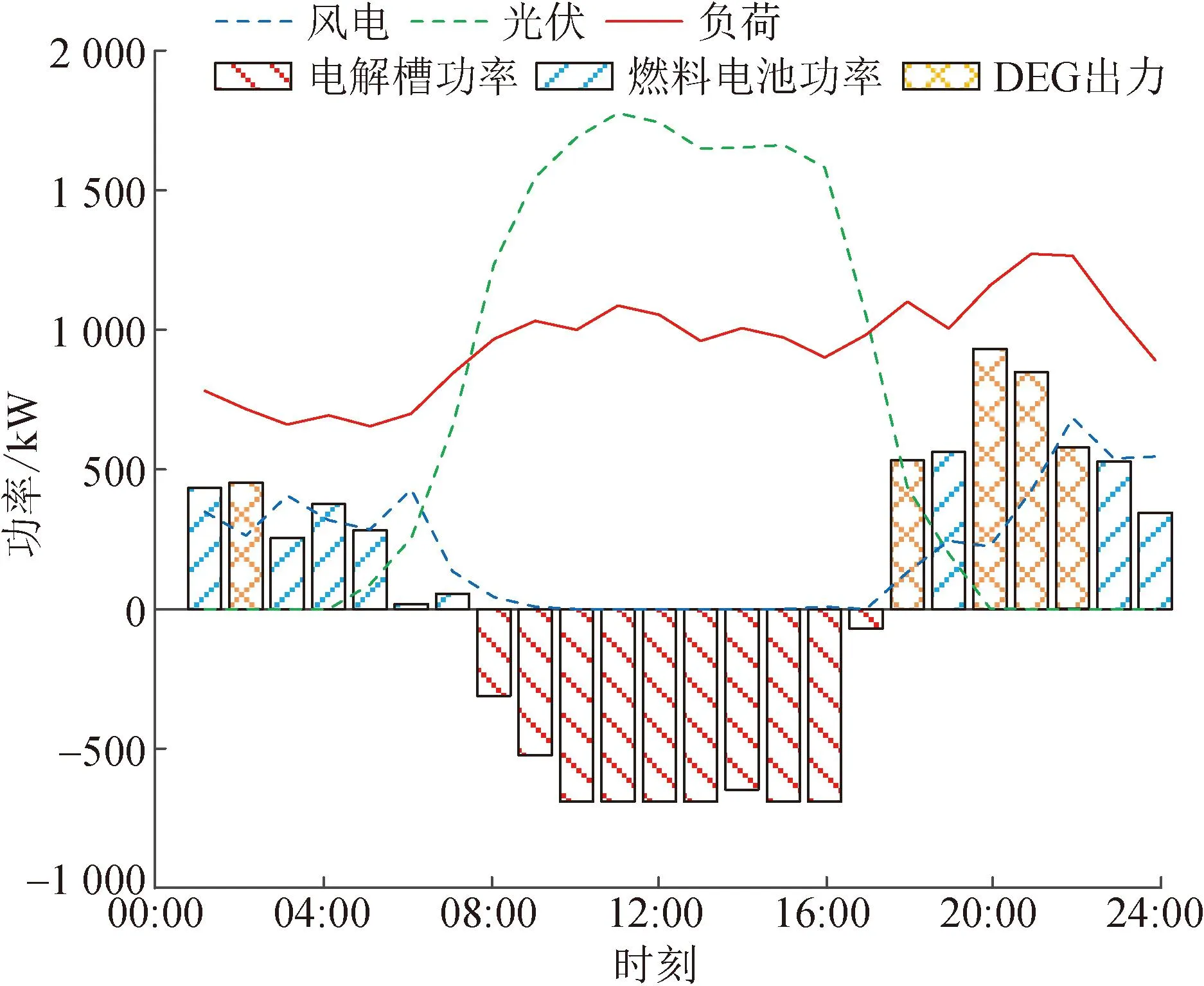
圖4 方案3在夏季典型日不確定性場景下微電網的運行結果

可以發現,在夏季典型日下,方案3為應對風光出力不確定性,柴油發電機的啟用時段比方案2增加了一個,從而導致運行成本升高。

4.2.2 激勵型DR對容量配置和成本的影響分析

1)方案2與方案4對比分析。

由表1可知,對比于方案2,方案4引入了激勵型DR后,柴油機組發電量占比降低2.34%,微電網年運行成本降低19.83萬元,總成本降低了19.83萬元。

2)方案4和方案5的對比分析。

方案5對比于方案4,在容量配置方面風機和光伏裝機容量分別增加了100、135 kW;同時方案5的電解槽、燃料電池和儲氫罐的容量分別降低了167 kW、137 kW和871 kW·h;在運行方面,柴油機組的發電量占比降低了1.12%,柴油費用減少了18.67萬元,投資成本等年值降低了4.7萬元,年運行成本降低了17.62萬元,降低了4.67%,在總成本上降低了22.32萬元。

經分析得知,引入激勵型DR會減少微電網儲能的容量配置,增加風光可再生能源的裝機容量,提高經濟效益。這是因為通過調整可時移負荷的工作時間段,使負荷曲線和風光出力曲線更加一致,提高了可再生能源利用率,減少了平抑風光出力波動所需的氫儲能系統出力和柴油發電機出力。以激勵型DR發揮作用明顯的冬季典型日為例,2種方案下冬季典型日的運行結果分別如圖5、6所示。

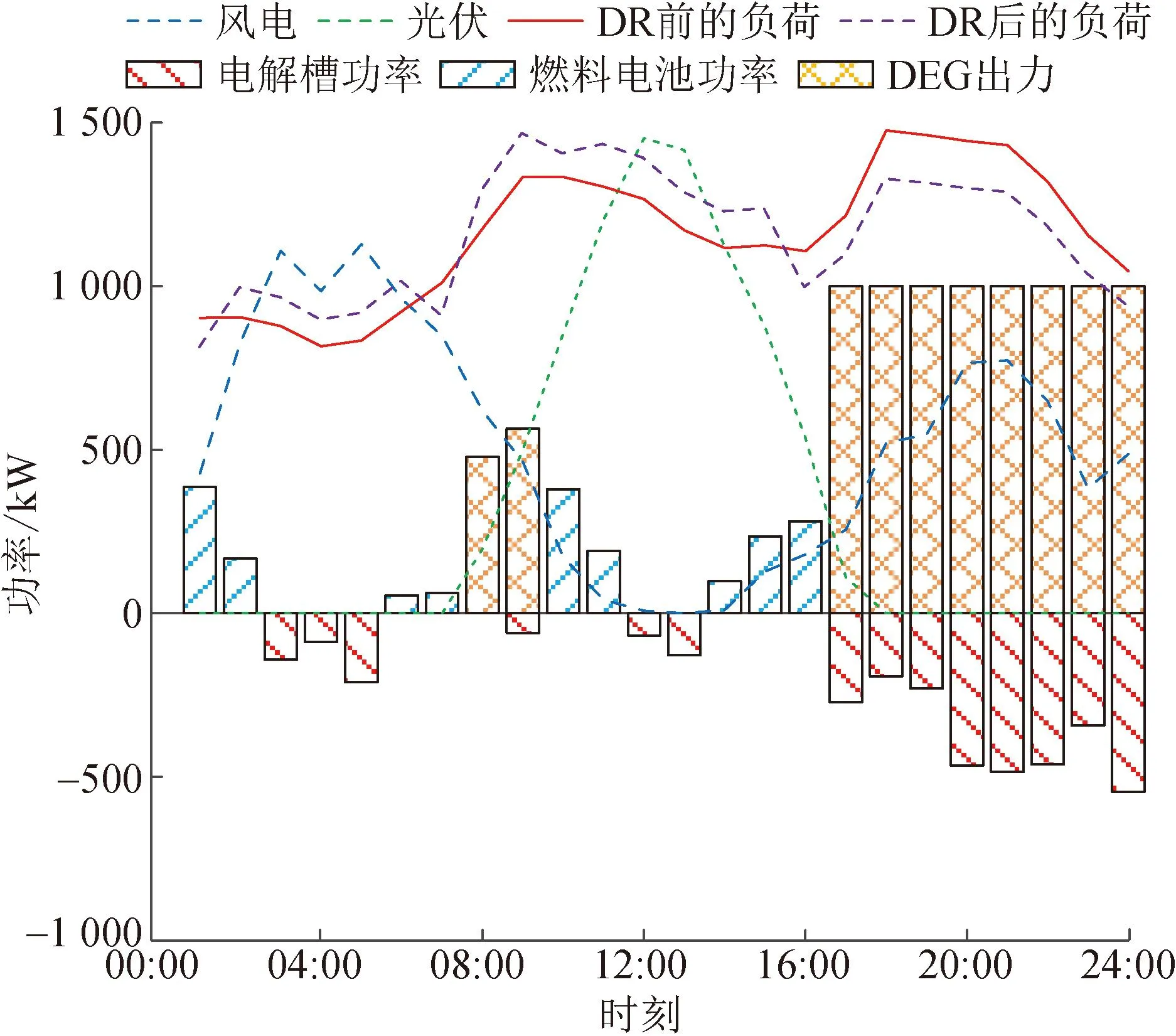
圖5 方案4冬季典型日微電網的運行結果

分析圖5和圖6,在方案5考慮激勵型DR的冬季典型日內的運行結果中,柴油發電機組在啟用的時段個數比方案4減少了1個,從而降低了微電網的運行成本。

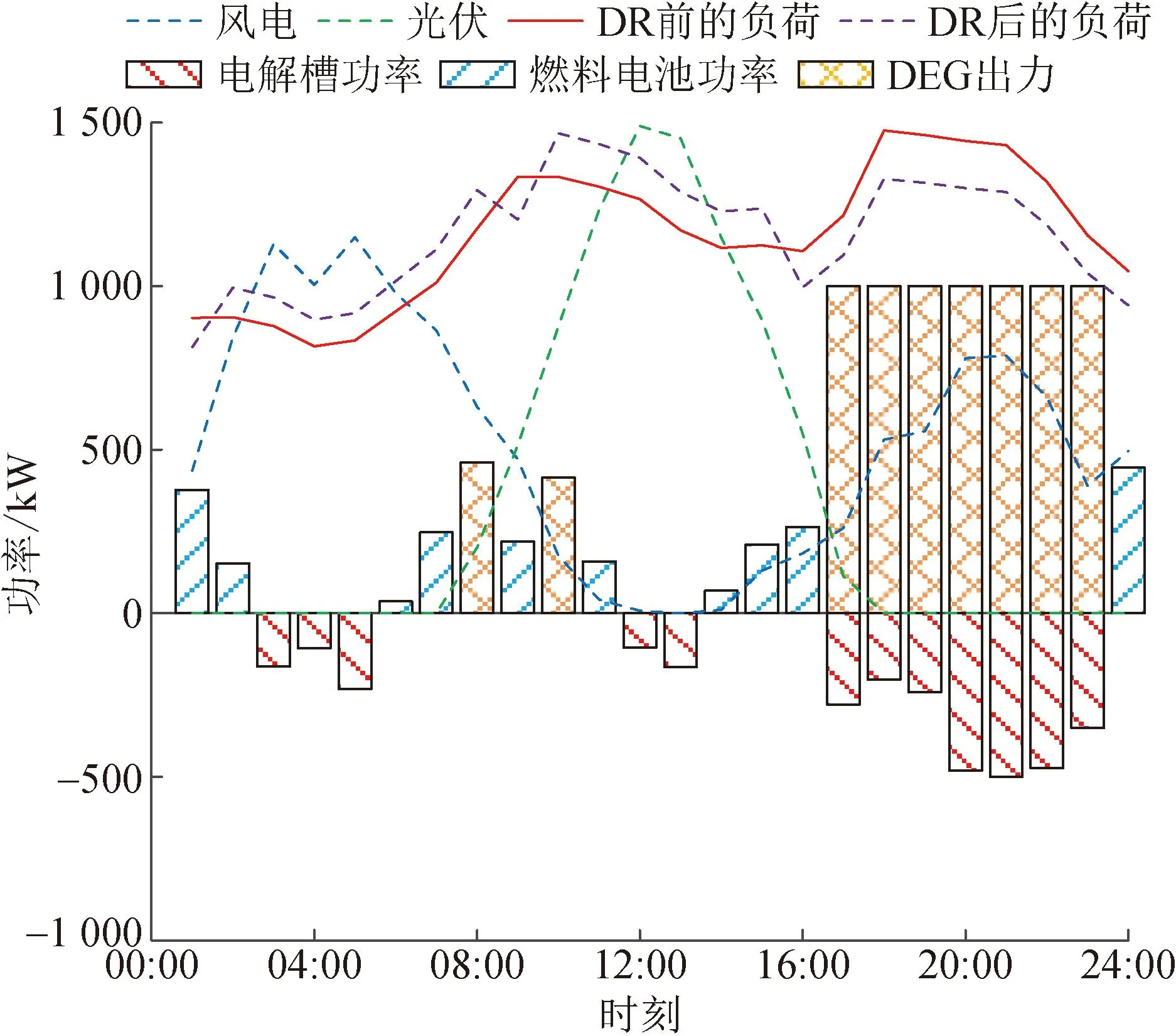
圖6 方案5冬季典型日微電網的運行結果

綜上說明,微電網決策者在規劃時就將激勵型DR考慮在內比在系統建成后施行激勵型DR得到的規劃方案更優。

圖7為方案5在帶精英保留策略的遺傳算法和傳統遺傳算法下的迭代收斂曲線,可以看出,本文采用的遺傳算法收斂速度更快,可以抑制早熟現象,避免了算法陷入局部最優解。

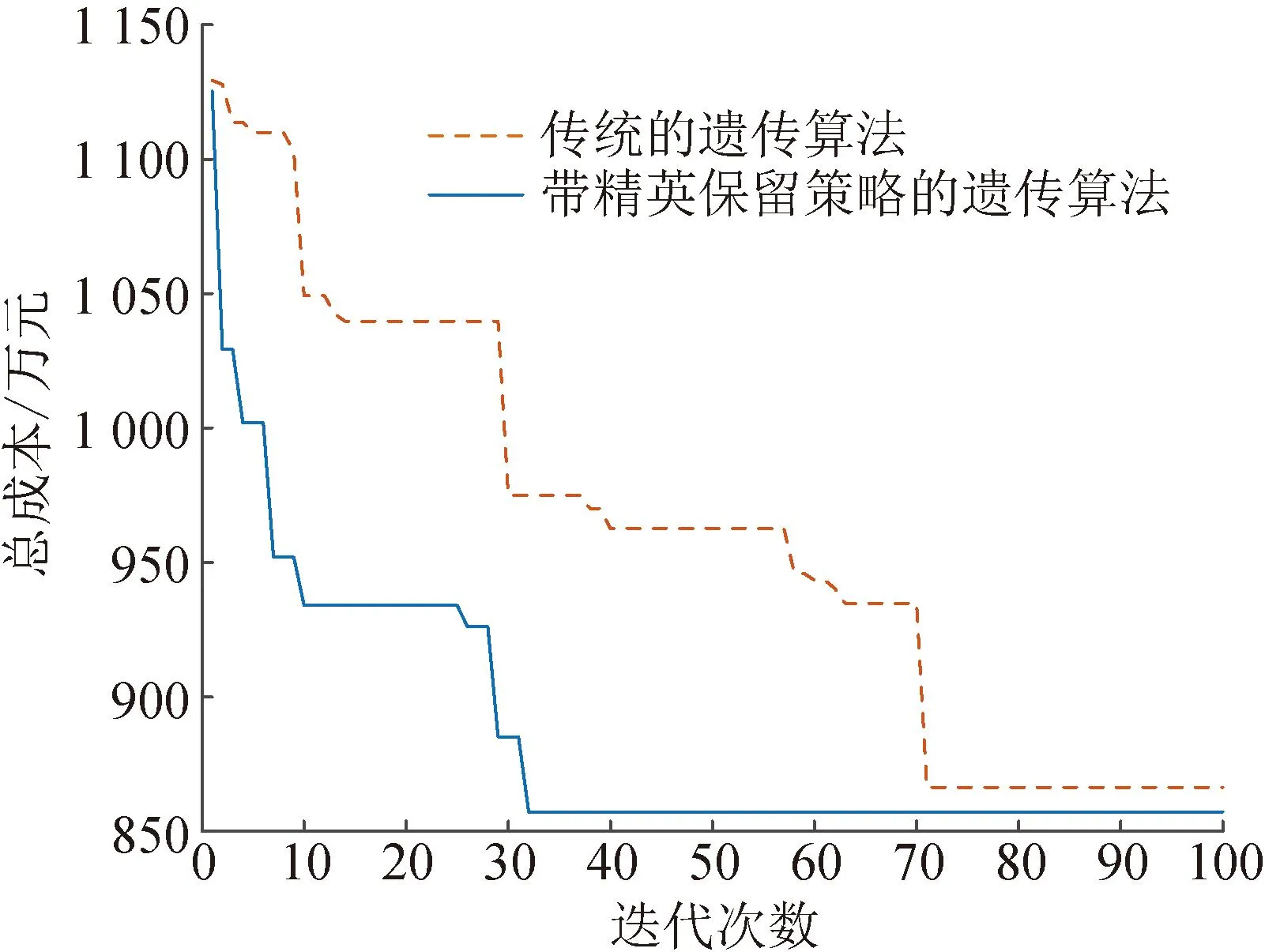
圖7 方案5的迭代收斂曲線

4.2.3 風險規避系數μ的靈敏度分析

為研究不同風險規避系數μ的影響,以方案5為例,設置μ變化范圍為2%～20%。通過計算決策者所能接受的最大悲觀運行成本Z′ope,計算出不確定參數α與運行成本隨μ的變化趨勢,如圖8所示。

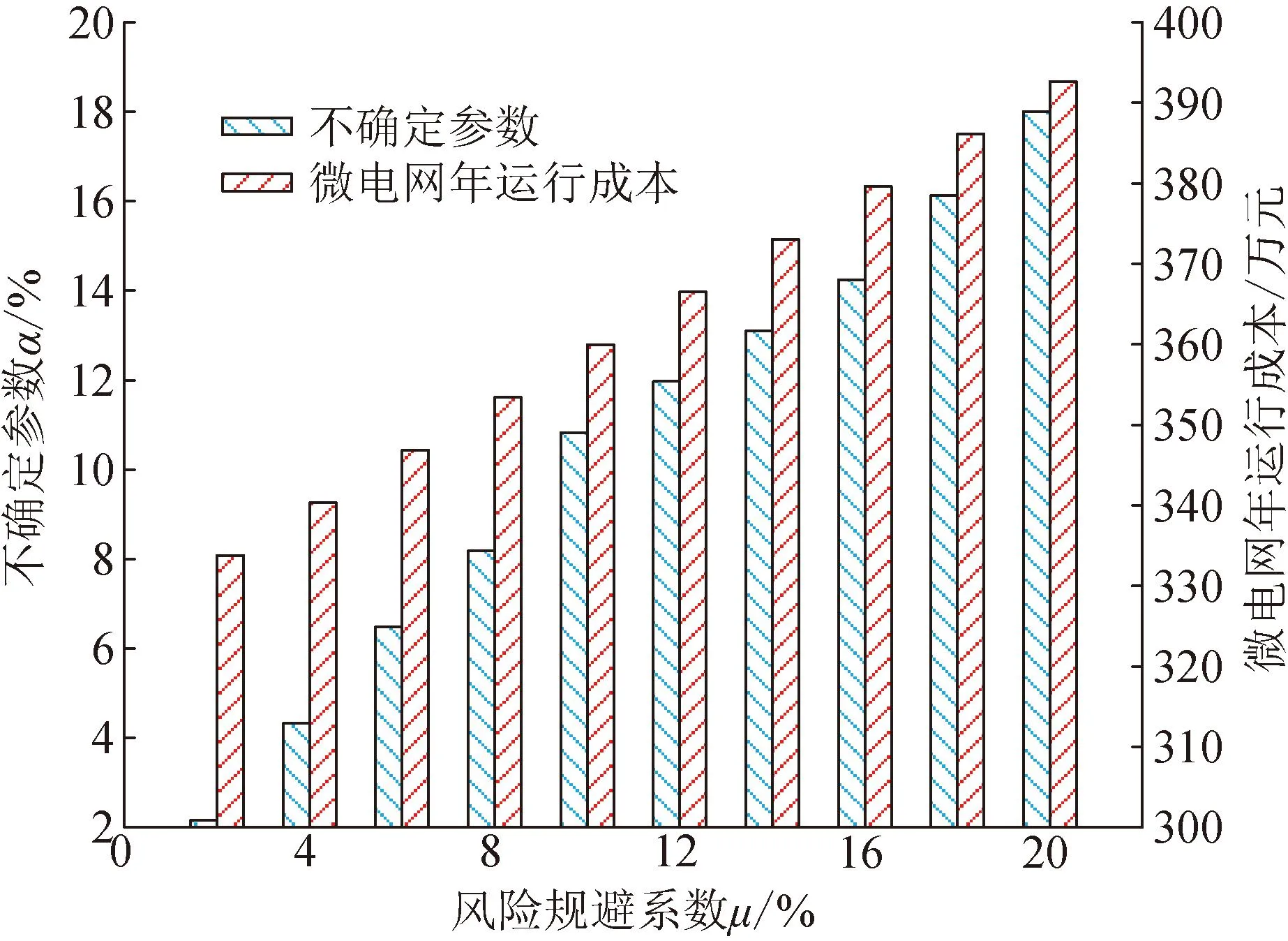
圖8 不同μ對α及微電網年運行成本的影響

由圖可知,隨著μ從2%增加至20%,保守型決策者認為,由于不確定性可能會使目標朝著不利的方向發展,因此他們希望通過增加運行成本來抵抗可能存在的不確定性,以盡可能減少不利影響。當微電網年運行成本由333.78萬元增加到392.69萬元時,微電網可以容納的α從2.16%增加到18.01%。對應地,當風電和光伏出力在波動范圍內變化時,可以確保系統的運行成本低于最大悲觀運行成本。

4.2.4 IGDT魯棒模型的有效性分析

為驗證本文所提IGDT魯棒模型的有效性,在2.2節所建立的不確定集中采用蒙特卡洛模擬技術分別抽取1 000個隨機風電和光伏出力場景,將以上風電和光伏場景逐一代入模型式(39)中檢驗并求取對應場景下的微電網年運行成本。取μ為20%,對應最大悲觀成本為392.69萬元。結果分布如圖9所示。

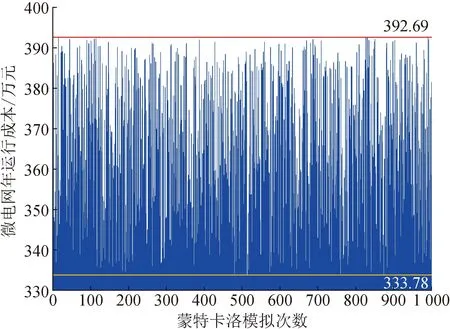
圖9 不確定場景下微電網年運行成本

由圖9可知,在波動范圍內任意的風光出力場景都能夠滿足微電網的運行成本在333.78萬元和392.69萬元之間,微電網此時所能承受的最大α為18.01%。驗證了本文所提模型的有效性。

4.2.5 不同儲能方案下的配置結果分析

為充分分析氫儲能系統相比較于電化學儲能的經濟優勢,選擇目前應用范圍最廣的鋰離子電池作為系統儲能方案,不考慮風光不確定性和激勵型DR。其容量配置和成本計算結果如表2所示。

表2 鋰離子電池儲能的容量配置和成本計算結果

對比表1中的方案1,可以發現:雖然采用氫儲能時,需要配置的儲能容量比采用鋰離子電池儲能高出2 220 kW·h,但氫儲能方案仍比鋰離子電池儲能方案總成本降低72.51萬元。這是因為氫儲能具有能量密度大、容量大的特點,其單位容量成本遠低于鋰離子電池,且氫氣可以長期儲存在適當的條件下而不損失能量,氫儲能壽命也長于鋰離子電池儲能,在長期調節能力方面的貢獻更顯著。

5 結 論

本文提出了一種含氫儲能的獨立微電網IGDT魯棒規劃方法,其具有以下特點:

1)采用IGDT來模擬風光出力不確定性,將其變化幅度與運行成本定量結合,使規劃決策者能夠根據可承受的成本來選擇風險規避系數,得到兼顧經濟性和魯棒性的最優化規劃方案。

2)在構建獨立微電網的優化規劃模型過程中,計入了激勵型DR作用對規劃結果的影響,能夠實現對負荷側資源的充分利用,提高可再生能源的裝機占比,減少氫儲能的容量配置,降低微電網的運行成本,使規劃方案更加合理。