臥式套管潛熱蓄熱單元偏心與肋片結(jié)構(gòu)優(yōu)化模擬

張璐荻，周國兵

（華北電力大學能源動力與機械工程學院，北京 102206）

我國能源行業(yè)在國家“雙碳”目標指引下大力加強可再生能源利用[1]。以太陽能為代表的可再生能源具有安全清潔、總量大和分布廣等諸多優(yōu)點，但同時也存在分散性、間歇性和不穩(wěn)定性等諸多問題，使得能源利用的供需側(cè)存在時間、空間上不匹配的矛盾，這些問題凸顯了發(fā)展熱能儲存技術(shù)的必要性。熱能的儲存可分為顯熱、潛熱和化學熱儲存三種形式。其中，潛熱蓄能，又稱為相變蓄能，主要是利用相變材料(phase change material，PCM)在物態(tài)變化時所釋放或吸收的大量潛熱，具有蓄熱密度高(為顯熱蓄能的5～10 倍[2])、蓄/釋熱溫度穩(wěn)定、易控制等優(yōu)勢[3]，但除金屬/合金類PCM 外，大多數(shù)PCM 的熱導率均較低，難以滿足工業(yè)應用中對蓄放熱速率的需求，已成為制約相變蓄能系統(tǒng)廣泛應用的主要瓶頸之一。因此，強化傳熱技術(shù)一直以來都是相變蓄能領(lǐng)域的研究重點之一，目前著眼于PCM 本身和相變蓄能系統(tǒng)兩個方面，包括提高系統(tǒng)傳熱系數(shù)、增大傳熱溫差、擴展接觸面積等。提高蓄熱材料導熱系數(shù)目前主要是通過添加各種填料來實現(xiàn)的，包括金屬或氧化物納米顆粒[4-5]、納米碳材料(石墨烯、碳納米管等)[6]、泡沫金屬和膨脹石墨等多孔介質(zhì)[7]。增大換熱流體(heat transfer fluid，HTF)與PCM 間的換熱溫差可以顯著提高PCM 的蓄放熱效率，還可以利用梯級相變技術(shù)，即將具有不同相變溫度的PCM 按照一定的順序排列布置形成具有一定相變溫度梯度的復合相變蓄熱系統(tǒng)[8]。擴大PCM和換熱器結(jié)構(gòu)之間的接觸面積也是增強傳熱的一種非常有效的方法，包括PCM 封裝[9]、添加肋片等。由于成本低且易于制造，肋片常用于擴展工業(yè)設備中的換熱面積，學者們通過實驗和數(shù)值研究，分析了各種肋片參數(shù)對潛熱蓄能系統(tǒng)的影響，如肋片的形狀、分布、材料和厚度[10-13]。

除了上述方法，增強PCM內(nèi)部的自然對流是提高相變蓄熱系統(tǒng)性能的新思路。通過水平殼管式相變蓄熱系統(tǒng)的結(jié)構(gòu)變化來提高內(nèi)部自然對流強度的一個簡單措施是調(diào)整內(nèi)管相對于外管中心的相對位置，即偏心布置。Yusuf等[14]通過實驗研究了偏心布置對臥式殼管潛熱蓄熱裝置傳熱性能的影響。通過在重力方向上移動內(nèi)管到三個不同位置來改變偏心率，發(fā)現(xiàn)與同心布置相比向下偏心距離為30 mm時，完全熔化時間減少了67%。Yazici 等[15]在保持入口溫度和質(zhì)量流量不變的情況下研究了偏心布置對石蠟凝固的影響，發(fā)現(xiàn)隨著偏心率增加，總凝固時間增加。然而對于不同參數(shù)不同系統(tǒng)設備尺寸，獲得合適的偏心距離頗具挑戰(zhàn)性。Zheng等[16]指出在某些條件下獲得的偏心距可能不適用于其他情況。

本工作通過對臥式套管潛熱蓄熱單元的流場與溫度場分析提出了“偏心面積比”這一新參數(shù)評價偏心布置蓄熱單元的性能，并通過數(shù)值模擬對較佳偏心位置進行預測，此外針對偏心結(jié)合肋片的強化傳熱問題，在預測的較佳偏心位置對不同形式的肋片進行了數(shù)值模擬以分析其性能，為相變蓄熱單元強化傳熱設計提供參考。

1 物理及數(shù)值模型

1.1 物理模型

臥式套管相變蓄熱單元的物理模型如圖1所示。該裝置由外管和內(nèi)管組成，長度l均為500 mm。外管內(nèi)徑D為40 mm，外設保溫層；內(nèi)管內(nèi)徑d為10 mm，管材為銅，管壁厚度δ為1 mm。蓄熱單元的基本結(jié)構(gòu)是同心的，y用于描述內(nèi)管中心相較于基本結(jié)構(gòu)的偏心距離。選擇水作為HTF從內(nèi)管流過，硬脂酸(stearic acid，SA)為PCM 填充在內(nèi)管與外管之間的環(huán)形空間，表1 為SA、水和銅的各項熱物性參數(shù)。

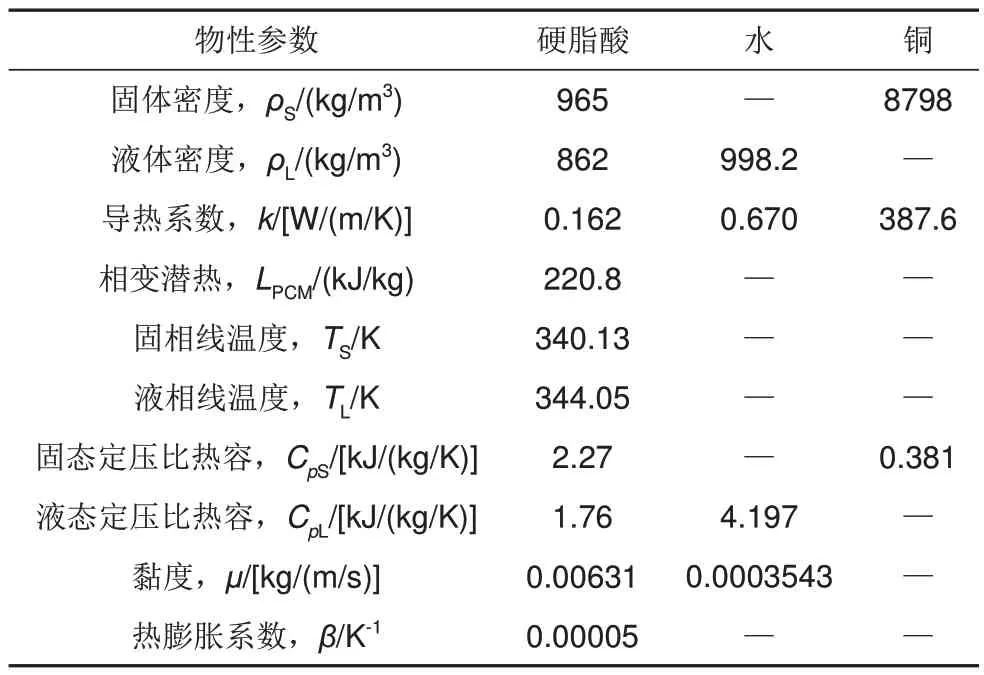
表1 硬脂酸、水和銅的熱物性參數(shù)[2]Table 1 Thermophysical properties of stearic acid,water, and copper[2]

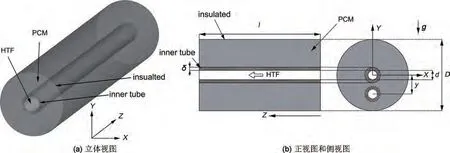
圖1 臥式雙管相變蓄熱單元物理模型Fig.1 Schematic diagram of horizontal double-tube latent heat storage unit

1.2 數(shù)學模型

相變傳熱問題具有很強的非線性，傳熱過程同時存在導熱、自然對流和固液相變。為簡化計算，假設如下：①相變材料在蓄熱單元中均勻且各向同性；②PCM 的密度采用Boussinesq 假設，即密度僅在浮升力項中隨溫度變化；③不考慮黏性耗散產(chǎn)生的熱量；④液態(tài)PCM 為不可壓縮牛頓流體；⑤蓄熱單元初始溫度分布均勻，忽略蓄熱單元散熱損失；⑥模型中流動為非穩(wěn)態(tài)不可壓縮流動，采用層流模型。

基于以上假設，建立潛熱蓄熱單元傳熱過程數(shù)學模型。采用焓-孔隙率法對PCM熔化和凝固進行求解，其中兩相混合區(qū)(糊相區(qū))視為多孔介質(zhì)。當PCM熔化時，多孔介質(zhì)的孔隙率從0增加到1；當PCM 凝固時，孔隙率從1 降低到0。控制方程如下[13,17]：

連續(xù)性方程：

式中，t為時間，s；ρ為密度，kg/m3；p為壓強，Pa；μ為動力黏度，kg/(m/s)；β為熱膨脹系數(shù)，K-1；g為重力加速度，m/s2；T為溫度，K；Tref為參考溫度，根據(jù)Boussinesq 假設，該值假定為PCM的固相線溫度，K；源項S為達西定律阻尼項：

式中，Amush為糊相區(qū)常數(shù)并取值105用于計算[17]，b是小于0.0001 的常數(shù)，以免分母為零，f為液相率，表示為：

式中，hlat為潛熱焓，kJ/kg；L為熔化潛熱，kJ/kg；TS和TL分別為PCM的固相線溫度和液相線溫度，K。

能量方程：

式中，k為導熱系數(shù)，W/(m/K)；Cp為比熱容，kJ/(kg·K)；PCM 總焓htot包括顯熱焓hsens和潛熱焓h

lat：

式中，Tref是參考溫度，K；href為參考溫度下的焓值，kJ/kg；L為熔化潛熱，kJ/kg。

?效率也用于分析蓄熱單元的性能，其定義為PCM中儲存的?與HTF提供的?之比：

式中，ψ為潛熱蓄熱單元的?效率，Exsto和Exinp分別為PCM 中儲存的?和HTF 提供給蓄能單元的?，kJ。m?HTF為HTF的質(zhì)量流量，kg/s；THTF,in和THTF,out分別為潛熱蓄熱系統(tǒng)入口和出口處的HTF溫度，K；T0為環(huán)境溫度即系統(tǒng)的初始溫度，K；TPCM為PCM的平均溫度，K。

1.3 邊界條件和數(shù)值求解

由于所研究臥式相變蓄熱單元的幾何結(jié)構(gòu)是軸對稱的，為了節(jié)省計算資源，取原始結(jié)構(gòu)的1/2 為計算域，選用多面體網(wǎng)格進行劃分，網(wǎng)格質(zhì)量保證在0.7以上，如圖2所示。

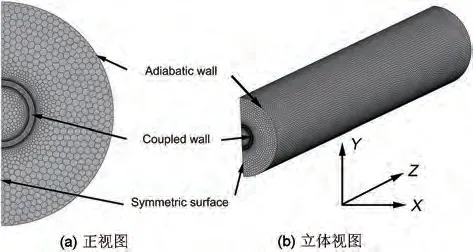
圖2 計算域網(wǎng)格劃分Fig.2 Mesh generated in computational domain

初始時刻PCM的溫度分布均勻，為40 ℃：

HTF入口采用速度入口邊界條件，相應的入口速度(Re=2000)，溫度為：

在HTF 出口處，采用outflow 出口邊界條件，認為出口處流動充分發(fā)展：

內(nèi)管的內(nèi)、外壁面應用耦合邊界條件，外管壁面根據(jù)假設為絕熱邊界條件：

采用基于有限體積法的ANSYS Fluent 軟件對模型進行數(shù)值求解。SIMPLE算法用于求解壓力-速度耦合，PRESTO!方法離散壓力項。能量和動量方程采用二階迎風格式離散。壓力、速度、液相率和能量的亞松弛因子分別設置為0.3、0.7、0.9 和1。連續(xù)性、動量和能量方程的殘差收斂標準分別設置為10-5、10-5和10-6，每個時間步長的最大迭代次數(shù)設置為20。

1.4 無關(guān)性驗證和模型驗證

為了驗證網(wǎng)格和時間步長的獨立性，計算了同心布置中不同網(wǎng)格數(shù)和時間步長的PCM 液體分數(shù)變化，如圖3 所示。圖3(a)表明1.6×105和1.9×105的網(wǎng)格數(shù)之間的液相率最大偏差為9.3%，而1.9×105和2.4×105之間的偏差為1.8%。圖3(b)中，液相率在0.5 s和0.1 s的時間步長之間的最大偏差為13.6%，而在0.1 s 和0.05 s 之間的偏差為3.4%。因此，選取時間步長0.1 s和1.9×105規(guī)格的網(wǎng)格來確保計算的準確性。

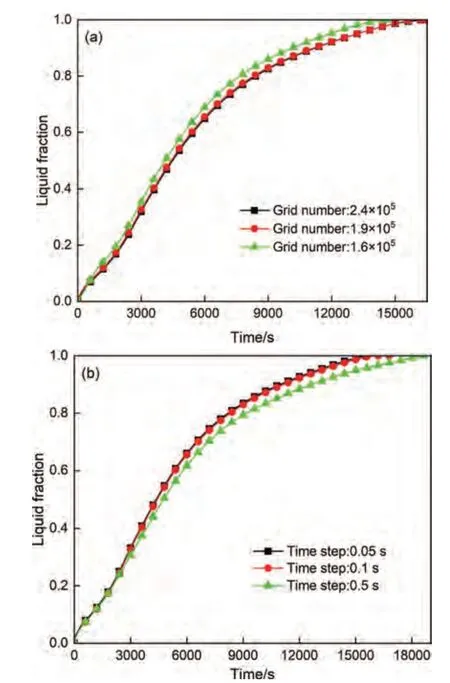
圖3 (a)網(wǎng)格無關(guān)性驗證；(b)時間步長無關(guān)性驗證Fig.3 (a) Grid number independence verification;(b) Time step independence verification

為了驗證當前模型和求解方法的正確性，將上述模型與Hosseini 等[18]的實驗結(jié)果進行對比，如圖4 所示。可見當前模型與Hosseini 等[18]結(jié)果之間PCM 平均溫度最大偏差小于1.4%，表明計算模型是可靠的。

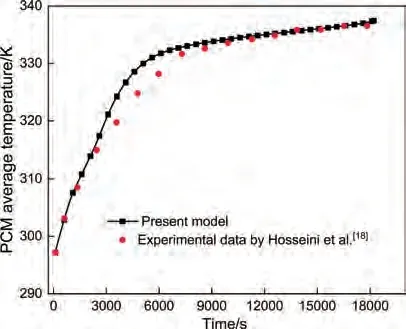
圖4 本文模擬與Hosseini等[18]的實驗結(jié)果比較Fig.4 Comparison between the present model predictions and experimental results of Hosseini et al.[18]

2 結(jié)果與討論

2.1 熔化過程分析和偏心面積比

圖5為臥式套管相變蓄熱單元在長度方向上的中間截面處(z=l/2)的溫度、液相率和流線隨時間變化的分布。在每個截面中，左半部分為熔化過程溫度分布，右半部分為帶有流線的液相率分布。

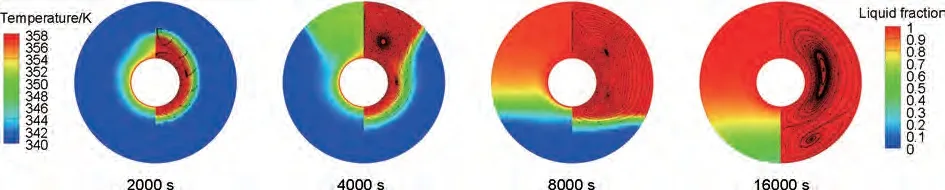
圖5 蓄熱單元中間界面處(z=l/2)隨時間變化的溫度云圖(左)和帶流線分布的液相率云圖(右)Fig.5 Temperature contours (left half) and liquid fraction contours with streamlines (right half) at z = l/2 during the melting of PCM for concentric position

可以看出，在熔化的初期2000 s 左右時液相份額還很少，主要圍繞內(nèi)管壁面呈環(huán)形分布，此階段液相內(nèi)部溫度分布比較均勻，無法產(chǎn)生足夠的密度差，因此在這一時期，自然對流效果很弱，導熱在蓄熱單元的傳熱機理中占據(jù)主導地位。

隨著熔化過程的進行，蓄熱單元內(nèi)部PCM 的液相在單元上部積聚，這主要是因為內(nèi)部液相溫度分布不均勻引起的密度差導致了強烈的自然對流起到了強化傳熱的作用，使得蓄熱單元上部的熔化過程加快。從流線上也可以看出該階段單元上部流動更加劇烈，這時蓄熱單元的傳熱機理為自然對流主導。

隨著自然對流的持續(xù)強化傳熱作用，當熔化時間為8000 s時蓄熱單元的上部區(qū)域已經(jīng)完全熔化，從溫度云圖可以看出此時單元上部液相溫度分布比較均勻，而在單元下部區(qū)域PCM 處于較低溫度，這種向上的溫度梯度使得自然對流效果減弱且很難影響到單元下部區(qū)域。因此單元底部依靠導熱需要更長的時間去完全熔化(16000 s)，此時的傳熱機理又變?yōu)閷嶂鲗В⑶矣捎谙嘧儾牧蠠釋实偷脑蚴沟孟虏繀^(qū)域成為更難熔化的區(qū)域。

因此基于上述分析可以將蓄熱單元內(nèi)部根據(jù)傳熱機理不同劃分為兩個區(qū)域，如圖6所示，即自然對流主導區(qū)域(溫度云圖中紅色部分)，弱自然對流與導熱主導區(qū)域(溫度云圖中分層溫度部分和藍色部分)。

采用偏心布置可以擴大熔化較快的自然對流主導區(qū)域，縮小熔化較慢的弱自然對流與導熱主導區(qū)域面積，進而縮短蓄熱單元整體熔化時間，所以兩個區(qū)域的面積關(guān)系是決定臥式套管偏心相變蓄熱單元的固有因素。在此基礎(chǔ)上提出了一個新的參數(shù)“偏心面積比”來評估偏心蓄熱單元的性能，其定義如下：單元截面圖上自然對流主導區(qū)域面積(A1)和弱自然對流與導熱主導區(qū)域面積(A2)之比，即：

為獲得設計蓄熱單元的較佳偏心面積比利用數(shù)值模擬展開研究。

2.2 蓄熱單元的偏心優(yōu)化

為了獲得偏心面積比和完全熔化時間的關(guān)系，模擬了在不同偏心面積比的熔化過程(Tin=85 ℃，入口Re=2000，win=0.073 m/s)，表2 列出了5 個不同偏心面積比(同心布置和?=4∶1、8∶1、16∶1、24∶1)的偏心距離y。

2.2.1 液相率與熔化云圖

圖7 表示不同偏心面積比的液相率隨時間變化，可以看出不同偏心面積比下的液相率上升呈類似趨勢，與2.1節(jié)分析獲得的熔化過程一致。另外，還發(fā)現(xiàn)完全熔化時間隨著?的增加而不斷減少，當達到16∶1時獲得最短的熔化時間8700 s，相較于同心布置縮短了45.8%。然而當偏心面積比增加到24∶1時，總?cè)刍瘯r間反而會增大到9070 s，這主要是因為偏心過大，下部區(qū)域的導熱主導面積變得非常小，以至于在熔化初期幾乎完全熔化，比上部要早得多，導致上部區(qū)域的熔化負荷比下部區(qū)域的更大，從而整個單元的總?cè)刍瘯r間變得更長。

圖8為不同偏心面積比熔化過程的溫度與液相率云圖，可以看出對于各偏心面積比情形，在熔化初期內(nèi)部的熔化前沿在導熱作用下具有相同趨勢，并且隨著熔化過程進行，在較小偏心面積比情況下，上部自然對流主導域的熔化前沿均比下部導熱區(qū)域先到達蓄熱單元邊界。在較佳偏心?=16∶1處則是上部區(qū)域和下部區(qū)域的熔化前沿同時到達蓄熱單元邊界。當偏心面積比繼續(xù)增加時，可以看到下部區(qū)域的熔化前沿在初期就已經(jīng)到達了單元下邊界，而上部區(qū)域還在向外擴展，這也解釋了為什么偏心過大反而會增加熔化時間。理論上，當自然對流主導區(qū)域的熔化前沿和導熱區(qū)域的熔化前沿同時分別到達蓄熱單元的上、下邊界時即可獲得此時的最佳偏心，這也對偏心面積比這一參數(shù)的合理性給予了證明。但獲得的較佳偏心面積比在16∶1附近是只針對當前使用的材料(SA)獲得，對于其他材料，可以預期最佳偏心面積比與使用材料的自然對流強度和導熱能力之間的比值有直接相關(guān)。

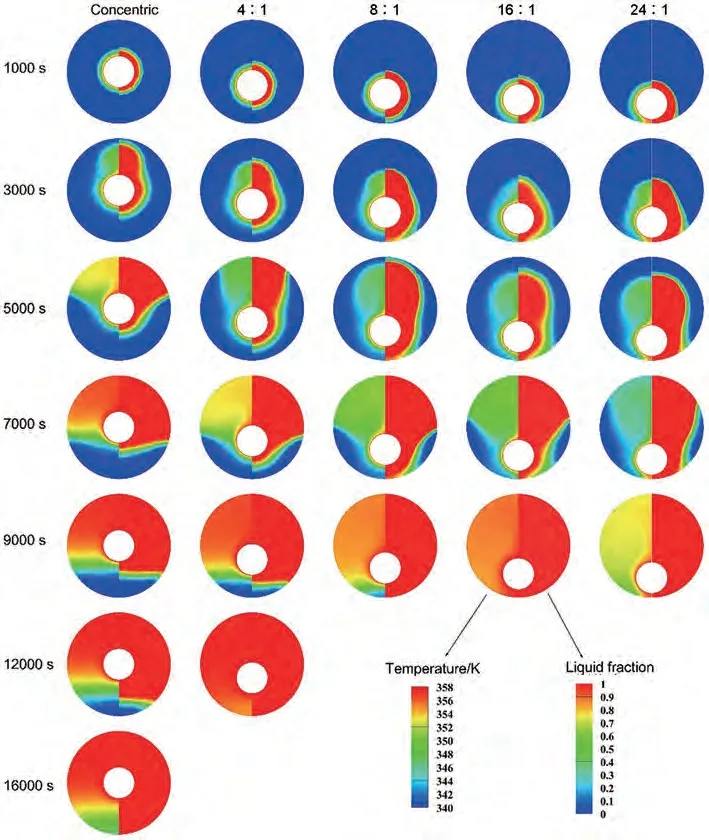
圖8 不同偏心面積比的溫度(左)和液相率(右)云圖(z=l/2)Fig.8 Temperature (left half) and liquid fraction contours (right half) with varying eccentric area ratios

2.2.2 ?效率分析

圖9為不同偏心布置下?效率隨時間變化曲線圖，可以發(fā)現(xiàn)蓄熱單元的?效率都呈現(xiàn)出隨時間增加的趨勢，這是因為隨時間推移，PCM 溫度逐漸升高與HTF 之間的溫差減小，進而?損失逐漸減少，系統(tǒng)的?效率逐漸增加。還可以看到隨偏心面積比的增加?效率呈下降趨勢，這主要是因為隨偏心面積比增大，單元上部自然對流主導區(qū)域面積增加，避免了由于對流強烈而產(chǎn)生的過熱現(xiàn)象，內(nèi)部溫度更加均勻，所以在熔化過程大部分時間里大偏心面積比的平均溫度相對更低，與HTF的溫差相對更大，導致了?損失更大，?效率變低。但由于偏心布置會加快熔化速率，所以在后期大偏心比由于已經(jīng)全部熔化，單元整體溫度高于相變溫度，平均溫度更高，溫差變小，相較于小偏心布置?損失更少，所以在圖9看出在熔化后期不同偏心?效率之間差距縮小，這意味著偏心布置雖然縮短了蓄熱單元的熔化時間，但會使蓄熱單元?效率略有降低。

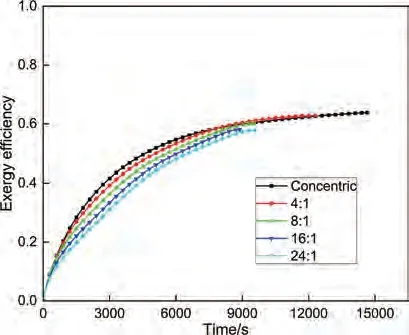
圖9 不同偏心面積比的?效率--時間曲線Fig.9 Time dependent exergy efficiency with varying eccentric area ratios

2.3 偏心布置與肋片結(jié)合

上述分析得到的較佳偏心面積比16∶1相較于同心布置完全熔化時間縮短了45.8%，但從圖8液相率云圖中可以看出在蓄熱單元靠近左右邊界處熔化還是較為緩慢，因此嘗試利用擴展接觸面積與偏心布置相結(jié)合的方式來進一步加速內(nèi)部熔化過程。本工作在?=16∶1的基礎(chǔ)上設計了三種不同的肋片結(jié)構(gòu)，分別為螺旋肋、十字肋和X形肋，其結(jié)構(gòu)和尺寸如圖10 所示，為便于比較，這三種不同形狀的肋片具有相同的體積，沿肋片伸展方向上厚度均為1 mm。

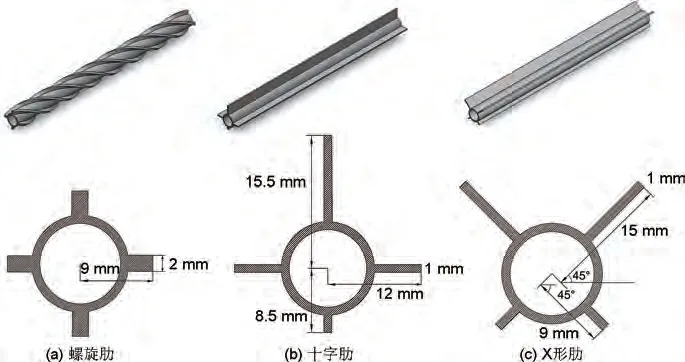
圖10 三種肋片結(jié)構(gòu)及尺寸Fig.10 Structures and sizes of three kinds of fins

圖11 和圖12 分別為三種肋片結(jié)構(gòu)的液相率隨時間變化曲線圖和熔化過程長度方向中間截面處的溫度和液相率云圖。從圖11 可以看出有螺旋肋、十字肋和X形肋的偏心蓄熱單元結(jié)構(gòu)的完全熔化時間分別為6910 s、5930 s 和5510 s，相較于偏心面積比同為16∶1的無肋片基礎(chǔ)結(jié)構(gòu)熔化時間分別縮短了20.6%、31.8%和36.7%。其中螺旋肋片對熔化速率的提升效果較差，這主要是因為螺旋肋相較于其他兩個肋擴展的換熱面積更小，所以初期導熱主導階段液相率上升相對緩慢，從圖12 云圖上也可以看出在自然對流主導的階段其影響并未達到單元左右邊界以加速其熔化。而十字肋和X形肋由于擁有相同的擴展換熱面積，所以在熔化初期導熱主導階段液相率上升具有相近速率，而從云圖上可以看出十字形肋片的上、下肋分別加速了熔化前沿在單元上、下方向的擴展速率，左右肋片也因增加橫向的擴展面積而擴大了上部自然對流的影響范圍，并且可以看出也對較難熔化的單元左右邊界起到一定強化作用。相比之下，X形肋片同時具有增強導熱和自然對流的作用，既利用肋片的結(jié)構(gòu)直接導熱作用擴大傳熱面積加速了單元左右邊界熔化，又因其肋片有一定傾斜角度引導自然對流沿其流動，進而其影響范圍也擴大到了單元左右邊界，所以具有更好的強化傳熱效果。

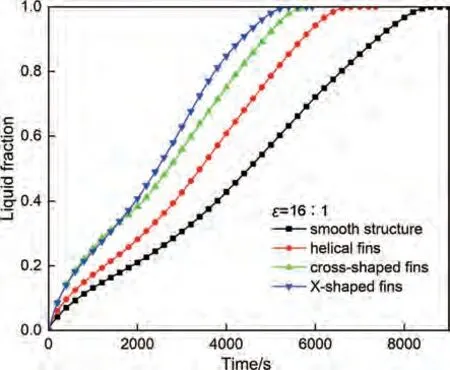
圖11 不同結(jié)構(gòu)肋片與無肋單元的液相率--時間曲線Fig.11 Time dependent liquid fraction with varying fin structures (ε=16∶1)

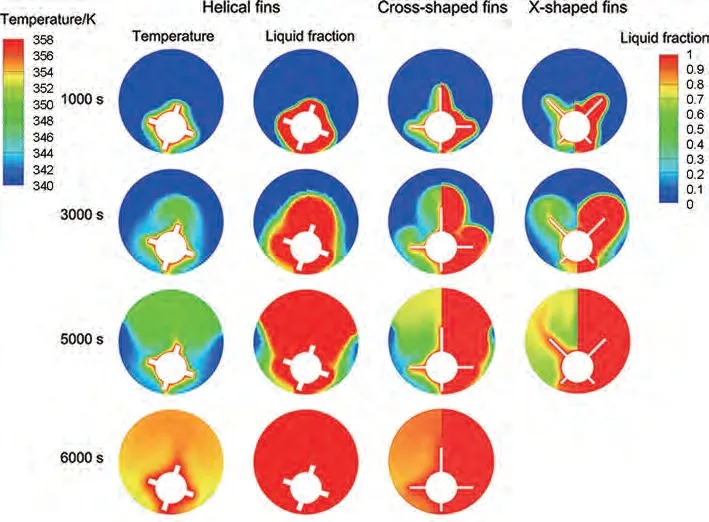
圖12 不同肋片結(jié)構(gòu)的溫度(左)與液相率(右)云圖(z=l/2)Fig.12 Temperature (left half) and liquid fraction contours (right half) with varying fin structures

3 結(jié) 論

本工作建立了臥式套管相變蓄熱單元數(shù)學模型，并對環(huán)形空間內(nèi)PCM 的熔化過程進行數(shù)值模擬，以獲得潛熱蓄熱單元強化傳熱的較佳偏心與肋片結(jié)構(gòu)。相關(guān)結(jié)論如下。

（1）通過對臥式套管相變蓄熱單元熔化過程流場與液相擴展分析，將熔化過程劃分為三個階段：導熱主導的初始階段，隨后是自然對流和導熱的混合作用中間階段，以及導熱再次占主導的最終階段。并據(jù)此將PCM 分布的環(huán)形空間劃分為兩個區(qū)域，進而提出新的評價參數(shù)“偏心面積比”。得出硬脂酸為PCM 時較佳的偏心面積比位于16∶1 附近，熔化時間相對于同心布置縮短了45.8%。

（2）針對偏心潛熱蓄熱單元進行了?效率分析，發(fā)現(xiàn)蓄熱單元的?效率呈現(xiàn)出隨時間增加的趨勢，并且隨著偏心面積比的增加?效率呈下降趨勢，即偏心布置縮短了蓄熱單元的熔化時間，但會使單元的?效率略微降低。

（3）利用偏心布置結(jié)合肋片的方法進一步強化傳熱，設計了螺旋肋、十字肋和X 形肋三種結(jié)構(gòu)，在同為?=16∶1條件下，相較于無肋結(jié)構(gòu)熔化時間分別縮短了20.6%、31.8% 和36.7%，采用偏心結(jié)合X形肋的結(jié)構(gòu)可以獲得較佳性能。

符號說明

Amush—— 糊相區(qū)常數(shù)

A—— 面積，mm2

Cp—— 比熱容，kJ/(kg·K)

D—— 外觀內(nèi)徑，mm

d—— 內(nèi)管內(nèi)徑，mm

EX—— ?，mm

f—— 液相率

g—— 重力加速度，m/s2

h—— 比焓，kJ/kg

k—— 導熱系數(shù)，W/(m·K)

L—— 潛熱，kJ/kg

l—— 長度，mm

m—— 質(zhì)量流量，kg/s

p—— 壓力，Pa

Re—— 雷諾數(shù)，量綱為1

S→—— 源項

T—— 溫度，K

t—— 時間，s

u,v,w——X,Y,Z方向速度，m/s

y—— 偏心距離，mm

希臘字母

ρ—— 密度，kg/m3

μ—— 動力黏度，kg/(m·s)

β—— 熱膨脹系數(shù)，K-1

ψ—— ?效率

δ—— 厚度，mm

?—— 偏心面積比

下標

S—— 固態(tài)

L—— 液態(tài)

PCM—— 相變材料

HTF—— 換熱流體

sens—— 顯熱

lat—— 潛熱

tot—— 總熱

ref—— 參考

sto—— 儲存

inp—— 輸入

in—— 入口

out—— 出口