真題解法引反思 教學勿念囫圇經
——從2023年6月浙江高考實驗試題談起
陳宗濤
(仁懷市第一中學 貴州 遵義 564500)
浙江作為第一批高考改革試點省份,從2014年起采取了一系列改革舉措并不斷優化和完善.筆者作為一線物理教師,持續關注浙江高考改革,尤其對其高考物理試題情有獨鐘.近來,在研究2023年6月浙江省選考物理實驗題時,發現某些資料書上的參考答案和解析值得商榷.就此,筆者試圖從自己的教學經驗出發予以解讀和詮釋,借此與廣大同行分享交流.
1 原題與評析
【原題】如圖1所示,某同學把A、B兩根不同的彈簧串接豎直懸掛,探究 A、B 彈簧彈力與伸長量的關系.在 B 彈簧下端依次掛上質量為m的鉤碼,靜止時指針所指刻度xA、xB的數據如表1所示.

表1 不同重物下A、B彈簧指針刻度

圖1 實驗裝置圖
鉤碼個數為 1 時,彈簧 A 的伸長量ΔxA=________cm,彈簧B的伸長量ΔxB=________cm,A、B兩根彈簧彈性勢能的增加量ΔEp________mg(ΔxA+ΔxB)(填“=”“<”或“>”)
評析:本題以胡克定律的實驗情境為背景,考查學生對彈簧形變量和彈性勢能的理解,與教材不同的是教材中采用單根彈簧的懸掛,本題中采用了彈簧串聯的方式,并且明確指出兩根彈簧是不相同的,這增加了試題的難度.題干利用鐵架臺展現實驗器材,利用表格呈現相關數據,滲透了科學探究的核心素養.本題設問相對簡潔,減輕了學生對高考實驗試題的閱讀壓力,可以緩解學生面對考試的緊張心理.
2 觀點與分析
2.1 資料的觀點
觀點一:
鉤碼個數為1時,由表中數據可知
ΔxA=8.53 cm-7.75 cm=0.78 cm
ΔxB=18.52 cm-16.45 cm-
0.78 cm=1.29 cm
由機械能守恒定律可知,彈簧增加的彈性勢能等于鉤碼減小的重力勢能,故彈簧增加的彈性勢能
ΔEp=mg(ΔxA+ΔxB)
觀點二:
由表中數據可知
ΔxA=8.53 cm-7.75 cm=0.78 cm
ΔxB=18.52 cm-16.45 cm-
0.78 cm=1.29 cm
除了鉤碼的重力勢能減少之外,兩根彈簧的重力勢能也減少,它們都將轉化為彈簧的彈性勢能,因此兩根彈簧增加的彈性勢能大于鉤碼減少的重力勢能,即
ΔEp>mg(ΔxA+ΔxB)
2.2 筆者的觀點
上述觀點一和觀點二對ΔEp的解答中存在一個共同的誤區:從能量的轉化和守恒思想來進行分析,誤認為鉤碼從彈簧原長位置釋放到最終鉤碼靜止不動的過程中,重力勢能與彈性勢能是等量轉化,這個解答沒有考慮到整個過程中除了鉤碼的機械能、彈簧的彈性勢能相互轉化外,應該還有內能參與轉化.理由如下:我們根據豎直彈簧振子模型可以知道,鉤碼從彈簧原長位置靜止自由釋放到鉤碼第一次經過平衡位置(彈力等于重力的位置)時鉤碼必有速度,鉤碼減少的重力勢能有一部分要轉化為鉤碼動能,并沒有全部轉化為彈簧的彈性勢能,并且鉤碼是經過多次上下振動后才能靜止在這個平衡位置,所以整個運動過程中鉤碼和彈簧組成的這個系統機械能并不守恒,而是有內能生成,減少的重力勢能要大于增加的彈性勢能,所以觀點一和觀點二從彈簧與鉤碼組成的系統機械能守恒的角度來分析解答本題是不正確的.
筆者認為根據人教版普通高中課程標準實驗教科書物理必修2第七章第5節“探究彈性勢能的表達式”中的內容,還可找到定量解決這個問題的正確途徑.彈性勢能是狀態量,與發生形變的過程無關,由最終所處的狀態決定.根據功能關系,某狀態下彈性勢能的值等于使彈簧從原長形變到該狀態的過程中克服彈力做的功,我們可以作出彈力F隨形變量l變化的F-l圖像,結合微元思想可知圖像和橫軸所圍的“面積”則為該狀態下彈性勢能的值.此題中我們分別考慮彈簧A和彈簧B,它們的初始狀態都是原長,最終鉤碼處于靜止狀態時兩彈簧的伸長量分別是 ΔxA和 ΔxB且兩彈簧的彈力都等于重力,畫出兩彈簧的F-Δx圖像(圖2),則可根據圖像分別求出彈簧A和彈簧B增加的彈性勢能.

圖2 兩彈簧的F-Δx圖像
彈簧A增加的彈性勢能由圖像可得
彈簧B增加的彈性勢能由圖像可得
所以有A、B彈簧增加的彈性勢能總和
ΔEp=ΔEpA+ΔEpB=
所以本題答案應選“小于”.
3 基于本題引發的思考
3.1 教學中要重視物理觀念的生成過程
人教版普通高中課程標準實驗教科書物理必修2第七章第5節“探究彈性勢能的表達式”中給出了彈性勢能表達式的推導方法,主要運用了類比和微元思想.教學中要逐步分析,不能直接給出結果.建議教學片段如下.
3.1.1 用類比的方法討論彈性勢能
對于彈性勢能表達式的確立,根據功是能量轉化的量度,研究做功對某種能量的影響,從而了解這種能量.類比重力勢能與重力做功的研究過程,我們在研究彈性勢能的表達式時也可以通過彈力做功的特點和功能關系來進行研究.當彈簧沒有發生形變(即原長)時,不存在彈性勢能,當發生彈性形變(被拉長或壓縮)后,彈力做功,即存在彈性勢能.
3.1.2 用微元的思想分析彈力做功
下面以彈簧被拉長為例推導彈性勢能的表達式.小范圍內,重力做功等于重力乘以物體位移的豎直分量.但對于彈力做功情況就要復雜點,重力可看作保持不變,彈力是一個變力.但彈力、伸長量符合正比例函數關系,我們可以借鑒勻變速直線運動位移計算思想,用類似的方法做如下處理.
如圖3所示,將彈簧自A到B的過程分成若干小段,每一個小段為Δl1、Δl2、Δl3、…
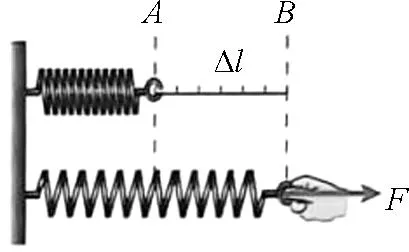
圖3 彈簧拉伸過程
每一個小段中,認為彈力保持不變,依次為F1、F2、F3、…
各小段內克服彈力做的功可分別表示為F1Δl1、F2Δl2、F3Δl3、…
整個過程中克服彈力做的功等于各小段克服彈力做功的代數和,即F1Δl1+F2Δl2+F3Δl3+…
3.1.3 用面積法計算彈力做的總功
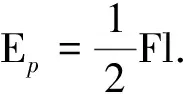
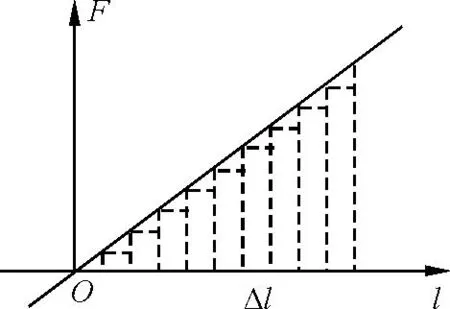
圖4 F-l圖
得出彈性勢能的大小只與彈簧的勁度系數和形變量有關.
3.2 教學中要重視科學推理能力的培養
《普通高中物理課程標準(2017年版2020年修訂)》指出:高中物理要注重體現物理學科的本質,從物理觀念、科學思維、科學探究、科學態度與責任等方面體現物理學科育人價值[2].科學思維作為物理學科核心素養的核心要素,由科學推理與模型構建、科學論證、質疑創新等構成,是高考評價確定學科考查內容的重要依據[3].近年來高考試題普遍關注對學生科學推理能力的考查,2021 年全國甲卷對科學推理能力的考查分值占比高達49.10%[4].而科學推理能力建立在現有信息的分析和提取過程中,這也就是日常教學中常提到的“審題”,對題干中每一句話所代表的含義和給出的信息進行精確的分析和解讀,進而建構模型是正確解題的先決條件,這需要在日常的教學過程中加強學生科學推理、模型建構能力的培養.
3.3 教學中要重視物理思想和方法的滲透
本文中所提到的高考試題是近些年高考改革趨勢,首先設置物理實驗探究情境,將情境中的探究數據、處理結果進行展示,進而對探究過程中的原理、操作方法、數據處理等科學探究核心素養進行考查.這對學生知識的靈活運用、教師的教學提出了新的要求.在日常的教學過程中普遍存在重知識和技能、輕思想和方法的現象.這會造成學生存在知識死記硬背、運用不夠靈活、具體現象不能具體分析等弊端,這些問題歸結在一起就是學生的科學探究能力沒有得到足夠的鍛煉,致使其遇到案例式題目無法做到知識的靈活運用和分析.例如本實驗考查的彈性勢能,雖高中階段不要求學生掌握彈性勢能的表達式,但在探究過程中用到的微元思想和類比思想卻是要求學生理解和掌握的核心素養.所以教師在教學過程中應有意識地增加實際案例或實驗情境,帶領學生進行由淺入深的科學探究,提高學生的學科素養和能力.

