淺析歐姆定律形成過程中蘊含的科學思想和方法

劉展鷗

(上海市民辦新復興初級中學 上海 200081)

1 歐姆定律學史資料現狀

歐姆(G.S.Ohm)的探索歷程可以“凝練、升華的科學思維方式和科學研究方法”[1]很多.然而課堂中展現給學生的基本是歐姆1826年初的實驗研究成果.這樣會導致學生認為歐姆是在前人電壓、電流概念的基礎上獲得成果.歐姆更像是一個“勤勉且仔細的觀察者”[2].

究其原因是一般的學史著作,如文獻[3-4]等,涉及歐姆定律的篇幅較少,且極少發掘其科學方法與思想.電磁學為主的文獻[5-6]中歐姆定律內容較詳實,可惜從引用量看,中學教師很少關注.英文區也有類似情況:“……其中大多數都是德文,而且使用的術語是歐姆那個時代的,因此很難理解他的工作.”[7]所以文獻[2,7-10]從不同角度進行了研究,這些文獻絕大多數未被國內教師引用.

2 概念溯源

在歐姆所處的時代,電壓、電流、電阻3個概念要么是模糊的,要么根本不存在.當時人們認為電是一種可以流動的物質,稱為電流體,且有所謂“一流體”和“二流體”之爭.“二流體”假說認為有正負兩種電流體,若物體中有等量異種電流體時,呈電中性.“一流體”假說則認為只有一種電流體,物體多余電流體而帶正電,失去電流體而帶負電[5].從這里我們可以看出前人在電現象解釋過程中構建模型的科學思想.

如表1所示,人們把“電流體”和“熱量”作類比[11],還用溫度來比擬電勢(electrictension).

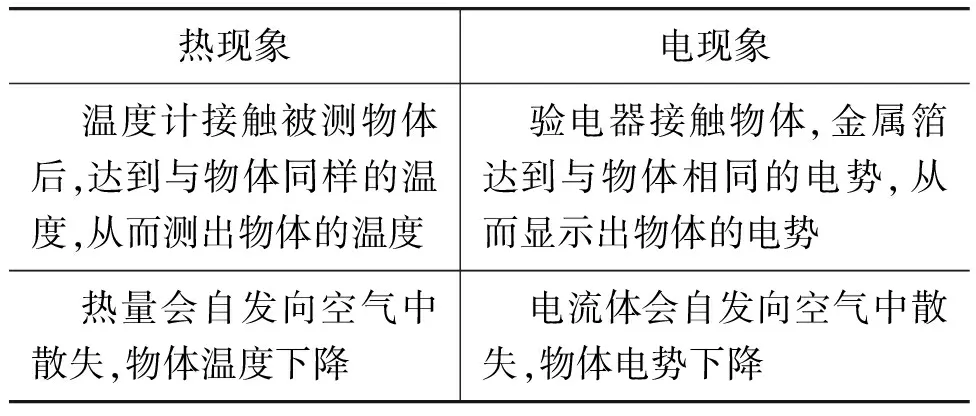
表1 電現象和熱現象類比

如圖1所示,兩個金屬板分別帶正負電,連接金屬板的驗電器金屬箔張開,表明金屬板有電勢,張開角度越大,說明電勢越大[2].如果用導線將兩塊金屬板連接起來,會產生瞬間的電流,伴隨著電中和金屬板上的電勢消失.

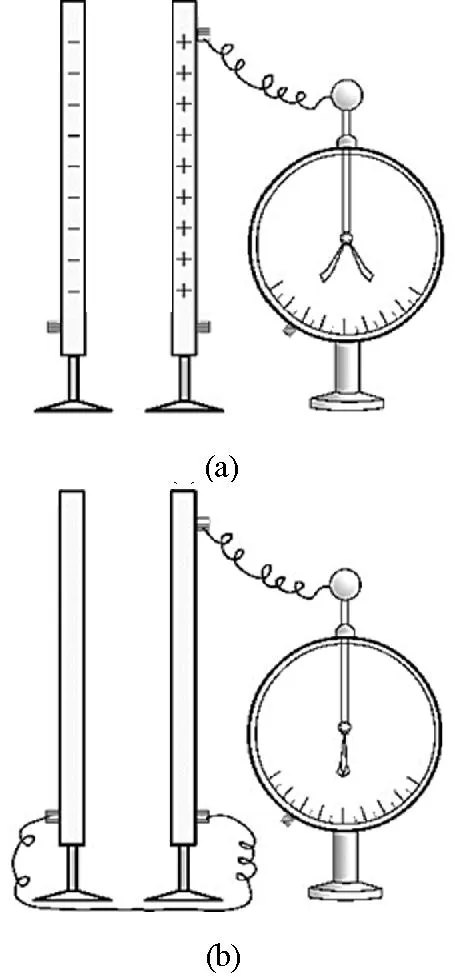
圖1 驗電器測電勢

如圖2所示,當時人們認為伏打電池中的激勵力(excitingforce)將正負電荷分離后產生電勢,情況就像圖1(a)一樣[2].當導線將電池兩端連接起來后,電池的電勢就會像圖1(b)一樣消失[2,7].

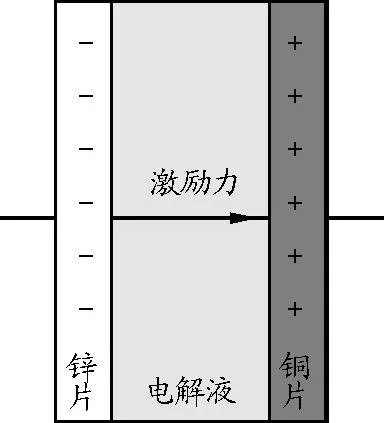
圖2 激勵力將正負電荷分離

因此,1820年安培(A.M.Ampère)區分了兩種電現象:電勢可以吸引輕小物體,能讓驗電器金屬箔張開等.電流則可以產生化學效應、熱效應和磁效應,電勢與電流是相互獨立的[2,8].

在歐姆那個時代,電流(intensityofcurrent)與電荷量(electricquantity)兩個概念有時邊界不清,電流與導體導電性能兩者的因果關系有時會顛倒[5,8].歐姆就是在這樣的背景下,開始了自己的探索,其工作大致可分為3個階段.

3 歐姆的探索

3.1 第一階段——導電性能

在第一階段歐姆想探索金屬導線的導電性能.在圖3[10]所示的實驗電路中,M、N和O是3個盛有水銀的杯子,歐姆通過觀察磁針的偏轉情況,判斷電流大小.

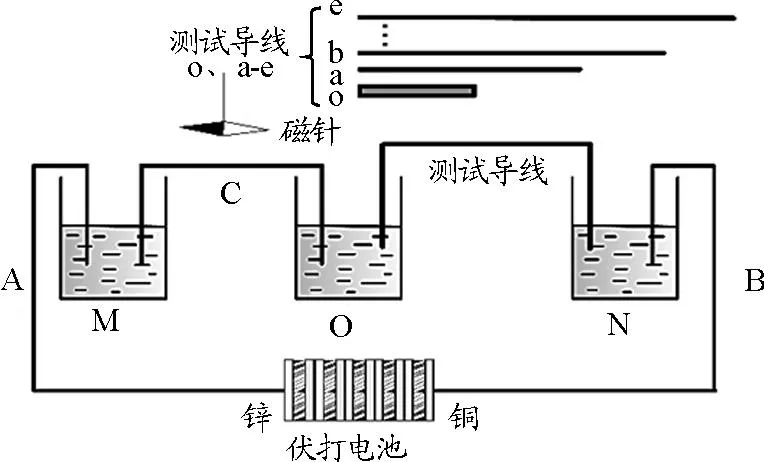
圖3 歐姆第一階段實驗電路

由于伏打電池極其不穩定,歐姆將一根又短又粗的導線o作為標準導線,每次先把標準導線o接入電路中的O和N之間,觀察磁針的偏轉作為“標準力”,然后再接入a～e中的某一根待測導線,觀察磁針的偏轉作為“較小力”[2,5].最后歐姆用以下公式計算了力損失(德語:kraftverlust,英語:lossofforce)

(1)

歐姆為了克服電池不穩定所造成的影響,每次用普通待測導線a～e做實驗的前后,都要測量標準導線o的情況作為基準,用式(1)對相關數據做歸一化(normalization)處理.使得不同電源電壓下的測量結果可以相互比較.這種測量方法在復雜多變的環境中,始終“錨定”一個參照物作為基準,本質上是一種相對測量,在經濟學和信息學中也大量應用.

歐姆還運用了插值法(表2)處理數據.

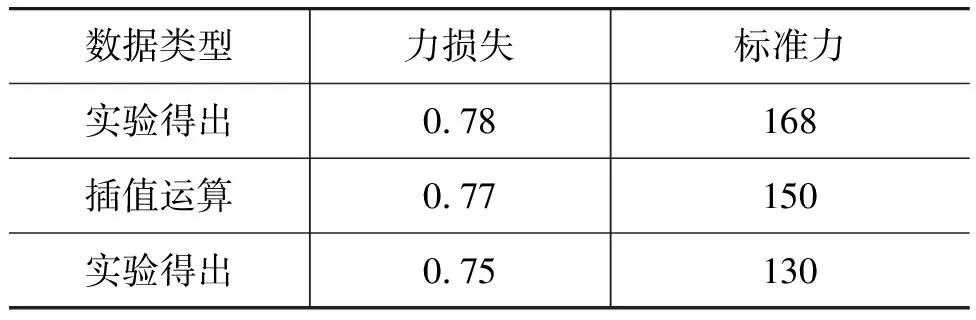
表2 歐姆對數據進行插值運算

插值運算并非捏造數據,而是依據數據變化趨勢并遵循一定原則進行的,插值運算過程本身也是一種擬合.通過插值的運算可以反推基于有限數據的初步結論是否正確,比如探究向心力F與角速度ω的關系時,可以讓學生基于他們的結論進行插值運算來驗證,他們的體驗一定更深刻.在實驗基礎上,歐姆先得出一個經驗公式,然后再將其推廣為以下公式

(2)

其中v是力損失,m是一個和電路相關的常量,x是測試導線的長度.a與圖3中其余部分導線A、B、C的長度有關.式(2)和歐姆定律相去甚遠,但是并非毫無意義,將其用泰勒級數展開并忽略高次項,可以得到

(3)

若圖3中電源電動勢為E,除測試導線以外的其余部分電阻與電源內阻之和為r.因為磁針的偏轉程度可以認為與測試導線中電流大小成正比, 所以“標準力”和“較小力”都可以用電流I來表示.由于測試線o的電阻小到可以忽略不計,當o接入電路時的電流為

設某測試導線的電阻為R,接入電路后電流為

“力損失”為

歐姆又用圖3所示裝置找出了若干根導電性能相同的金屬導線,這些導線的橫截面積相同而材料不同,其長度與金屬導電性能成正比,如圖4所示.在這個實驗中歐姆將不同金屬的導電性能轉化為可直接測量的導線長度.這種方法稱為“轉化法”.

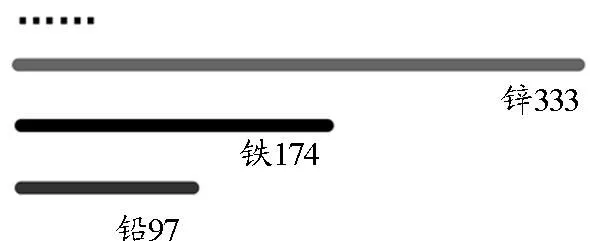
圖4 用長度表示不同金屬的導電性

當時的物理學家認為電路中的電流會因耗散而損失一部分,英國物理學家巴洛(P.Barlow)這樣設想,如果一流體理論正確,且電流在電路中會耗散,那電流從正極流向負極的過程中會越來越小,就會出現正極附近電流大于負極附近電流的情況.如果二流體理論正確,則即便不考慮電流耗散,兩種流體各自從電池的正負極出發,在中間會合后電中和,必定是電路中間的電流小于正負極附近的電流[5,8],巴洛的這種科學方法稱為“理想實驗”.最后巴洛通過實驗證明在同一個電路中,電流處處相等[8],說明了電流并非被電源內部的激勵力“推”出來后,就在電路中自由流動,這一結論對歐姆影響很大.

3.2 第二階段——基于證據

這一階段歐姆改用穩定的溫差電池作為電源,并制作了一套如圖5[9-10]所示的專用器材,其主要部分如圖6所示.

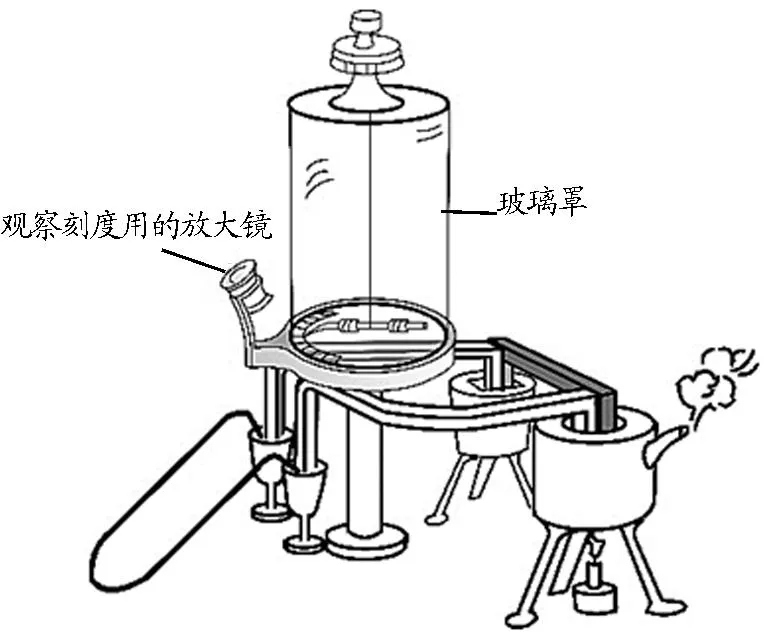
圖5 歐姆的實驗裝置

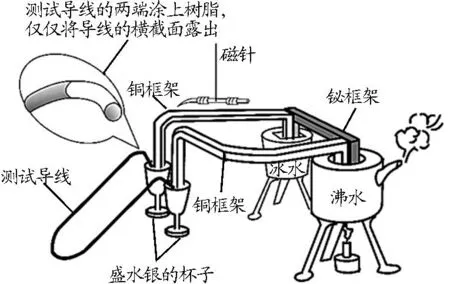
圖6 實驗裝置主要部分

歐姆用8根直徑相同長度不同的鍍銅鐵線分別接入電路進行實驗[5],一共進行了5次實驗,導線的長度和第1次實驗數據[6]如表3的第二列和第三列所示.

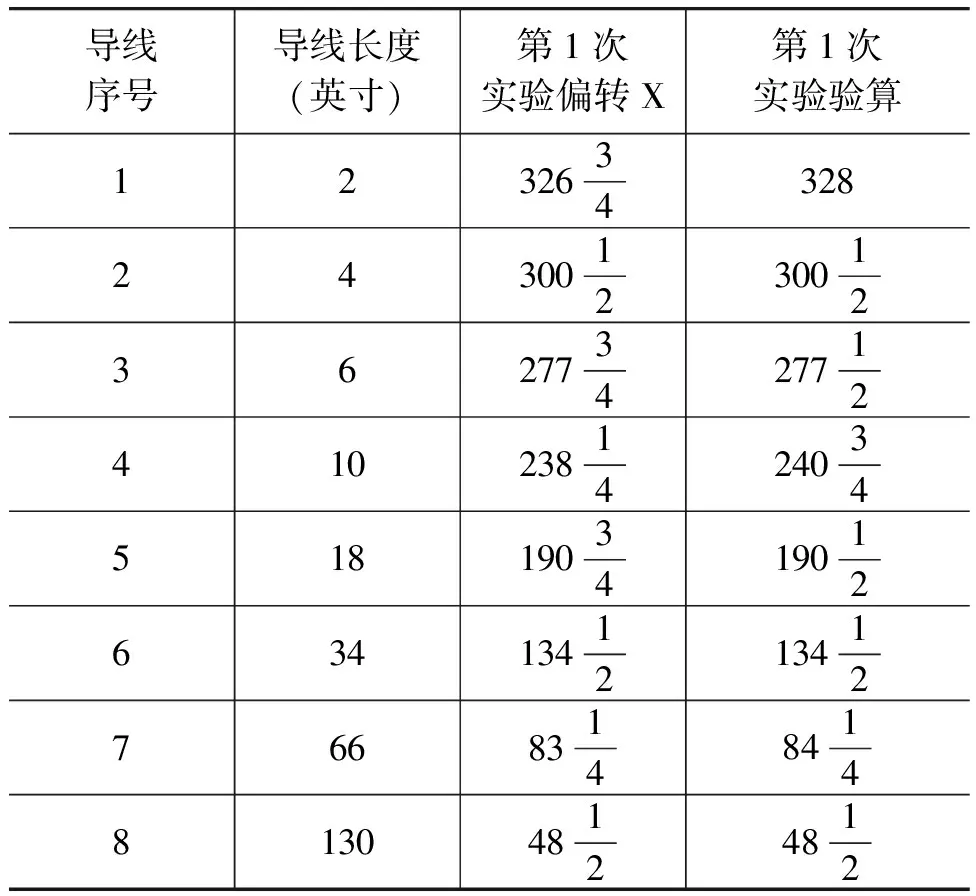
表3 歐姆部分數據和驗算

歐姆依據這些數據得出了以下公式

(4)

其中X是磁針偏轉角的百分度,可認為正比于電路中的電流,a與溫差電池的溫度差有關,相當于電源電動勢.b取決于除待測導體以外的電路其他部分的電阻,x是待測導體的長度.

為了驗證這個公式是否符合實際情況,歐姆令b=20.25,為每次實驗中的a賦了不同的值,比如第1次實驗中a=7 285,驗算結果如表3的第四列所示.歐姆依據實驗數據反復演算推導出公式,驗算后再實驗驗證.這種科學研究方法稱為“嘗試法”[5].

筆者利用軟件繪制了歐姆5次實驗的X隨x變化的圖像(圖7),發現歐姆選取的8根待測導線的長度也是很有講究的.前4根比較短,后4根長度陡然增大,長度之比接近1∶2∶4∶8,呈指數級增長.從圖像可以看出數據覆蓋非常完整,導線雖少但是具有普遍性,這種數據采樣的方法值得老師們學習.

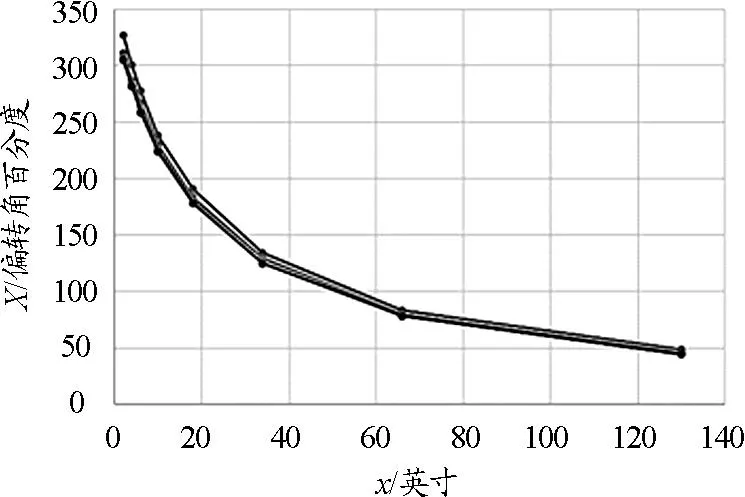
圖7 X-x圖像

3.3 第三階段——基于論證

1826年歐姆先后發表了兩篇論文,在第二篇論文中,歐姆將公式改寫為

(5)

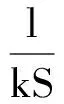
(6)

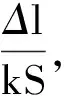
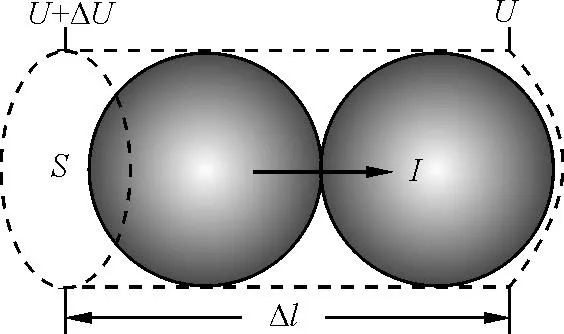
圖8 導體元

推導可得

一定會被這種微元法所折服.歐姆將復雜的情況進行理想化并抽象出本質的做法,是物理學理論研究的一種基本方法[6].

對比3個階段的工作就會發現,歐姆最終的觀點已經超越了他所處的時代[2,7].首先,他在第三階段工作中精確定義了電流的概念,而不是簡單地用磁針的偏轉角度X來表示電流.其次,從式(5)和式(6)可以看出歐姆已經認定了等效長度L是一個和電流、電勢差沒有關系的物理量,在后來的著作中,歐姆把這個物理量稱為電阻(德語:widerstand,英語:resistance)[7].

最為重要的是:歐姆引入了一個叫“電張力”(德語:spannung,英語:tension)的概念,因為術語對應的關系也被稱為電勢,但歐姆的電勢概念不同以往,而是在一個閉合電路中,每一點都有一個電勢[2].從電源的正極到負極,電勢會逐漸下降,電流則由電勢差和電阻共同決定.這說明歐姆的電勢概念已經很接近今天電勢(electricpotential)的概念了.

下面筆者用兩個模型來對比一下兩者的差別(圖9).如果采用適切的課堂活動讓初中生大致了解圖9中歐姆的電路模型,則更有利于他們建立正確的電壓概念.相信文獻[12]了解了上述史實,一定會結合歐姆的模型,引入電路的“人工瀑布”和“小朋友搬球”模型.

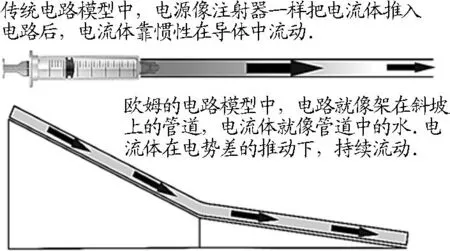
圖9 兩種電路模型的對比

綜上所述,毫不夸張地說“歐氏乃倡導電動勢,電流之強及電阻之精確觀念第一人也!”[4]“他理應得到偉大的榮譽”[3].

4 科學本質

歐姆的研究成果發表后,招致了很多批評.有人認為這是當時德國黑格爾主義盛行所致[3,5-6];也有人認為是歐姆的數學推導艱澀難懂[6,10],而文獻[2,7]分析后認為事情的本質是歐姆的理論創新和舊觀念產生了巨大的沖突,當時的物理學家鮑爾(G.F.Pohl)這樣批評歐姆:“閉合電路的定量磁效應取代了開路時的電現象,這是一個錯誤,……就像磁針突然代表了驗電器的功能一樣[2].”就這樣歐姆定律沉寂了十幾年后才被認可.

歐姆的探索歷程多被作為勵志故事加以宣揚,然而筆者認為其有更大的育人價值——“認識科學本質”[1].第一,歐姆敢于挑戰有著“電學牛頓”之稱的安培,說明科學講求質疑與創新,沒有絕對權威.第二,歐姆研究過程中概念逐漸清晰、模型日臻完善的過程,說明科學本質上是人類在觀察和推理的基礎上對客觀世界的逐步理解,而非絕對真相.第三,歐姆定律的建立運用了實驗研究、對比分析、數學推導等多種方法,說明了沒有絕對可靠的科學方法.第四,舊理論被否定,歐姆定律建立,歐姆定律又被證明有適用條件,說明科學定律只能在一定的條件范圍內是可靠的,不可能被絕對證明.這就是科學.