基于決策樹集成學(xué)習(xí)在癌癥風(fēng)險(xiǎn)分層中的應(yīng)用?

殷清燕 車露美 劉星宇

（1.西安建筑科技大學(xué) 西安 710055）（2.西安郵電大學(xué) 西安 710121）

1 引言

生存分析（Survival Analysis）是研究生存現(xiàn)象和響應(yīng)時(shí)間的一門統(tǒng)計(jì)學(xué)分支，已被廣泛運(yùn)用于醫(yī)學(xué)領(lǐng)域，如臨床試驗(yàn)、疾病診斷和預(yù)后分析等［1～4］。生存數(shù)據(jù)中經(jīng)常出現(xiàn)刪失數(shù)據(jù)，導(dǎo)致生存時(shí)間信息不完全。傳統(tǒng)的統(tǒng)計(jì)學(xué)習(xí)方法無法很好地解決生存刪失數(shù)據(jù)的分析。設(shè)計(jì)適用于生存分析的機(jī)器學(xué)習(xí)算法，具有重要的研究意義和應(yīng)用價(jià)值。

TCGA 是由美國國家癌癥研究所和人類基因組研究所合作建立的可公開獲取的癌癥組學(xué)數(shù)據(jù)庫［5］。TCGA 收錄了33 種癌癥數(shù)據(jù)，包含四種類型的 生 存 事 件：OS（Overall Survial），PFI（Progression-Free Interval），DFI（Disease-Free Interval），DSS（Disease-Specific Survival）。OS 指從觀察開始到死亡的時(shí)間；PFI 指從觀察開始到腫瘤進(jìn)展的時(shí)間；DSS是指從診斷或治療開始到死亡的時(shí)間；DFI指治療后無病狀態(tài)到腫瘤進(jìn)展的時(shí)間，進(jìn)展事件可能是局部復(fù)發(fā)和遠(yuǎn)處轉(zhuǎn)移。本研究首先選擇OS和PFI 事件進(jìn)行初步Kaplan-Meier 估計(jì)，OS 事件進(jìn)行深入的生存分析。

2 生存分析方法

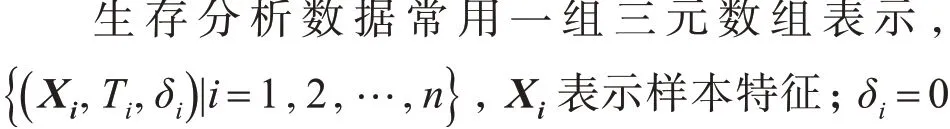
2.1 隨機(jī)生存森林

盡管Cox 比例風(fēng)險(xiǎn)模型在生存分析領(lǐng)域非常流行，但是比例風(fēng)險(xiǎn)假設(shè)在高維生存數(shù)據(jù)上難以成立。為了緩解這個(gè)問題，研究者們提出了具有較少的約束模型假設(shè)的非參數(shù)方法。隨機(jī)生存森林（Random Survival Forset，RSF）是Ishwaran提出的一種適用于生存數(shù)據(jù)的決策樹集成方法［9］。RSF 算法提出了CART 決策樹框架下的生存樹分裂規(guī)則，即將結(jié)點(diǎn)分裂成具有不相似生存時(shí)間的左右子結(jié)點(diǎn)，選取最大化結(jié)點(diǎn)間生存差異的特征作為最佳分裂特征。

RSF 算法通過Bootstrap 隨機(jī)采樣數(shù)據(jù)生成生存樹；分割節(jié)點(diǎn)時(shí)使用隨機(jī)選擇的特征子集；生存樹完全生長不進(jìn)行剪枝；將多個(gè)生存樹的預(yù)測結(jié)果進(jìn)行多數(shù)投票得到最終的預(yù)測。

2.2 梯度提升生存樹

表1 梯度提升生存樹的算法流程

成分梯度提升（CW-GBM）是2016 年提出的基于boosting和穩(wěn)定性選擇的梯度提升方法［12］。可以提高計(jì)算可行性，在穩(wěn)定性選擇中引入隨機(jī)排列來達(dá)到控制假陽性率。

3 Kaplan-Meier估計(jì)

原始的TCGA 數(shù)據(jù)集包含33 種癌癥類型的10915 個(gè)患者信息。本研究對(duì)原始數(shù)據(jù)進(jìn)行數(shù)據(jù)清洗，得到預(yù)處理后的5384 個(gè)患者生存數(shù)據(jù)。生存信息包括OS，OS.time，PFI，PFI.time，臨床特征包括年齡、性別、腫瘤狀態(tài)和病理分期等。

Kaplan-Meier 估計(jì)通常是進(jìn)行生存分析的第一步。根據(jù)離散的生存時(shí)間估計(jì)生存概率，繪制Kaplan-Meier 生存曲線，觀察和比較不同組患者的生存狀況。根據(jù)腫瘤狀態(tài)特征將患者分為有腫瘤和無腫瘤，分別繪制生存曲線（圖1）。上圖表示OS事件的生存曲線，無腫瘤的最低生存概率約為0.55，有腫瘤的生存曲線下降非常快；下圖表示PFI事件的生存曲線，無腫瘤的最低生存率約為0.72，有腫瘤的生存曲線下降得最快。有腫瘤的生存概率均在2000 天后低于0.1，有腫瘤和無腫瘤的生存曲線之間的差別非常大。有腫瘤的OS生存曲線和PFI 生存曲線具有相同的趨勢(shì)，PFI 生存曲線下降速度更快。

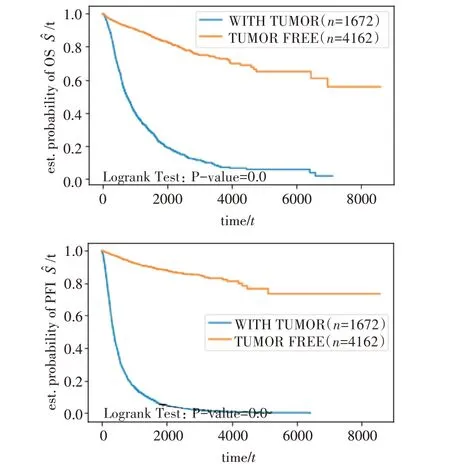
圖1 不同Tumor status下的K-M曲線

根據(jù)性別特征將患者分為男性（Male）和女性（Female），繪制生存曲線（圖2）。男性患者的OS和PFI 生存曲線均低于女性患者，男性患者的生存概率低于女性患者。男性和女性患者在PFI 生存曲線上的差別更大。

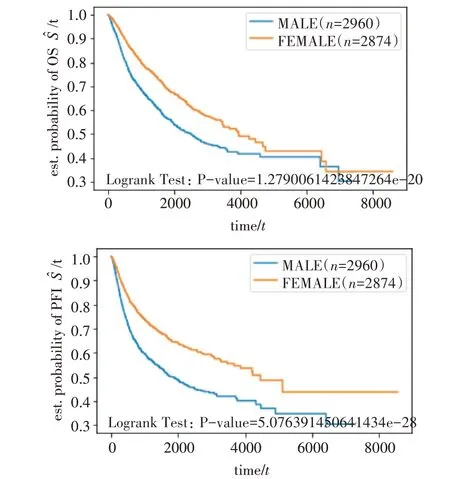
圖2 不同性別的K-M生存曲線

根據(jù)病理分期特征將患者分為六組。根據(jù)癌癥分期將患者分為六期，分別繪制曲線（圖3）。I/II/III 的最低生存概率分別約為0.51、0.28、0.21，癌癥四期（Stage IV）在t=2000 時(shí)的生存概率小于0.3。在t=3000 時(shí)不同病理分期的生存曲線之間有明顯的差別，病理分期等級(jí)越高的患者生存概率越低。

圖3 不同Stage下的K-M生存曲線

根據(jù)不同癌癥類型將患者進(jìn)行分組，繪制生存曲線比較不同癌癥類型患者的生存狀況（圖4）。所有癌癥類型的患者在t=2000天（約5.5年）時(shí)達(dá)到最低生存概率。癌癥患者的生存概率與癌癥類型，性別，腫瘤狀況（Tumor status）和病理分期（Stage）相關(guān)。

圖4 不同癌癥類型的K-M生存曲線

4 生存風(fēng)險(xiǎn)預(yù)測

4.1 超參數(shù)的貝葉斯優(yōu)化

本文使用OrdinalEncoder 對(duì)“cancer type”，“tumor_stage”，“tumor_status”進(jìn) 行 編 碼；使 用One-HotEncoder 對(duì)“gender”特征進(jìn)行編碼，使用StandardScaler 對(duì)“age”進(jìn)行標(biāo)準(zhǔn)化。采用貝葉斯超參數(shù)優(yōu)化方法對(duì)每個(gè)算法的超參數(shù)進(jìn)行調(diào)整［13］。橫坐標(biāo)表示參數(shù)的調(diào)參范圍，縱坐標(biāo)表示一致性指數(shù)（C-index）值，繪制各個(gè)算法模型的超參數(shù)優(yōu)化過程圖。

圖5 是CW-GBM 算法的調(diào)參結(jié)果圖。隨著“n_estimators”的增大，模型的C-index 保持增大。n_estimators 達(dá)到300 之后，C-index 指數(shù)趨于穩(wěn)定，選擇最優(yōu)n_estimators=493。圖6 和圖7 是GBM 和RSF算法的調(diào)參結(jié)果圖。“min_samples_leaf”的調(diào)參范圍是（1，25），min_samples_split 的調(diào)參范圍是（2，25），max_features 的調(diào)參范圍是（1，5），C-index 取值（0.80，0.82）。GBM 選取的最優(yōu)超參數(shù)為min_samples_leaf=9，max_features=2，min_samples_split=11，n_estimators=188。RSF 算法選取的最優(yōu)超 參 數(shù) 為min_samples_leaf=3，max_features=1，min_samples_split=16，n_estimators=21。

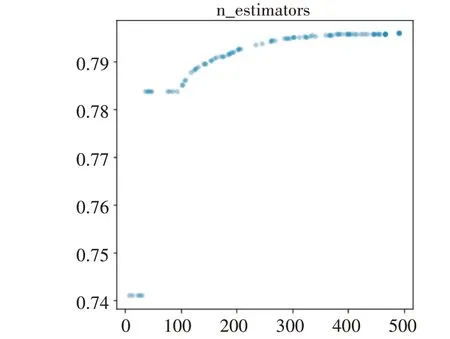
圖5 CW-GBM模型的超參數(shù)優(yōu)化

圖6 GBM模型的超參數(shù)優(yōu)化

圖7 RSF模型的超參數(shù)優(yōu)化

C-index 在0.5～1 之間，0.5 為完全不一致,說明該模型沒有預(yù)測作用，1 為完全一致，說明該模型預(yù)測結(jié)果與實(shí)際完全一致。一般情況下C-index在0.50～0.70 為準(zhǔn)確度較低：在0.71～0.90 之間為準(zhǔn)確度中等；而高于0.90 則為高準(zhǔn)確度。各算法在TCGA 測試集上的C-index 見圖8。RSF、GBM、COX、CW-GBM 在測試集上的一致性指數(shù)依次為0.87、0.85、0.79 和0.79。RSF 模型在預(yù)測測試集上的表現(xiàn)較好，具有較高的準(zhǔn)確性。

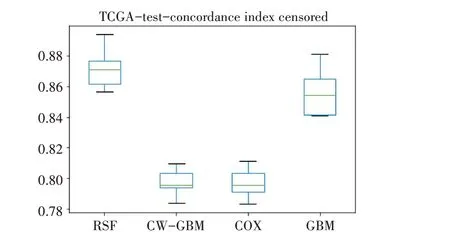
圖8 各算法在TCGA測試集上的C-index

圖9 是各算法的time-dependent AUC 曲線圖，虛線表示AUC平均值［14］。Cox PH模型的AUC平均值為0.84，最低值為0.65。觀察初期的AUC值增長較塊，約1000 天后達(dá)到AUC 平均值。RSF 和GBM算法的AUC 曲線位于CoxPH 曲線上方，RSF 和GBM算法的性能優(yōu)于CoxPH。因此，基于貝葉斯超參數(shù)優(yōu)化的RSF和GBM具有較好的性能。

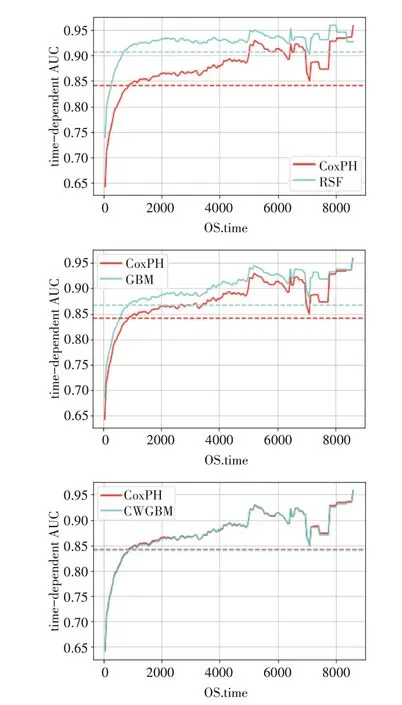
圖9 各算法在TCGA數(shù)據(jù)集上的AUC

4.2 生存風(fēng)險(xiǎn)分層預(yù)測

選擇性能表現(xiàn)優(yōu)異的隨機(jī)生存森林和梯度提升樹進(jìn)行癌癥患者的生存風(fēng)險(xiǎn)分層。根據(jù)預(yù)測的風(fēng)險(xiǎn)評(píng)分值的四分位數(shù)，將患者分為四個(gè)風(fēng)險(xiǎn)組：低危組、中低危組、中高危組和高危組［15］。在隨機(jī)生存森林RSF中選取的風(fēng)險(xiǎn)評(píng)分分界點(diǎn)為0～1.84，1.84～8.45，8.45～22.53，22.53～100。在梯度提升樹GBM 算法中選取的風(fēng)險(xiǎn)評(píng)分分界點(diǎn)為0～15.96，15.96～29.33，29.33～43.54，43.54～100。

RSF 風(fēng)險(xiǎn)評(píng)分的四分位數(shù)分別為1.84，8.45，22.53，據(jù)此劃分的低危組1459 例、中低危組1458例、中高危組1167 例，高危組1750 例。GBM 風(fēng)險(xiǎn)評(píng)分的四分位數(shù)分別為15.96，29.33，43.54，據(jù)此劃分的低危組1461例、中低危組1458例、中高危組1165 例，高危組1750 例（表2）。RSF 和GBM 四個(gè)風(fēng)險(xiǎn)組的生存曲線如圖10 所示。可見兩個(gè)算法中相鄰風(fēng)險(xiǎn)組的生存曲線均有顯著性的差異。風(fēng)險(xiǎn)評(píng)分較高的風(fēng)險(xiǎn)組的生存曲線也較低，表明生存風(fēng)險(xiǎn)分層方法的有效性。

圖10 四個(gè)風(fēng)險(xiǎn)組的KM生存曲線

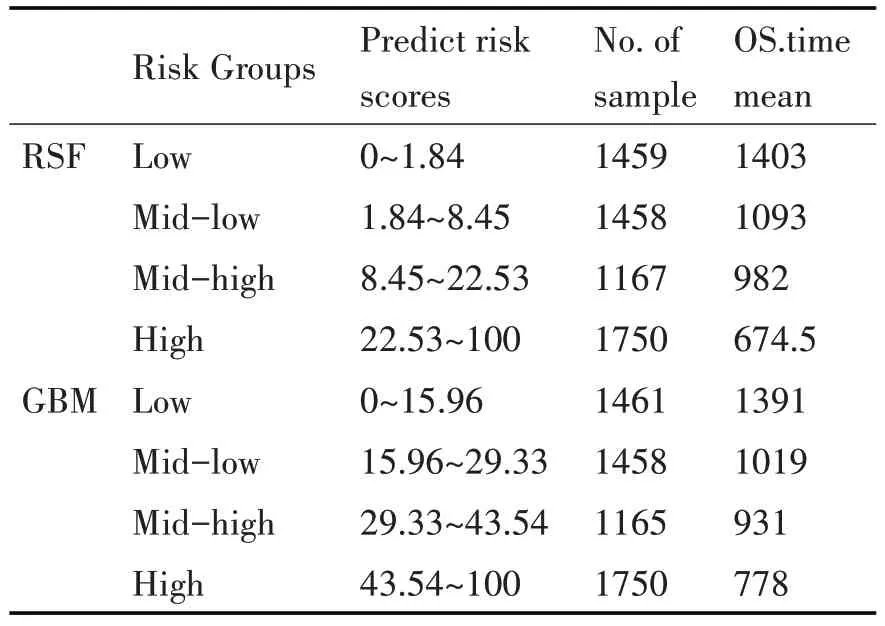
表2 TCGA患者的風(fēng)險(xiǎn)分層

結(jié)合表3 各風(fēng)險(xiǎn)組在性別、年齡、腫瘤狀態(tài)等方面的差異。在性別方面，我們可以看到各風(fēng)險(xiǎn)組中女性的數(shù)量普遍較低，尤其在RSF 低風(fēng)險(xiǎn)組中，女性人數(shù)僅為9 人，而男性人數(shù)為484 人。隨著風(fēng)險(xiǎn)程度的提高，男性人數(shù)逐漸增多，而在GBM 高風(fēng)險(xiǎn)組中，男性人數(shù)高達(dá)1078 人，女性人數(shù)也有667人。這表明，隨著年齡的增長，男性患腦腫瘤的風(fēng)險(xiǎn)較高。在年齡方面，我們可以看到各風(fēng)險(xiǎn)組的年齡分布有所不同。在RSF低風(fēng)險(xiǎn)組中，平均年齡為47.98歲，隨著年齡的增加，風(fēng)險(xiǎn)組平均年齡也逐漸上升。在GBM 高風(fēng)險(xiǎn)組中，平均年齡為64.7 歲，這說明隨著年齡的增長，患腦腫瘤的風(fēng)險(xiǎn)也在增加。

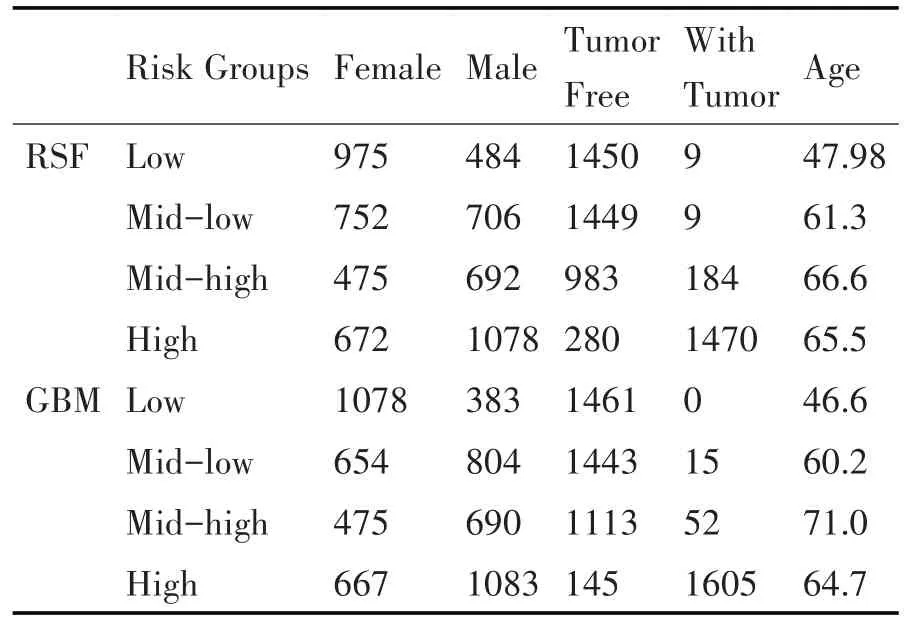
表3 各風(fēng)險(xiǎn)組的信息

針對(duì)不同風(fēng)險(xiǎn)組的特征信息進(jìn)行分析，結(jié)果表明腫瘤狀態(tài)對(duì)患者生存風(fēng)險(xiǎn)的作用最顯著。隨著年齡的增長，男性患腦腫瘤的風(fēng)險(xiǎn)較高；患者的腫瘤狀態(tài)為“With tumor”時(shí)，患者的生存風(fēng)險(xiǎn)較高；其次年齡特征對(duì)患者生存風(fēng)險(xiǎn)的影響顯著。相比高風(fēng)險(xiǎn)組，低風(fēng)險(xiǎn)組患者的平均年齡較低。因此，針對(duì)不同風(fēng)險(xiǎn)組的人群，應(yīng)采取有針對(duì)性的預(yù)防措施，以降低腦腫瘤的發(fā)病風(fēng)險(xiǎn)。

5 結(jié)語

本研究針對(duì)TCGA 癌癥患者生存數(shù)據(jù)，比較CoxPH 模型、隨機(jī)生存森林RSF、梯度提升樹GBM和CW-GBM 算法的生存分析性能。對(duì)各個(gè)算法進(jìn)行貝葉斯超參數(shù)優(yōu)化，獲得C-index 和time-dependent AUC性能評(píng)價(jià)值。結(jié)果表明，隨機(jī)生存森林和梯度提升樹優(yōu)于其他模型，在測試集上C-index 為0.87，time-dependent AUC 為0.90。其次，基于RSF和GBM 的生存風(fēng)險(xiǎn)評(píng)分，進(jìn)行癌癥患者的生存風(fēng)險(xiǎn)分層，劃分為低危組、中低危組、中高危組和高危組。KM 生存曲線的實(shí)驗(yàn)結(jié)果表明，隨機(jī)生存森林和梯度提升樹算法對(duì)TCGA 癌癥患者的生存風(fēng)險(xiǎn)具有很強(qiáng)的預(yù)測能力，在識(shí)別高危和低危患者群體方面有著顯著的判別作用。