融合密度和劃分的文本聚類算法?

劉 龍 劉 新 蔡林杰 唐 朝

（湘潭大學計算機學院·網絡空間安全學院 湘潭 411105）

1 引言

近幾十年來，隨著計算機技術的快速發展，人們獲取的信息和采集的數據越來越多，但是海量的數據缺乏有效的處理，人們就很難得到有效且有用的信息。基于此種情況，作為數據挖掘的一種有效工具，聚類算法［1］可以幫助人們高效分析數據之間的關系。

本文研究文檔聚類［2］，文檔聚類的首要任務是文本向量化，將文檔轉換為高維向量再進行聚類。2013 年，谷歌推出了基于神經網絡訓練的Word2vec［3］詞向量模型，極大地促進了自然語言處理的發展；谷歌在2018 年再次發布了基于深度學習的BERT［4］模型，該模型刷新了自然語言處理領域中多個方向的記錄。

文檔聚類的核心任務是研究聚類算法，但是密度聚類算法［5］在高維數據集上的表現非常差。劃分算法中的K-均值算法［6］效果一般，主要原因是算法的初始化［7］是隨機生成的。近年來，為了克服選取中心點為離群點，李武等［8］提出一種啟發式算法來逐步選取初始類中心點，選取的原則是初始類中心點差異度高且與其他初始類中心點差異度高，實驗表明該算法聚類效果正確率高，收斂速度快。賈瑞玉等［9］提出利用局部密度和決策樹來確定K-均值算法的類簇中心點的數量和位置，該方法可以有效地排除特殊點，在低維上有著不錯的效果。王思杰等［10］提出基于距離的離群點檢測技術，對中心點進行篩選，避免離群點成為中心點。張國峰等［11］提出逐步選取類簇中心點，在更新中心點的同時判斷簇點的合理性并及時做出修改，這種方法確保了不會出現空簇。Rodriguez等［12］在Science上提出了一種新的密度聚類算法，該算法的思想是聚類中心的密度高于其鄰近的中心且距其他高密度點相對較遠。

本文使用BERT 模型來處理文本向量化，并且與其他方法進行實驗比較，BERT 模型的確具有出色的性能。本文還提出了一種結合密度和劃分的文本聚類算法，與其他幾種聚類算法相比，該算法對高維數據集具有更好的聚類效果。

2 相關工作

2.1 文本向量化表示

文本聚類一個重要過程就是文本的向量化。文本向量方法有傳統的向量空間模型［13］（VSM）和Word2vec 方法，兩者需要結合文本特征提取TF-IDF［14］方法來進行文本聚類。Word2vec 方法優點是簡單、快捷、易懂，但也存在著比較嚴重的問題，它非常依賴語料庫，需要選取質量較高且和所處理文本相符的語料庫進行訓練。

本文使用BERT 模型來處理文本的向量化，BERT 模型作為Word2vec 的替代者，它的網絡架構使 用 了 多 層 帶 有Attention［15］的Transformer［16］結構。本文使用的是BERT-Base 中文模型，模型有12 層Transformer 編碼器，隱藏層的維度是768，自注意頭的個數為12，其中BERT 模型中一個Transformer編碼器的計算過程如下：

1）文本向量：通過詞向量化將單詞變成向量x1、x2…xm，文本向量X的維度是m×768，m為句子的最大分詞數；

2）計算Q、K、V：這里我們通過模型的參數WO、WK、WV結合輸入向量X來計算出來向量Q、K、V：

3）單頭自注意力層的輸出矩陣Z：這里首先計算詞在上下文中的意義以及詞之間的影響QK，得到之后進行歸一化處理，最后加權平均得到單頭注意力層輸出矩陣Z：

4）融合所有注意力頭信息的矩陣Zsum：BERT模型使用了12個注意力頭，經過步驟3）后，我們可以得到12 個不同的Z 矩陣，乘上附加的權重矩陣WO可得到Zsum，Zsum的維度為m×768，最后經過殘差連接和求和歸一化即為下一層下面Transformer 編碼器的輸入。公式中concat（Zi）表示為12 個注意力頭輸出矩陣的拼接：

2.2 文本距離計算

文本聚類過程中需要計算文本間的差異，本文使用歐氏距離來計算文本距離，歐氏距離可以有效防止過擬合，還可以讓距離優化求解快速和穩定。文本距離計算公式如下：

注：D（X，Y）表示文本X與文本Y的歐氏距離。該值越小代表著兩個文本屬于同一類別的可能性越高。反之，該值越大則說明文本相似度越小。xi與yi分別表示文本X、Y的某一向量維度值。

3 文本聚類算法

3.1 K-means算法

K-means算法屬于劃分聚類算法，該算法是將數據集n個數據對象劃分成K類，其具體步驟是：

1）任意選擇K 個樣本點當做初始類中心點，每個初始類中心點作為一個聚類中心；

2）對于數據集中的所有樣本點，計算其與每個聚類中心的距離，將其歸為距離最近的聚類中心類簇；

3）將各個類簇樣本點的均值作為該類簇新的聚類中心，得到新的K個聚類中心；

4）重復步驟2）～3），并在每次迭代后計算是否滿足停止條件，若達到條件之一，則輸出結果。

K-means算法的停止條件一般為以下三種：聚類中心與前一次聚類中心相差極小；重新劃分給其他類簇的樣本點極少；目標函數極小，即數據集的誤差平方和（SSE）局部最小。誤差平方和計算如式（7）至式（8）所示：

注：SSE 參數計算表示當前的聚類情況的所有樣本點到各自劃分類的聚類中心的距離總和，這個值越小表示當前的聚類效果越好。K表示聚類類別。Ci表示單個類簇，共K 個類簇。p 表示樣本點向量。mi表示類中心點向量，是類Ci的均值向量，也稱質心。x表示類簇Ci中的向量。

3.2 K-means++算法

K-means++算法［17］主要解決K-means 算法受初始化影響大的問題，在選擇初始類中心點方面做了改進，保證初始點足夠離散。算法初始化類中心點的具體步驟如下：

1）任選某一樣本點當做初始類中心點；

2）計算其余樣本點與最近初始類中心點的距離，用D（x）表示；

3）通過樣本點的D（x）來表示其成為初始類中心點的概率P；

4）最后輪盤法選擇出下一個初始類中心點；

5）重復步驟2）～4）直至得到K 個初始類中心點。

關于K-means++算法的初始化過程中參數D（x）和P，D（x）為文本向量的歐氏距離，具體計算見式（6），概率P計算如式（9）所示：

K-means++算法的初始化有效地改善了隨機初始化的不穩定性，選取下一個聚類中心點的概率與距離掛鉤，使得初始類中心點離散。

3.3 最大距離法

2014 年，翟海東等［18］提出使用最大距離法來選取初始類中心點。采用最遠距離的逐步選取類中心點，最大距離法選取類中心點流程如下：

1）計算n 個樣本點兩兩之間的距離，找到滿足D（c1，c2）≥D（ci，cj）（i，j=1，2，…，n）的兩個樣本點c1和c2，并將它們作為兩個初始類中心點；

2）在剩余的（n-2）個樣本點中，選取滿足D（c1，c3）×D（c2，c3）≥D（c1，ci）×D（c2，ci）的樣本點c3，將c3 作為第三個初始簇中心，ci 是除c3 外的任一樣本點；

3）依此類推，直至選取K個中心點。

最大距離法屬于K-means++算法的優化，聚類的初始化簇中心點確實有效地囊括所有數據，促使所選中心點的分布離散且合理。但是該方法極易選中離群點，導致聚類效果不理想。關于此類方法，還有基于子空間的K-means++優化算法［19］和K-meansⅡ算法［20］。

3.4 融合密度和劃分的聚類算法

本文提出了一種結合密度和劃分的文本聚類算法（CDP 算法）。首先通過距離計算來定義樣本點的密度，然后通過密度來選擇適合作為中心點的樣本，然后通過最遠距離方法逐漸選擇初始聚類中心點，最后根據距離對整個數據集進行劃分。算法具體步驟如下：

1）使用文檔距離計算模型計算n 個樣本集兩兩之間的距離dij；并計算所有樣本之間的平均距離dc，給出dc計算如式（10）所示：

2）根據樣本之間距離與樣本平均距離大小計算出每個樣本的密度?i，并計算所有樣本的密度ρi，給出ρi和ρc計算如式（11）～（13）所示：

3）將所有滿足ρi>ρc的樣本點歸入適合作為初始類中心點集合M，核心點集M 的個數m 必須滿足n>m>K；

4）在M 集合中隨機選取一點c1 作為初始類中心點；

5）在（m-1）個點中，選擇滿足D（c1，c2）≥D（c1，ci）的樣本點c2，ci是M集合中除c2的任一點；

6）在（m-2）個點中，選擇滿足D（c1，c3）×D（c2，c3）≥D（c1，ci）×D（c2，ci）的樣本點c3，ci 是M 集合中c3的任一點；

7）依此類推，直至得到K個初始類中心點；

8）根據距離計算將所有樣本點分配至與其相距最小類簇里；

9）重新計算中心點，類簇中全部樣本的均值就是新中心點；

10）重復步驟8）～9），直至數據集的SSE目標函數不變或者變化極小。注：dc表示截斷距離，即文檔數據集的樣本平均距離，計算數值是每一個文檔與其他文檔之間的文本距離總和平均化后得到的數值，當數據集確定后，該值為常數。ρi表示為單個文檔Xi的密度，若兩個文本的文本距離若小于樣本平均距離dc，說明兩個文本距離較近，即文本相似度較高，文檔Xj在文檔Xi的密度領域內，該值越大說明文檔Xi的附近點越多。ρc表示截斷密度，計算數值是所有文檔的密度平均值，當文本集確定后，該值也為常數。

4 實驗

4.1 數據集

本文實驗使用的數據集來自清華大學的的THUCNews 新聞文本分類數據集，THUCNews 數據集是根據新浪新聞2005～2011 年間的歷史數據篩選過濾生成，包含74 萬篇新聞文檔，均為UTF-8 純文本格式。此數據集在原始新浪新聞分類體系的基礎上，重新整合劃分出14 個候選分類類別：財經、彩票、房產、股票、家居、教育、科技、社會、時尚、時政、體育、星座、游戲、娛樂。該數據集的每篇文檔所包含的字數在300～5000之間。

4.2 評估標準

此次實驗使用的評判標準主要是F1 值，其次還有文本聚類耗時T。F1 值由精確率P（precision）和召回率R（recall）的計算得到，精確率P 值為所有“正類判定為正類”占所有“檢測是正類”的比例，召回率R值是所有“正類判定為正類”占所有“樣本是正類”的比例。P、R、F1 值的計算如式（14）～式（16），其中，TP表示“正類判定為正類”，FP表示“負類判定為正類”，FN表示為“正類判定為負類”。

4.3 實驗對比

4.3.1 文本向量化實驗

本次實驗目的是測試不同的方法處理文檔向量化的效果。實驗數據集是5 類文檔集，每一類文檔集有300 篇文檔。實驗首先使用不同方法將文檔轉為向量，然后使用傳統的K-means算法對文檔向量集進行聚類，將聚類的結果作為評判標準，實驗僅文檔向量化處理過程不一樣，其他均一致。實驗的兩種文檔向量化處理方法分別是BERT 模型、Word2vec。實驗結果如圖1所示。

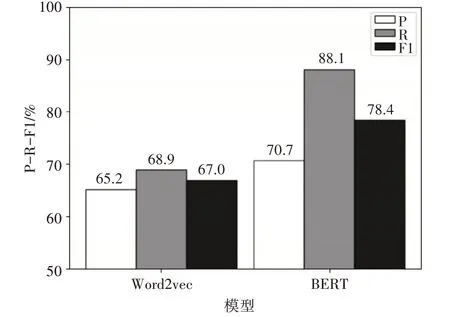
圖1 Word2vec與BERT關于文本向量化處理對比圖

從實驗結果可以看到在P、R、F1 值上，BERT均領先Word2vec，在F1 值上提高超過10%。在文檔向量化處理效果上，BERT 模型要優于Word2vec方法。

4.3.2 文檔關于類別數量變化實驗

本次實驗目的是測試聚類效果關于文檔類別數量的變化。對比實驗分成兩類：K-means 算法、本文提出的CDP算法。每一類分成七組試驗：第一組實驗的數據集包含3 類，每一類100 篇共300 篇文檔；第二組實驗的數據集包含4類，每一類100篇共400篇文檔；以此類推，第七組實驗的數據集是9類共900篇文檔。每一組實驗均采用BERT模型處理文檔向量化，每組實驗過程一致，僅實驗數據集不一樣。聚類指標隨類別數量變化如圖2所示。

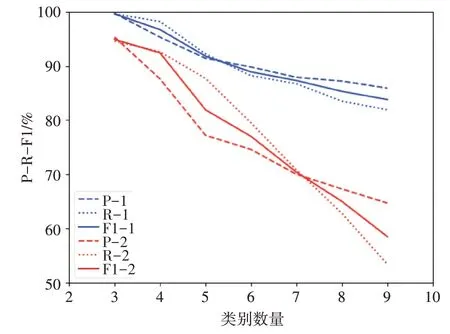
圖2 聚類指標隨類別數量變化圖

實驗結果中，紅色線數據為K-means 算法，采用隨機化初始化，藍色線數據為CDP算法。從實驗結果可以知道文檔聚類的F1 值會隨著文本類別的增加而降低，當K值較小時，F1值很高，當K值增加時，F1 值逐漸降低。使用CDP 算法后，聚類效果更好且穩定，在聚類類別小于10時，文檔聚類的F1值一直超80個百分點。

4.3.3 文檔關于文檔集數量變化實驗

實驗三：本次實驗目的是測試聚類效果關于文檔數據集數量的變化。對比實驗分成兩類：K-means 算法、CDP 算法。每一類分成六組對比實驗，每組實驗都是5 類文檔，只有文檔數量不一致，實驗分別對每組進行聚類取平均值：第一組實驗包含5 類，每一類100 篇共500 篇；第二組實驗包含5類，每一類200 篇共1000 篇；以此類推，第六組是5類共3000 篇文檔。每一組實驗均使用BERT 模型處理文檔向量化，實驗過程一致，僅實驗數據集不一樣。聚類指標隨文檔數量變化如圖3所示。

圖3 聚類指標隨文檔數量變化圖

實驗結果中，紅色線數據為K-means 算法，采用隨機化初始化，藍色線數據為CDP算法。實驗表明在文本類別不變的情況下，文檔的數量增加也會導致聚類的F1 值下降。數據顯示在K 值不變的情況下，兩類對比實驗的召回率R 值都在90%左右變動，精確率P 隨著文檔數量的增加而逐漸下降，從而導致F1 值的下降。說明文檔聚類會隨著文檔集數量增加而降低，兩類對比實驗的F1 值下降程度都較為穩定。

4.3.4 綜合對比實驗

實驗四：本實驗選擇兩組數據，第一組為5 個類別，每個類別100 篇共500 篇文章；第二類是5 個類別，每個類別有400篇共2000篇文章。測試算法有5種組合：算法1是一種傳統的K-means算法，使用Word2vec 做向量化處理；算法2 是K-means 加BERT 來處理文本向量化；算法3 是K-means++算法加BERT 來處理文本到向量的算法；算法4 是最大距離法（MDM）加BERT 處理向量化；算法5 是本文提出的CDP 算法，并結合BERT 處理文本向量化。每組實驗數據集均一致，采用5 種算法，最后多次實驗取均值作為實驗結果。第一組實驗結果如表1，第二組結果如表2。

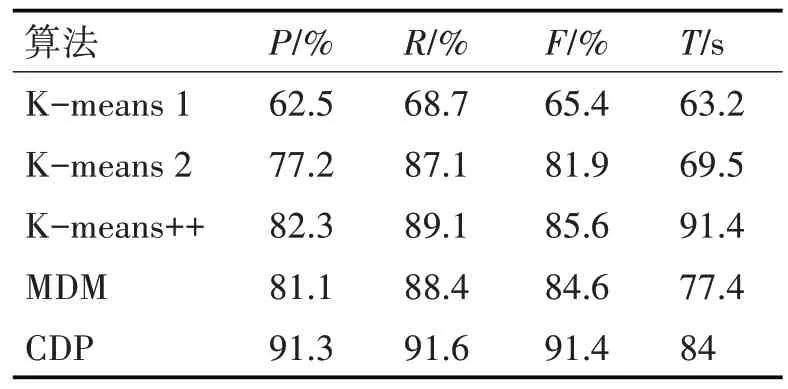
表1 綜合實驗一

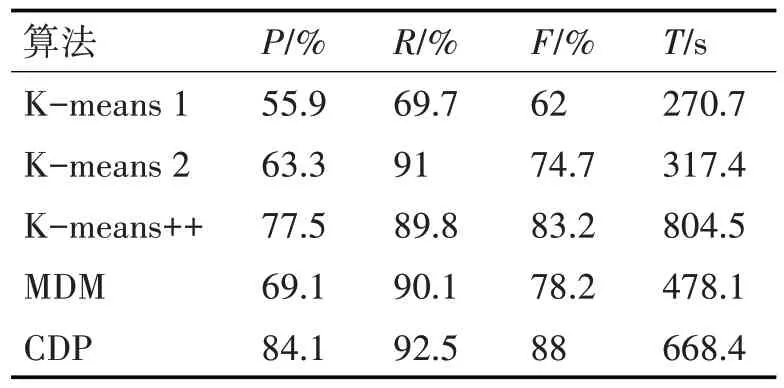
表2 綜合實驗二

根據表1 和表2 的數據，比較算法2、3、4 和算法5，可以判斷CDP 算法在準確率P 和召回率R 方面均有提升，其F1 值高于其他三種算法；但是該算法耗時較多，原因是需要計算文檔數據集的密度。由算法1、2 可知，BERT 模型在處理文本轉向量方面更加優秀。算法1 和算法5 的比較表明，與傳統的K均值文本聚類相比，本文提出的CDP聚類算法有很大的進步。

4.4 實驗結論

結合以上實驗，在文檔數據集上，使用BERT模型對文本進行向量化轉換，極大地提高了文本聚類效果。在此基礎上，本文提出的融合密度和劃分的聚類算法進一步提升了文本聚類效果。實驗表明，本文提出的融合密度和劃分的文本聚類算法與傳統的K 均值文本聚類算法相比，將F1 值提高超10%，效果顯著且穩定。

5 結語

本文使用BERT 中文模型處理文檔向量化，并使用新提出的融合密度和劃分的聚類算法進行文本聚類。與傳統的文本向量化處理相比，BERT 模型在處理文檔向量化方面更為出色；提出融合密度和劃分的文本聚類算法在文檔聚類問題上有著優秀的表現；但該算法也有一些缺點，聚類類別的增加或文檔數量的增加將導致文本聚類的效果略有下降，并且文本聚類將花費較多時間。